《红蓝攻防对抗实战》五.内网探测协议出网之DNS协议探测出网
DNS(Domain Name System)即域名解析系统,可将域名解析到对应访问IP。下面我们还是以系统自带命令为案例,进行演示DNS协议探测出网。
目录
一.Windows系统探测DNS协议出网
二.Linux系统探测DNS协议出网
1. Dig命令
2.Nslookup命令
前文推荐:
- 《红蓝攻防对抗实战》一. 隧道穿透技术详解
- 《红蓝攻防对抗实战》二.内网探测协议出网之TCP/UDP协议探测出网
- 《红蓝攻防对抗实战》三.内网探测协议出网之HTTP/HTTPS协议探测出网
- 《红蓝攻防对抗实战》四.内网探测协议出网之ICMP协议探测出网
一.Windows系统探测DNS协议出网
在Windows系统中测试DNS协议出网可使用Nslookup命令。这是一种网络管理命令行工具,可以用来查询DNS域名和IP解析。nslookup有两种工作模式,交互式和非交互式,这里使用非交互式即可。执行nslookup baidu.com"命令,返回响应结果,证明出网成功,如图1-1所示。
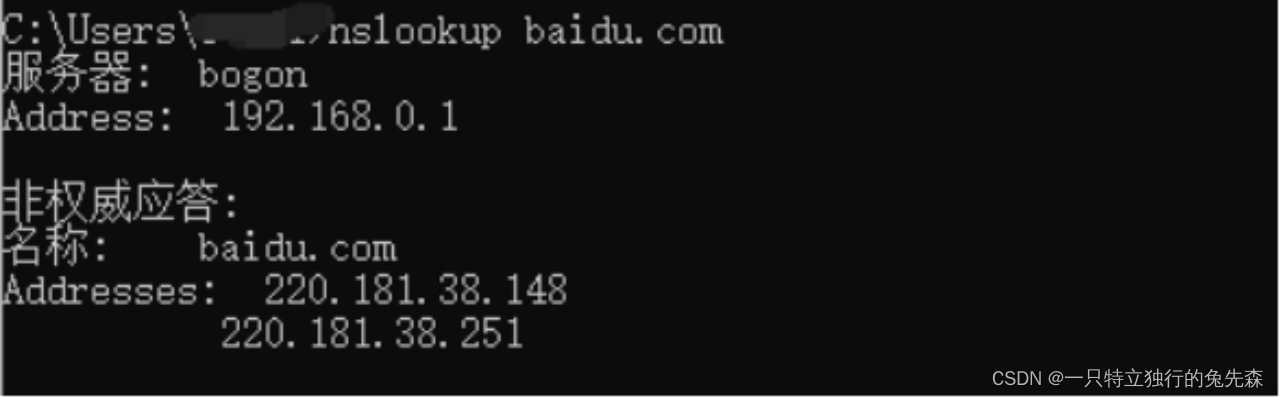
图1-1 Nslookup命令探测出网
二.Linux系统探测DNS协议出网
1. Dig命令
Dig命令在Linux操作系统中用于询问DNS,域名服务器的查询工具可以查询DNS协议下的NS记录、A记录、MX记录相关信息。执行dig @8.8.8.8 www.baidu.com命令,这里指定DNS服务器,8.8.8.8是Google的DNS服务器。返回响应结果,证明出网成功,如图1-2所示。
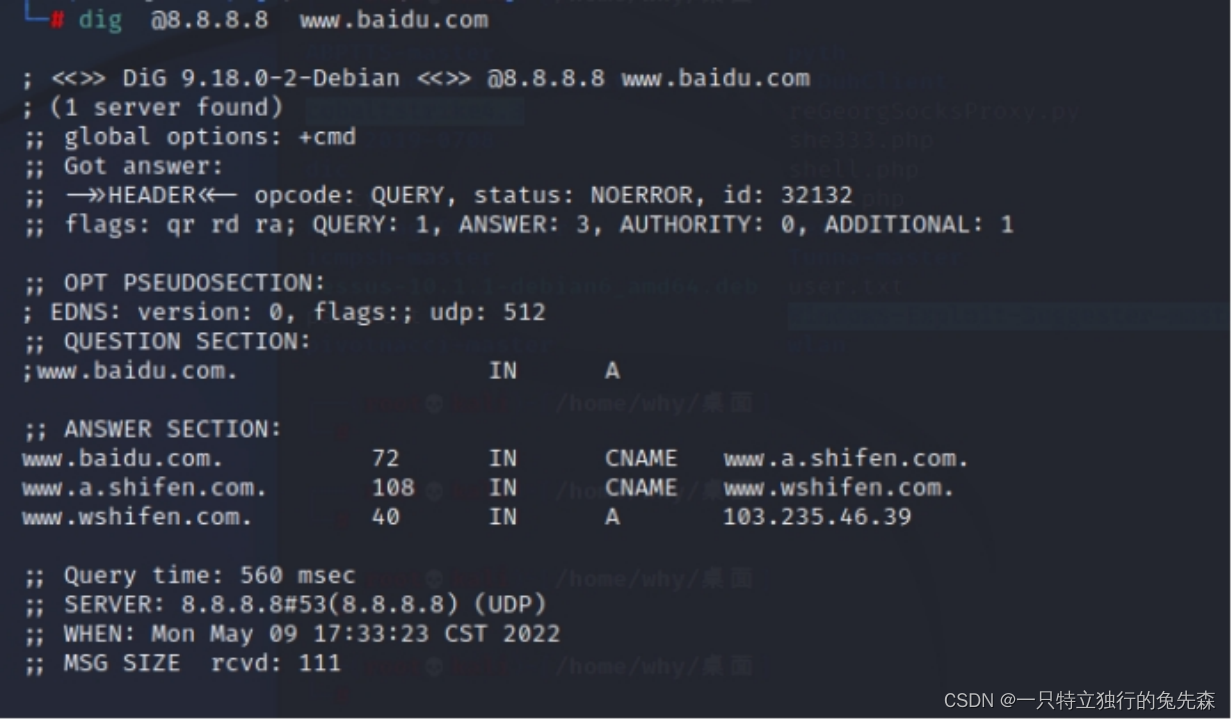
图1-2 Dig命令探测出网成功
2.Nslookup命令
Linux系统中同样也可以使用nslookup命令对系统进行DNS协议探测出网。方法同Windows系统一样,执行nslookup baidu.com命令,执行后通过返回的响应结果证明出网成功,如图1-3所示。
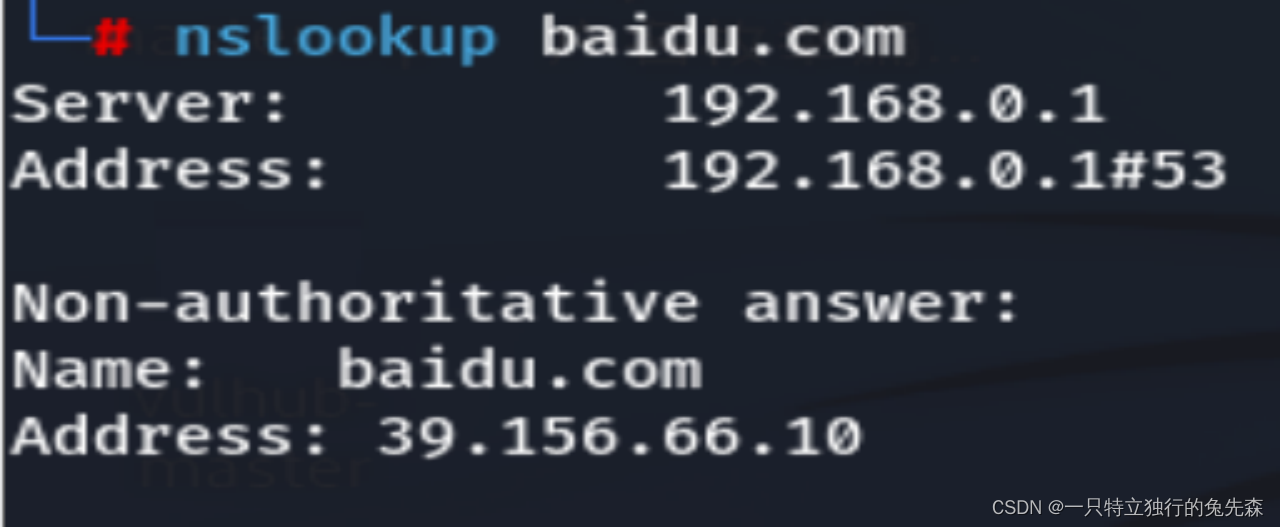
图1-3 nslookup命令探测出网成功
相关文章:

《红蓝攻防对抗实战》五.内网探测协议出网之DNS协议探测出网
DNS(Domain Name System)即域名解析系统,可将域名解析到对应访问IP。下面我们还是以系统自带命令为案例,进行演示DNS协议探测出网。 目录 一.Windows系统探测DNS协议出网 二.Linux系统探测DNS协议出网 1. Dig命令 2.Nslookup命…...

计算机算法分析与设计(18)---回溯法(介绍、子集和问题C++代码)
文章目录 一、回溯法介绍二、子集和问题2.1 知识概述2.2 代码编写 一、回溯法介绍 1. 回溯法(back tracking)是一种选优搜索法,又称为试探法,有“通用的解题法”之称,按选优条件向前搜索,以达到目标。但当探…...
[Hive] explode
在 Hive 中,explode 函数用于将数组(Array)或者Map类型的列拆分成多行, 每个元素或键值对为一行。这允许我们在查询中对数组或 Map 进行扁平化操作。 下面是使用 explode 函数的示例: 假设我们有一个包含数组字段的表…...

2023年10月22日找工作面试交流遇到的基本问题
交叉编译解决的痛点问题 不同硬件体系结构之间的编译问题。嵌入式系统开发需要在主机上编写代码。提高效率和节省时间。软件移植和管理依赖关系。 不同硬件体系结构之间的编译问题:例如,你开发了一个针对Intel x86架构的应用程序,但想要在Ra…...

如何判断要不要用振动技术来进行设备预测性维护
在现代工业设备运行过程中,及时发现设备故障并进行维修对于确保生产线的正常运行至关重要。振动分析技术作为一种先进的设备监测和预测性维护方法,通过实时监测和分析设备的振动信号,可以提前发现潜在故障,降低停机时间和维护成本…...

数据结构和算法——用C语言实现所有树形结构及相关算法
文章目录 前言树和森林基础概念二叉树二叉树的遍历二叉树的构造树和森林与二叉树之间的转化树和森林的遍历 满二叉树完全二叉树线索二叉树线索二叉树的构造寻找前驱和后继线索二叉树的遍历 最优二叉树(哈夫曼树)哈夫曼树的构造哈夫曼编码 二叉排序树&…...
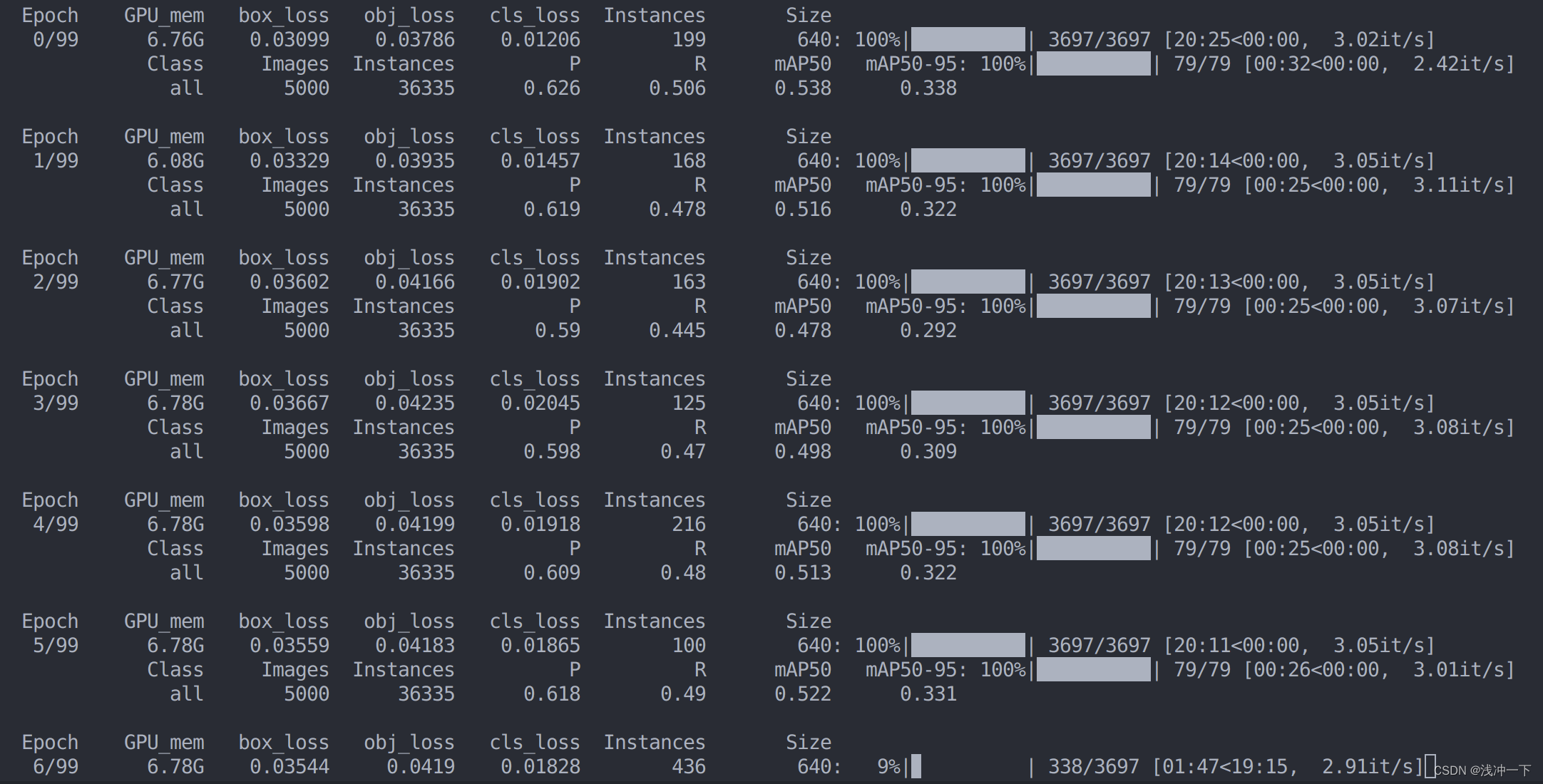
OTA: Optimal Transport Assignment for Object Detection 论文和代码学习
OTA 原因步骤什么是最优传输策略标签分配的OT正标签分配负标签分配损失计算中心点距离保持稳定动态k的选取 整体流程代码使用 论文连接: 原因 1、全部按照一个策略如IOU来分配GT和Anchors不能得到全局最优,可能只能得到局部最优。 2、目前提出的ATSS和P…...
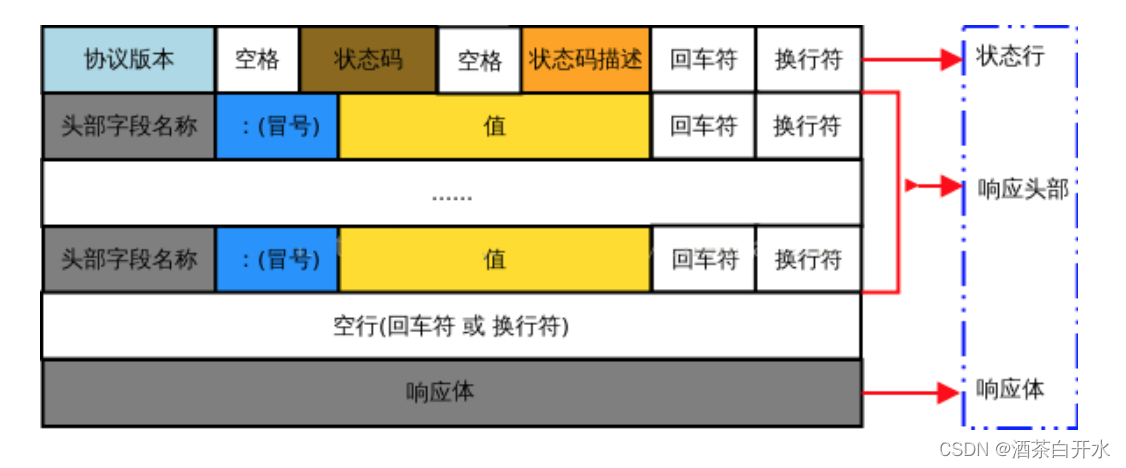
前后端交互—跨域与HTTP
跨域 代码下载 同源策略 同源策略(英文全称 Same origin policy)是浏览器提供的一个安全功能。 MDN 官方给定的概念:同源策略限制了从同一个源加载的文档或脚本如何与来自另一个源的资源进行交互。这 是一个用于隔离潜在恶意文件的重要安全机制。 通俗的理解:浏览器规定&a…...

Error和Exception的关系以及区别
在Java中,Error 和 Exception 是两种不同类型的异常类,它们都继承自 java.lang.Throwable,但在用途和处理方式上有重要区别。 Error: Error 表示在程序运行过程中,通常由于系统或环境的严重问题而引起的异常情况。这些问题通常是无…...

Hive SQL 函数高阶应用场景
HIVE作为数据仓库处理常用工具,如同RDBMS关系型数据库中标准SQL语法一样,Hive SQL也内置了不少系统函数,满足于用户在不同场景下的数据分析需求,以提高开发SQL数据分析的效率。 我们可以使用show functions查看当下版本支持的函数…...

linux下C++开发环境搭建
一.安装GCC,GDB 1.1 先更新软件包安装源 sudo apt update1.2 安装编译器和调试器 sudo apt install build-essential gdb"build-essential" 是编译代码所需要的工具。 "gdb" 是调试器。1. build-essential:- "build-essential" 是一个用于Ubu…...

报错问题解决办法:Decryption error sun.security.rsa.RSAPadding.unpadV15
报错问题解决办法:Decryption error sun.security.rsa.RSAPadding.unpadV15 出现的问题 javax.crypto.BadPaddingException: Decryption errorat sun.security.rsa.RSAPadding.unpadV15(RSAPadding.java:380) ~[na:1.8.0_131]at sun.security.rsa.RSAPadding.unpa…...

LVS+DR部署
LVS-DR的工作原理: 1.客户端会发送请求到vip 2.LVS的调度器接受请求之后,根据算法选择一台真实服务器,请求转发到后端RS,请求的报文的目的MAC地址,修改成后端真实服务器的MAC地址,转发。 3.后端真实服务器…...

C++项目——云备份-②-第三方库认识
文章目录 专栏导读1. json 认识1.1 JSON 数据结构的特点 2. jsoncpp库认识3. json实现序列化案例4. json实现反序列化案例5. bundle文件压缩库认识6. bundle库实现文件压缩案例7.bundle库实现文件解压缩案例8.httplib库认识9. httplib库搭建简单服务器案例10. httplib库搭建简单…...

Linux入门攻坚——4、shell编程初步、grep及正则表达式
bash的基础特性(续): 1、提供了编程环境: 编程风格:过程式:以指令为中心,数据服务于执行;对象式:以数据为中心,指令服务于数据 shell编程,编译执…...
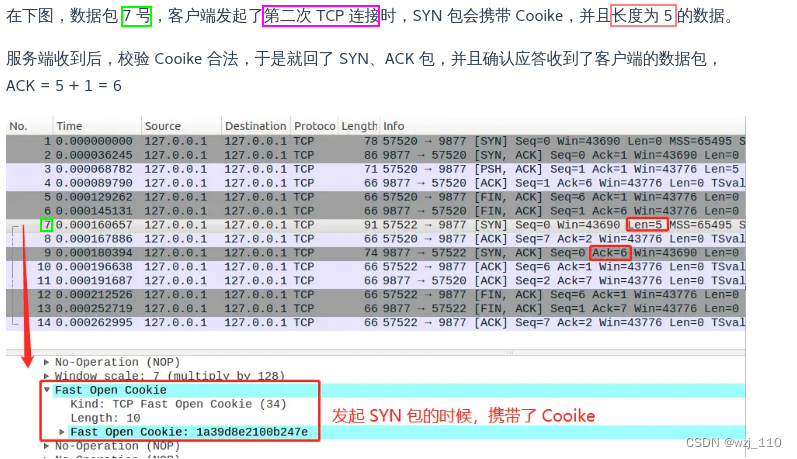
TCP/IP(二十二)TCP 实战抓包分析(六)TCP 快速建立连接
一 TCP Fast Open 快速建立连接 说明: 之前讲解TCP 相关知识点遗漏了这个知识点,补充上 ① TFO简介 ② 请求 Fast Open Cookie过程 "原理图" ③ 真正开始 TCP Fast Open 重点: TFO 使 SYN包 可以包含payload 数据 ④ 抓包分析 1、…...
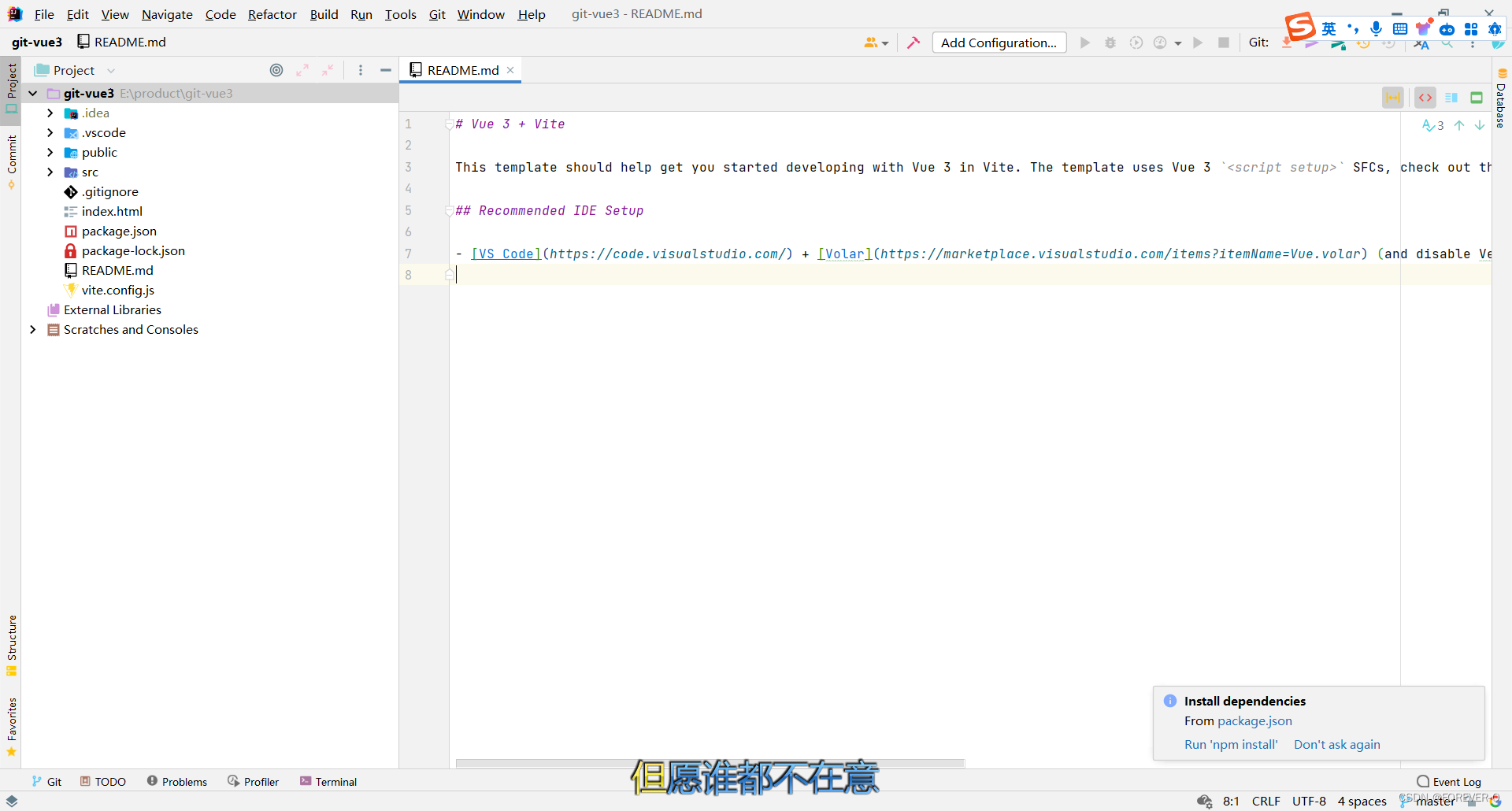
IDEA如何拉取gitee项目?
1.登录gitee 说明:打开idea,在设置上面搜索框输入gitee,然后登录gitee注册的账号。 2. 创建gitee仓库 说明:创建idea中的gitee仓库。 3.寻找项目文件 说明:为需要添加gitee仓库的项目进行添加。 4.项目右键 说明&a…...
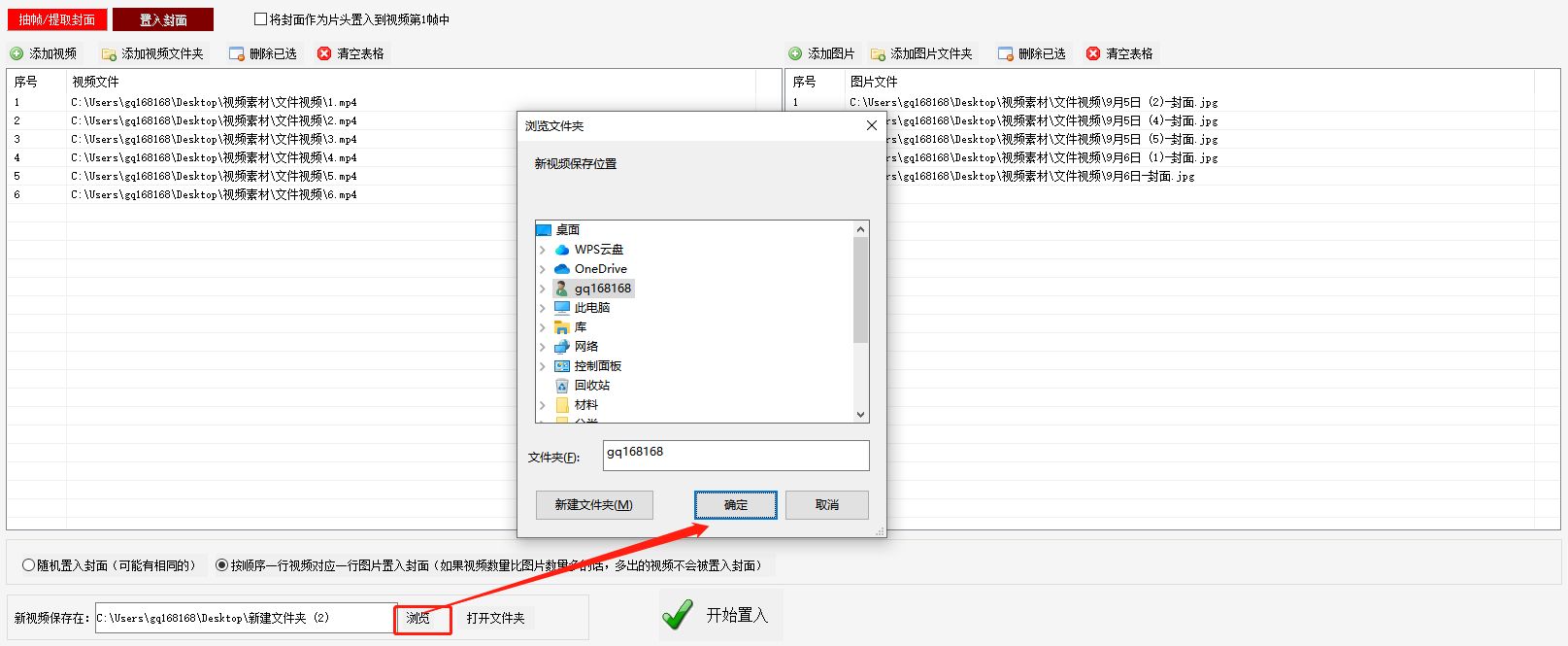
视频编辑不求人,教你一招制胜批量添加封面
视频添加封面是一个相当简单的任务,您只需要一款专门的软件,就能轻松搞定!下面就是详细教程啦! 首先,您需要在浏览器中搜索“固乔智剪软件”,进入官网并下载这款软件。固乔智剪软件是一款非常专业的视频剪辑…...

产品的竞争力是什么
产品的竞争力归根到底是3点:功能,性能,容量。 功能 我这个产品完成了别人没有实现的功能,而且是用户需要的。解决了客户的痛点 性能 我这个产品的功能虽然别人有,但是我性能好,性能好意味着干同样的活给…...

vue3 拖拽插件 Vue3DraggableResizable
Vue3DraggableResizable 拖拽插件的官方文档 一、Vue3DraggableResizable 的属性和事件 1、Vue3DraggableResizable 的属性配置 属性类型默认值功能描述示例initWNumbernull设置初始宽度(px)<Vue3DraggableResizable :initW“100” />initHNumb…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
