C语言文件操作(1)
C语言文件操作(1)
文章目录
- C语言文件操作(1)
- 一、理解文件
- 1.概述
- 2.分类
- ①.正常角度
- ②.文本文件和二进制文件
- 二、文件的打开和关闭
- 1.流和标准流
- 2.文件类型指针
- 3.文件的打开和关闭以及使用类型
- 三、文件缓冲区
一、理解文件
1.概述
首先,我们要知道文件都是存储在磁盘上的,而我们平时写在编译器上写的代码等在保存之前都是存储在内存中的,也即带电存储,计算机内存是一种临时存储器,它的内容在计算机关闭或重启时会被清除,或者程序退出,内存回收,数据就丢失了。
如果想要永久化的保存数据,我们可以使用存储在磁盘上的文件。
2.分类
①.正常角度
从程序设计的角度来看,文件主要分为程序文件和数据文件。程序文件也就是我们常说的.c .obj .exe文件。
而在编程过程中的文件操作主要操作的就是数据文件,程序运行时读取数据的文件和程序运行时输出内容的文件。
注意:
程序中的数据 ———> 磁盘中的文件,这叫输出,即写
程序中的数据 <——— 磁盘中的文件,这叫输入,即读
输出输入是相对于程序中的数据来说的。
②.文本文件和二进制文件
根据数据的存储形式,数据文件被称为文本文件或者二进制文件。
数据在内存中以⼆进制的形式存储,如果不加转换的输出到外存,就是二进制文件。
如果要求在外存上以ASCII码的形式存储,则需要在存储前转换。以ASCII字符的形式存储的文件就是文本文件。
在内存中,字符⼀律以ASCII形式存储,数值型数据既可以用ASCII形式存储,也可以使用⼆进制形式存储。
举个例子:
将100以二进制形式写到文件里,出现不认识的函数大家不用担心,后续都会提到的呀!
#include <errno.h>
int main()
{int a = 100;FILE* fp = fopen("test.txt", "wb");if (fp == NULL){perror("fopen");return 1;}fwrite(&a, 4, 1, fp);fclose(fp);fp = NULL;return 0;
}
那让我们一起来验证一下:
1.将这个文件拖到源文件下面
2.右键点击打开方式选项
3.选择二进制编辑器
二、文件的打开和关闭
1.流和标准流
我们程序的数据需要输出到各种外部设备,也需要从外部设备获取数据,不同的外部设备的输入输出操作各不相同,为了方便程序员对各种设备进行方便的操作,我们抽象出了流的概念,我们可以把流想象成流淌着字符的河。
C程序针对文件、画面、键盘等的数据输入输出操作都是同流操作的。一般情况下,我们要想向流里写数据,或者从流中读取数据,都是要打开流,然后操作。
那为什么我们从键盘输入数据,向屏幕上输出数据,并没有打开流呢?
那是因为C语言程序在启动的时候,默认打开了3个流:
stdin - 标准输入流,在大多数的环境中从键盘输入。
stdout - 标准输出流,在大多数的环境中输出至显示器界面。
stderr - 标准错误流,在大多数环境中输出到显示器界面。
这是默认打开了这三个流,我们使scanf、printf等函数就可以直接进行输入输出操作的。
2.文件类型指针
在使用文件,打开文件时,文件都会在内存中创建一个“文件信息区”,存放文件的相关信息,这些信息都保存在一个结构体变量里,FILE是这个结构体类型,创建一个FILE*类型的指针,可以指向这个文件信息区,并且通过文件信息来访问这个文件,通过文件指针变量能够间接找到这个与他关联的文件。
stdin、stdout、stderr三个流的类型是: FILE* ,通常称为文件指针。C语言中,就是通过 FILE* 的文件指针来维护流的各种操作的。
3.文件的打开和关闭以及使用类型
文件的打开和关闭,是依赖与fopen函数和fclose函数
//文件的打开
FILE* fp = fopen("test.txt", "wb");//注意:文件名和打开模式都是两个双引号if (fp == NULL){perror("fopen");return 1;}
//文件的关闭fclose(fp);fp = NULL;
fopen打开成功返回文件信息区的地址,打开失败返回NULL。
FILE * fopen ( const char * filename, const char * mode );
下面让我们一起来看看mode,也就是文件的打开模式
首先,我们来看一下"r"和"w"
r:文件必须存在,不存在的话则打开失败
w:如果文件存在会清空原来内容,相当于变成空文件,如果不存在,则创建一个新的文件。
更多有关mode的类型,可以点开这个链接。
fopen的mode
三、文件缓冲区
ANSIC 标准采用“缓冲文件系统”处理的数据文件的,所谓缓冲文件系统是指系统自动地在内存中为程序中每⼀个正在使用的文件开辟⼀块“文件缓冲区”。从内存向磁盘输出数据会先送到内存中的缓冲区,装满缓冲区后才一起送到磁盘上。如果从磁盘向计算机读入数据,则从磁盘文件中读取数据输入到内存缓冲区(充满缓冲区),然后再从缓冲区逐个地将数据送到程序数据区(程序变量等)。缓冲区的大小根据C编译系统决定的。
int main()
{FILE* pf = fopen("test.txt", "w");fputs("abcdef", pf);//先将代码放在输出缓冲区printf("睡眠10秒-已经写数据了,打开test.txt文件,发现文件没有内容\n");Sleep(10000);printf("刷新缓冲区\n");fflush(pf);//刷新缓冲区时,才将输出缓冲区的数据写到文件(磁盘)//注:fflush 在高版本的VS上不能使用了printf("再睡眠10秒-此时,再次打开test.tx文件,文件有内容了\n");Sleep(10000);//避免是fclose的影响fclose(pf);//注:fclose在关闭文件的时候,也会刷新缓冲区pf = NULL;return 0;
}
因为有缓冲区的存在,C语言在操作文件的时候,需要做刷新缓冲区或者在文件操作结束的时候关闭文件。
相关文章:

C语言文件操作(1)
C语言文件操作(1) 文章目录 C语言文件操作(1)一、理解文件1.概述2.分类①.正常角度②.文本文件和二进制文件 二、文件的打开和关闭1.流和标准流2.文件类型指针3.文件的打开和关闭以及使用类型 三、文件缓冲区 一、理解文件 1.概述…...
)
adb 操作命令(adb调试QT项目使用到的命令)
1.adb连接串口 获取root权限 adb root && adb remount && adb shell2.测试串口命令 stty -F /dev/ttyS4 cs8 -parenb -cstopb -echoecho "12345\n" > /dev/ttyS8cat /dev/ttyS4 &3.软件在安卓系统上的名字已经活动名称(下面是示…...
mysql下载和安装,使用
先下载安装 官方下载 已下载备份软件 安装,一路下一步设置环境变量 4. 打开一个cmd,输入mysql -u root -p...
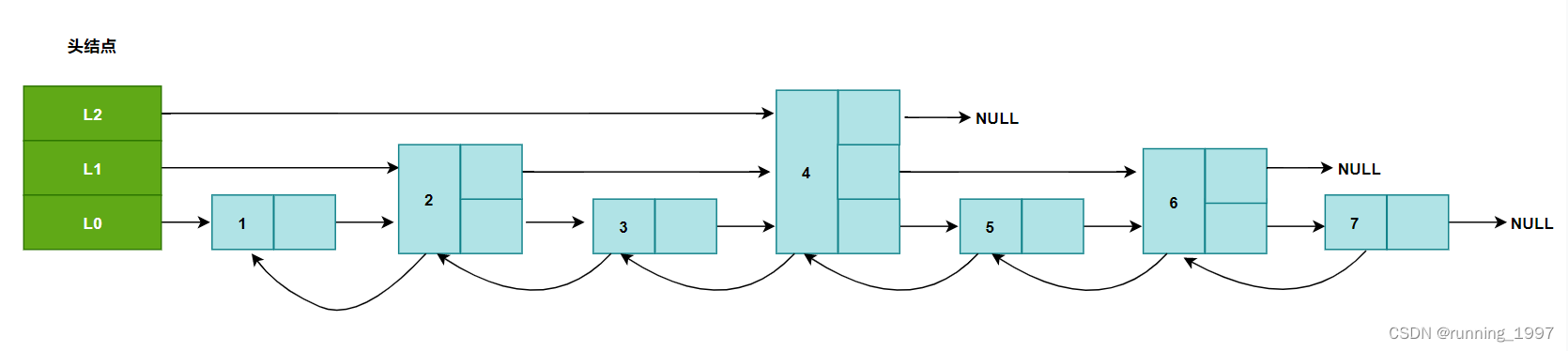
Redis底层核心数据结构详解
文章目录 一、深入String(SDS)1. 字符串简介2. SDS存在的意义3. SDS结构设计4. SDS与C字符串的区别4.1 常数复杂度获取字符串长度4.2 杜绝缓冲区溢出4.3 二进制安全4.4 SDS API 5 小结 二、深入List (QuickList)1. 链表节点结构设计2. Redis的链表实现的…...

如何学会从产品经理角度去思考问题?
如何学会从产品经理角度去思考问题? 从产品经理的角度思考问题意味着你需要关注产品从构思到上市全过程中的各个方面,包括用户需求、市场趋势、设计、开发、测试、上市后的用户反馈等。以下是一些策略和方法,帮助你培养从产品经理角度思考问…...

正则表达式的神奇世界:表达、匹配和提取
正则表达式的神奇世界:表达、匹配和提取 前言第一: 什么是正则表达式?第二: 字符匹配和量词:1. 字符匹配:2. 量词:3. 贪婪和非贪婪匹配: 第三:字符类和元字符1. 字符类&a…...

密码登录虽安全,但有时很麻烦!如何禁用或删除Windows 11中的密码登录
如果你想在Windows 11上自动登录,在本指南中,我们将向你展示如何删除你的帐户密码。 在Windows 11上,你可以至少通过三种方式从帐户中删除登录密码。在你的帐户上使用密码有助于保护你的计算机和文件免受来自internet或本地的未经授权的访问。然而,在某些情况下,密码可能…...

Python实现的快速排序代码
Python实现的快速排序代码 def bubble_sort(arr): n len(arr) for i in range(n): for j in range(0, n-i-1): if arr[j] > arr[j1]: arr[j], arr[j1] arr[j1], arr[j] return arr 冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,…...

【USRP】通信基带物理层历史
无线通信的基带物理层开发历史涵盖了从早期无线技术到当前复杂的移动通信标准的各种进步。以下是关于无线通信基带物理层开发的简要历史概述: 无线电初期:20世纪初,Guglielmo Marconi等人通过无线电进行了早期的无线通信尝试。这些早期的尝试…...
依靠继承与聚合,实现maven搭建分布式项目
简介聚合 对于复杂的Maven项目,一般建议采用多模块的方式来设计开发,便于后期维护管理。但是构建项目时,如果每次都需要按模块一个一个进行构建会十分麻烦,而Maven的聚合功能就可以很好的解决这个问题,当用户对聚合模…...
【java】A卷+B卷)
华为OD 叠积木(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

vue重修之自定义项目、ESLint和代码规范修复
文章目录 VueCli 自定义创建项目ESlint代码规范及手动修复代码规范错误 VueCli 自定义创建项目 安装脚手架 (已安装) npm i vue/cli -g创建项目 vue create xxx选项 Vue CLI v5.0.8 ? Please pick a preset:Default ([Vue 3] babel, eslint)Default ([Vue 2] babel, eslint) …...
【java】A卷+B卷)
华为OD 完全二叉树非叶子部分后序遍历(200分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应往年部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为OD…...

AI是未来?——神经网络篇
AI是未来?——神经网络篇 文章目录 AI是未来?——神经网络篇1. 神经网络小记问题记录: 1. 神经网络小记 疑问:假如让神经网络识别一张猫的图片,他经过了n个神经元节点最终识别为了狗。那么此时观察产生反应的这些神经…...

c语言练习94:分割链表
分割链表 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你不需要 保留 每个分区中各节点的初始相对位置。 示例 1: 输入:head [1,4,3,2,5,2], x…...
【java】A卷+B卷)
华为OD 数组二叉树(200分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应往年部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为OD…...
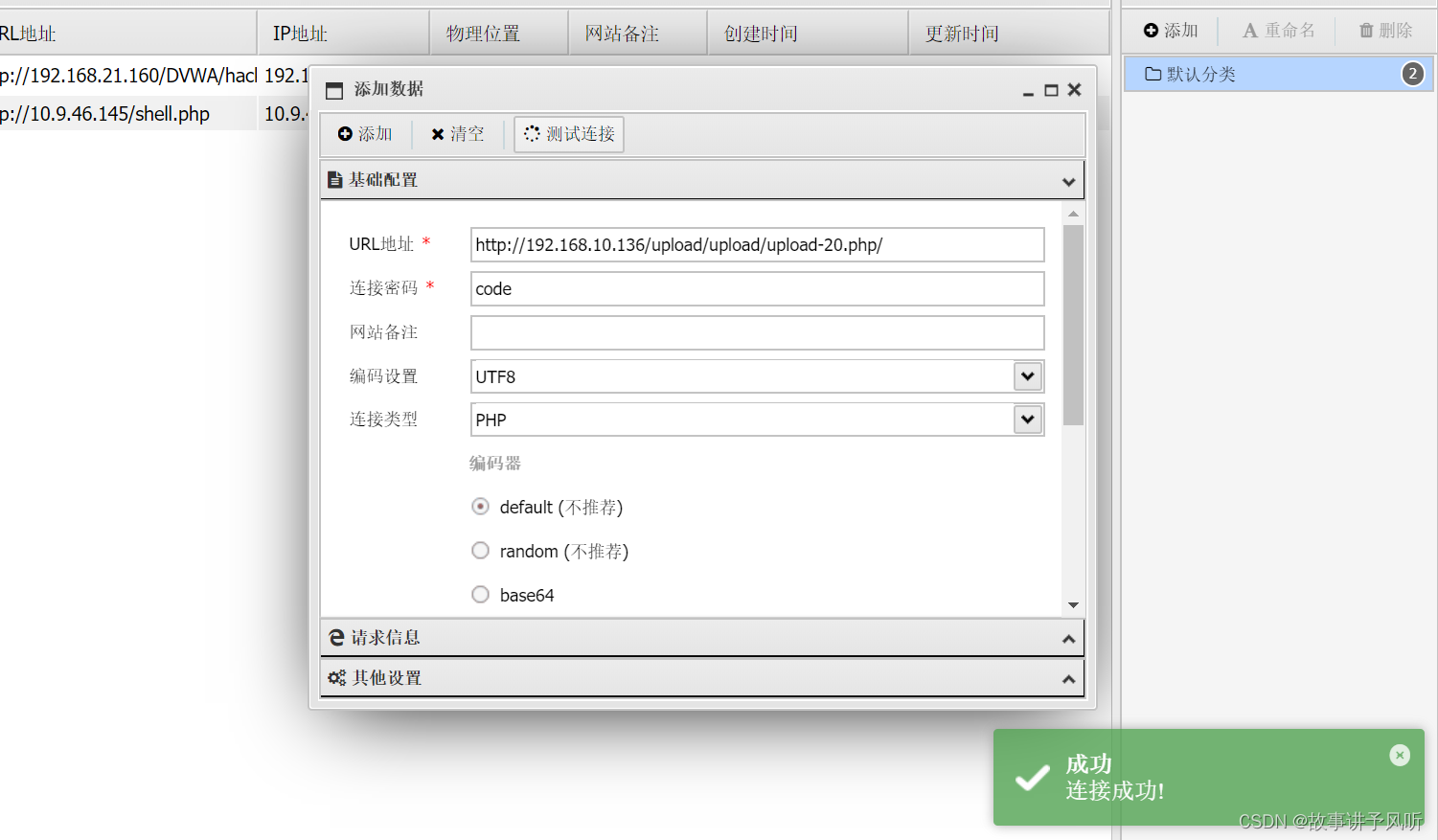
Upload-labs(1-20关保姆级教程)
靶场下载链接 https://github.com/c0ny1/upload-labs 话不多说,直接喂饭 lab-1 上传php木马,发现弹出提示框,查看源码可知是前端过滤 bp抓包,先上传一张正常的jpg图片 修改文件内容和后缀,大概就是想怎么改就怎么…...
C语言实现调整数组中奇数偶数顺序
目录 1.思路2. 代码 1.思路 给定两个下标left和right,left放在数组的起始位置,right放在数组中最后一个元素的位置循环进行一下操作 a. 如果left和right表示的区间[left, right]有效,进行b,否则结束循环 b. left从前往后找&#…...

从车窗升降一探 Android 车机的重要 API:车辆属性 CarProperty
前言 前面我们介绍过 Android 车机 Automotive OS 的几块重要内容: 一文了解 Android 车机如何处理中控的旋钮输入从实体按键看 Android 车机的自定义事件机制深度入门 Android 车机核心 CarService 的构成和链路 本篇文章我们聚焦 Android 车机上最重要、最常用…...
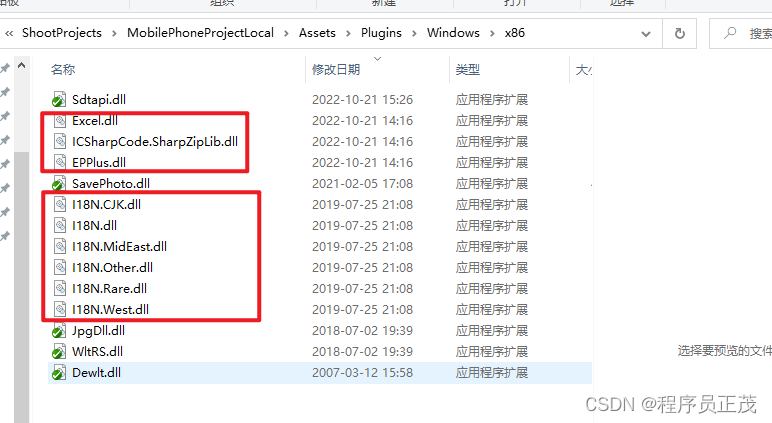
Unity读取写入Excel
1.在Plugins中放入dll,118开头的dll在Unity安装目录下(C:\Program Files\Unity\Editor\Data\Mono\lib\mono\unity) 2.写Excel public void WriteExcel(){//文件地址FileInfo newFile new FileInfo(Application.dataPath "/test.xlsx…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...

宠物车载安全座椅市场报告:解读行业趋势与投资前景
一、什么是宠物车载安全座椅? 宠物车载安全座椅是一种专为宠物设计的车内固定装置,旨在保障宠物在乘车过程中的安全性与舒适性。它通常由高强度材料制成,具备良好的缓冲性能,并可通过安全带或ISOFIX接口固定于车内。 近年来&…...
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...
