python数据结构和算法(1)
数据结构和算法简介
数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。
算法:解决问题的思维、步骤和方法。
程序 = 数据结构 + 算法
算法
算法的独立性
算法是独立存在的一种解决问题的方法和思想,对于算法而言,实现的语言并不重要,重要的是思想,算法可以有不同的语言描述实现版本
算法的特点
- 有输入:算法具有0个或者多个输入
- 有输出:算法至少有1个或者多个输出
- 有穷性:算法在有限的步骤之后会自动结束而不会无限循环,并且每一个步骤可以在可接受的时间内完成
- 确定性:算法中的每一步都有确定的含义,不会出现二义性
- 可行性:算法的每一步都是可行的,即每一步都能够执行有限的次数完成
算法对比
对于同一个问题,我们给出了两种解决算法,在两种算法的实现中,我们对程序的执行时间进行了测算,发现两段程序执行的时间相差悬殊,由此我们可以得出结论:实现算法程序的执行时间可以反映出算法的效率
但是,单靠时间值衡量算法效率并不可靠
假设计算机执行算法每一个基本操作的时间是固定的一个时间单位,那么有多少个基本操作就代表花费多少时间单位,由此可以忽略机器环境的影响而客观的反应算法的时间效率
. 代码执行总时间 ( T ) = 操作步骤数量 ∗ 操作步骤执行时间 .代码执行总时间(T) = 操作步骤数量 * 操作步骤执行时间 .代码执行总时间(T)=操作步骤数量∗操作步骤执行时间
时间复杂度
时间复杂度表示一个苏娜发随着问题规模不断变化的最主要趋势,通常用来衡量一个算法的优劣
时间复杂度的表示形式
大O 记法 为算法的时间复杂度随数据量变化的关系曲线,通常由最高次项决定,当数据量比较高时低次项的影响相对于高次项就很小,为了方便可以忽略
时间复杂度的计算规则
- 基本操作 时间复杂度为
O(1) - 顺序结构 时间复杂度按加法计算
- 循环结构 时间复杂度按乘法计算
- 分支结构 时间复杂度取最大值
- 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其他次要项和常数项可以忽略
- 在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
最优最坏时间复杂度
分析算法时,存在集中可能的考虑
- 算法完成工作最少需要多少基本操作,即 最优时间复杂度
- 算法完成工作最多需要多少基本操作,即 最坏时间复杂度
- 算法完成工作平均需要多少基本操作,即 平均时间复杂度
最优最坏时间复杂度的作用
- 最优时间复杂度:反映的知识最乐观最理想的情况,没有参考价值
- 最坏时间复杂度:算法的一种保证,表示算法在此种程度的基本操作中一定能完成工作
- 平均时间复杂度:是对苏娜发的一个全面评价,因此它完整全面的反映了这个算法的性质,但另一方面,这种平衡并没有保证,不是每个计算都能在这个基本操作内完成。而且,对于平均情况的计算,也会因为应用苏娜发的实例分布可能并不均匀而难以计算。
我们主要关注算法的最坏情况,即最坏时间复杂度
常见的时间复杂度
- O ( 1 ) O(1) O(1) 常数阶
- O ( l o g n ) O(logn) O(logn) 对数阶
- O ( n ) O(n) O(n) 线数阶
- O ( n 2 ) O(n^2) O(n2) 平方阶
- O ( n 3 ) O(n^3) O(n3) 立方阶
效率高到低分别是
O ( 1 ) > O ( l o g n ) > O ( n ) > O ( n ∗ l o g n ) > O ( n 2 ) > O ( n 3 ) O(1) > O(logn) > O(n) >O(n * logn) > O(n^2) > O(n^3) O(1)>O(logn)>O(n)>O(n∗logn)>O(n2)>O(n3)
空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的度量,类似于时间复杂度。一个算法的空间复杂度 S ( n ) S(n) S(n) 定义为该算法所耗费的存储空间
相关文章:
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...

视觉slam--框架
视觉里程计的框架 传感器 VO--front end VO的缺点 后端--back end 后端对什么数据进行优化 利用什么数据进行优化的 后端是怎么进行优化的 回环检测 建图 建图是指构建地图的过程。 构建的地图是点云地图还是什么信息的地图? 建图并没有一个固定的形式和算法…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...

npm install 相关命令
npm install 相关命令 基本安装命令 # 安装 package.json 中列出的所有依赖 npm install npm i # 简写形式# 安装特定包 npm install <package-name># 安装特定版本 npm install <package-name><version>依赖类型选项 # 安装为生产依赖(默认&…...
)
Spring Boot 与 Kafka 的深度集成实践(二)
3. 生产者实现 3.1 生产者配置 在 Spring Boot 项目中,配置 Kafka 生产者主要是配置生产者工厂(ProducerFactory)和 KafkaTemplate 。生产者工厂负责创建 Kafka 生产者实例,而 KafkaTemplate 则是用于发送消息的核心组件&#x…...

【学习记录】使用 Kali Linux 与 Hashcat 进行 WiFi 安全分析:合法的安全测试指南
文章目录 📌 前言🧰 一、前期准备✅ 安装 Kali Linux✅ 获取支持监听模式的无线网卡 🛠 二、使用 Kali Linux 进行 WiFi 安全测试步骤 1:插入无线网卡并确认识别步骤 2:开启监听模式步骤 3:扫描附近的 WiFi…...
)
后端下载限速(redis记录实时并发,bucket4j动态限速)
✅ 使用 Redis 记录 所有用户的实时并发下载数✅ 使用 Bucket4j 实现 全局下载速率限制(动态)✅ 支持 动态调整限速策略✅ 下载接口安全、稳定、可监控 🧩 整体架构概览 模块功能Redis存储全局并发数和带宽令牌桶状态Bucket4j Redis分布式限…...

vue3 手动封装城市三级联动
要做的功能 示意图是这样的,因为后端给的数据结构 不足以使用ant-design组件 的联动查询组件 所以只能自己分装 组件 当然 这个数据后端给的不一样的情况下 可能组件内对应的 逻辑方式就不一样 毕竟是 三个 数组 省份 城市 区域 我直接粘贴组件代码了 <temp…...

Angular中Webpack与ngx-build-plus 浅学
Webpack 在 Angular 中的概念 Webpack 是一个模块打包工具,用于将多个模块和资源打包成一个或多个文件。在 Angular 项目中,Webpack 负责将 TypeScript、HTML、CSS 等文件打包成浏览器可以理解的 JavaScript 文件。Angular CLI 默认使用 Webpack 进行项目…...

大模型智能体核心技术:CoT与ReAct深度解析
**导读:**在当今AI技术快速发展的背景下,大模型的推理能力和可解释性成为业界关注的焦点。本文深入解析了两项核心技术:CoT(思维链)和ReAct(推理与行动),这两种方法正在重新定义大模…...

信息系统分析与设计复习
2024试卷 单选题(20) 1、在一个聊天系统(类似ChatGPT)中,属于控制类的是()。 A. 话语者类 B.聊天文字输入界面类 C. 聊天主题辨别类 D. 聊天历史类 解析 B-C-E备选架构中分析类分为边界类、控制类和实体类。 边界…...

Linux【5】-----编译和烧写Linux系统镜像(RK3568)
参考:讯为 1、文件系统 不同的文件系统组成了:debian、ubuntu、buildroot、qt等系统 每个文件系统的uboot和kernel是一样的 2、源码目录介绍 目录 3、正式编译 编译脚本build.sh 帮助内容如下: Available options: uboot …...

记一次spark在docker本地启动报错
1,背景 在docker中部署spark服务和调用spark服务的微服务,微服务之间通过fegin调用 2,问题,docker容器中服务器来后,注册中心都有,调用服务也正常,但是调用spark启动任务后报错,报错…...

【向量库】Weaviate 搜索与索引技术:从基础概念到性能优化
文章目录 零、概述一、搜索技术分类1. 向量搜索:捕捉语义的智能检索2. 关键字搜索:精确匹配的传统方案3. 混合搜索:语义与精确的双重保障 二、向量检索技术分类1. HNSW索引:大规模数据的高效引擎2. Flat索引:小规模数据…...

ABB馈线保护 REJ601 BD446NN1XG
配电网基本量程数字继电器 REJ601是一种专用馈线保护继电器,用于保护一次和二次配电网络中的公用事业和工业电力系统。该继电器在一个单元中提供了保护和监控功能的优化组合,具有同类产品中最佳的性能和可用性。 REJ601是一种专用馈线保护继电器…...

Heygem50系显卡合成的视频声音杂音模糊解决方案
如果你在使用50系显卡有杂音的情况,可能还是官方适配问题,可以使用以下方案进行解决: 方案一:剪映替换音色(简单适合普通玩家) 使用剪映换音色即可,口型还是对上的,没有剪映vip的&…...

Gitlab + Jenkins 实现 CICD
CICD 是持续集成(Continuous Integration, CI)和持续交付/部署(Continuous Delivery/Deployment, CD)的缩写,是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后,自动发布…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...
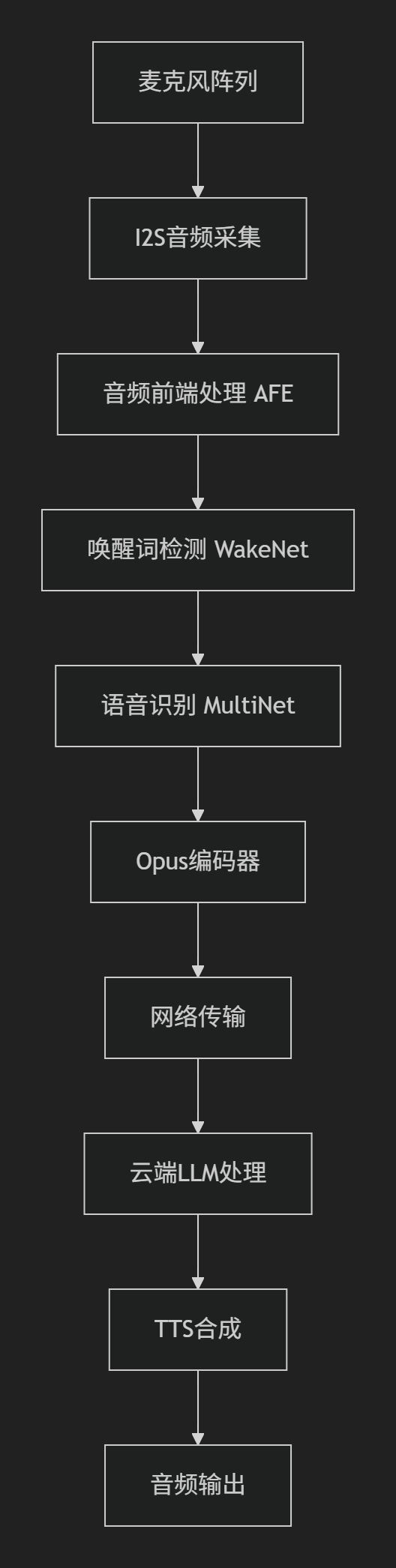
SDU棋界精灵——硬件程序ESP32实现opus编码
一、 音频处理框架 该项目基于Espressif的音频处理框架构建,核心组件包括 ESP-ADF 和 ESP-SR,以下是完整的音频处理框架实现细节: 1.核心组件 (1) 音频前端处理 (AFE - Audio Front-End) main/components/audio_pipeline/afe_processor.c功能: 声学回声…...

Spring AI中使用ChatMemory实现会话记忆功能
文章目录 1、需求2、ChatMemory中消息的存储位置3、实现步骤1、引入依赖2、配置Spring AI3、配置chatmemory4、java层传递conversaionId 4、验证5、完整代码6、参考文档 1、需求 我们知道大型语言模型 (LLM) 是无状态的,这就意味着他们不会保…...

Qt 按钮类控件(Push Button 与 Radio Button)(1)
文章目录 Push Button前提概要API接口给按钮添加图标给按钮添加快捷键 Radio ButtonAPI接口性别选择 Push Button(鼠标点击不放连续移动快捷键) Radio Button Push Button 前提概要 1. 之前文章中所提到的各种跟QWidget有关的各种属性/函数/方法&#…...
生成对抗网络(GAN)损失函数解读
GAN损失函数的形式: 以下是对每个部分的解读: 1. , :这个部分表示生成器(Generator)G的目标是最小化损失函数。 :判别器(Discriminator)D的目标是最大化损失函数。 GAN的训…...

汇编语言学习(三)——DoxBox中debug的使用
目录 一、安装DoxBox,并下载汇编工具(MASM文件) 二、debug是什么 三、debug中的命令 一、安装DoxBox,并下载汇编工具(MASM文件) 链接: https://pan.baidu.com/s/1IbyJj-JIkl_oMOJmkKiaGQ?pw…...
和向下转型(Downcasting))
【Java基础】向上转型(Upcasting)和向下转型(Downcasting)
在面向对象编程中,转型(Casting) 是指改变对象的引用类型,主要涉及 继承关系 和 多态。 向上转型(Upcasting) ⬆️ 定义 将 子类对象 赋值给 父类引用(自动完成,无需强制转换&…...
)
GitHub 常见高频问题与解决方案(实用手册)
1.Push 提示权限错误(Permission denied) 问题: Bash Permission denied (publickey) fatal: Could not read from remote repository. 原因: 没有配置 SSH key 或使用了 HTTPS 而没有权限…...
数据可视化交互
目录 【实验目的】 【实验原理】 【实验环境】 【实验步骤】 一、安装 pyecharts 二、下载数据 三、实验任务 实验 1:AQI 横向对比条形图 代码说明: 运行结果: 实验 2:AQI 等级分布饼图 实验 3:多城市 AQI…...

安宝特方案丨从依赖经验到数据驱动:AR套件重构特种装备装配与质检全流程
在高压电气装备、军工装备、石油测井仪器装备、计算存储服务器和机柜、核磁医疗装备、大型发动机组等特种装备生产型企业,其产品具有“小批量、多品种、人工装配、价值高”的特点。 生产管理中存在传统SOP文件内容缺失、SOP更新不及、装配严重依赖个人经验、产品装…...
【JavaEE】万字详解HTTP协议
HTTP是什么?-----互联网的“快递小哥” 想象我们正在网上购物:打开淘宝APP,搜索“蓝牙耳机”,点击商品图片,然后下单付款。这一系列操作背后,其实有一个看不见的“快递小哥”在帮我们传递信息,…...
)
Vue3学习(接口,泛型,自定义类型,v-for,props)
一,前言 继续学习 二,TS接口泛型自定义类型 1.接口 TypeScript 接口(Interface)是一种定义对象形状的强大工具,它可以描述对象必须包含的属性、方法和它们的类型。接口不会被编译成 JavaScript 代码,仅…...

华为云Flexus+DeepSeek征文 | MaaS平台避坑指南:DeepSeek商用服务开通与成本控制
作者简介 我是摘星,一名专注于云计算和AI技术的开发者。本次通过华为云MaaS平台体验DeepSeek系列模型,将实际使用经验分享给大家,希望能帮助开发者快速掌握华为云AI服务的核心能力。 目录 作者简介 前言 一、技术架构概览 1.1 整体架构设…...
