【Leetcode】【中等】1726.同积元组
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。![]() https://leetcode.cn/problems/tuple-with-same-product/
https://leetcode.cn/problems/tuple-with-same-product/
给你一个由 不同 正整数组成的数组 nums ,请你返回满足 a * b = c * d 的元组 (a, b, c, d) 的数量。其中 a、b、c 和 d 都是 nums 中的元素,且 a != b != c != d 。
示例 1:
输入:nums = [2,3,4,6] 输出:8 解释:存在 8 个满足题意的元组: (2,6,3,4) , (2,6,4,3) , (6,2,3,4) , (6,2,4,3) (3,4,2,6) , (4,3,2,6) , (3,4,6,2) , (4,3,6,2)
示例 2:
输入:nums = [1,2,4,5,10] 输出:16 解释:存在 16 个满足题意的元组: (1,10,2,5) , (1,10,5,2) , (10,1,2,5) , (10,1,5,2) (2,5,1,10) , (2,5,10,1) , (5,2,1,10) , (5,2,10,1) (2,10,4,5) , (2,10,5,4) , (10,2,4,5) , (10,2,5,4) (4,5,2,10) , (4,5,10,2) , (5,4,2,10) , (5,4,10,2)
自己的思路
一开始真的去定义了一个四元组,做完超时了,后面改成HashMap,这里把四元组的代码贴出来,当做复习了。。。
public static class FourTuple<Object> {public Object first;public Object second;public Object third;public Object fourth;public FourTuple() {}public FourTuple(Object first, Object second, Object third, Object fourth) {this.first = first;this.second = second;this.third = third;this.fourth = fourth;}@Overridepublic String toString() {return "[" + this.first + "," + this.second + "," + this.third + "," + this.fourth + "]";}}比较正确的思路
使用两层循环遍历数组nums,计算nums[i]与nums[j]的乘积,将其当做key,value为key出现的次数。如果原来没有这个key的,就放入1;如果原来有这个key的,就在它的基础上加1。
这段代码如下:
for (int i = 0; i < len; i++) {int mul_result;for (int j = i + 1; j < len; j++) {mul_result = nums[i] * nums[j];hashMap.put(mul_result, hashMap.getOrDefault(mul_result, 0) + 1);}}如果value>=2的话,就证明存在有乘积相等的元组。
因为这段代码超时了,这里我发现"value与乘积相等元组个数之间"的关系,例如value=3,则有2+1=3个符合条件的元组,便使用了if语句判断value>=2,利用以下式子计算元组个数:
public static int cal(int x) {int sum = 0;x = x - 1;while (x >= 1) {sum += x;x--;}return sum;
}public static int tupleSameProduct(int[] nums) {...int res = 0;for (Map.Entry<Integer, Integer> entry : hashMap.entrySet()) {res += cal(entry.getValue());}return res;
}
力扣官方题解
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。![]() https://leetcode.cn/problems/tuple-with-same-product/solutions/2470655/tong-ji-yuan-zu-by-leetcode-solution-7yyy/应该是3 * (3 - 1) / 2 = 3,而不是2 + 1 = 3。前者时间复杂为O(1),后者需要遍历,时间复杂度为O(n)。一个元组有8种不一样的排序,如下所示
https://leetcode.cn/problems/tuple-with-same-product/solutions/2470655/tong-ji-yuan-zu-by-leetcode-solution-7yyy/应该是3 * (3 - 1) / 2 = 3,而不是2 + 1 = 3。前者时间复杂为O(1),后者需要遍历,时间复杂度为O(n)。一个元组有8种不一样的排序,如下所示
(2,6,3,4) , (2,6,4,3) , (6,2,3,4) , (6,2,4,3) (3,4,2,6) , (4,3,2,6) , (3,4,6,2) , (4,3,6,2)
所以每个元组就有n * (n - 1) / 2 * 8 = n * (n - 1) * 4。
代码
class Solution {public int tupleSameProduct(int[] nums) {int len = nums.length;HashMap<Integer, Integer> hashMap = new HashMap<>();int res = 0;for (int i = 0; i < len; i++) {int mul_result;for (int j = i + 1; j < len; j++) {mul_result = nums[i] * nums[j];hashMap.put(mul_result, hashMap.getOrDefault(mul_result, 0) + 1);}}for (Integer v : hashMap.values()) {res += v * (v - 1) * 4;}return res;}
}相关文章:
【Leetcode】【中等】1726.同积元组
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/tuple-with-same-product/ 给你…...
Git教程
文章目录 Git 介绍GIt历史Git 安装环境配置工作区、缓存区和仓库区(版本库)工作区(工作目录)暂存区仓库区git工作目录下文件的装填 Git 生成公钥及添加到gitlab或Gerrit上Git常用命令git stautsgit statu -sgit addgit commitgit reset1. git reset --ha…...
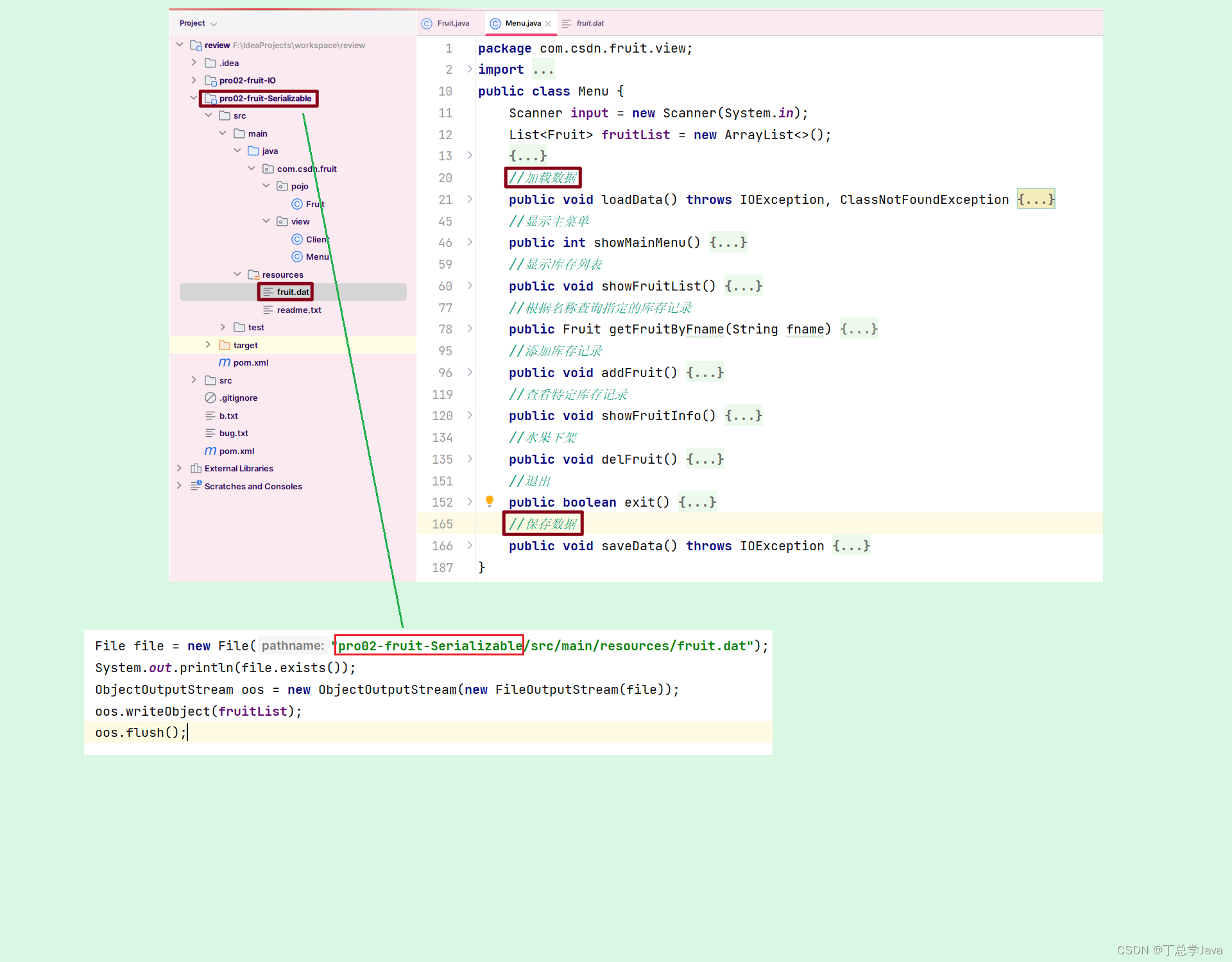
使用序列化技术保存数据 改进 IO流完成项目实战水果库存系统
上一节内容是 使用IO流完成项目实战水果库存系统https://blog.csdn.net/m0_65152767/article/details/133999972?spm1001.2014.3001.5501 package com.csdn.fruit.pojo; import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor; import java…...

0基础学习PyFlink——使用PyFlink的Sink将结果输出到外部系统
在《0基础学习PyFlink——使用PyFlink的SQL进行字数统计》一文中,我们直接执行了Select查询操作,在终端中直接看到了查询结果。 select word, count(1) as count from source group by word; ------------------------------------------------------ |…...

会声会影2024旗舰版详细功能介绍
随着网络视频的蓬勃发展,越来越多的人开始涉足视频剪辑领域,毕竟技多不压身嘛。在众多剪辑软件中,剪映和会声会影是备受新手青睐的两种。那么,会声会影和剪映哪个好呢?在它们之间,哪一个更适合初学者呢接&a…...

QtCreator 查看类帮助文档,快捷键操作:按两次F1 全屏帮助,Esc取消全屏
如何查看类帮助文档 选择类,按F1查看类帮助文档。 示例: #include <QLabel> // 将光标放在QLabel上,按F1右侧弹出的类帮助手册可视宽度很小,如果按两次 F1 键,帮助文档将会以全屏模式显示,以便更清…...
C语言文件操作(1)
C语言文件操作(1) 文章目录 C语言文件操作(1)一、理解文件1.概述2.分类①.正常角度②.文本文件和二进制文件 二、文件的打开和关闭1.流和标准流2.文件类型指针3.文件的打开和关闭以及使用类型 三、文件缓冲区 一、理解文件 1.概述…...
)
adb 操作命令(adb调试QT项目使用到的命令)
1.adb连接串口 获取root权限 adb root && adb remount && adb shell2.测试串口命令 stty -F /dev/ttyS4 cs8 -parenb -cstopb -echoecho "12345\n" > /dev/ttyS8cat /dev/ttyS4 &3.软件在安卓系统上的名字已经活动名称(下面是示…...
mysql下载和安装,使用
先下载安装 官方下载 已下载备份软件 安装,一路下一步设置环境变量 4. 打开一个cmd,输入mysql -u root -p...
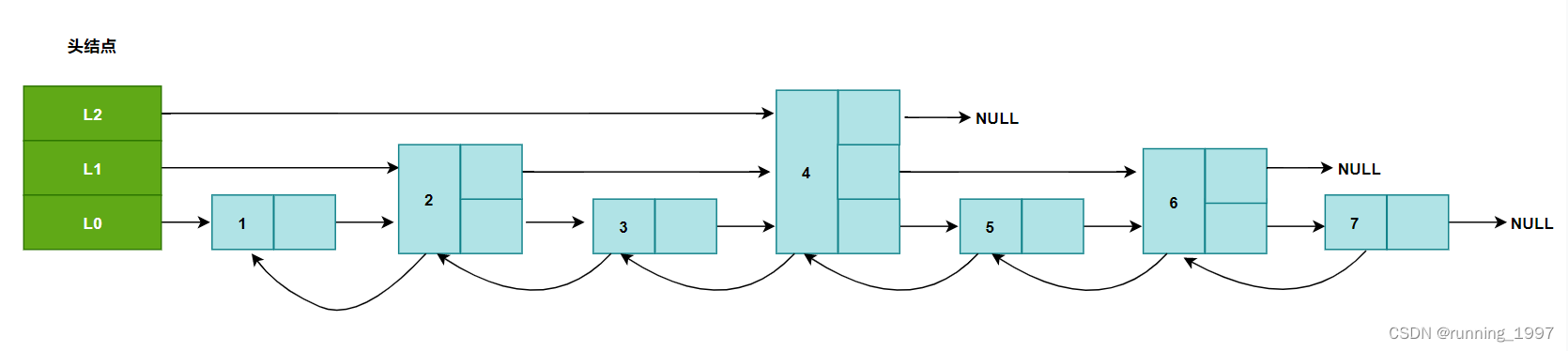
Redis底层核心数据结构详解
文章目录 一、深入String(SDS)1. 字符串简介2. SDS存在的意义3. SDS结构设计4. SDS与C字符串的区别4.1 常数复杂度获取字符串长度4.2 杜绝缓冲区溢出4.3 二进制安全4.4 SDS API 5 小结 二、深入List (QuickList)1. 链表节点结构设计2. Redis的链表实现的…...

如何学会从产品经理角度去思考问题?
如何学会从产品经理角度去思考问题? 从产品经理的角度思考问题意味着你需要关注产品从构思到上市全过程中的各个方面,包括用户需求、市场趋势、设计、开发、测试、上市后的用户反馈等。以下是一些策略和方法,帮助你培养从产品经理角度思考问…...

正则表达式的神奇世界:表达、匹配和提取
正则表达式的神奇世界:表达、匹配和提取 前言第一: 什么是正则表达式?第二: 字符匹配和量词:1. 字符匹配:2. 量词:3. 贪婪和非贪婪匹配: 第三:字符类和元字符1. 字符类&a…...

密码登录虽安全,但有时很麻烦!如何禁用或删除Windows 11中的密码登录
如果你想在Windows 11上自动登录,在本指南中,我们将向你展示如何删除你的帐户密码。 在Windows 11上,你可以至少通过三种方式从帐户中删除登录密码。在你的帐户上使用密码有助于保护你的计算机和文件免受来自internet或本地的未经授权的访问。然而,在某些情况下,密码可能…...

Python实现的快速排序代码
Python实现的快速排序代码 def bubble_sort(arr): n len(arr) for i in range(n): for j in range(0, n-i-1): if arr[j] > arr[j1]: arr[j], arr[j1] arr[j1], arr[j] return arr 冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,…...

【USRP】通信基带物理层历史
无线通信的基带物理层开发历史涵盖了从早期无线技术到当前复杂的移动通信标准的各种进步。以下是关于无线通信基带物理层开发的简要历史概述: 无线电初期:20世纪初,Guglielmo Marconi等人通过无线电进行了早期的无线通信尝试。这些早期的尝试…...
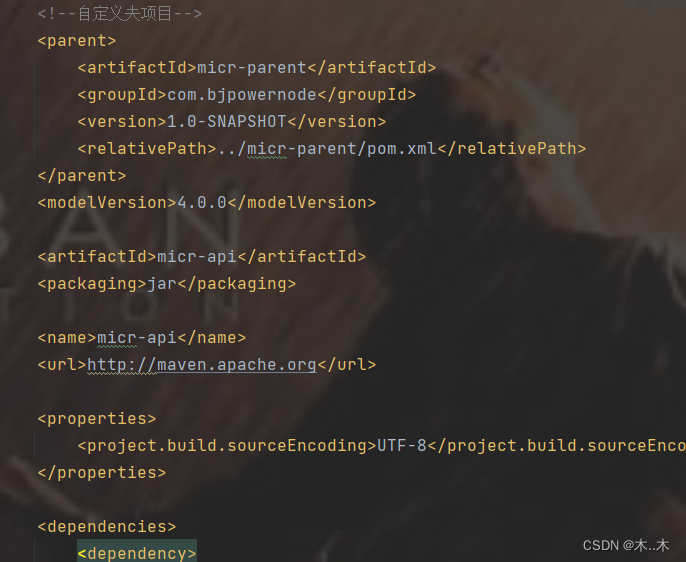
依靠继承与聚合,实现maven搭建分布式项目
简介聚合 对于复杂的Maven项目,一般建议采用多模块的方式来设计开发,便于后期维护管理。但是构建项目时,如果每次都需要按模块一个一个进行构建会十分麻烦,而Maven的聚合功能就可以很好的解决这个问题,当用户对聚合模…...
【java】A卷+B卷)
华为OD 叠积木(100分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...

vue重修之自定义项目、ESLint和代码规范修复
文章目录 VueCli 自定义创建项目ESlint代码规范及手动修复代码规范错误 VueCli 自定义创建项目 安装脚手架 (已安装) npm i vue/cli -g创建项目 vue create xxx选项 Vue CLI v5.0.8 ? Please pick a preset:Default ([Vue 3] babel, eslint)Default ([Vue 2] babel, eslint) …...
【java】A卷+B卷)
华为OD 完全二叉树非叶子部分后序遍历(200分)【java】A卷+B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应往年部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为OD…...

AI是未来?——神经网络篇
AI是未来?——神经网络篇 文章目录 AI是未来?——神经网络篇1. 神经网络小记问题记录: 1. 神经网络小记 疑问:假如让神经网络识别一张猫的图片,他经过了n个神经元节点最终识别为了狗。那么此时观察产生反应的这些神经…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
