华为OD 滑动窗口最大值(100分)【java】B卷
华为OD统一考试A卷+B卷 新题库说明
你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。
B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。
我将持续更新最新题目
获取更多免费题目可前往夸克网盘下载,请点击以下链接进入:
我用夸克网盘分享了「华为OD题库Java.zip」,点击链接即可保存。打开「夸克APP」
链接:https://pan.quark.cn/s/f59329c0173b
提取码:3p8Y
题目类型:栈和队列
题目描述:
有一个N个整数的数组,和一个长度为M的窗口,窗口从数组内的第一个数开始滑动直到窗口不能滑动为止, 每次窗口滑动产生一个窗口和(窗口内所有数的和),求窗口滑动产生的所有窗口和的最大值。
输入描述:
第一行输入一个正整数N,表示整数个数。(0<N<100000)
第二行输入N个整数,整数的取值范围为[-100,100]。
第三行输入一个正整数M,M代表窗口的大小,M<=100000,且M<=N。
输出描述:
窗口滑动产生所有窗口和的最大值。
示例 1 输入输出示例仅供调试,后台判题数据一般不包含示例
输入
相关文章:
【java】B卷)
华为OD 滑动窗口最大值(100分)【java】B卷
华为OD统一考试A卷+B卷 新题库说明 你收到的链接上面会标注A卷还是B卷。目前大部分收到的都是B卷。 B卷对应20022部分考题以及新出的题目,A卷对应的是新出的题目。 我将持续更新最新题目 获取更多免费题目可前往夸克网盘下载,请点击以下链接进入: 我用夸克网盘分享了「华为O…...
软件测试 (用例篇)
前言 上一篇博客讲述的是一次基本的测试过程。 在我们开始做了一段时间基础测试,熟悉了业务之后,往往会分配来写测试用例,并且在日常测试中,有时也需要补充测试用例到现有的案例库中。 在这里我们将回答以下问题 1、测试用例的…...

5G技术的飞速发展:连接未来
随着科技的日益进步,5G通讯技术已经成为了全球科技领域的热门话题。5G,即第五代移动通信技术,带来的不仅仅是更快的网络速度,它的高带宽和低延迟特性将为未来的数字世界奠定基础。 速度与效率的飞跃: 5G技术的最大亮点是它极高的下…...
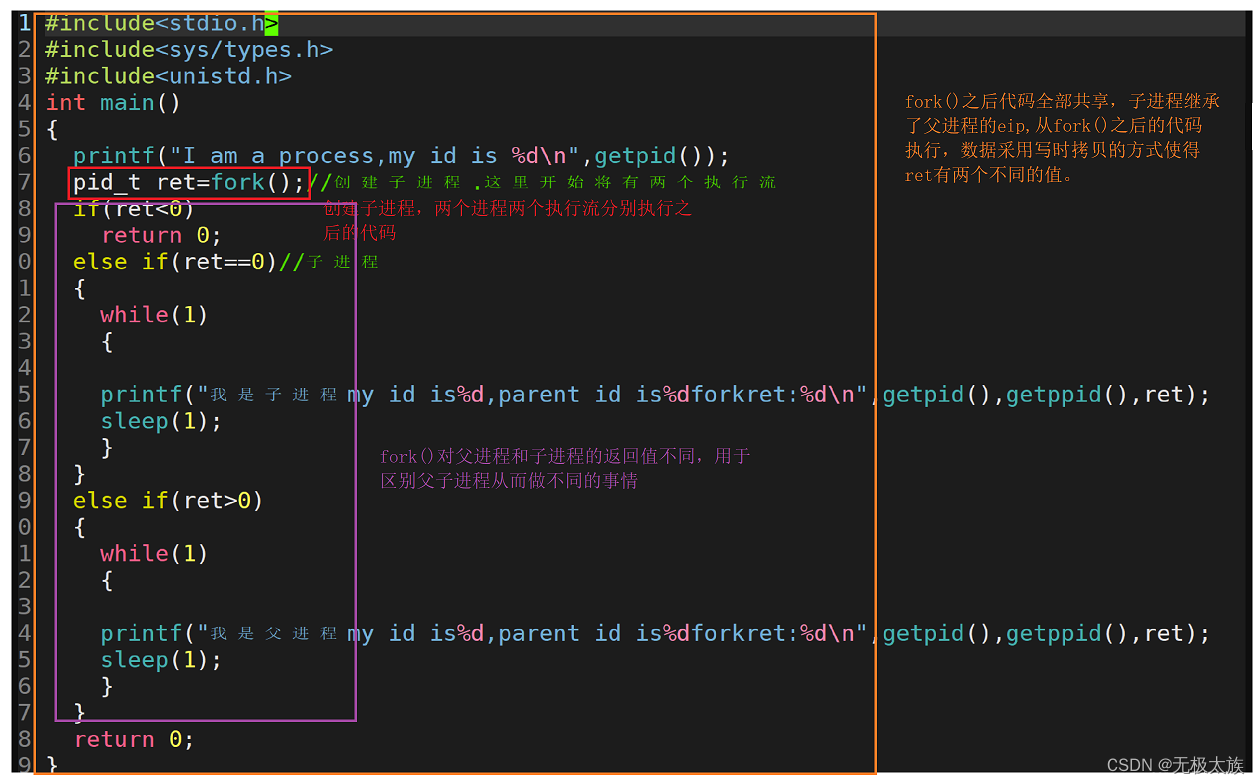
linux进程管理,一个进程的一生(喂饭级教学)
这篇文章谈谈linux中的进程管理。 一周爆肝,创作不易,望支持! 希望对大家有所帮助!记得收藏! 要理解进程管理,重要的是周边问题,一定要知其然,知其所以然。看下方目录就知道都是干货…...
】51 - QNX NFS Server + Android NFS Client 完整配置)
【SA8295P 源码分析 (四)】51 - QNX NFS Server + Android NFS Client 完整配置
【SA8295P 源码分析】51 - QNX NFS Server + Android NFS Client 完整配置 一、QNX 侧 NFS Server 修改:ip 为 192.168.118.21.1 配置拷贝 nfsd、rpcbind 到 /mnt 目录下1.2 配置 exports1.3 为NFS 共享目录挂载镜像1.4 修 startup.sh 开机自启动 nfsd Server1.5 关闭 QNX 防火…...
)
2023年10月23日--10月29日(主攻光追视频教程)
最好每周完成一样,将来每月完成一样,有成就感。也免得周末迷茫。 光锥目前还有56节, 周二到周五每天4小节。周六日每天20小节,应该可以完成。 即: 周二:9.5-9.8 周三:9.9-10.3 周四:…...

【Python语言速回顾】——函数模块类与对象
目录 引入 一、函数 1、函数概述 2、参数和返回值 3、函数的调用 二、模块 1、模块概述 2、模块应用实例 三、类与对象 1、面向对象概述 2、类 3、类的特点 引入 为了使程序实现的代码更加简单。需要把程序分成越来越小的组成部分,3种方式——函数、对象…...
【JavaEE】Java的多线程编程基础知识 -- 多线程篇(2)
Java多线程编程基础知识 一、多线程的创建二、Thread类常用的方法和API2.1 Thread 的几个常见的属性2.2 start 启动一个线程2.3 终止一个线程2.4 等待一个线程-join()2.5 线程休眠函数 -sleep() 三、线程状态3.1 观察所有线程的状态3.2 线程状态和线程转移的意义 四、线程安全&…...
)
MFC Windows 程序设计[330]之表头控件例程(附源码)
MFC Windows 程序设计[330]之表头控件例程 程序之美前言主体运行效果核心代码逻辑分析结束语程序之美 前言 MFC是微软公司提供的一个类库(class libraries),以C++类的形式封装了Windows API,并且包含一个应用程序框架,以减少应用程序开发人员的工作量。其中包含大量Wind…...

SettingsIntelligence
Android Settings 系列文章: Android Settings解析SettingsIntelligenceSettingsProvider 首语 Android Settings中搜索功能帮助我们可以快速访问设置项,进行自定义设置,以得到更佳的使用体验。Android Settings搜索的实现实际不在Setting…...

C#WPF Prism框架区域管理应用实例
本文实例演示C#WPFPrism框架区域管理应用实例 目录 一、Prism框架区域 二、不使用Prism框架的RegionManager 三、使用Prism框架的RegionManager 一、Prism框架区域...
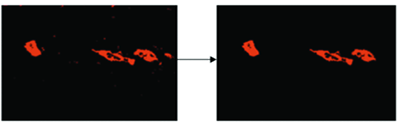
LabVIEW基于机器视觉的钢轨表面缺陷检测系统
LabVIEW基于机器视觉的钢轨表面缺陷检测系统 机器视觉检测技术和LabVIEW软件程序,可以实现轨道工件的表面质量。CMOS彩色工业相机采集的图像通过图像预处理、图像阈值分割、形态分析、特征定位和图案匹配进行处理和分析。图形显示界面采用LabVIEW软件编程设计&…...

Qt程序的发布和打包,任何电脑都可以安装
## 1. Qt程序的发布 当Qt程序编写完成通过IDE编译就可以得到对应的可执行程序,这个可执行程序在本地运行是完全没有问题的(因为在本地有Qt环境,程序运行过程中可以加载到相关的动态库),但是如果我们想把这个Qt程序给到其他小伙伴使用可能就会出问题了,原因如下: 对方电…...
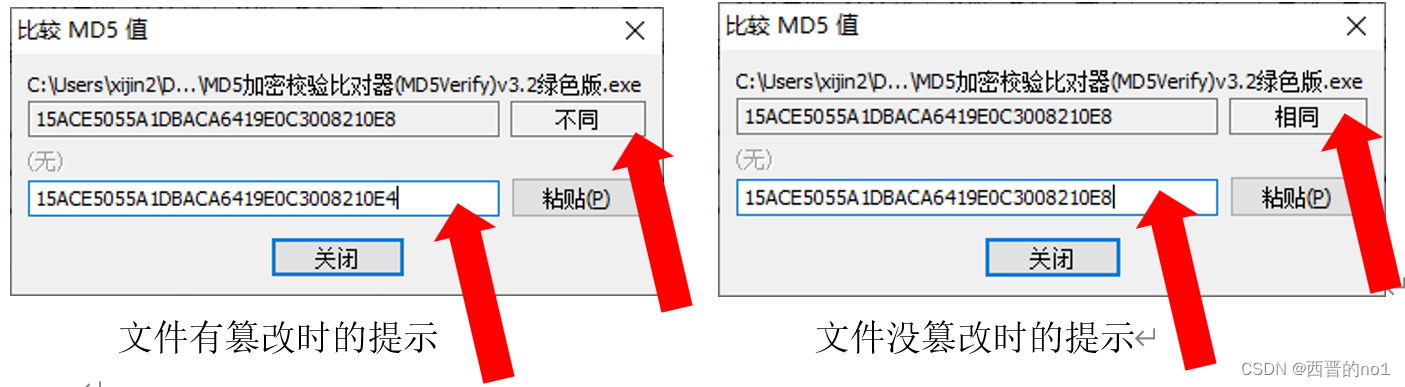
MD5生成和校验
MD5生成和校验 2021年8月19日席锦 任何类型的一个文件,它都只有一个MD5值,并且如果这个文件被修改过或者篡改过,它的MD5值也将改变。因此,我们会对比文件的MD5值,来校验文件是否是有被恶意篡改过。 什么是MD5ÿ…...

PostgreSQL 正则表达式匹配字段
在 PostgreSQL 数据库中,可以使用 ~ 和 !~ 操作符进行正则表达式的匹配和否定匹配。还可以使用 :: 操作符进行正则表达式的模式匹配。 例如,假设我们有一个名为 users 的表,其中有一个名为 email 的字段,我们可以使用以下 SQL 语句…...
关于iterm2的美化
iterm2 美化 笔者公司最近给发了一个新 M1 mac pro,所以一些软件需要重新安装。其中比较麻烦就是iterm2的一个美化工程 , 由于每次安装的效果都不尽相同所以这次写一个博客来记录一下 安装的过程 。 全程高能开始: 使用brew 来安装 iterm2 …...

Hook原理--逆向开发
今天我们将继续讲解逆向开发工程另一个重要内容--Hook原理讲解。Hook,可以中文译为“挂钩”或者“钩子”,逆向开发中改变程序运行的一种技术。按照如下过程进行讲解 Hook概述Hook技术方式fishhook原理及实例符号表查看函数名称总结 一、Hook概述 在逆…...

做数据可视化,谨记三大要点
数据可视化报表就是“一图胜千言”的最佳例子。数据可视化,也就是将数据图形化、图表化,以良好的视觉效果呈现数据,达到发现、分析、预测、监控、决策等目的。要想做出一份优秀的数据可视化报表,那就要在做报表时谨记三大要点&…...

软件设计原则-接口隔离原则讲解以及代码示例
接口隔离原则 一,介绍 1.前言 接口隔离原则(Interface Segregation Principle,ISP)是面向对象设计中的一个原则,提倡使用多个专门的接口,而不使用单一的大接口。它最早由Robert C. Martin在其《敏捷软件…...

yolov8x-p2 实现 tensorrt 推理
简述 在最开始的yolov8提供的不同size的版本,包括n、s、m、l、x(模型规模依次增大,通过depth, width, max_channels控制大小),这些都是通过P3、P4和P5提取图片特征; 正常的yolov8对象检测模型输出层是P3、…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
