模式识别——高斯分类器
模式识别——高斯分类器
- 需知
- 定义
- 特殊情况(方差一致)
- Sigmoid
需知
所有问题定义在分类问题下,基于贝叶斯决策
定义
条件概率为多元高斯分布,此时观测为向量 X = X 1 , X 2 , . . . , X n X={X_1,X_2,...,X_n} X=X1,X2,...,Xn,通过极大后验展开可以得到最优决策函数:

决策函数可以写为:

d d d就是马氏距离,代表两个高斯分布之间的距离。而 α \alpha α则代表了类别的先验。
特殊情况(方差一致)
方差一致的话分类器就是线性的。



Sigmoid
使用原始的BDR定义可以推导出,每个类别的概率概率为sigmoid函数(原始定义考虑观测的边缘概率,所以计算的就是概率(概率和为1),所以为sigmoid函数。而在决策时不考虑边缘概率,约掉了归一化参数,其实两者的判决边界仍然是相同的)


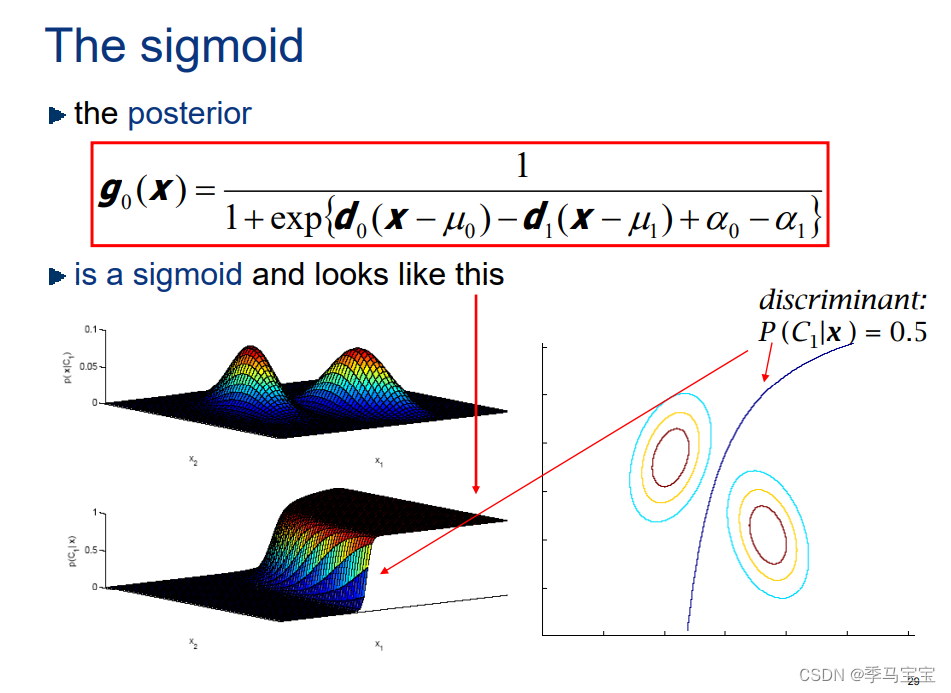
协方差一致有唯一分界线:

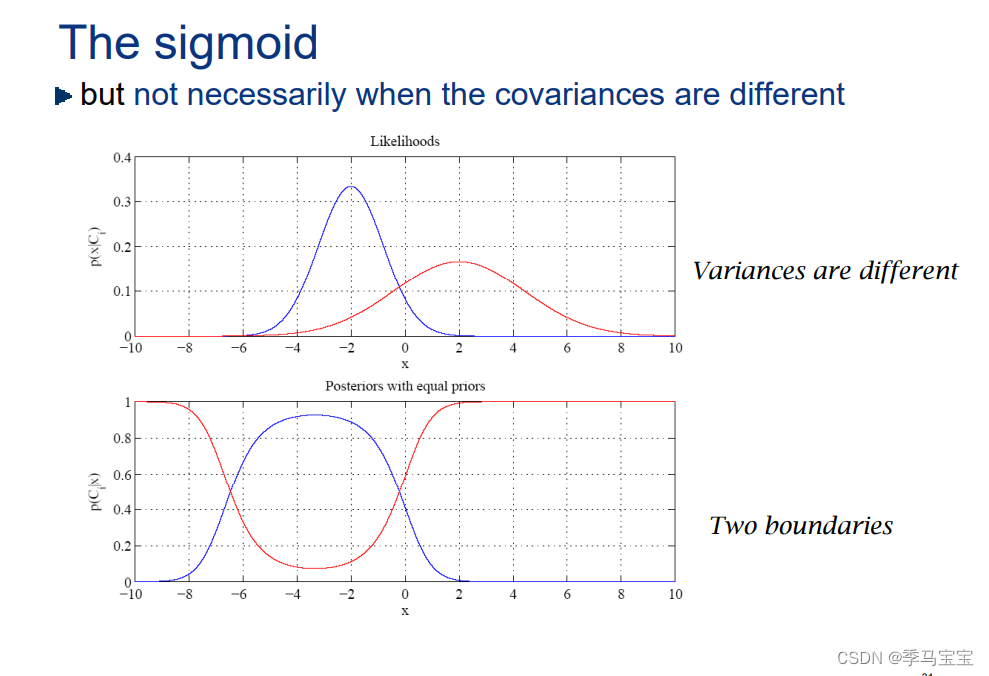
协方差不一致有两个分界线:
相关文章:

模式识别——高斯分类器
模式识别——高斯分类器 需知定义特殊情况(方差一致)Sigmoid 需知 所有问题定义在分类问题下,基于贝叶斯决策 定义 条件概率为多元高斯分布,此时观测为向量 X X 1 , X 2 , . . . , X n X{X_1,X_2,...,X_n} XX1,X2,...,Xn…...

LeetCode 15. 三数之和
三数之和 题目链接 15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意:**答案…...
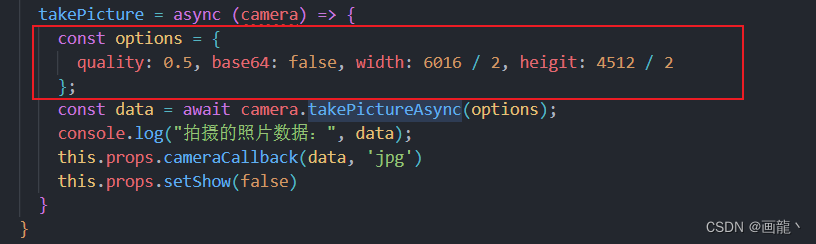
React-native-camera 在小米手机上拍照查看闪退
场景:为实现可拍照和录像的相机用react-native-camera这个库手写一个相机,发现了拍出来的图片在小米10上查看闪退 根据手机后台捕获的错误信息是什么玩意太大了(之前还以为是图片显示组件的问题) 改进:相机吊起的时候…...
nodejs+vue大学生社团管理系统
通过软件的需求分析已经获得了系统的基本功能需求,根据需求,将大学生社团管理系统平台功能模块主要分为管理员模块。管理员添加社团成员管理、社团信息管理,社长管理、用户注册管理等操作。 目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1…...
异步编程详解(.NET)
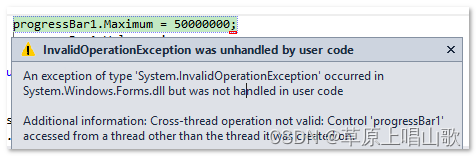
在之前写的一篇关于async和await的前世今生的文章之后,大家似乎在async和await提高网站处理能力方面还有一些疑问,很多网站本身也做了不少的尝试。今天我们再来回答一下这个问题,同时我会做一个async和await在WinForm中的尝试,并且…...

excel怎么固定前几行前几列不滚动?
在Excel中,如果你想固定前几行或前几列不滚动,可以通过以下几种方法来实现。详细的介绍如下: **固定前几行不滚动:** 1. 选择需要固定的行数。例如,如果你想要固定前3行,应该选中第4行的单元格。 2. 在E…...

elasticsearch完整学习
文章目录 elasticsearch一、概念二、ELK集群部署三、图形化界面 elasticsearch 一、概念 1、ELKStack简介(都是java架构,需要jdk底层) 什么是ELK?通俗来讲,ELK是由Elasticsearch、Logstash、Kibana 三个开源软件组成的…...
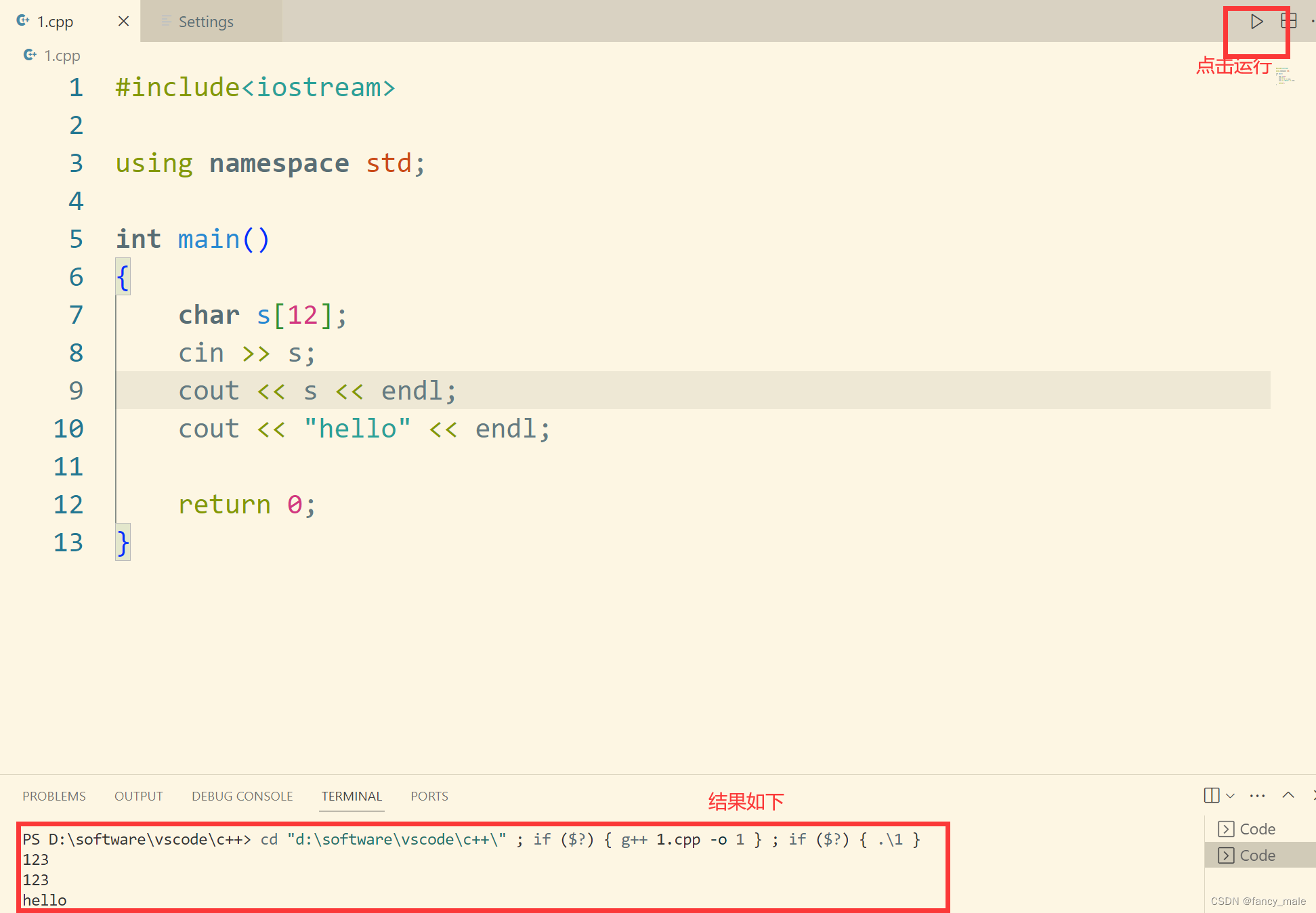
vscode Coder Runner 运行C++
1. 设置Code Runner 2. 防止输入读不到,把在终端运行勾上。 3. 设置minw/bin的环境变量 安装mingw教程:https://blog.csdn.net/fancy_male/article/details/133992000 4. 见图...

牛客网刷题-(2)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

FreeRTOS基础(如何学好FreeRTOS?)
目录 基础知识 进阶内容 后期“摆烂” 基础知识 实时操作系统 (RTOS):FreeRTOS是一个实时操作系统,它提供了任务管理、调度和同步等功能,在嵌入式系统中有效地管理多个任务。 任务(Task):任务是在RTOS…...
、条款44(概念明确)、条款45-50(杂项))
读书笔记:Effective C++ 2.0 版,条款43(多继承)、条款44(概念明确)、条款45-50(杂项)
条款43: 明智地使用多继承 并没有禁止,从概念上讲,多继承可能更符合真实世界。 条款44: 说你想说的;理解你所说的 概念明确 条款45: 弄清C在幕后为你所写、所调用的函数 隐性成本,看下编译后的c、asm源码。 条款46: 宁可编译和…...
最新Jn建站系统2.0 已集成各类源码 【附视频安装教程】
附视频安装教程|已集成各类源码 目前已集成的网站: 1.发卡网(最新) 2.代刷网(无需授权) 3. 博客网(自带模板) 4.易支付(稳定版) 5.个人导航网(简洁) 6.代理查询网 7.留言网 8.匿名网 9.表白墙(最新) 10.抽奖网 11.源码站 12.z-blog博客程序 13.织梦CM…...
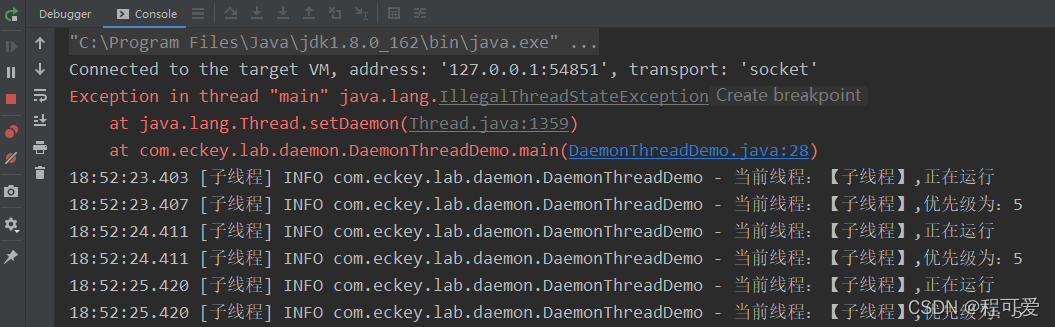
JAVA多线程基础篇--守护线程(Daemon Thread)
1.概述 JAVA中的线程主要分为两类:用户线程(User Thread)和守护线程(Daemon Thread)。JAVA语言中无论是线程还是线程池,默认都是用户线程,因此用户线程也被称为普通线程。守护线程也被称之为后台线程、服务线程或精灵…...

对知识蒸馏的一些理解
知识蒸馏是一种模型压缩技术,它通过从一个大模型(教师模型)中传输知识到一个小模型(学生模型)中来提高学生模型的性能,知识蒸馏也要用到真实的数据集标签。 软损失soft loss就是拿教师模型在蒸馏温度为T的…...
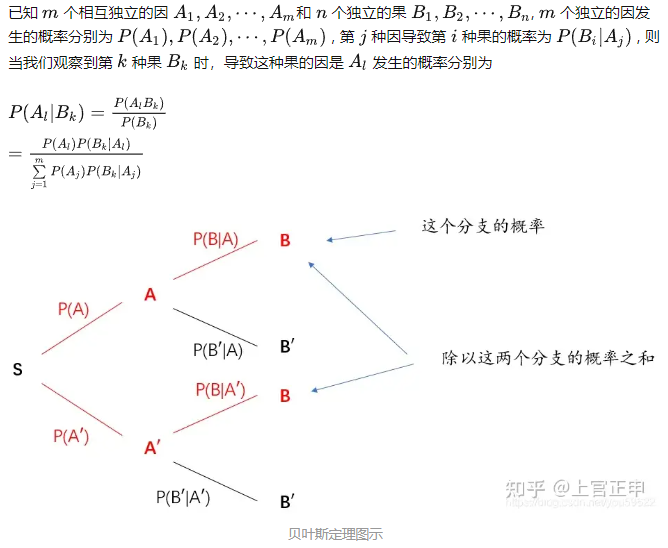
概率论_概率公式中的分号(;)、逗号(,)、竖线(|) 及其优先级
目录 1.概率公式中的分号(;)、逗号(,)、竖线(|) 2.各种概率相关的基本概念 2.1 联合概率 2.2 条件概率(定义) 2.3 全概率(乘法公式的加强版) 2.4 贝叶斯公式 贝叶斯定理的公式推导 1.概率公式中的分号(;)、逗号(,)、竖线(|) ; 分号代表前后是两类…...
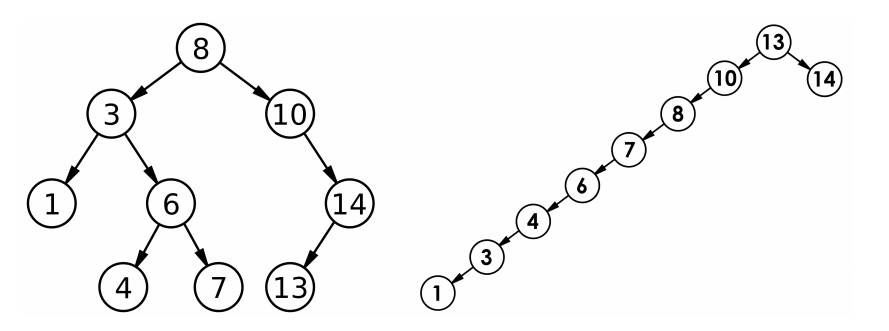
【C++】二叉树进阶 -- 详解
一、二叉搜索树概念 二叉搜索树 又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右子树不为空,则右子树上所有节点的值都大于根节点…...

K8S集群中Node节点资源不足导致Pod无法运行的故障排查思路
K8S集群中Node节点资源不足导致Pod无法运行的故障排查思路 Node节点资源不足可能会产生的故障 故障一:Pod数量太多超出物理节点的限制每一台Node节点中默认限制最多运行110个Pod资源,当一个应用程序有成百上千的Pod资源时,如果不扩容Node节…...
Node.js与npm版本比对
Node.js与npm版本比对 Node.js与npm版本比对版本对比表Node版本对比 Node.js与npm版本比对 我们在项目开发过程中,经常会遇到公司一些老的前端工程项目,而我们当前的node及npm版本都是相对比较新的了。 在运行以前工程时,会遇到相关环境不匹…...

智加科技与东风柳汽达成深度合作 自动驾驶重卡计划2024年初量产交付
(2023年10月19日,苏州)全球领先的重卡自动驾驶技术公司智加科技与东风柳汽宣布,双方共同开发的自动驾驶重卡H7计划2024年初实现量产交付。未来,双方将携手推出安全可靠、高性价比、性能卓越的自动驾驶重卡产品…...

mac下配置环境-node以及nvm
当前配置环境主要针对于mac下系统,需要提前安装brew包 如需要配置,可查阅:Brew包的基本安装(手把手教学)-CSDN博客 如果是window环境配置,分享一个不错的帖子:nvm的安装和使用(详细&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
