概率论_概率公式中的分号(；)、逗号(,)、竖线(|) 及其优先级

目录

1.概率公式中的分号(;)、逗号(,)、竖线(|)

2.各种概率相关的基本概念

2.1 联合概率

2.2 条件概率（定义）

2.3 全概率(乘法公式的加强版)

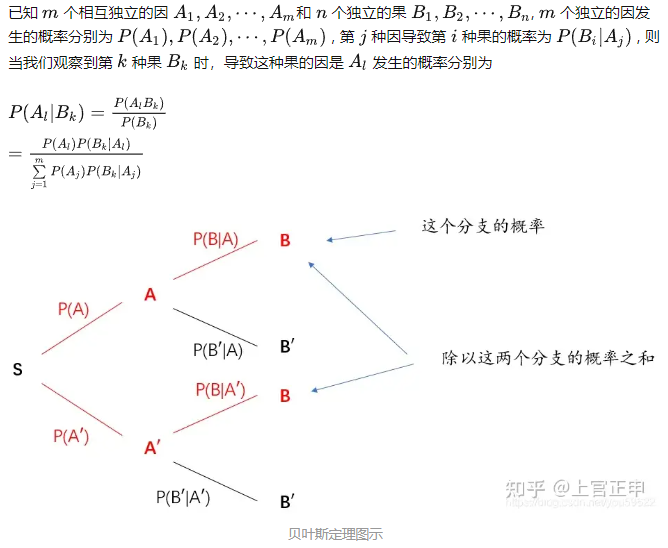
2.4 贝叶斯公式

贝叶斯定理的公式推导

---

1.概率公式中的分号(;)、逗号(,)、竖线(|)

•  ; 分号代表前后是两类东西，以概率P(x;θ)为例，分号前面是x样本，分号后边是模型参数。
  • 分号前 表示的是这个式子用来预测分布的随机变量x，分号后 表示所需的相关参数θ。
•  , 逗号代表两者地位平等，代表与的关系，有时可以省略，如联合概率P(AB), 等价于P(A,B)
•  | 竖线代表 if，以条件概率P(A|B)为例，就是如果B事件发生的条件下，发生A事件的概率。
• 优先级（先结合起来看）： ,  >  |  >  ; 
  • 有时候?:  分号 ; = 逗号 ，如P(x;θ) 和 P(x,θ)
  • 例子： P(A|B,C)表示在B，C的条件下，发生A的概率。
  • 例子：P(y∣x ; α,ω​)表示：x发生条件下y的条件概率，该条件概率模型用参数α,ω建模（或者说用参数a,ω表示）

理解1：

理解2：

2.各种概率相关的基本概念

2.1 联合概率

        事件A和事件B同时发生（交集）的概率，表示 P(AB)，称为联合概率，也可表示为P(A,B)，或者P(A∩B)， 即： 

P(AB) = P(A,B) = P(A∩B)

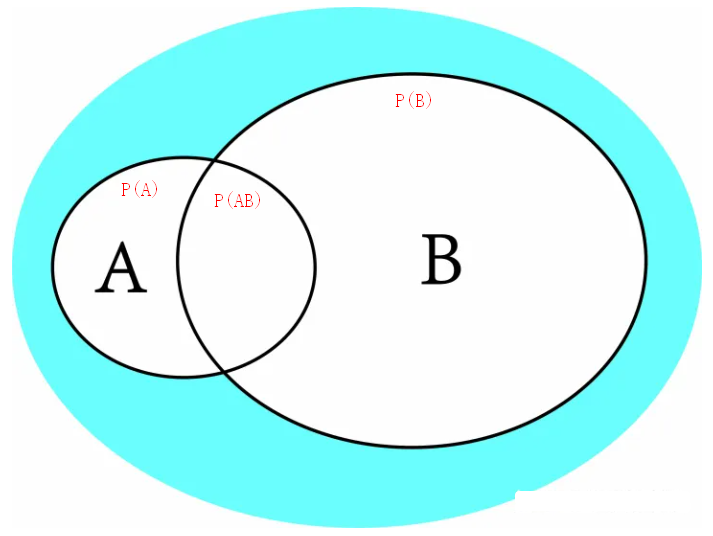
2.2 条件概率（定义）

        设A，B是随机试验E的两个随机试验，且P(B)>0，称

为在事件B发生的条件下，事件A发生的条件概率。图示如下

由此得到乘法公式：

2.3 全概率(乘法公式的加强版)

图示可表示为： 

2.4 贝叶斯公式

可有上面2个乘法式子得到：

贝叶斯定理，或条件概率定理

理解：通过从因到果的概率来计算从果到因的概率。更透彻地说就是我们通过各个因的概率以及各个因产生各个果的概率，不仅可以算出来各个果发生的概率，更进一步我们还能反推出各个果由各个因产生的概率。

贝叶斯定理的公式推导

参考： 

简单理解函数f(x；θ)中分号的含义_f(x;θ)是什么意思_xiongxyowo的博客-CSDN博客

条件概率公式以及逗号与竖线的“优先级” - 百度文库

概率论基础3——条件概率 - 知乎

概率公式中的分号、逗号、竖线_数学函数内逗号分号什么意思-CSDN博客

概率论-概率中逗号分号和竖线_概率表示中的 , |-CSDN博客

概率与统计进阶（1）——概率统计的基础概念：条件概率、全概率、贝叶斯公式-CSDN博客