TFHE 的全同态模结构(FHE Module Structure)
参考文献:
- [CGGI20] Chillotti I, Gama N, Georgieva M, et al. TFHE: fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.
- [BGGJ20] Boura C, Gama N, Georgieva M, et al. Chimera: Combining ring-lwe-based fully homomorphic encryption schemes[J]. Journal of Mathematical Cryptology, 2020, 14(1): 316-338.
文章目录
- Notation
- TLWE
- TRLWE
- TGSW
- TRGSW
- FHE Module Structure
Notation
代数结构:
- 实数环面 T = R / Z = [ 0 , 1 ) \mathbb T = \mathbb R/\mathbb Z = [0,1) T=R/Z=[0,1)
- 整系数多项式环 R = Z [ x ] / ( x N + 1 ) R = \mathbb Z[x]/(x^N+1) R=Z[x]/(xN+1)
- 系数取自整环 A ∈ { Z , R , C } A \in \{\mathbb Z,\mathbb R,\mathbb C\} A∈{Z,R,C},多项式环 R A = R ⊗ Z A = A [ x ] / ( x N + 1 ) R_A = R \otimes_\mathbb Z A=A[x]/(x^N+1) RA=R⊗ZA=A[x]/(xN+1)
- 商环 R q = R / q R = Z q [ x ] / ( x N + 1 ) R_q=R/qR = \mathbb Z_q[x]/(x^N+1) Rq=R/qR=Zq[x]/(xN+1),自然满射 π q : R → R q \pi_q:R \to R_q πq:R→Rq 是同态
- 商群 T R = R R / R Z = T [ x ] / ( x N + 1 ) \mathbb T_R = R_\mathbb R/R_\mathbb Z = \mathbb T[x]/(x^N+1) TR=RR/RZ=T[x]/(xN+1),它是 R R R 左模(但不是环),环 R R R 左作用模 T R \mathbb T_R TR 称为 “外积”
Lipschitz 函数:斜率绝对值不大于 κ \kappa κ,因此被两个一次函数夹逼。
集中分布(concentrated distributions):除了可忽略的测度,概率分布的支撑集是某个半径 1 / 2 1/2 1/2 球体的子集;此时,这个实数环面上的概率分布是良的,存在良定义的期望、标准差。
TLWE
底层的代数结构,
- 秘钥空间: B ⊆ Z N \mathcal B \subseteq \mathbb Z^N B⊆ZN,小范数的整数向量集合
- 明文空间: T \mathbb T T,是 Z \mathbb Z Z 模(不是环,乘法未定义)
- 密文空间: T N × T = T N + 1 \mathbb T^N \times \mathbb T = \mathbb T^{N+1} TN×T=TN+1,是 Z \mathbb Z Z 模(不是环,同态乘法不自然)
- 相位函数: ϕ s : ( a , b ) ↦ b − s t a \phi_s: (a,b) \mapsto b-s^ta ϕs:(a,b)↦b−sta,是 κ \kappa κ Lipschitz 函数,其中 κ \kappa κ 很小(关于环面上 l ∞ l_\infty l∞ 范数)
不考虑(具有同态性质的)纠错码,
对称密钥:
- 均匀采样 s ← B s \gets \mathcal B s←B,它是整系数的短向量
加密:
- 明文 μ ∈ T \mu \in \mathbb T μ∈T
- 均匀采样 a ← T N a \gets \mathbb T^N a←TN,零中心高斯采样 e ← T e \gets \mathbb T e←T
- 计算 b : = s t a + e ∈ T b := s^ta+e \in \mathbb T b:=sta+e∈T,满足 ϕ s ( a , b ) = e ≈ 0 \phi_s(a,b)=e \approx 0 ϕs(a,b)=e≈0
- 密文 c : = ( a , b ) + ( 0 , μ ) c:=(a,b)+(0,\mu) c:=(a,b)+(0,μ) 是长度 N + 1 N+1 N+1 的列向量
解密:
- 密文 ( a , b ′ ) ∈ T N × T (a,b') \in \mathbb T^N \times \mathbb T (a,b′)∈TN×T
- 计算 ϕ s ( a , b ′ ) = e + μ ∈ T \phi_s(a,b') = e+\mu \in \mathbb T ϕs(a,b′)=e+μ∈T
- 带噪明文 μ + e \mu+e μ+e 是一个随机变量,均值是 μ \mu μ
同态运算:
- 根据 Z \mathbb Z Z 模的加法, μ 1 + μ 2 ⟺ c 1 + c 2 \mu_1+\mu_2 \iff c_1+c_2 μ1+μ2⟺c1+c2
- 根据 Z \mathbb Z Z 模的环作用, k ⋅ μ ⟺ k ⋅ c k \cdot \mu \iff k \cdot c k⋅μ⟺k⋅c,其中 k ∈ Z k \in \mathbb Z k∈Z
- 不支持乘法运算(BGV/BFV 的密文张量积不自然)
TRLWE
底层的代数结构,
- 秘钥空间: B ⊆ R \mathcal B \subseteq R B⊆R,小范数的整系数多项式集合
- 明文空间: T R \mathbb T_R TR,是 R R R 模(不是环,乘法未定义)
- 密文空间: T R × T R = T R 2 \mathbb T_R \times \mathbb T_R = \mathbb T_R^2 TR×TR=TR2,是 R R R 模(不是环,同态乘法不自然)
- 相位函数: ϕ s : ( a , b ) ↦ b − s ⋅ a \phi_s: (a,b) \mapsto b-s\cdot a ϕs:(a,b)↦b−s⋅a,是 κ \kappa κ Lipschitz 函数,其中 κ \kappa κ 很小(关于环面上 l ∞ l_\infty l∞ 范数)
不考虑(具有同态性质的)纠错码,
对称密钥:
- 均匀采样 s ← B s \gets \mathcal B s←B,它是短的整系数多项式
加密:
- 明文 μ ∈ T R \mu \in \mathbb T_R μ∈TR
- 均匀采样 a ← T R a \gets \mathbb T_R a←TR,零中心高斯采样 e ← T R e \gets \mathbb T_R e←TR
- 计算 b : = s ⋅ a + e ∈ T R b := s\cdot a+e \in \mathbb T_R b:=s⋅a+e∈TR,满足 ϕ s ( a , b ) = e ≈ 0 \phi_s(a,b)=e \approx 0 ϕs(a,b)=e≈0
- 密文 c : = ( a , b ) + ( 0 , μ ) c:=(a,b)+(0,\mu) c:=(a,b)+(0,μ) 是长度 2 2 2 的列向量
解密:
- 密文 ( a , b ′ ) ∈ T R × T R (a,b') \in \mathbb T_R \times \mathbb T_R (a,b′)∈TR×TR
- 计算 ϕ s ( a , b ′ ) = e + μ ∈ T R \phi_s(a,b') = e+\mu \in \mathbb T_R ϕs(a,b′)=e+μ∈TR
- 带噪明文 μ + e \mu+e μ+e 是一个随机变量,均值是 μ \mu μ
同态运算:
- 根据 R R R 模的加法, μ 1 + μ 2 ⟺ c 1 + c 2 \mu_1+\mu_2 \iff c_1+c_2 μ1+μ2⟺c1+c2
- 根据 R R R 模的环作用, k ⋅ μ ⟺ k ⋅ c k \cdot \mu \iff k \cdot c k⋅μ⟺k⋅c,其中 k ∈ R k \in R k∈R
- 不支持乘法运算(BGV/BFV 的密文张量积不自然)
TGSW
底层的代数结构,
- 秘钥空间: B ⊆ Z N \mathcal B \subseteq \mathbb Z^N B⊆ZN,小范数的整数向量集合
- 明文空间: Z \mathbb Z Z,是整数环(定义了乘法)
- 密文空间: T N × ( N + 1 ) l × T N l = T ( N + 1 ) × ( N + 1 ) l \mathbb T^{N\times (N+1)l} \times \mathbb T^{Nl}=\mathbb T^{(N+1) \times (N+1)l} TN×(N+1)l×TNl=T(N+1)×(N+1)l,是 Z \mathbb Z Z 模(同态乘法自然)
- 相位函数: ϕ s : ( A , b ) ↦ b − s t A \phi_s: (A,b) \mapsto b-s^tA ϕs:(A,b)↦b−stA,是 κ \kappa κ Lipschitz 函数,其中 κ \kappa κ 很小(关于环面上 l ∞ l_\infty l∞ 范数)
采用 Gadget 纠错码,设置行向量 g = [ 2 − 1 , 2 − 2 , ⋯ , 2 − l ] g=[2^{-1},2^{-2},\cdots,2^{-l}] g=[2−1,2−2,⋯,2−l],其中 l l l 是实数环面的离散化精度 2 − l Z / Z ⊆ T 2^{-l}\mathbb Z/\mathbb Z \subseteq \mathbb T 2−lZ/Z⊆T,
G = I N + 1 ⊗ g = [ g g ⋱ g ] ∈ Z ( N + 1 ) × ( N + 1 ) l G = I_{N+1} \otimes g = \begin{bmatrix} g&\\ &g&\\ &&\ddots&\\ &&& g \end{bmatrix} \in \mathbb Z^{(N+1) \times (N+1)l} G=IN+1⊗g= gg⋱g ∈Z(N+1)×(N+1)l
对应的逆变换 G − 1 G^{-1} G−1 是个随机化程序,满足 ∥ G G − 1 ( C ) − C ∥ ∞ ≤ 2 − ( l + 1 ) \|GG^{-1}(C)-C\|_\infty \le 2^{-(l+1)} ∥GG−1(C)−C∥∞≤2−(l+1),对于任意的 C ∈ T ( N + 1 ) × ( N + 1 ) l C \in \mathbb T^{(N+1) \times (N+1)l} C∈T(N+1)×(N+1)l
对称密钥:
- 均匀采样 s ← B s \gets \mathcal B s←B,它是整系数的短向量
加密:
- 明文 μ ∈ Z \mu \in \mathbb Z μ∈Z,编码为有限精度的环面矩阵 μ G ∈ T ( N + 1 ) × ( N + 1 ) l \mu G \in \mathbb T^{(N+1) \times (N+1)l} μG∈T(N+1)×(N+1)l
- 均匀采样 A ← T N × ( N + 1 ) l A \gets \mathbb T^{N \times (N+1)l} A←TN×(N+1)l,零中心高斯采样 e ← T ( N + 1 ) l e \gets \mathbb T^{(N+1)l} e←T(N+1)l(行向量)
- 计算 b : = s t A + e ∈ T ( N + 1 ) l b := s^tA+e \in \mathbb T^{(N+1)l} b:=stA+e∈T(N+1)l(行向量),满足 ϕ s ( A , b ) = e ≈ 0 \phi_s(A,b)=e \approx 0 ϕs(A,b)=e≈0
- 密文 c : = [ A b ] + μ G c:=\begin{bmatrix}A\\b\end{bmatrix}+\mu G c:=[Ab]+μG
解密:
- 密文 [ A ′ b ′ ] ∈ T ( N + 1 ) × ( N + 1 ) l \begin{bmatrix}A'\\b'\end{bmatrix} \in \mathbb T^{(N+1) \times (N+1)l} [A′b′]∈T(N+1)×(N+1)l
- 计算 ϕ s ( A ′ , b ′ ) = e + μ ( − s , 1 ) G ∈ T ( N + 1 ) l \phi_s(A',b') = e+\mu (-s,1)G \in \mathbb T^{(N+1)l} ϕs(A′,b′)=e+μ(−s,1)G∈T(N+1)l(行向量)
- 截取长度 l l l 的尾巴,得到的 e ′ + μ g ∈ T l e'+\mu g \in \mathbb T^l e′+μg∈Tl 是含噪码字,均值 μ g \mu g μg
同态运算:
-
根据 Z \mathbb Z Z 模的加法, μ 1 + μ 2 ⟺ c 1 + c 2 \mu_1+\mu_2 \iff c_1+c_2 μ1+μ2⟺c1+c2
-
根据 Z \mathbb Z Z 模的环作用, k ⋅ μ ⟺ k ⋅ c k \cdot \mu \iff k \cdot c k⋅μ⟺k⋅c,其中 k ∈ Z k \in \mathbb Z k∈Z
-
同态乘法,明文空间 μ 1 ∈ Z \mu_1 \in \mathbb Z μ1∈Z 对于密文空间 G − 1 ( μ 2 G ) ∈ T ( N + 1 ) × ( N + 1 ) l G^{-1}(\mu_2G) \in \mathbb T^{(N+1) \times (N+1)l} G−1(μ2G)∈T(N+1)×(N+1)l 的环作用,
C 1 ⋅ G − 1 ( C 2 ) = ( [ A 1 ∣ b 1 ] + μ 1 G ) ⋅ G − 1 ( ( [ A 2 ∣ b 2 ] + μ 2 G ) ) = ( [ A 1 ∣ b 1 ] ⋅ G − 1 ( C 2 ) + μ 1 C 2 ) + μ 1 μ 2 G \begin{aligned} &\,\, C_1 \cdot G^{-1}(C_2)\\ =&\,\, ([A_1|b_1]+\mu_1 G) \cdot G^{-1}(([A_2|b_2]+\mu_2 G))\\ =&\,\, \left([A_1|b_1] \cdot G^{-1}(C_2) + \mu_1C_2\right) + \mu_1\mu_2G \end{aligned} ==C1⋅G−1(C2)([A1∣b1]+μ1G)⋅G−1(([A2∣b2]+μ2G))([A1∣b1]⋅G−1(C2)+μ1C2)+μ1μ2G它的噪声增长是不平衡的,导出了乘法链的右结合性。
TRGSW
底层的代数结构,
- 秘钥空间: B ⊆ R \mathcal B \subseteq R B⊆R,小范数的整系数多项式集合
- 明文空间: R R R,是整系数多项式环(定义了乘法)
- 密文空间: T R 2 l × T R 2 l = T R 2 × 2 l \mathbb T_R^{2l} \times \mathbb T_R^{2l} = \mathbb T_R^{2 \times 2l} TR2l×TR2l=TR2×2l,是 R R R 模(同态乘法自然)
- 相位函数: ϕ s : ( A , b ) ↦ b − s A \phi_s: (A,b) \mapsto b-sA ϕs:(A,b)↦b−sA,是 κ \kappa κ Lipschitz 函数,其中 κ \kappa κ 很小(关于环面上 l ∞ l_\infty l∞ 范数)
采用 Gadget 纠错码,设置 g = [ 2 − 1 , 2 − 2 , ⋯ , 2 − l ] g=[2^{-1},2^{-2},\cdots,2^{-l}] g=[2−1,2−2,⋯,2−l] 是行向量,其中 l l l 是环面的离散化精度 2 − l R Z / R Z ⊆ T R 2^{-l}R_\mathbb Z /R_\mathbb Z \subseteq \mathbb T_R 2−lRZ/RZ⊆TR,
G = g ⊗ I 2 = [ I , 2 I , ⋯ , 2 − l I ] ∈ T R 2 × 2 l G = g \otimes I_2 = \begin{bmatrix} I, 2I, \cdots, 2^{-l}I \end{bmatrix} \in \mathbb T_R^{2 \times 2l} G=g⊗I2=[I,2I,⋯,2−lI]∈TR2×2l
对应的逆变换 G − 1 G^{-1} G−1 是个随机化程序,满足 ∥ G G − 1 ( C ) − C ∥ ∞ ≤ 2 − ( l + 1 ) \|GG^{-1}(C)-C\|_\infty \le 2^{-(l+1)} ∥GG−1(C)−C∥∞≤2−(l+1),对于任意的 C ∈ T R 2 l × 2 C \in \mathbb T_R^{2l \times 2} C∈TR2l×2
对称密钥:
- 均匀采样 s ← B s \gets \mathcal B s←B,它是短的整系数多项式
加密:
- 明文 μ ∈ R \mu \in R μ∈R,编码为有限精度的环面矩阵 μ G ∈ T R 2 × 2 l \mu G \in \mathbb T_R^{2\times 2l} μG∈TR2×2l
- 均匀采样 A ← T R 2 l A \gets \mathbb T_R^{2l} A←TR2l(行向量),零中心高斯采样 e ← T R 2 l e \gets \mathbb T_R^{2l} e←TR2l(行向量)
- 计算 b : = s A + e ∈ T R N l b := sA+e \in \mathbb T_R^{Nl} b:=sA+e∈TRNl(行向量),满足 ϕ s ( A , b ) = e ≈ 0 \phi_s(A,b)=e \approx 0 ϕs(A,b)=e≈0
- 密文 c : = [ A b ] + μ G c:=\begin{bmatrix}A\\b\end{bmatrix}+\mu G c:=[Ab]+μG
解密:
- 密文 ( A ′ , b ′ ) ∈ T R 2 l × T R 2 l (A',b') \in \mathbb T_R^{2l} \times \mathbb T_R^{2l} (A′,b′)∈TR2l×TR2l
- 计算 ϕ s ( A ′ , b ′ ) = e + μ ( − s , 1 ) G ∈ T R 2 l \phi_s(A',b') = e+\mu(-s,1)G \in \mathbb T_R^{2l} ϕs(A′,b′)=e+μ(−s,1)G∈TR2l(行向量)
- 截取索引 2 , 4 , ⋯ , 2 l 2,4,\cdots,2l 2,4,⋯,2l 的元素,得到的 e ′ + μ g ∈ T R l e'+\mu g \in \mathbb T_R^l e′+μg∈TRl 是含噪码字,均值 μ g \mu g μg
同态运算:
-
根据 R R R 模的加法, μ 1 + μ 2 ⟺ C 1 + C 2 \mu_1+\mu_2 \iff C_1+C_2 μ1+μ2⟺C1+C2
-
根据 R R R 模的环作用, k ⋅ μ ⟺ k ⋅ C k \cdot \mu \iff k \cdot C k⋅μ⟺k⋅C,其中 k ∈ R k \in R k∈R
-
同态乘法,明文空间 μ 1 ∈ R \mu_1 \in R μ1∈R 对于密文空间 G − 1 ( μ 2 G ) ∈ T R 2 × 2 l G^{-1}(\mu_2G) \in \mathbb T_R^{2 \times 2l} G−1(μ2G)∈TR2×2l 的环作用,
C 1 ⋅ G − 1 ( C 2 ) = ( [ A 1 ∣ b 1 ] + μ 1 G ) ⋅ G − 1 ( ( [ A 2 ∣ b 2 ] + μ 2 G ) ) = ( [ A 1 ∣ b 1 ] ⋅ G − 1 ( C 2 ) + μ 1 C 2 ) + μ 1 μ 2 G \begin{aligned} &\,\, C_1 \cdot G^{-1}(C_2)\\ =&\,\, ([A_1|b_1]+\mu_1 G) \cdot G^{-1}(([A_2|b_2]+\mu_2 G))\\ =&\,\, \left([A_1|b_1] \cdot G^{-1}(C_2) + \mu_1C_2\right) + \mu_1\mu_2G \end{aligned} ==C1⋅G−1(C2)([A1∣b1]+μ1G)⋅G−1(([A2∣b2]+μ2G))([A1∣b1]⋅G−1(C2)+μ1C2)+μ1μ2G它的噪声增长是不平衡的,导出了乘法链的右结合性。
FHE Module Structure
非正式地,全同态模结构是五元元组 ( R , Π R , M , Π M , ⊡ ) (R,\Pi_R,M,\Pi_M,\boxdot) (R,ΠR,M,ΠM,⊡):
-
环 R R R 的加密方案 Π R = ( E n c R , D e c R ) \Pi_R=(Enc_R,Dec_R) ΠR=(EncR,DecR),它的密文空间是 C R \mathcal C_R CR
-
模 M M M 的同态加密方案 Π M = ( E n c M , D e c M ) \Pi_M=(Enc_M,Dec_M) ΠM=(EncM,DecM),它的密文空间是 C M \mathcal C_M CM
-
两个方案的密文之间的运算 ⊡ : C R × C M → C M \boxdot: \mathcal C_R \times \mathcal C_M \to \mathcal C_M ⊡:CR×CM→CM(外积),使得
D e c M ( E n c R ( r ) ⊡ E n c M ( m ) ) = r ⋅ m , ∀ r ∈ R , ∀ m ∈ M Dec_M(Enc_R(r) \boxdot Enc_M(m)) = r \cdot m,\forall r \in R,\forall m \in M DecM(EncR(r)⊡EncM(m))=r⋅m,∀r∈R,∀m∈M
TFHE 就是让 TGSW 和 TLWE、TRGSW 和 TRLWE 组成了全同态模结构,从而实现了 “外积”,
- 元组 ( ( Z , TGSW ) , ( T , TLWE ) ) ((\mathbb Z,\text{TGSW}),(\mathbb T,\text{TLWE})) ((Z,TGSW),(T,TLWE)),组成了环 Z \mathbb Z Z 模 T \mathbb T T 的全同态模结构
- 元组 ( ( R , TRGSW ) , ( T R , TRLWE ) ) ((R,\text{TRGSW}),(\mathbb T_R,\text{TRLWE})) ((R,TRGSW),(TR,TRLWE)),组成了环 R R R 模 T R \mathbb T_R TR 的全同态模结构
相关文章:
)
TFHE 的全同态模结构(FHE Module Structure)
参考文献: [CGGI20] Chillotti I, Gama N, Georgieva M, et al. TFHE: fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.[BGGJ20] Boura C, Gama N, Georgieva M, et al. Chimera: Combining ring-lwe-based ful…...

rapidocr_paddle[gpu]:GPU端推理库来了
简介 rapidocr_paddle系列包是基于PaddlePaddle框架作为推理引擎的,支持CPU和GPU上推理。值得说明的是,这个包和PaddleOCR相比,代码基本都是一样的,只不过这个库将里面核心推理代码抽了出来,更加精简而已。 推荐GPU上…...
PKU 概率论+数理统计+建模 期中考复习总结
目录 计算条件概率计算概率(放回与不放回)生成随机数算法Linear Congruential Method判断是否是full period Uniformity (test of frequency)1.Chi-Square testmethodreminderexample 2.Kolmogorov-Sminov testmethodexample Independence (test of auto…...
Kubernetes技术与架构-网络 3
Kubernetes集群支持为Pod或者Service申请IPV4或者IPV6的地址空间。 kube-apiserver --service-cluster-ip-range<IPv4 CIDR>,<IPv6 CIDR> kube-controller-manager --cluster-cidr<IPv4 CIDR>,<IPv6 CIDR> --service-cluster-ip-range<IPv4 CI…...

pycharm转移缓存目录
原来的缓存目录为C:\Users\86176\AppData\Local\JetBrains,各种配置文件、缓存文件随着pycharm的使用堆积在这里,导致C盘逐渐爆满。 因此需要将缓存目录转移至D盘。首先需要了解缓存目录的知识。 PyCharm 和其他 JetBrains 的 IDE 通常会有两个关键的目…...

python 2组list绘制拟合曲线、计算拟合方程 R^2
import matplotlib.pyplot as plt import numpy as np # plt.rcParams[font.family] SimHei # 指定使用中文字体,例如宋体(SimHei)def Curve_Fitting(x, y, deg):parameter np.polyfit(x, y, deg) #拟合deg次多项式p np.poly1d(paramet…...
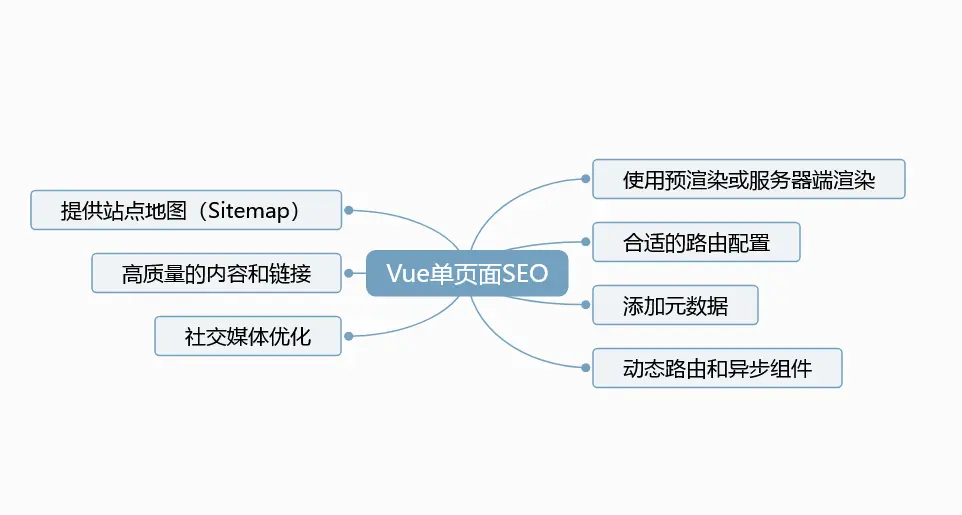
Vue单页面应用(SPA)怎么做SEO
在Vue单页面应用(SPA)中,由于内容的动态加载和路由切换,搜索引擎可能无法直接获取和索引页面的内容。不过,你可以采取一些策略来优化SEO,使你的Vue单页面应用在搜索引擎中更好地被索引和展示: 1:使用预渲染(Prerendering)或服务器端渲染(Server-Side Rendering,SS…...

简述【关系型数据库】
“关系型数据库”是博主在复习时做题遇到的知识点,用于简单扫盲 关系型数据库简称RDBMS,是依据关系模型来创建的数据库所谓“关系模型”就是“一对一、一对多、多对多”等关系模型。关系模型就是指二维表格模型,因而一个关系型数据库就是由二…...
LVS之DR模式(最常见的LVS负载方式,直接路由模式)
一、LVS-DR模式的数据流向 1、负载均衡器lvs调度器:只负责请求和转发到后端的真实服务器,但是响应结果,由后端服务器直接转发给客户端,不需要经过调度器的处理,减轻lvs调度器的负担,提高性能和稳定性 二、…...

006:vue使用lottie-web实现web动画
文章目录 1. 简介2. 优点3. 效果4. 安装使用5. lottie-web 常用方法6. Lottie-web 常用的事件 1. 简介 官方介绍:Lottie 是一个库,可以解析使用AE制作的动画(需要用bodymovie导出为json格式),支持web、ios、android、flutter和re…...
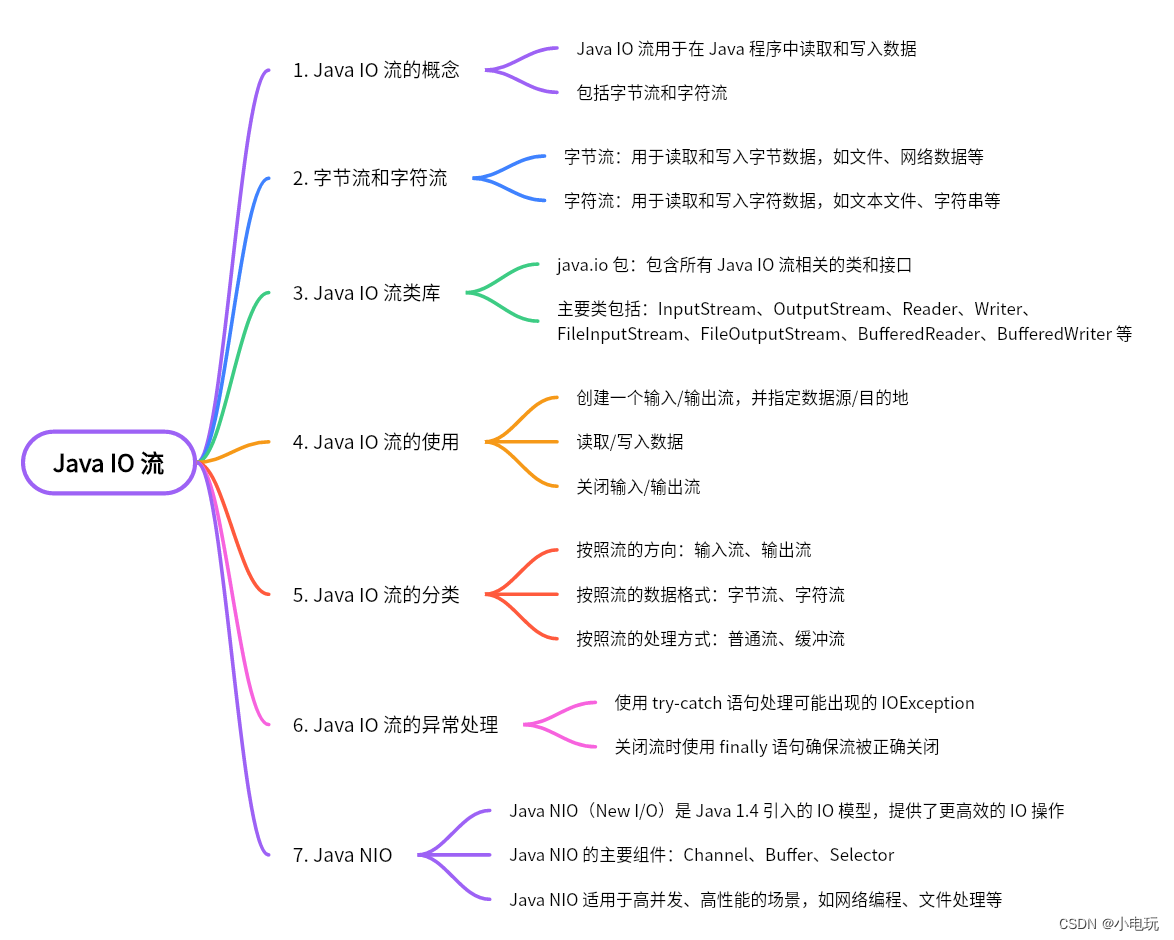
Java NIO
Java NIO 一,介绍 Java NIO(New IO)是 JDK 1.4 引入的一组新的 I/O API,用于支持非阻塞式 I/O 操作。相比传统的 Java IO API,NIO 提供了更快、更灵活的 I/O 操作方式,可以用于构建高性能网络应用程序。 …...

人机交互中的数字与文字
人机交互是指人类与计算机系统之间进行信息交流和操作的过程。在人机交互中,数字和文字被广泛应用于界面设计、输入输出、交流和信息展示等方面。 数字在人机交互中常用于表示数据、数量和参数等信息。通过数字,我们可以输入和输出各种数值,进…...
C++11新特性之十六:std::tie
在c 11标准库中,加入了std::tie,在c 14中改进,方便使用。 其与std::tuple关系密切, 主要目的是方便地使用std::tuple。 std::tie函数的作用就是从元素引用中生成一个std::tuple元组,其在头文件<tuple>中定义&…...
的感激之情)
今天是1024节日,作为一个程序员,我想表达我对Java和詹姆斯·高斯林(James Gosling)的感激之情
今天是1024节日 我感谢Java感谢詹姆斯高斯林 今天是1024节日,作为一个程序员,我想表达我对Java和詹姆斯高斯林(James Gosling)的感激之情。Java是一门伟大的编程语言,而詹姆斯高斯林是它的创造者之一。 首先…...

众和策略:华为汽车概念活跃,圣龙股份斩获12板,华峰超纤涨10%
华为轿车概念23日盘中再度生动,到发稿,华峰超纤涨超10%,佛山照明、圣龙股份、隆基机械、银宝山新等涨停,赛力斯涨近6%。 值得注意的是,圣龙股份已接连12个交易日涨停。 昨日晚间,圣龙股份宣布前三季度成果…...

关于一篇“范式详解”博文的批注
本篇文章是对于下面这个链接中的文章的批注。这篇文章详细讲述了第一、二、三范式和BCNF范式,希望我的这篇文章能帮助您更好的理解这篇优秀的博文 详解第一范式、第二范式、第三范式、BCNF范式-CSDN博客 “范式”批注 这样理解范式的概念:一张数据表的表…...

LNMP架构部署Discuz论坛系统
文章目录 LNMP架构&部署Discuz论坛系统部署LNMP架构环境前期准备安装Nginx安装mariadb安装php配置nginx 部署Discuz论坛系统下载Discuz论坛系统代码包部署Discuz论坛系统配置虚拟主机安装Discuz论坛访问站点尝试注册一个账号 LNMP架构&部署Discuz论坛系统 部署LNMP架构…...

【vscode】本地配置和根据不同项目不同的vscode配置
目录 1. .vscode项目配置2. vscode本地配置 1. .vscode项目配置 {"typescript.tsdk": "node_modules/typescript/lib","prettier.enable": false,"god.tsconfig": "./tsconfig.json",// TODO: 文件默认配置"[css]&quo…...

状态空间方程的离散化
一、理论基础 1、系统离散化(传递函数和状态空间方程) 【离散系统】传递函数和状态空间方程离散化-CSDN博客 状态空间方程的离散化 - 知乎 (zhihu.com) 2、差分方程的建立与分析 【精选】数学建模之差分方程模型详解_左手の明天的博客-CSDN博客 【信…...
【Docker从入门到入土 3】Docker镜像的创建方法
Part3 一、Docker镜像1.1 镜像的概念1.2 镜像结构的分层 二、Docker镜像的创建2.1 基于现有镜像创建2.1.1 创建思路2.1.2 举个例子 2.2 基于本地模板创建2.3 基于Dockerfile 创建 三、Dockerfile 详解3.1 Dockerfile 操作指令3.1.1 常用的操作指令3.1.2 CMD和ENTRYPOINT的区别…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
