【C++】二叉树进阶 -- 详解
一、二叉搜索树概念
二叉搜索树 又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

- 对二叉搜索树进行中序遍历,正好是一个升序序列。(左子树 -> 根 -> 右子树)
二、二叉搜索树操作
- 增删查的时间复杂度是:O(h)。h 是树的高度,最坏情况是 h 是 N。

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};1、二叉搜索树的查找
a、从 根 开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。b、 最多查找高度次 ,走到空,还没找到,这个值不存在。
2、二叉搜索树的插入
插入的具体过程如下:
- 树为空,则直接新增节点,赋值给 root 指针。
- 树不空,按二叉搜索树性质查找插入位置,插入新节点。

3、搜索二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回,否则要删除的结点可能分下面四种情况:
- 要删除的结点无孩子结点。
- 要删除的结点只有左孩子结点。
- 要删除的结点只有右孩子结点。
- 要删除的结点有左、右孩子结点。
看起来有待删除节点有 4 种情况,实际情况 a 可以与情况 b/c 合并起来,因此真正的删除过程如下:
- 情况 b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点 -- 直接删除。
- 情况 c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点 -- 直接删除。
- 情况 d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题 —— 替换法删除。

删除 3(删除的节点有两个孩子)替换法 -- 删除(以下两种方法任选一种)
- 左子树的最大节点 —— 2(左子树的最右节点)
- 右子树的最小节点 —— 4(右子树的最左节点)
- 替换节点赋值给删除节点后,删除替换节点。
- 替换节点要么没有孩子,要么只有一个孩子,可以直接删除。
三、二叉搜索树的实现
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key): _left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key){// 如果树为空,直接插入if (nullptr == _root){_root = new Node(key);return true;}// 按照二叉搜索树的性质查找key在树中的插入位置Node* cur = _root;// 记录cur的双亲,因为新元素最终插入在cur双亲左右孩子的位置Node* parent = nullptr;while (cur){parent = cur;if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;}// 插入元素cur = new Node(key);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;return true;}// 根据二叉搜索树的性质查找:找到值为key的节点在二叉搜索树中的位置bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){// 如果树为空,删除失败if (nullptr == _root)return false;// 查找在data在树中的位置Node* cur = _root;Node* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if(key > cur->_key){parent = cur;cur = cur->_right;}else{// 开始删除// 1、左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;cur = nullptr;}// 2、右为空else if (cur->_right == nullptr){if (_root == cur){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;cur = nullptr;}// 3、左右都不为空else{// 找到右子树最小节点进行替换Node* minParent = cur;Node* min = cur->_right;while (min->_left){minParent = min;min = min->_left;}swap(cur->_key, min->_key);if (minParent->_left == min)minParent->_left = min->_right;elseminParent->_right = min->_right;delete min;}return true;}}return false;}// key不在二叉搜索树中,无法删除if (nullptr == cur)return false;// 分以下情况进行删除if (nullptr == cur->_right){// 当前节点只有左孩子或者左孩子为空---可直接删除}else if (nullptr == cur->_right){// 当前节点只有右孩子---可直接删除}else{// 当前节点左右孩子都存在,直接删除不好删除,可以在其子树中找一个替代结点,比如:// 找其左子树中的最大节点,即左子树中最右侧的节点,或者在其右子树中最小的节点,即右子树中最小的节点// 替代节点找到后,将替代节点中的值交给待删除节点,转换成删除替代节点}return true;}void InOrder(){_InOrder(_root);cout << endl;}bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}~BSTree(){_Destory(_root);}BSTree() = default;BSTree(const BSTree<K>& t){_root = _Copy(t._root);}// t2 = t1BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}private:Node* _Copy(Node* root){if (root == nullptr){return nullptr;}Node* copyRoot = new Node(root->_key);copyRoot->_left = _Copy(root->_left);copyRoot->_right = _Copy(root->_right);return copyRoot;}void _Destory(Node*& root){if (root == nullptr){return;}_Destory(root->_left);_Destory(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{// 找右树的最左节点替换删除Node* min = root->_right;while (min->_left){min = min->_left;}swap(root->_key, min->_key);//return Erase(key); // 错误 - 找到的不是我们要的位置return _EraseR(root->_right, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key < key)return _FindR(root->_right, key);else if (root->_key > key)return _FindR(root->_left, key);elsereturn true;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;
};四、二叉搜索树的应用
1、 K模型(判断关键字在不在) :K 模型即只有 key 作为关键码,结构中只需要存储 Key 即可,关键码即为需要搜索到 的值。比如:给一个单词 word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为 key,构建一棵二叉搜索树。
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2、 KV模型 :每一个关键码 key,都有与之对应的值 Value,即 <Key, Value> 的键值对。该种方式在现实生活中非常常见:比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文 <word, chinese> 就构成一种键值对;再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是 <word, count> 就构成一种键值对。
// 改造二叉搜索树为KV结构
template<class K, class V>
struct BSTreeNode
{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _valueBSTreeNode(const K& key, const V& value): _left(nullptr), _right(nullptr), _key(key), _Value(value){}
};template<class K, class V>
class BSTree
{typedef BSTNode<K, V> Node;
public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){//...return true;}void InOrder(){_InOrder(_root);cout << endl;}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}
private:Node* _root = nullptr;
};void TestBSTree1()
{// 输入单词,查找单词对应的中文翻译BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("tree", "树");dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("sort", "排序");// 插入词库中所有单词string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret){cout << "对应的中文:" << ret->_value << endl;}else{cout << "没有此单词" << endl;}}
}void TestBSTree2()
{// 统计水果出现的次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在,说明水果第一次出现,则插入<水果, 1>// 2、在,则查找到的节点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret){ret->_value++;}else{countTree.Insert(str, 1);}}countTree.InOrder();
}五、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
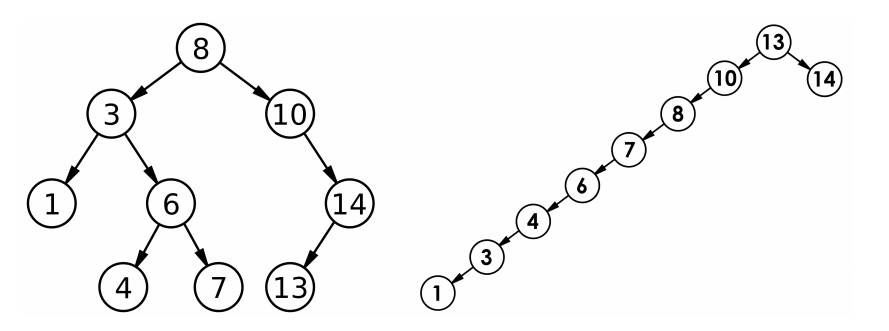
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: logN。
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N。
如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?那么我们后面将学习的 AVL 树和红黑树 就可以派上用场了。
相关文章:

【C++】二叉树进阶 -- 详解
一、二叉搜索树概念 二叉搜索树 又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右子树不为空,则右子树上所有节点的值都大于根节点…...

K8S集群中Node节点资源不足导致Pod无法运行的故障排查思路
K8S集群中Node节点资源不足导致Pod无法运行的故障排查思路 Node节点资源不足可能会产生的故障 故障一:Pod数量太多超出物理节点的限制每一台Node节点中默认限制最多运行110个Pod资源,当一个应用程序有成百上千的Pod资源时,如果不扩容Node节…...
Node.js与npm版本比对
Node.js与npm版本比对 Node.js与npm版本比对版本对比表Node版本对比 Node.js与npm版本比对 我们在项目开发过程中,经常会遇到公司一些老的前端工程项目,而我们当前的node及npm版本都是相对比较新的了。 在运行以前工程时,会遇到相关环境不匹…...

智加科技与东风柳汽达成深度合作 自动驾驶重卡计划2024年初量产交付
(2023年10月19日,苏州)全球领先的重卡自动驾驶技术公司智加科技与东风柳汽宣布,双方共同开发的自动驾驶重卡H7计划2024年初实现量产交付。未来,双方将携手推出安全可靠、高性价比、性能卓越的自动驾驶重卡产品…...

mac下配置环境-node以及nvm
当前配置环境主要针对于mac下系统,需要提前安装brew包 如需要配置,可查阅:Brew包的基本安装(手把手教学)-CSDN博客 如果是window环境配置,分享一个不错的帖子:nvm的安装和使用(详细&…...
:es创建映射和设置)
Elasticsearch基础篇(六):es创建映射和设置
es创建映射和设置 一、什么是 Elasticsearch 映射?二、映射中的字段类型常见字段类型 (Common data types)对象和关联类型(Objects and relational types)结构化数据类型(Structured data types)…...
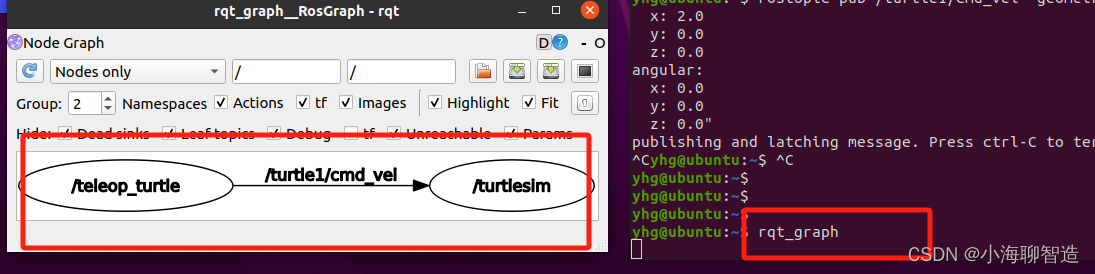
机器人系统 ROS 常用命令行工具
1. 启动ros 主节点 roscore roscore运行成功如图: 1.1 rosrun 启动服务节点 例子:启动一个小乌龟节点 rosrun turtlesim turtlesim_node运行结果如图: 1.2 启动键盘控制 打开新的命令窗口,启动turtle_teleop_key 节点 rosr…...

Jasypt加解密、信息脱敏
文章目录 一、介绍二、Spring集成1、 Maven依赖2、application.xml的配置3、配置文件使用4、方法加密 二、SpringBoot集成1、 Maven依赖2、 Java Bean配置jasyptStringEncryptor3、配置文件使用4、Bean使用加密字段自动解密 一、介绍 Jasypt is a java library which allows th…...
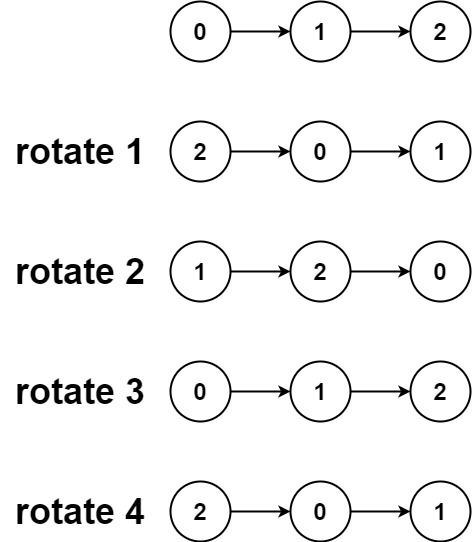
力扣每日一题61:旋转链表
题目描述: 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 示例 1: 输入:head [1,2,3,4,5], k 2 输出:[4,5,1,2,3]示例 2: 输入:head [0,1,2], k 4 输…...
SSM - Springboot - MyBatis-Plus 全栈体系(三十六)
第八章 项目实战 四、后台功能开发 3. 头条模块开发 3.1 登陆验证和保护 3.1.1 需求描述 客户端在进入发布页前、发布新闻前、进入修改页前、修改前、删除新闻前先向服务端发送请求携带 token 请求头后端接收 token 请求头后,校验用户登录是否过期并做响应前端根…...

作为开发的我能力模型图是什么样子的,应该如何去绘制?
作为开发的我能力模型图是什么样子的,应该如何去绘制? 能力模型图是一种用来描述个人或职位所需技能和能力的工具,对于开发人员来说,能力模型图通常包括技术能力、软技能和专业知识等多个维度。下面是一种可能的构建和绘制开发人员…...

【会议征稿通知】第三届密码学、网络安全和通信技术国际会议(CNSCT 2024)
第三届密码学、网络安全和通信技术国际会议(CNSCT 2024) 2024 3rd International Conference on Cryptography, Network Security and Communication Technology 随着互联网和网络应用的不断发展,网络安全在计算机科学中的地位越来越重要&…...

Python学习笔记——MYSQL,SQL核心
食用说明:本笔记适用于有一定编程基础的伙伴们。希望有助于各位! SQL语言分类 SQL注释 库管理 表管理 数据操作 分组聚合 分页限制 需要注意的是关键字的顺序不可以错乱,否则会报错其中LIMIT关键字的n是指从第n个开始,m是指查…...

集成学习方法之随机森林-入门
1、 什么是集成学习方法 集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测。 2、 什么是随机森林 在机器学习中&…...

blender怎么在一个面上对半切割(不影响别的面)
1进入编辑模式 2.在面选择模式下,选中该物体需要切割成两半的面。 3.按K这个快捷键(切记,必须得用快捷键,不用的话没办法调出第一个绿色切割点),将切割点移动到需要切割的起始边,按住Shift键不放…...
vue3中使用vue3-pdf-app和使用浏览器内置的PDF插件浏览器PDF文件
文章目录 先准备一个PDF使用浏览器内置的PDF插件预览PDF在HTML中使用浏览器插件预览PDFVscode使用插件发布服务后直接通过URL地址访问PDF可使用的浏览器 在vue3项目中预览PDF文件vue3项目也是可以通过URL地址访问文件的vue3中使用浏览器内置的PDF插件预览PDF代码如下所示&#…...

fastadmin 后台添加视频
做个记录,字段自行对照解决 1.add.html <div class"form-group"><label class"control-label col-xs-12 col-sm-2">{:__(Video)}:</label><div class"col-xs-12 col-sm-8"><div class"input-group">&l…...
)
TFHE 的全同态模结构(FHE Module Structure)
参考文献: [CGGI20] Chillotti I, Gama N, Georgieva M, et al. TFHE: fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.[BGGJ20] Boura C, Gama N, Georgieva M, et al. Chimera: Combining ring-lwe-based ful…...

rapidocr_paddle[gpu]:GPU端推理库来了
简介 rapidocr_paddle系列包是基于PaddlePaddle框架作为推理引擎的,支持CPU和GPU上推理。值得说明的是,这个包和PaddleOCR相比,代码基本都是一样的,只不过这个库将里面核心推理代码抽了出来,更加精简而已。 推荐GPU上…...
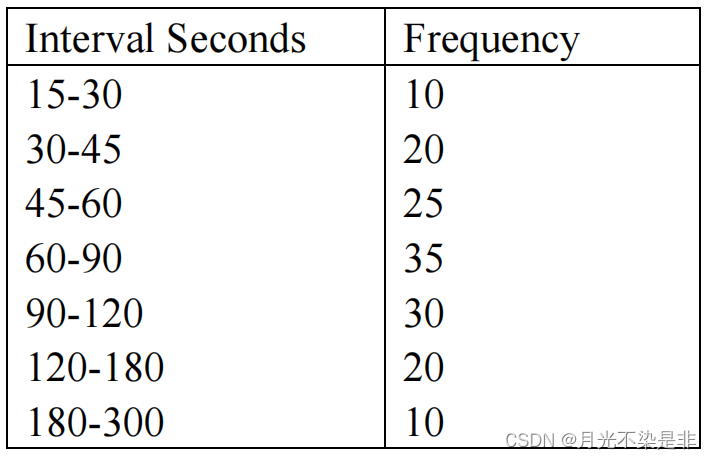
PKU 概率论+数理统计+建模 期中考复习总结
目录 计算条件概率计算概率(放回与不放回)生成随机数算法Linear Congruential Method判断是否是full period Uniformity (test of frequency)1.Chi-Square testmethodreminderexample 2.Kolmogorov-Sminov testmethodexample Independence (test of auto…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
