二叉树进阶

欢迎来到Cefler的博客😁
🕌博客主页:那个传说中的man的主页
🏠个人专栏:题目解析
🌎推荐文章:题目大解析(3)

目录
- 👉🏻二叉搜索树
- 概念
- 👉🏻二叉搜索树模拟实现
- Insert插入
- find查找
- 中序遍历
- Erase删除
- InsertR递归插入
- FindR递归查找
- EraseR递归删除
- 🍒BinarySearchTree.h
👉🏻二叉搜索树
概念
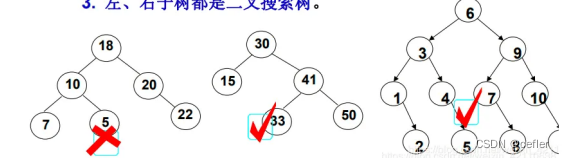
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
即:左<根<右
👉🏻二叉搜索树模拟实现
Insert插入
bool Insert(const K& key){if (_root == nullptr)//如果为空直接创建新结点{_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (cur)//key比当前cur结点的key值小往左边走,大则往右边走,直到遇到空{parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);//此时遇到空要创建新结点//但此时我们还要记得将其与parent连接起来,至于是在parent的左边还是右边,看比大小if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}
过程即为:小于往左走,大于往右走,遇到空创建新结点,进行连接父节点
find查找
bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn true;//相等说明找到,返回true}return false;}
中序遍历
void _InOrder(Node* root)//中序遍历{if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}void InOrder()//套一层{_InOrder(_root);cout << endl;}
Erase删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情
况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
而a情况可以归属于b和c任意一个情况,a情况当把结点删除后,父节点想向指向左右哪边都行,反正都为空无所谓。
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点
中,再来处理该结点的删除问题–替换法删除
替换法删除:
1.要么从左子树中找到最大结点来替换
2.要么从右子树找到最小结点来替换
所以现在梳理一下代码思路:
1.先找到要删除的结点位置,能找到再删除,找不到返回false
2.开始删除,判情况(b,c,d),对症下药
代码如下:
bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur)//寻找要删除的结点{ if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//找到了就可以开始删除了,但是要判情况,对症下药if (cur->_left == nullptr){//左边为空,则删除后,将父节点连接cur的右边if (cur == _root)//如果要删除的结点就是初始根结点{_root = cur->_right;}//先确定此时cur在父节点的左边还是右边if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}else if (cur->_right == nullptr){//右边为空if (cur == _root)//如果要删除的结点就是初始根结点{_root = cur->_left;}if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}else{//左右都不为空,此时用替换法//这里我们以寻找右边树最小值的替换法执行;而右边树最小值即可以认为就是右边树最左边结点Node* parent = cur;Node* subleft = cur->_right;while (subleft->_left)//当左边遇到空,说明此时subleft已经遍历到最左边{parent = subleft;subleft = subleft->_left;}//找到后,可以进行交换了swap(cur->_key, subleft->_key);//现在进行删除,而且删除情况属于a情况if (subleft == parent->_left){parent->_left = subleft->_right;//这边=subleft->_right或者subleft->_left都可以}else{parent->_right = subleft->_right;}}return true;}}return false;}
InsertR递归插入
bool _InsertR(Node*& root, const K& key)//递归插入{if (root == nullptr){root = new Node(key);//传引用的好处就是此时的root就是其父节点的左/右节点,无需记录父节点return true;}if (root->_key > key){_InsertR(root->_left, key);}else if (root->_key < key){_InsertR(root->_right, key);}elsereturn false;}
FindR递归查找
bool _FindR(Node* root, const K& key)//递归查找{if (root == nullptr)return false;if (root->_key > key){FindR(root->_left, key);}else if (root->_key < key){FindR(root->_right, key);}elsereturn true;}
EraseR递归删除
bool _EraseR(Node*& root, const K& key)//这里我们仍然用引用root,这样连接时就不用记录父节点了{if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{//开始删除if (root->_left == nullptr){//左为空root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{//左右都不为空//这里以寻找右子树最小值Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);// 转换成在子树去递归删除return _EraseR(root->_right, key);}}}
🍒BinarySearchTree.h
#pragma once
#include <iostream>
using namespace std;
template <class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};
template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Insert(const K& key){if (_root == nullptr)//如果为空直接创建新结点{_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (cur)//key比当前cur结点的key值小往左边走,大则往右边走,直到遇到空{parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);//此时遇到空要创建新结点//但此时我们还要记得将其与parent连接起来,至于是在parent的左边还是右边,看比大小if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn true;//相等说明找到,返回true}return false;}bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur)//寻找要删除的结点{ if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//找到了就可以开始删除了,但是要判情况,对症下药if (cur->_left == nullptr){//左边为空,则删除后,将父节点连接cur的右边if (cur == _root)//如果要删除的结点就是初始根结点{_root = cur->_right;}//先确定此时cur在父节点的左边还是右边if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}else if (cur->_right == nullptr){//右边为空if (cur == _root)//如果要删除的结点就是初始根结点{_root = cur->_left;}if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}else{//左右都不为空,此时用替换法//这里我们以寻找右边树最小值的替换法执行;而右边树最小值即可以认为就是右边树最左边结点Node* parent = cur;Node* subleft = cur->_right;while (subleft->_left)//当左边遇到空,说明此时subleft已经遍历到最左边{parent = subleft;subleft = subleft->_left;}//找到后,可以进行交换了swap(cur->_key, subleft->_key);//现在进行删除,而且删除情况属于a情况if (subleft == parent->_left){parent->_left = subleft->_right;//这边=subleft->_right或者subleft->_left都可以}else{parent->_right = subleft->_right;}}return true;}}return false;}void InOrder()//套一层{_InOrder(_root);cout << endl;}bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root,key);}bool EraseR(const K& key){return _EraseR(_root, key);}
private:bool _EraseR(Node*& root, const K& key)//这里我们仍然用引用root,这样连接时就不用记录父节点了{if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{//开始删除if (root->_left == nullptr){//左为空root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{//左右都不为空//这里以寻找右子树最小值Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);// 转换成在子树去递归删除return _EraseR(root->_right, key);//root->_right或者root->_left都可以,反正都是空}}}bool _InsertR(Node*& root, const K& key)//递归插入{if (root == nullptr){root = new Node(key);//传引用的好处就是此时的root就是其父节点的左/右节点,无需记录父节点return true;}if (root->_key > key){_InsertR(root->_left, key);}else if (root->_key < key){_InsertR(root->_right, key);}elsereturn false;}bool _FindR(Node* root, const K& key)//递归查找{if (root == nullptr)return false;if (root->_key > key){FindR(root->_left, key);}else if (root->_key < key){FindR(root->_right, key);}elsereturn true;}void _InOrder(Node* root)//中序遍历{if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;
};
如上便是本期的所有内容了,如果喜欢并觉得有帮助的话,希望可以博个点赞+收藏+关注🌹🌹🌹❤️ 🧡 💛,学海无涯苦作舟,愿与君一起共勉成长

相关文章:
二叉树进阶
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 目录 👉🏻二叉搜索树概念 Ǵ…...
前端性能优化 - 虚拟滚动
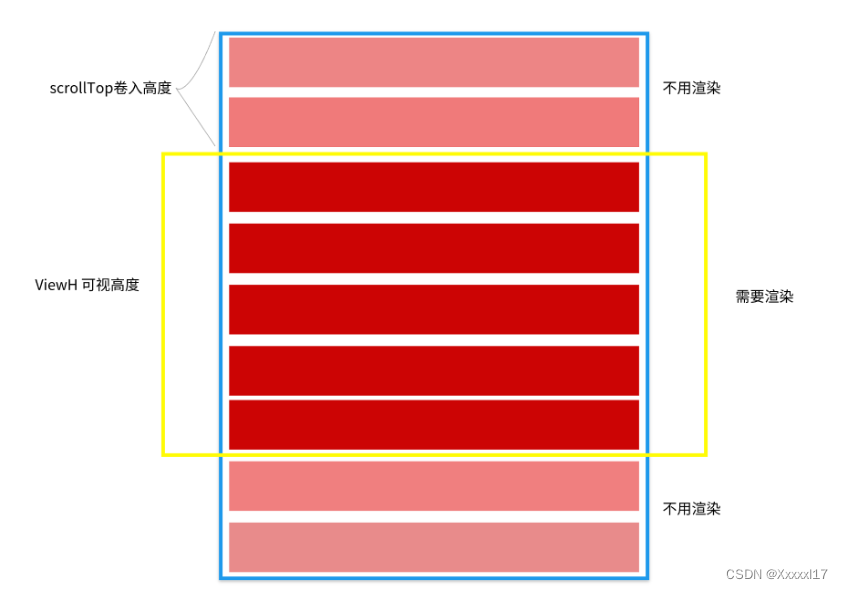
一 需求背景 需求:在一个表格里面一次性渲染全部数据,不采用分页形式,每行数据都有Echart图插入。 问题:图表渲染卡顿 技术栈:Vue、Element UI 卡顿原因:页面渲染时大量的元素参与到了重排的动作中&#x…...
手写 Promise(1)核心功能的实现
一:什么是 Promise Promise 是异步编程的一种解决方案,其实是一个构造函数,自己身上有all、reject、resolve这几个方法,原型上有then、catch等方法。 Promise对象有以下两个特点。 (1)对象的状态不受…...

深入探究Java内存模型
文章目录 🌟 Java虚拟机内存模型🍊 一、方法区🍊 二、堆🎉 堆的基本概念🎉 堆的结构📝 新生代📝 老年代 🎉 堆的分配策略📝 对象优先分配📝 空间优先分配 &am…...

深度学习 | Pytorch深度学习实践 (Chapter 10、11 CNN)
十、CNN 卷积神经网络 基础篇 首先引入 —— 二维卷积:卷积层保留原空间信息关键:判断输入输出的维度大小特征提取:卷积层、下采样分类器:全连接 引例:RGB图像(栅格图像) 首先,老师…...
谈谈你对spring boot 3.0的理解
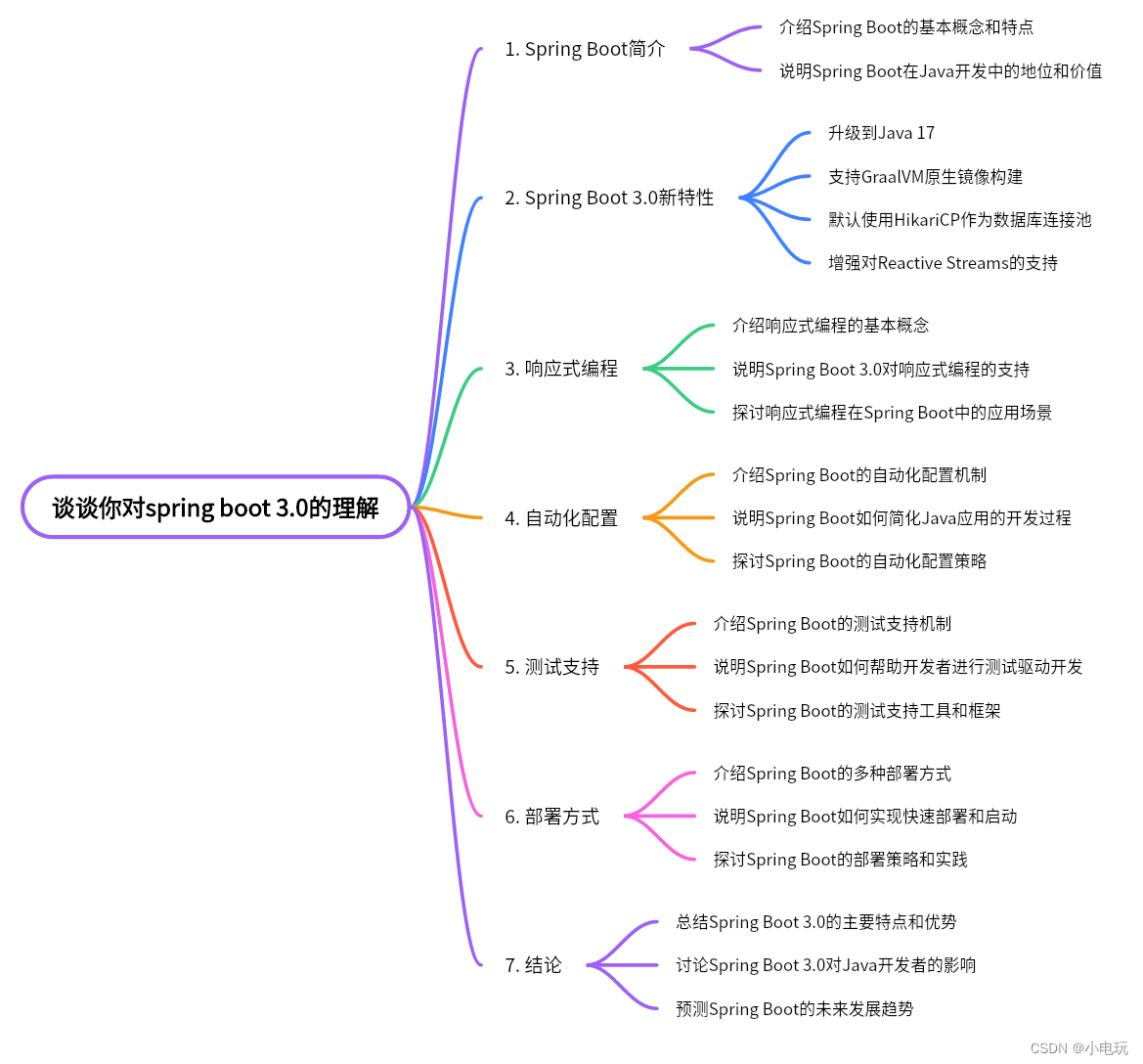
谈谈你对spring boot 3.0的理解 一,Spring Boot 3.0 的兼容性 Spring Boot 3.0 在兼容性方面做出了很大的努力,以支持存量项目和老项目。尽管如此,仍需注意以下几点: Java 版本要求:Spring Boot 3.0 要求使用 Java 1…...
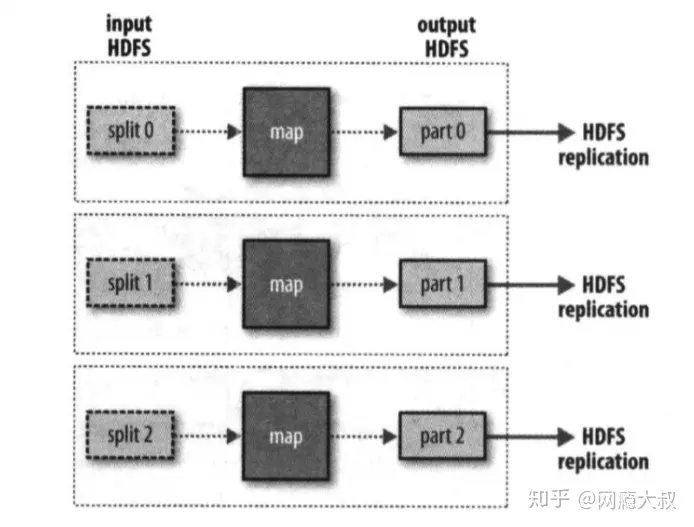
【大数据】Hadoop
文章目录 概述Hadoop组成HDFSMapReduce写MapReduce程序(Hadoop streaming) YARNHadoop 启动 工作方式Hadoop的主从工作方式Hadoop的守护进程 运行模式本地运行模式伪分布式运行模式完全分布式运行模式 Hadoop高可用的解决方案ZooKeeper quorumZKFC 环境搭…...
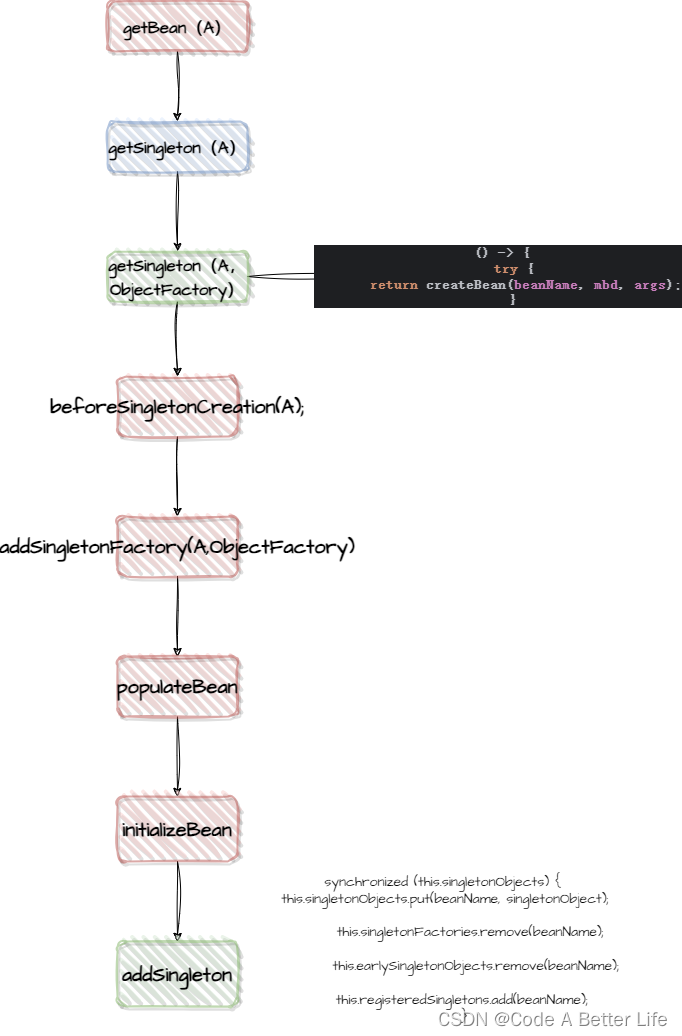
Spring实例化源码解析之Bean的实例化(十二)
前言 本章开始分析finishBeanFactoryInitialization(beanFactory)方法,直译过来就是完成Bean工厂的初始化,这中间就是非lazy单例Bean的实例化流程。ConversionService在第十章已经提前分析了。重点就是最后一句,我们的bean实例化分析就从这里…...

git常用的几条命令介绍
必须了解的命令整理 1,git init 初始化一个新的Git仓库。 这将在当前目录中创建一个名为".git"的子目录,Git会将所有仓库的元数据存储在其中。 2,git clone 克隆一个已存在的仓库。 这会创建一个本地仓库的副本,包…...

使用VisualSVN在Windows系统上设置SVN服务器,并结合内网穿透实现公网访问
文章目录 前言1. VisualSVN安装与配置2. VisualSVN Server管理界面配置3. 安装cpolar内网穿透3.1 注册账号3.2 下载cpolar客户端3.3 登录cpolar web ui管理界面3.4 创建公网地址 4. 固定公网地址访问 前言 SVN 是 subversion 的缩写,是一个开放源代码的版本控制系统…...
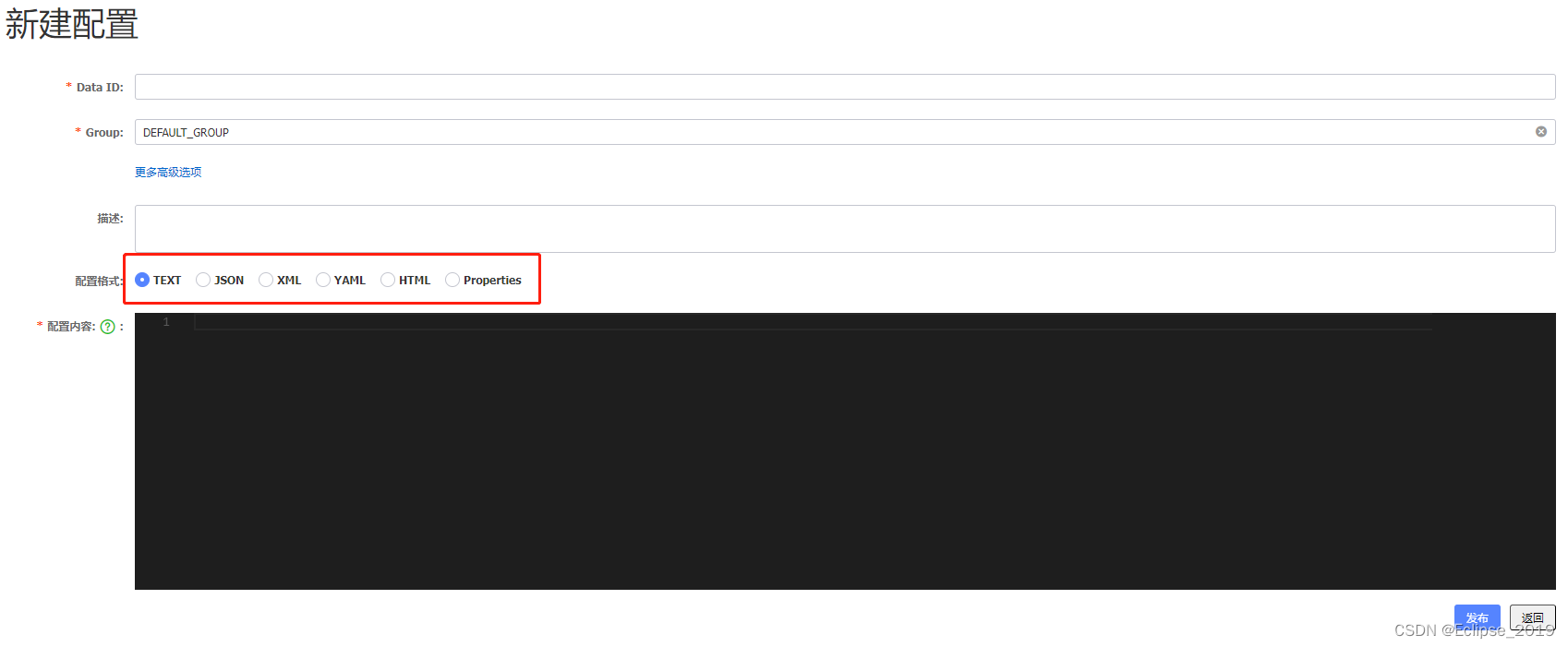
第18章 SpringCloud生态(三)
18.21 Nacos能存储什么样格式的数据(配置中心) 难度:★ 重点:★ 白话解析 看下面这副Nacos控制台的截图就明白了 参考答案 六种格式数据:Text、JSON、XML、Yaml、HTML和Properties格式。 18.22 Nacos是如何实现配置动态更新的(配置中心) 难度:★★ 重点:★★★ 白话…...
leetcode:2347. 最好的扑克手牌(python3解法)
难度:简单 给你一个整数数组 ranks 和一个字符数组 suit 。你有 5 张扑克牌,第 i 张牌大小为 ranks[i] ,花色为 suits[i] 。 下述是从好到坏你可能持有的 手牌类型 : "Flush":同花,五张相同花色的…...
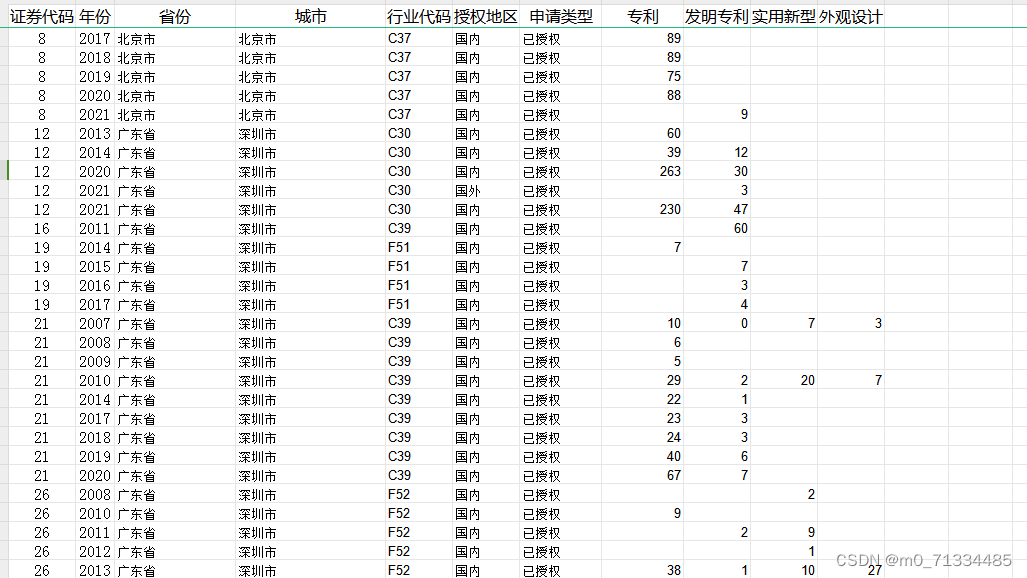
2007-2022 年上市公司国内外专利授权情况数据
2007-2022 年上市公司国内外专利授权情况 1、来源:国家知识产权局 2、时间:2007-2022 年 3、范围:上市公司 4、指标: 证券代码、年份、省份、城市、行业代码、授权地区、申请类型、专利、发明专利、实用新型、外观设计 5、…...

安全渗透测试网络基础知识之路由技术
#1.静态路由技术 ##1.1路由技术种类: 静态路由技术、动态路由技术 ##1.2静态路由原理 静态路由是网络中一种手动配置的路由方式,用于指定数据包在网络中的传输路径。与动态路由协议不同,静态路由需要管理员手动配置路由表,指定目的网络和下一跳路由器的关联关系。 比较适合…...
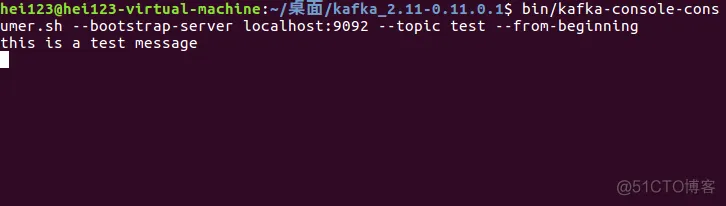
【大数据】Kafka 实战教程(二)
Kafka 实战教程(二) 1.下载2.安装3.配置4.运行4.1 启动 Zookeeper4.2 启动 Kafka 5.第一个消息5.1 创建一个 Topic5.2 创建一个消息消费者5.3 创建一个消息生产者 1.下载 你可以在 Kafka 官网:http://kafka.apache.org/downloads,…...
React 框架
1、React 框架简介 1.1、介绍 CS 与 BS结合:像 React,Vue 此类框架,转移了部分服务器的功能到客户端。将CS 和 BS 加以结合。客户端只用请求一次服务器,服务器就将所有js代码返回给客户端,所有交互类操作都不再依赖服…...

数据结构与算法之图: Leetcode 133. 克隆图 (Typescript版)
克隆图 https://leetcode.cn/problems/clone-graph/description/ 描述 给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。 图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[No…...

illuminate/database 使用 一
illuminate/database 是完整的php数据库工具包,即ORM(Object-Relational Mapping)类库。 提供丰富的查询构造器,和多个驱动的服务。作为Laravel的数据库层使用,也可以单独使用。 一 使用 加载composer之后ÿ…...
前端koa搭建服务器(保姆级教程)——part1
目录 koa简介前端项目搭建koa环境第一步:新建项目第二步:环境初始化,安装依赖初始化项目,生成package.json文件安装koa依赖安装koa-router 路由管理依赖安装dotenv 环境变量依赖安装nodemon 热启动依赖 第三步:代码调用…...

js逆向第一课 密码学介绍
什么是密码学? 密码学(Cryptology)是一种用来混淆的技术,它希望将正常的、可识别的信息转变为无法识别的信息。 目前密码学的研究,一种是偏应用,把现有的,别人研究出来的密码学算法,放在一个合…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
