[补题记录] Atcoder Beginner Contest 325(E、F)
URL:https://atcoder.jp/contests/abc325

目录
E
Problem/题意
Thought/思路
Code/代码
F
Problem/题意
Thought/思路
Code/代码
E
Problem/题意
有一个二维矩阵,D[i][j] 表示从 i 到 j 的距离。从 i 到 j 有两种方式:
- 坐汽车:耗费 D[i][j] * A;
- 坐火车:耗费 D[i][j] * B + C;
你可以选择在某个城市 i 换乘火车,但不能再从火车换乘汽车。问最少的时间。
Thought/思路
恼馋题目,使我的 rank 旋转。
![]()
最重要的是理解这句话,然后做两个反向的最短🦌即可。
Code/代码
#include "bits/stdc++.h"#define int long longconst int inf = 1e15;int n, a, b, c, d[1007][1007], dis1[1000007], dis2[1000007];void dij(int s, int* dis) {for (int i = 1; i <= 1000000; ++ i) dis[i] = inf;dis[s] = 0;std::queue <int> q;q.push(s);while (!q.empty()) {int i = q.front(); q.pop();for (int j = 1; j <= n; ++ j) {int w = (s == 1 ? d[i][j] * a : d[i][j] * b + c);if (dis[j] > w + dis[i]) {dis[j] = w + dis[i];q.push(j);}}}
}signed main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);std::cin >> n >> a >> b >> c;for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= n; ++ j) {std::cin >> d[i][j];}}dij(1, dis1);dij(n, dis2);int ans = inf;for (int i = 1; i <= n; ++ i){ans = std::min(dis1[i] + dis2[i], ans);}std::cout << ans;}F
Problem/题意
有 N 条传输带需要监控,每条传输带长度为 D[i],现在有两种监控可以选择:
- 第一种:监控长度为 L[1],售价 C[1];
- 第二种:监控长度为 L[2],售价 C[2];
要求:
- 对于传输带 D[i],所选的监控可以覆盖其长度;
- 每种监控的购买数量不能超过 K[1]、K[2];
问是否能保证 N 条传输带都能被完整监控,若能,最小代价是多少。
Thought/思路
这个题要求维护最小值以及类似背包的最大数量。
通常我们在背包中,dp 表示最大价值,但在这个题中,多了一个 K 需要维护。
再想到,如果知道了某个状态下的 K[1]、K[2],其实就能求出这个状态下的价值。
因此,我们可以把 K2 当作 dp 表示的值,维护 K1 不超过限制的情况下,K2 的最少数量。
因此,dp[i][j] 表示:前 i 个,一共使用了 j 个一类监控,所需要的最少二类监控的数量。
Code/代码
#include "bits/stdc++.h"#define int long longconst int inf = 1e15;int n, d[100007], dp[107][1007];
std::array <int, 3> l, c, k;signed main() {std::cin >> n;for (int i = 1; i <= n; ++ i) {std::cin >> d[i];for (int j = 0; j <= 1000; ++ j) {dp[i][j] = inf;}}std::cin >> l[1] >> c[1] >> k[1];std::cin >> l[2] >> c[2] >> k[2];for (int i = 1; i <= n; ++ i) {for (int j = 0; j <= k[1]; ++ j) { // 总共用了 j 个 K1for (int k = 0; k <= j; ++ k) { // j 与 k 做差,得出第 i 个用了几个 K1int p = j - k;int a = (d[i] - p * l[1] <= 0 ? 0 : d[i] - p * l[1]);dp[i][j] = std::min(dp[i][j], dp[i - 1][k] + (a % l[2] == 0 ? a / l[2] : a / l[2] + 1));}}}int ans = inf;for (int i = 0; i <= k[1]; ++ i) {if (dp[n][i] <= k[2]) {ans = std::min(i * c[1] + dp[n][i] * c[2], ans);}}if (ans == inf) std::cout << -1;else std::cout << ans;
}相关文章:

[补题记录] Atcoder Beginner Contest 325(E、F)
URL:https://atcoder.jp/contests/abc325 目录 E Problem/题意 Thought/思路 Code/代码 F Problem/题意 Thought/思路 Code/代码 E Problem/题意 有一个二维矩阵,D[i][j] 表示从 i 到 j 的距离。从 i 到 j 有两种方式: 坐汽车&…...

1024啊啊啊啊啊啊
1024 程序员节快乐,没什么想发的,只是想要个1024胸章。...

淘宝商品详情API接口(H5端和APP端),淘宝详情页,商品属性接口,商品信息查询
一、接口参数说明:提取淘宝商品详情页各项数据,包含skuid、价格、收藏数、加购数、月销售量、主图、标题、详情页图片等页面上可以看奥的数据都可以拿到。 点击获取key和secret 二、使用场景 1、商品销售情况分析,根据销量调整活动方案&am…...
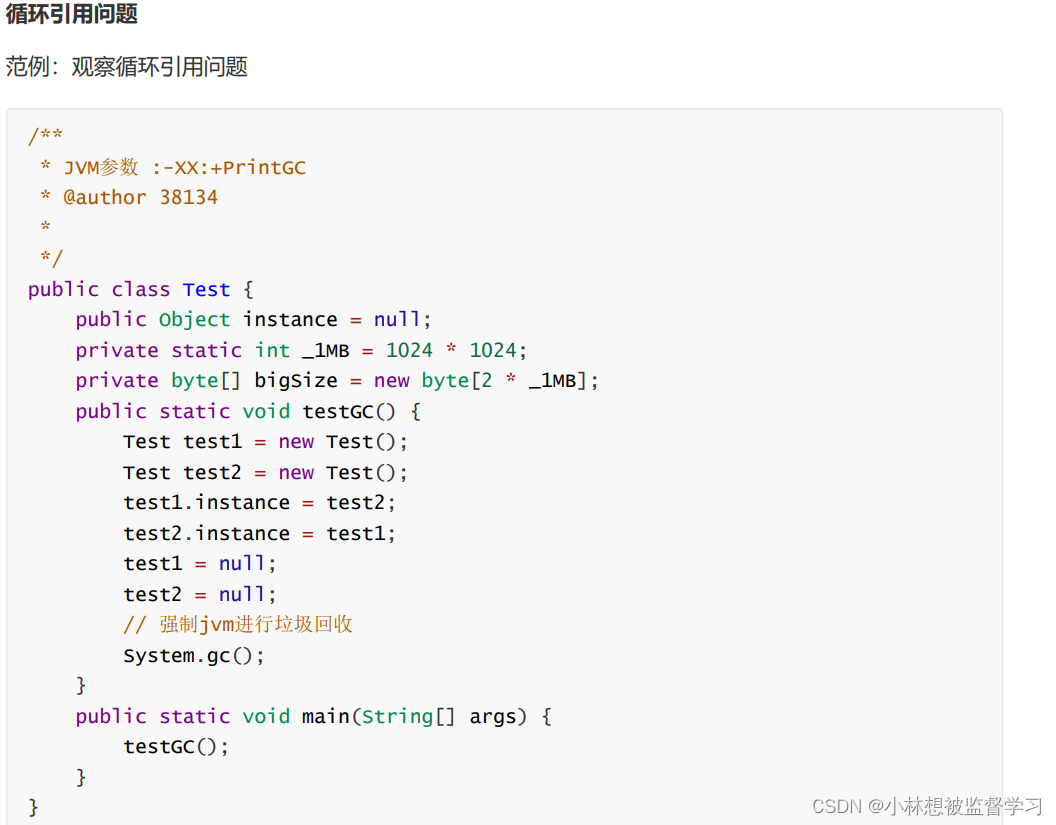
JVM的几个面试重点
JVM的内存区域划分 JVM类加载机制 前言 Java程序最开始是一个 .java 的文件,JVM把它编译成 .closs 文件(字节码文件),运行 Java 程序, JVM 就会读取 .class 文件,把文件内容读取到内存中,构造出…...
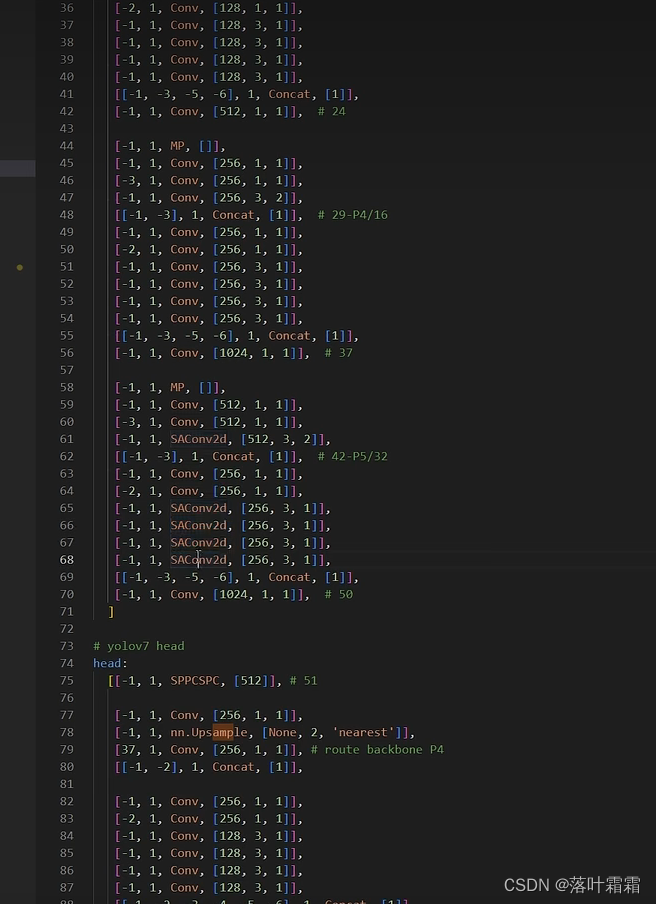
[yolo系列:YOLOV7改进-添加CoordConv,SAConv.]
文章目录 概要CoordConvSAConv 概要 CoordConv(Coordinate Convolution)和SAConv(Spatial Attention Convolution)是两种用于神经网络中的特殊卷积操作,用于处理图像数据或其他多维数据。以下是它们的简要介绍&#x…...
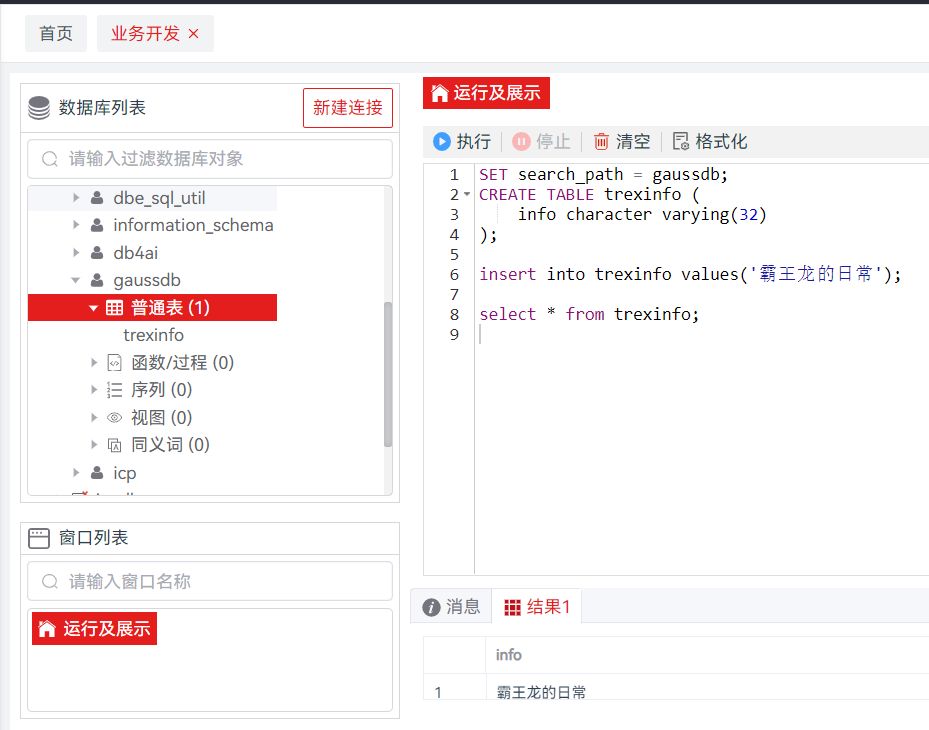
【万字实操】可视化运维平台openGauss Datakit,带你轻松玩转openGauss 5.0
openGauss Datakit:openGauss社区推出的可视化的运维工具. 特性优势 初级用户学习openGauss门槛高让你望而却步?openGauss Datakit一键化安装企业版集群、监控、日志分析、SQL诊断,让你快速上手,快速部署,从容面对企业环境&#…...

《动手学深度学习 Pytorch版》 10.1 注意力提示
10.1.1 生物学中的注意力提示 “美国心理学之父” 威廉詹姆斯提出的双组件(two-component)框架: 非自主性提示:基于环境中物体的突出性和易见性 自主性提示:受到了认知和意识的控制 10.1.2 查询、键和值 注意力机制…...

C# 写入文件比较
数据长度:128188个long BinaryWriter每次写一个long 耗时14.7828ms StreamWriter每次写一个long 耗时44.0934 ms FileStream每次写一个long 耗时20.5142 ms FileStream固定chunk写入,循环操作数组,耗时13.4126 ms byte[] chunk new byte[d…...
rust解法)
医院设备利用(Use of Hospital Facilities, ACM/ICPC World Finals 1991, UVa212)rust解法
医院里有n(n≤10)个手术室和m(m≤30)个恢复室。每个病人首先会被分配到一个手术室,手术后会被分配到一个恢复室。从任意手术室到任意恢复室的时间均为t1,准备一个手术室和恢复室的时间分别为t2和t3…...

解决github ping不通的问题(1024程序员节快乐!
1024程序员节快乐!(随便粘贴一个文档,参加活动 解决github ping不通的问题 域名解析(域名->IP):https://www.ipaddress.com/ Ubuntu平台 github经常ping不通或者访问缓慢,方法是更改host…...
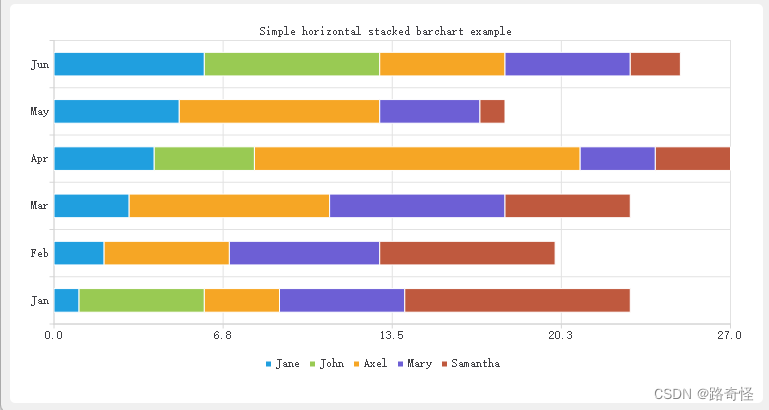
QT基础 柱状图
目录 1.QBarSeries 2.QHorizontalBarSeries 3.QPercentBarSeries 4.QHorizontalPercentBarSeries 5.QStackedBarSeries 6.QHorizontalStackedBarSeries 从上图得知柱状的基类是QAbstractBarSeries,派生出来分别是柱状图的水平和垂直类,只是类型…...

微机原理与接口技术-第七章输入输出接口
文章目录 I/O接口概述I/O接口的典型结构基本功能 I/O端口的编址独立编址统一编址 输入输出指令I/O寻址方式I/O数据传输量I/O保护 16位DOS应用程序DOS平台的源程序框架DOS功能调用 无条件传送和查询传送无条件传送三态缓冲器锁存器接口电路 查询传送查询输入端口查询输出端口 中…...
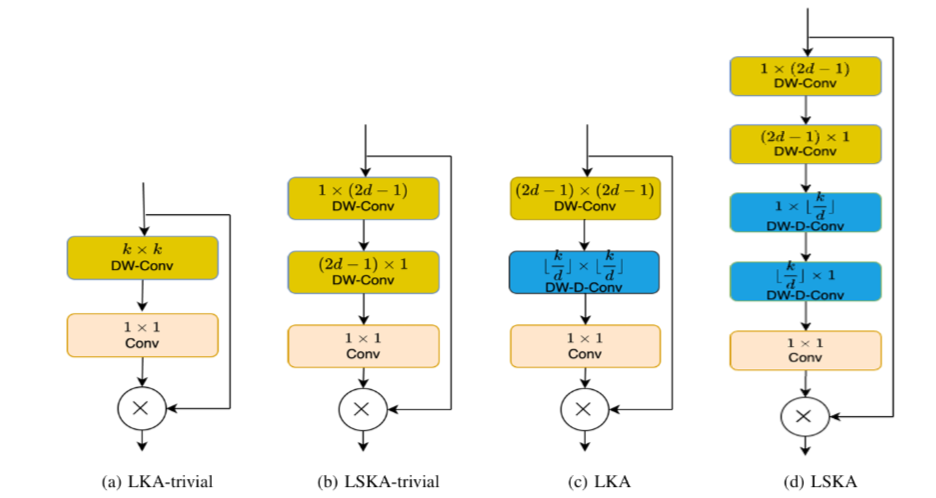
YoloV8改进策略:独家原创,LSKA(大可分离核注意力)改进YoloV8,比Transformer更有效,包括论文翻译和实验结果
文章目录 摘要论文:《LSKA(大可分离核注意力):重新思考CNN大核注意力设计》1、简介2、相关工作3、方法4、实验5、消融研究6、与最先进方法的比较7、ViTs和CNNs的鲁棒性评估基准比较8、结论YoloV8官方结果改进一:测试结果摘要 本文给大家带来一种超大核注意力机制的改进方…...
7天易语言从入门到实战(一)
1.1易语言简介 易语言是一门有着伟大理想的语言。公司用的少,开发者也很少,并不影响国人对他的热情。曾经的多玩LOL,朗读女,都是陪伴再那个国产PC应用匮乏的时代。 2001年1月 吴涛研发了中国自主知识产权的的中文编程语言——易语…...
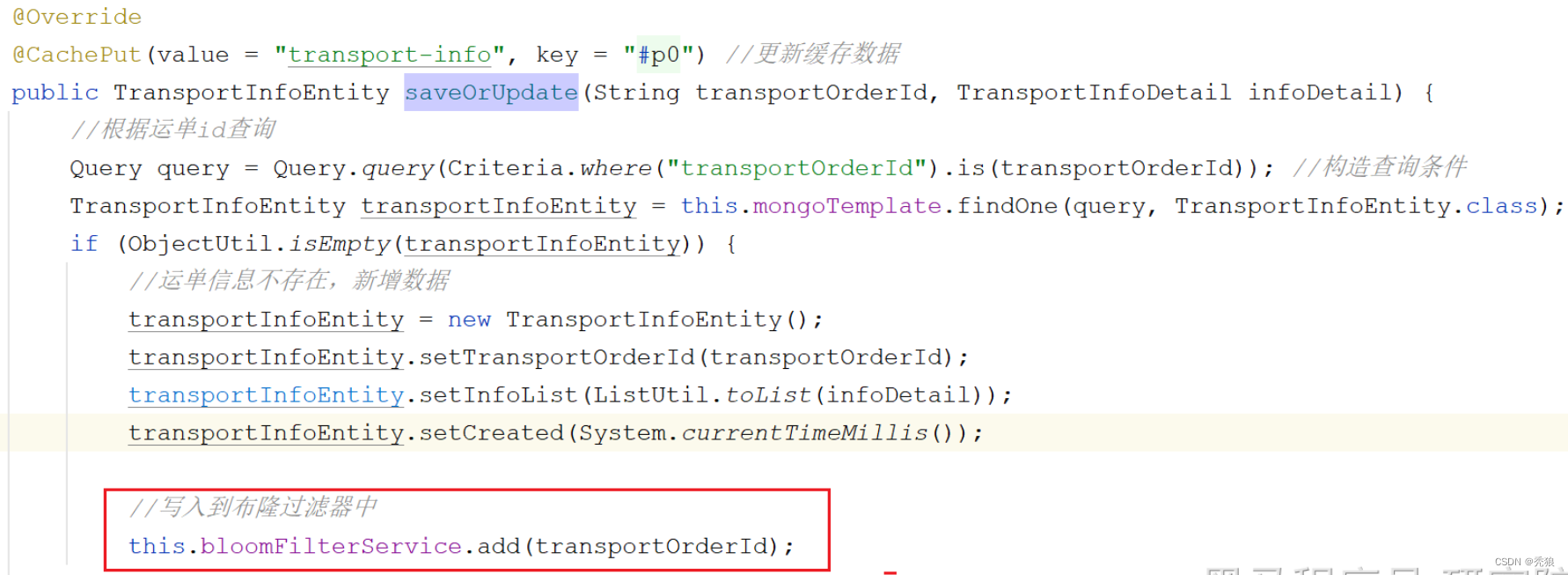
redis缓存问题
缓存击穿 缓存击穿是指某个热点数据存储在redis中,该数据在高并发的场景下,当该key过期时就会有大量的请求去查询数据库,对数据库的压力非常大,可能会导致数据库压垮。 解决方案 1.不为热点的key设置过期时间。 2.使用分布式锁…...

mysql创建自定义函数报错
mysql创建自定义函数报错:This function has none of DETERMINISTIC, NO SQL, or READS SQL DATA in its declarat… 这是我们开启了bin-log,我们就必须指定我们的函数是否是 1.DETERMINISTIC 不确定的 2.NO SQL没有sql语句,当然也不会修改数…...

Docker 的数据管理与网络通信以及Docker镜像的创建
目录 Docker的数据管理 1、数据卷 2、数据卷容器 3、端口映射 4、容器互联 二、Docker网络 1、Docker网络实现原理 2、Docker的网桥模式 1)Host 2)Container 3)none 4)bridge 5)自定义网络 3、创建自定义…...

linux系统查看bash的history
要输出最近的20条命令,可以使用history命令。在Bash终端中,输入以下命令即可获取最近的20条命令历史记录: history 20这将显示你最近执行的20条命令及其相应的行号。 要将最近的20条命令写入到一个名为 “command.txt” 的文本文件中&#…...
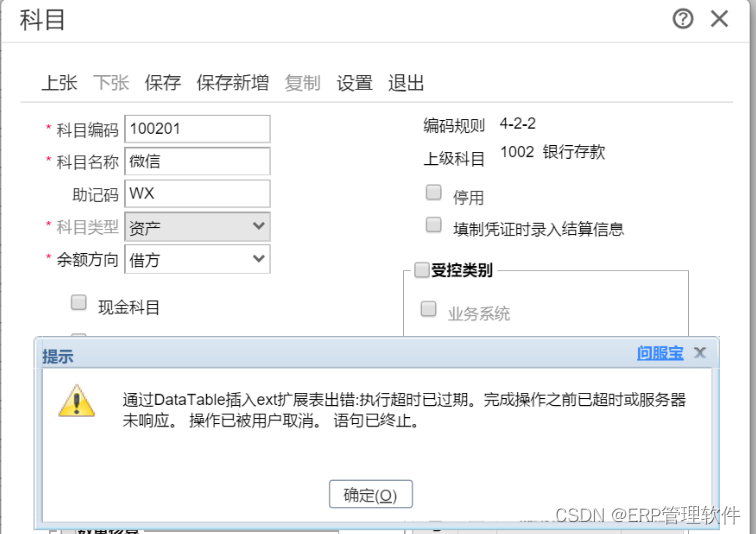
【T+】畅捷通T+增加会计科目提示执行超时已过期。
【问题描述】 在畅捷通T软件中, 增加会计科目的时候提示: 通过DataTable插入ext扩展表出错:执行超时已过期。 完成操作之前已超时或服务器未响应。 操作已被用户取消。 语句已终止。 【解决方法】 【方法一】 注销用户登录,回到软件登录界面…...
0基础学习VR全景平台篇第111篇:全景图拼接和编辑 - PTGui Pro教程
上课!全体起立~ 大家好,欢迎观看蛙色官方系列全景摄影课程! 前情回顾:上节,我们将源图像导入了PTGui,也设置好了各项参数。 下面我们就开始拼接全景图,并且在编辑器里进行一系列检查错位和设…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
