算法23:多叉树_派对的最大快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级.
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大
给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
员工信息的定义如下:
class Employee {public int happy; // 这名员工可以带来的快乐值List<Employee> nexts; // 这名员工有哪些直接下级
}
这道算法题我是花了一整天时间才理清楚的,光靠想象力会把自己给绕晕了。
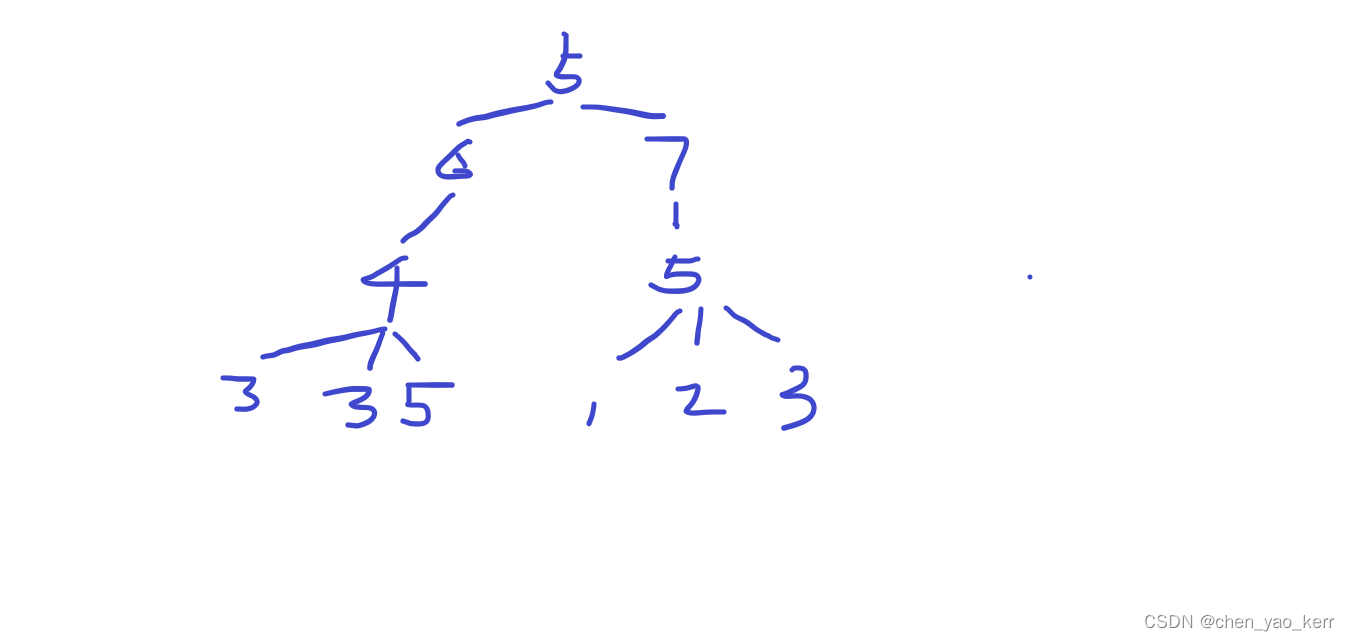
分析:假设2个变量missMax 和 joinMax分别记录当前节点参加、缺失时有可能获得的最大快乐值
1)叶子节点是没有子节点的,因此我们可知,如果叶子节点不能参加,那么返回的信息就该为0,如果可以参加,那么他们的返回信息就该为当前叶子结点本身的快乐值。
2)左子树4下方有3个节点,分别为3、3、5.
a) 如果节点4参加,那么子节点就不能参加,因此,当前节点4的最大快乐值为 4,即 joinMax = 4;missMax =0;
b) 如果4节点不参加,那么4节点及子节点就有可能获得的最大快乐值为 3+3+5 = 11,即 missMax = 11; 当然,他们的子节点也依旧可能全部不参加,即 joinMax =0;
c) 总结:如果4节点参加,获得的最宽快乐值为4,即joinMax = 4, 如果4不参加,获得的最大快乐值为11,即missMax = 11
3)分析6节点
a) 如果6节点参加,那么4节点就不能参加,那么有可能获得的最大值最大值就为 6 + 11 = 17, 即 joinMax = 17. 这个11是我们第2步b步骤推导出来的
b) 如果6节点不参加,那么4节点如果参加,因此,最大值就为4,即missMax=4, 由第2步a步骤推导出来。
c)如果6节点不参加,4节点也不参加,那么4节点的子节点就可以参加了,此时最大快乐值就可得到 3+3+5=11,即missMax = 11
d) 6不参加,4参加,最大快乐值为4,即missMax=4; 6不参加,4不参加,得到的最大快乐值为11,即missMax = 11。最终,我们可以根据步骤b和c得到6不参加,可以获得的最大快乐值为11,missMax = 11。
e) 最终6节点,我们可知:6节点参加,最大快乐值可得到17,即 joinMax = 17;6节点不参加,可得到最大快乐值为11,即missMax = 11
下面分析右子树
1. 节点5
a) 如果5节点参加,最大快乐值为5,即joinMax = 5;
b) 如果5不参加,那么最大快乐值为 1+2+3 =6; 即 missMax =6;
2. 节点7
a) 如果节点7参加,那么5就不可以参加,因此最大快乐值为 7+6=13,即joinMax=13,6是由步骤1的b得到
b)如果7不参加,5也不参加,那么最大快乐值就是6,即missMax=6
c)如果7不参加,5参加, 那么最大快乐值就是5,即missMax=5 (小于6)
d) 总结:7参加,可得最大快乐值joinMax=13, 7不参加,可得最大快乐值为missMax=6
此时,返回到根节点进行分析,根节点值也为5
a)根节点参加,节点6和7都不能参加。可得到 5 + 11 + 6 = 22
b) 根节点不参加,那么6和7就可以参加了,可得 17 + 13 = 30.
全部理解上面的分析以后,我们再来看看下面的绘图:
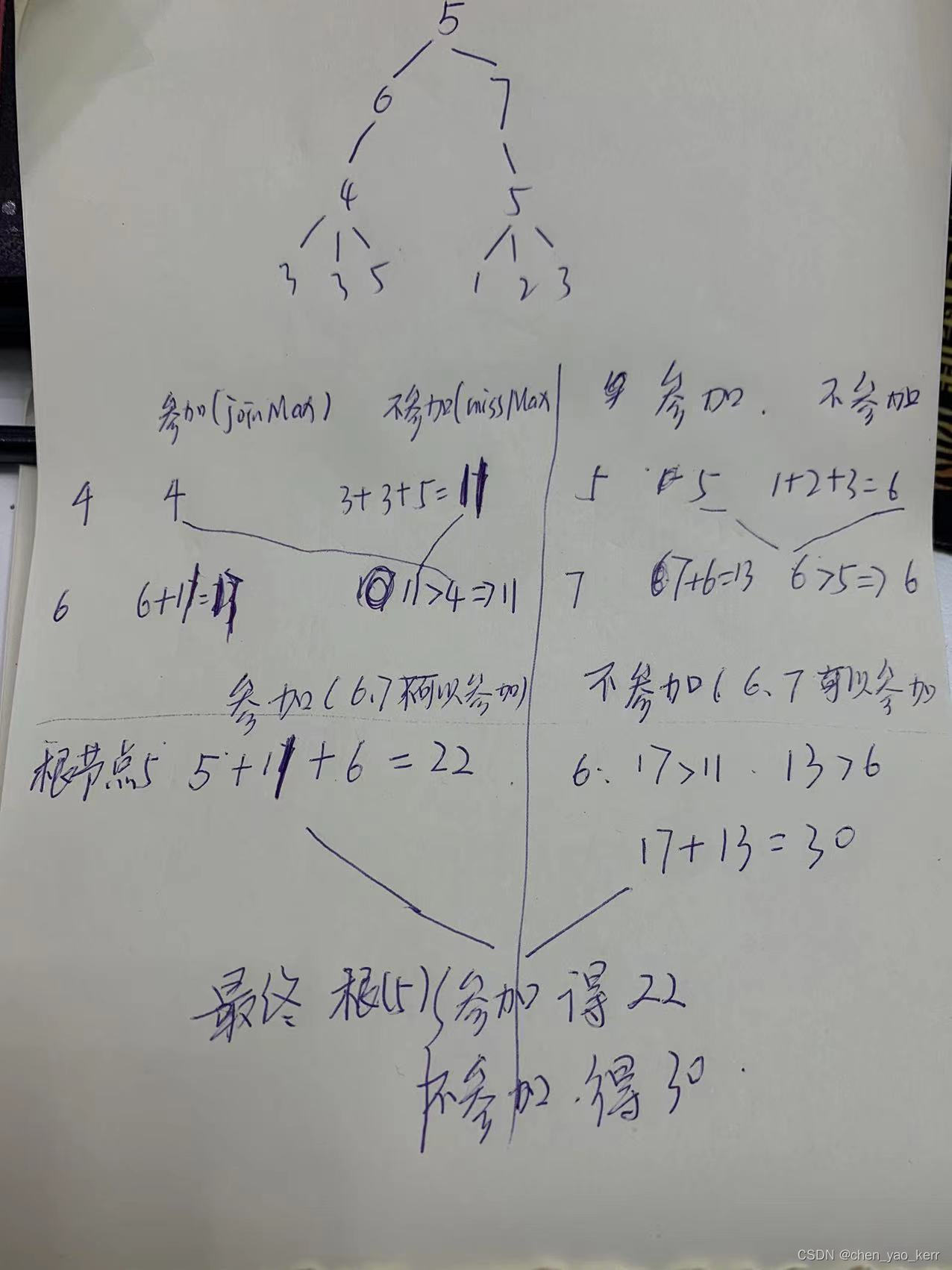
最后,看用套路写代码:
package code03.二叉树_02;import java.util.ArrayList;
import java.util.List;/*** 公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。* 树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。* 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。** 这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:* 1.如果某个员工来了,那么这个员工的所有直接下级都不能来* 2.派对的整体快乐值是所有到场员工快乐值的累加* 3.你的目标是让派对的整体快乐值尽量大* 给定一棵多叉树的头节点boss,请返回派对的最大快乐值。*/
public class Code12_MaxHappyTree {static class Employee {int happy;List<Employee> nexts;Employee (int happy) {this.happy = happy;nexts = new ArrayList<>();}}public static class Info {//当前层参加的值public int joinMax;//当前层缺失时候的值public int missMax;public Info(int join, int miss) {this.joinMax = join;this.missMax = miss;}}public int maxHappy (Employee boss){if (boss == null) {return 0;}int join = process(boss).joinMax;int miss = process(boss).missMax;System.out.println("领导参加, happy值为 :" + join);System.out.println("领导不参加, happy值为 :" + miss);System.out.println("happy的最大值为值为 :" + Math.max(join, miss));return Math.max(join, miss);}public static Info process(Employee cur) {if (cur == null) {return new Info(0, 0);}//记录当前节点参加时的最大快乐值int curJoin = cur.happy;//记录当前节点不参加时的最大快乐值int curMiss = 0;for (Employee e : cur.nexts) {Info info = process(e);//当前层参加,则代表下一层不能参加。因此要获取下一层不能//参加情况下的最大快乐值curMiss += Math.max(info.missMax, info.joinMax);//当前层参加,则获取下一层不参加情况的最大值curJoin += info.missMax;}return new Info(curJoin, curMiss);}public static void main(String[] args) {Employee e31 = new Employee(3);Employee e32 = new Employee(3);Employee e33 = new Employee(5);Employee e3 = new Employee(4);e3.nexts.add(e31);e3.nexts.add(e32);e3.nexts.add(e33);Employee e41 = new Employee(1);Employee e42 = new Employee(2);Employee e43 = new Employee(3);Employee e4 = new Employee(5);e4.nexts.add(e41);e4.nexts.add(e42);e4.nexts.add(e43);Employee e1 = new Employee(6);e1.nexts.add(e3);Employee e2 = new Employee(7);e2.nexts.add(e4);Employee boss = new Employee(5);boss.nexts.add(e1);boss.nexts.add(e2);Code12_MaxHappyTree test = new Code12_MaxHappyTree();int a = test.maxHappy(boss);System.out.println(a);}
}
相关文章:

算法23:多叉树_派对的最大快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每…...

中国ETC行业市场规模及未来发展趋势
中国ETC行业市场规模及未来发展趋势编辑根据市场调研在线网发布的2023-2029年中国ETC行业发展策略分析及战略咨询研究报告分析:随着政府坚持实施绿色出行政策,ETC行业也受到了极大的支持。根据中国智能交通协会统计,2017年中国ETC行业市场规模…...
——只出现一次的数字)
每日刷题(一)——只出现一次的数字
前言 今天遇到一个位运算的题目,感觉很有意思,记录一下。 Question1 136. 只出现一次的数字 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实…...
洛谷P5737 【深基7.例3】闰年展示 C语言/C++
【深基7.例3】闰年展示 题目描述 输入 x,yx,yx,y,输出 [x,y][x,y][x,y] 区间中闰年个数,并在下一行输出所有闰年年份数字,使用空格隔开。 输入格式 输入两个正整数 x,yx,yx,y,以空格隔开。 输出格式 第一行输出一个正整数&a…...

shell注释
注释对于任何编程语言都是不可忽视的重要组成部分,编写者通过注释来为其他人提供解释或提示,能有效提高代码的可读性。 Bash 同其他编程语言一样提供了两种类型注释的支持。 单行注释多行注释一、Bash 单行注释 在注释段落的开头使用 # ,如下…...
【C++入门(上篇)】C++入门学习
前言: 在之前的学习中,我们已经对初阶数据结构进行相应了学习,加上之前C语言的学习功底。今天,我们将会踏上更高一级“台阶”的学习-----即C的学习!!! 文章目录1.C 简介1.1什么是C1.2.C的发展史…...

【密码学】 一篇文章讲透数字签名
【密码学】 一篇文章讲透数字签名 数字签名介绍 数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名…...

POI导入导出、EasyExcel批量导入和分页导出
文件导入导出POI、EasyExcel POI:消耗内存非常大,在线上发生过堆内存溢出OOM;在导出大数据量的记录的时候也会造成堆溢出甚至宕机,如果导入导出数据量小的话还是考虑的,下面简单介绍POI怎么使用 POI导入 首先拿到文…...

手把手教你做微信公众号
手把手教你做微信公众号 微信公众号可以通过注册的方式来建立。 1.进入微信公众平台 首先,在浏览器中搜索微信公众号,网页第一个就是,如下图所示,我们点进去。 2.注册微信平台账号 进入官网之后,如下图所示&#…...
python-在macOS上安装python库 xlwings失败的解决方式
问题:python库 xlwings安装失败 今天,看到网上有wlwings库,可以用来处理excel表格,立刻想试一试。结果,安装这个python库失败了。经过排查,问题解决。 安装过程和错误提示: 我用最简单直接的…...
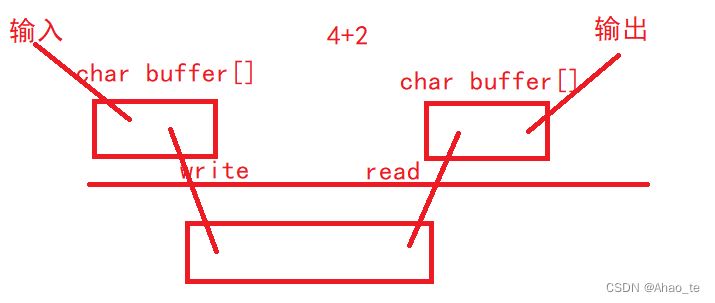
【Linux】进程间通信(匿名管道和命名管道通信、共享内存通信)
文章目录1、进程间通信1.1 进程的通信1.2 如何让进程间通信?1.3 进程间通信的本质2、管道通信2.1 匿名管道2.2 匿名管道通信2.3 命名管道2.4 命名管道的通信3、SystemV中的共享内存通信3.1 共享内存3.2 共享内存的通信3.3 共享内存的缺点以及数据保护3.4 共享内存的…...

漏洞分析: WSO2 API Manager 任意文件上传、远程代码执行漏洞
漏洞描述 某些WSO2产品允许不受限制地上传文件,从而执行远程代码。以WSO2 API Manager 为例,它是一个完全开源的 API 管理平台。它支持API设计,API发布,生命周期管理,应用程序开发,API安全性,速…...

详解Android 13种 Drawable的使用方法
前言关于自定义View,相信大家都已经很熟悉了。今天,我想分享一下关于自定义View中的一部分,就是自定义Drawable。Drawable 是可绘制对象的一个抽象类,相对比View来说,它更加的纯粹,只用来处理绘制的相关工作…...

MakeFile教程
前言 当我们需要编译一个比较大的项目时,编译命令会变得越来越复杂,需要编译的文件越来越多。其 次就是项目中并不是每一次编译都需要把所有文件都重新编译,比如没有被修改过的文件则不需要重 新编译。工程管理器就帮助我们来优化这两个问题…...
Spring使用mongoDB步骤
1. 在Linux系统使用docker安装mongoDB 1.1. 安装 在docker运行的情况下,执行下述命令。 docker run \ -itd \ --name mongoDB \ -v mongoDB_db:/data/db \ -p 27017:27017 \ mongo:4.4 \ --auth执行docker ps后,出现下列行,即表示mongoDB安…...
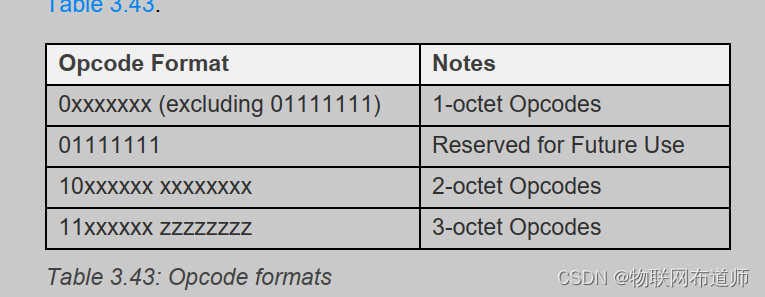
【蓝牙mesh】access层(接入层)协议介绍
【蓝牙mesh】access层(接入层)协议介绍 Access层简介 Access层定义了应用层如何使用upper协议层的接口,它不仅定义了应用层的格式,还定义了应用数据在upper层的加密和解密。当收到下层的数据包时,它会检查数据的netke…...

【一天一门编程语言】JavaScript 语言程序设计极简教程
JavaScript 语言程序设计极简教程 用 markdown 格式输出答案。 不少于3000字。细分到2级目录。 一、JavaScript 简介 1.1 什么是 JavaScript JavaScript 是一种由Netscape的LiveScript发展而来的脚本语言,是一种动态类型、弱类型、基于原型的语言,内…...

CMake调试器出炉:调试你的CMake脚本
Visual Studio 开发团队一直和 Kitware 紧密合作,致力于开发一个用于调试 CMake 脚本的调试器。 我们将继续这个工作,以便开发人员社区可以通过添加新功能和对其他 DAP 功能的支持来共同改进它。 我们很高兴地宣布,CMake 调试器的预览版现在…...
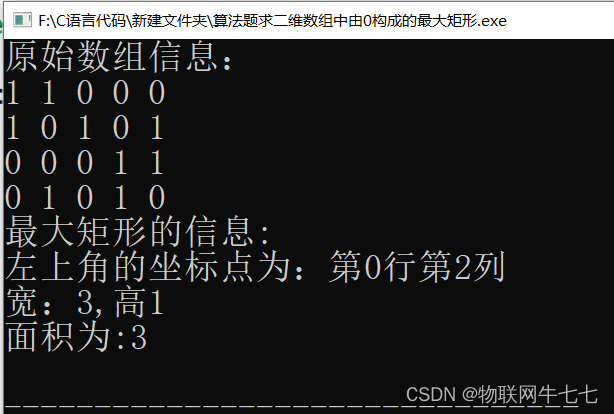
题解 # 二维矩阵最大矩形问题#
题目: 小明有一张N*M的方格纸,且部分小方格中涂了颜色,部分小方格还是空白。 给出N (2<Ns30)和M(2sMs30)的值,及每个小方格的状态((被涂了颜色小方格用数字1表示,空白小方格用数字0表示); 请…...
奔四的路上,依旧倔强的相信未来
本文首发于2022年12月31日 原标题: 奔四的路上,依旧倔强的相信未来!–我的2022年终总结 读大学那几年,一直保持着写日记和做计划的习惯,还记得大学毕业刚开始打工的时候,我的床头的墙上一定会画一张表,写上一个月的计划和一周的计划 计划也会有完不成的时候,但加深了…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
