基于粒子群算法的无人机航迹规划-附代码
基于粒子群算法的无人机航迹规划
文章目录
- 基于粒子群算法的无人机航迹规划
- 1.粒子群搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用粒子群算法来优化无人机航迹规划。
1.粒子群搜索算法
粒子群算法原理请参考:网络博客
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得粒子群搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用粒子群算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,粒子群算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于粒子群算法的无人机航迹规划-附代码
基于粒子群算法的无人机航迹规划 文章目录 基于粒子群算法的无人机航迹规划1.粒子群搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用粒子群算法来优化无人机航迹规划。 1.粒子群…...
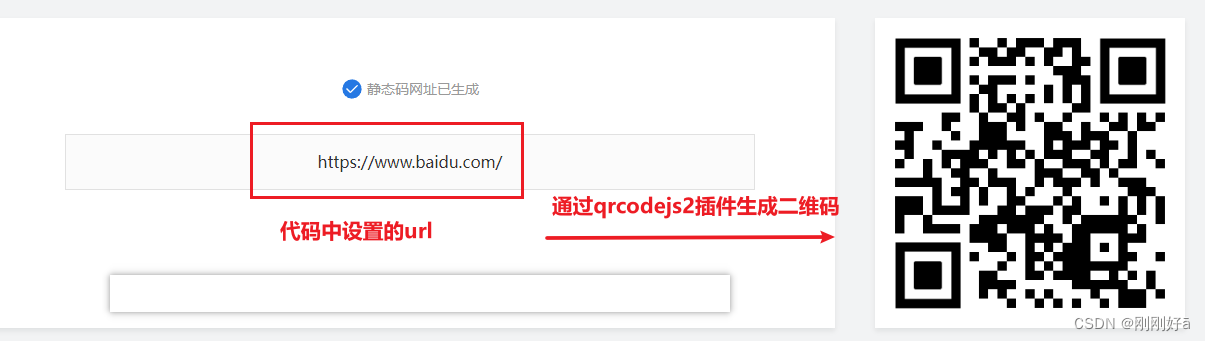
前端使用qrcodejs2插件实现根据网址生成二维码
实现效果: 实现方法: 1.安装插件 npm install --save qrcodejs2 2.可以全局引入,也可以只在使用的vue文件中引入 import QRCode from qrcodejs2; 3.在vue文件的template中设置放置二维码的div <div id"qrcode"></di…...
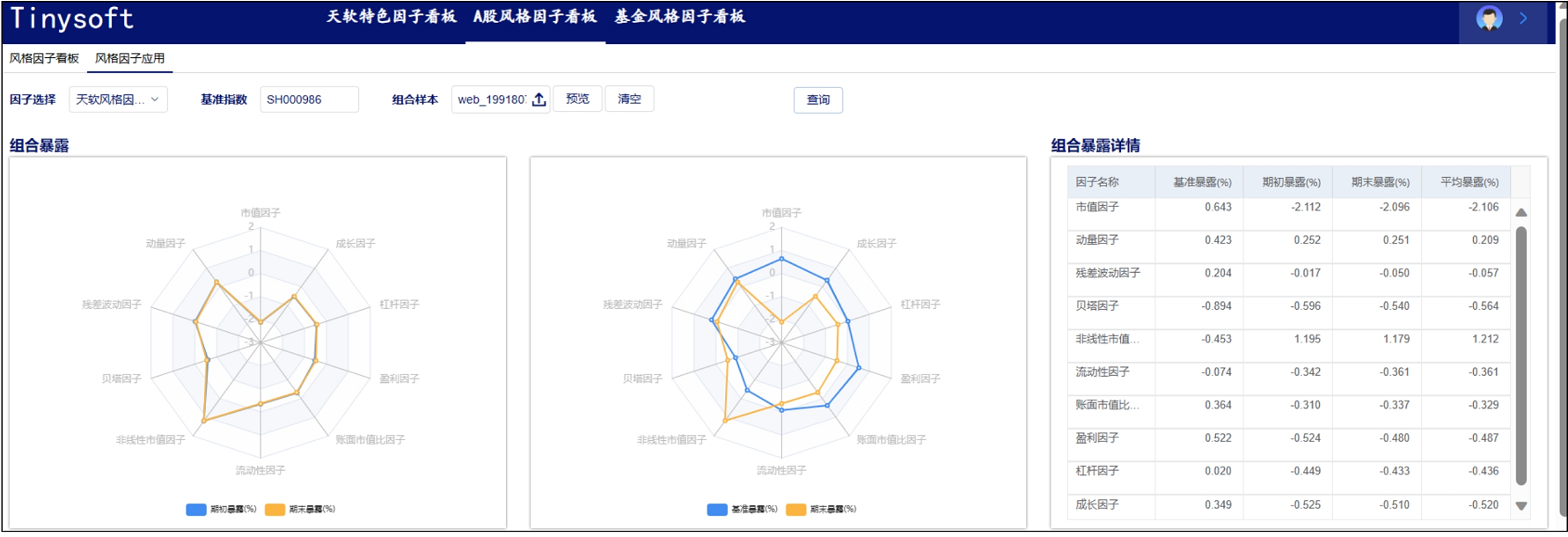
A股风格因子看板 (2023.10 第11期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第11期,指数组合数据截止日2023-09-30,要点如下 近1年A股风格因子检验统…...

anaconda安装python 3.11
最近需要测试gpt researcher项目,gpt researcher项目的环境是3.11,于是用anaconda创建一个虚拟环境,结果报错了: UnsatisfiableError: The following specifications were found to be incompatible with each other:Package xz c…...

问题:EventSource 收不到流数据及 EventSource 的 onmessage 方法为null
文章目录 问题分析问题 在开发时,有用到 EventSource,但是在 new EventSource 的时候,打印 new EventSource 如下: onmessage : null, onerror : null, onopen: f(event)前端...

P2 B+树索引
文章目录 Task1 B树页B树页B树内部结点B树叶子结点 Task2 B树操作Task2 B树插入和搜索的单一值插入单一值搜索单一值 Task2 B树删除 Task3 叶子扫描的迭代器Task4 并行索引 Task1 B树页 B树页 实际上是每个B树页面的标题部分,包含叶子页面和内部页面共享的信息。 …...

爬虫知识之BeautifulSoup库安装及简单介绍
一. 前言 在前面的几篇文章中我介绍了如何通过Python分析源代码来爬取博客、维基百科InfoBox和图片,其文章链接如下: 其中核心代码如下: # coding=utf-8 import urllib import re #下载静态HTML网页 url=http://www.csdn.net/ content = urllib.urlopen(url).read…...

如何有效取代FTP来帮助企业快速传输大文件
在互联网的发展历史上,FTP是一种具有里程碑意义的协议,它最早出现在1971年,是实现网络上文件传输的基础。FTP的优点是简单、稳定、兼容性强,可以在不同的操作系统和平台之间进行文件交换。然而,时代在进步,…...

免登陆积分商城原理
有客户需要免登陆积分商城,研究了一下发现免登陆用途广泛,实现原理也很简单。如果是浏览器无非就是使用fingerprintjs2之类的扩展来实现获取浏览器指纹ID,如果是APP就获取设备唯一标识,然后在使用cryptojs加密来传递到php…...

muduo源码学习base——Atomic(原子操作与原子整数)
Atomic(原子操作与原子整数) 前置知识AtomicIntegerTget()getAndAdd()getAndSet() 关于原子操作实现无锁队列(lock-free-queue) 前置知识 happens-before: 用来描述两个操作的内存可见性 如果操作 X happens-before 操作 Y,那么 X 的结果对于…...
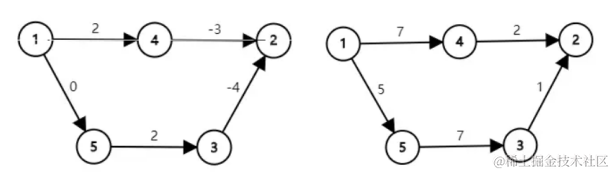
最短路相关笔记
Floyd Floyd 算法,是一种在图中求任意两点间最短路径的算法。 Floyd 算法适用于求解无负边权回路的图。 时间复杂度为 O ( n 3 ) O(n^3) O(n3),空间复杂度 O ( n 2 ) O(n^2) O(n2)。 对于两点 ( i , j ) (i,j) (i,j) 之间的最短路径,有…...

Web前端-Vue2+Vue3基础入门到实战项目-Day5(自定义指令, 插槽, 案例商品列表, 路由入门)
自定义指令 基本使用 自定义指令: 自己定义的指令, 可以封装一些dom操作, 扩展额外功能全局注册// 1. 全局注册指令 Vue.directive(focus, {// inserted 会在 指令所在的元素, 被插入到页面中时触发inserted (el) {// el 就是指令所绑定的元素// console.log(el)el.focus()} …...

mysql json数据类型 相关函数
创建JSON文本的函数 1.JSON_ARRAY(转换json数组) 2.JSON_OBJECT(转换json对象) 3.JSON_QUOTE(转义字符串) 搜索JSON文本的函数 1.JSON_CONTAINS(json当中是否包含指定value) 2.J…...

如何实现前端实时通信(WebSocket、Socket.io等)?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

使用 SSSD 进行网络用户身份验证
文章目录 使用 SSSD 进行网络用户身份验证SSSD和Active Directory先决条件、假设和要求软件安装加域 SSSD配置自动创建HOME目录 检查和验证 Kerberos票证已知的问题参考 使用 SSSD 进行网络用户身份验证 SSSD 代表系统安全服务守护程序,它实际上是处理来自各种网络…...

紫光展锐携中国联通完成RedCap芯片V517孵化测试
近日,紫光展锐携手中国联通5G物联网OPENLAB开放实验室(简称“OPENLAB实验室”)共同完成RedCap芯片V517创新孵化,并实现在联通5G全频段3.5GHz、2.1GHz、900MHz下的端到端业务验证测试。 V517是一款基于紫光展锐5G成熟平台设计与研发…...

算法通关村第十一关青铜挑战——移位运算详解
大家好,我是怒码少年小码。 计算机到底是怎么处理数字的? 数字在计算机中的表示 机器数 一个数在计算机中的二进制表示形式,叫做这个数的机器数。 机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0&am…...

2023年面试测试工程师一般问什么问题?
面试和项目一起,是自学路上的两大拦路虎。面试测试工程师一般会被问什么问题,总结下来一般是下面这4类: 1.做好自我介绍 2.项目相关问题 3.技术相关问题 4.人事相关问题 接下来,主要从以上四个方向分别展开介绍。为了让大家更有获…...
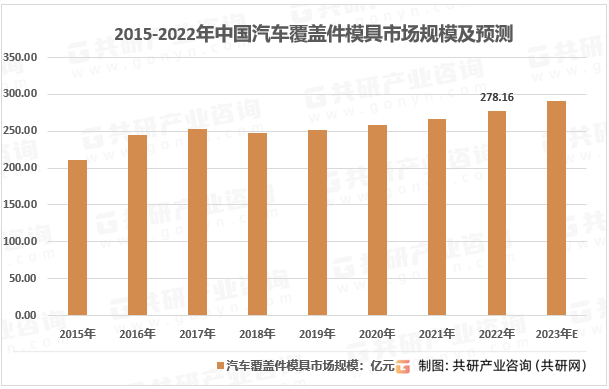
2023年中国汽车覆盖件模具竞争格局、市场规模及行业需求前景[图]
汽车覆盖件模具是汽车车身生产的重要工艺装备,其设计和制造时间约占汽车开发周期的 2/3,是汽车换型的重要制约因素之一。汽车覆盖件模具具有尺寸大、工作型面复杂、技术标准高等特点,属于技术密集型产品。汽车覆盖件模具按以其冲压的汽车覆盖…...
vue3项目运行报错import zhCn from “element-plus/lib/locale/lang/zh-cn“
解决办法 import zhCn from "element-plus/lib/locale/lang/zh-cn";修改为 import zhCn from "element-plus/dist/locale/zh-cn.mjs";...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
