计算机考研自命题(5)
1、C语言–求和
1、展开式求和。输入一个实数x,计算并输出下式的和,直到最后一项的绝对值小于0.00001.计算结果保留2位小数,试编程。
S = x + x²/2!+ x³/3!+ …
/*
算法思想:定义一个求阶乘的函数fact(),
头文件调用math.h函数库:pow()函数求次幂,fabs()函数取绝对值
直到最后一项的绝对值小于0.00001,则输出求和结果,结果保留两位小数
*/
#include<stdio.h>
#include<math.h>// 求阶乘
int fact(int n){int i,sum=1;for(i=1;i<=n;i++){sum=sum*i;}return sum;
}int main(){int a,n,i;double x,result,s=0;scanf("%lf",&x);for(i=1;(pow(fabs(x),i)/fact(i))>=0.00001;i++){result=pow(x,i)/fact(i);s+=result;}printf("s=%.2lf",s);return 0;
}
2、C语言–元素移动
2、有n个整数,使前面各数顺序向后移动m个位置,移出的数再从头移入,编得一个函数实现以上功能,在主函数中输入n个整数
并输出调整后的n个数。
# include<stdio.h>/*
解题思路:
定义一个数组t存放传入的数组A,然后跟据移动的情况从t中取出元素从新放回A中
remove(*A,5,3)假设有5个元素,向后移动3位
A={1,2,3,4,5} ==> A={3,4,5,1,2}
首先就是将t中下标为 5-3 = 2 的元素一次存放到A中,
然后将剩余的元素放入A中
*/// 元素移动的方法
void remove(int *A,int n,int m) { // n表示元素个数,m表示移动几位int t[100]; // 用于存储A[]中的元素 int i;for(i=0; i<n; i++) { // 将A中的元素全部存储到t中 t[i] = A[i];}for(i = 0 ; i<m; i++) { // 将t 中 下标>=n-m的元素存放到A中 A[i] = t[n-m+i];}for(i = m; i<n; i++) { // 将剩余的元素存放到A中 A[i] = t[i-m];}for(i = 0; i<n; i++) { // 遍历 printf("%d ",A[i]);}
}int main() {int i,x,num;scanf("%d",&num);int A[num];for(i = 0; i<num; i++) {printf("请输入第%d个元素",i+1);scanf("%d",&x);A[i] = x;}printf("移动后的元素序列");remove(A,num,3);return 0;
}
3、C语言-文件操作
3、将C盘根目录下文件from.txt的内容复制到to.txt文件中,to.txt与from.txt在同一目录。
/*
解题思路:首先以只读的方式打开文件from.txt,然后以写的方式打开文件to.txt,
使用fgetc()函数将文件from.txt里面的字符一个一个读取出来,然后用fputc()函数将读取出的文件写入to.txt中
*/# include <stdio.h>
int main()
{// 文件复制FILE *fp1,*fp2;char ch;// 打开文件 fp1 = fopen("from.txt","r");if(fp1 == NULL){printf("文件打开失败!\n"); } fp2 = fopen("to.txt","w");if(fp2 == NULL){printf("文件打开失败:\n"); }// 将读取出来的文件写入 to.txt 中 while((ch = fgetc(fp1)) != EOF){fputc(ch,fp2);}// 文件关闭 fclose(fp1);fclose(fp2); return 0; }
4、C语言–复数计算
4、要求设计函数完成两个复数相乘的算法。在主函数中输入两个复数,计算后输出乘积结果
/*
解题思路:
复数的运算 i*i = -1
(a+bi)* (c+di) = a*c + a*di- b*d +b*ci
*/
//复数的结构体定义如下:
struct Complex{float real;float imag;
}Complex;
//要求设计函数完成两个复数相乘的算法。在主函数中输入两个复数,计算后输出乘积结果。Complex Mul(Complex c1,Complex c2){Complex product;product.real = c1.real*c2.real - c1.imag*c2.imag; // 乘积以后的虚部 i*i = -1product.imag = c1.imag*c2.real + c1.real*c2.iamg; // 虚部return product;
}
5、数据结构
5、下面程序段的功能是建立二叉树的算法,请在下划线处填上正确的内容。
typedef struct node{
int data;
struct node *lchild;
____struct node *rchild____;
}bitree;
void createbitree(bitree *&bt) {
scanf( “%c”,&ch);
if(ch=='#')
____bt->data = ch_______;
else {
bt=(bitree*)malloc(sizeof(bitree));
bt->data=ch;
___createbitree(bt->lchild)_____;
createbitree(bt->rchild);
}
}
6、数据结构
6、建立链表
typedef struct node {
int data;
struct node *next;
} lklist;
void lklistcreate(_____lklist___ *&head ) {
for (i=1;i<=n;i++) {
p=(lklist *)malloc(sizeof(lklist));
scanf( “%d”,&(p ->data));
p->next=0;if(i==1)
head=q=p;
else {
q->next=p;
______q = p______;
}
}
}7、数据结构–链表合并
7、实现链式结构上合并排序的算法
# include<stdio.h>//单链表的定义
typedef struct LNode {ELemType data;LNode *next;
} LNode,*LinkList;/*
将两个递增有序的链表A,B合并成一个递增有序的链表C解题思路:假设A,B带有头指针,定义pa,pb指针分别指向A,B的下一个结点,
运用尾插法,先将A,B中较小的元素插入C中,实现整体按元素值递增有序;
因为A,B链表中的结点个数不一样,
所以当A中的结点数更少时 ,将B中的元素依次加入C中
反之,则将A中的元素依次加入C中
*/
void Merge(LNode A,LNode B,LNode &C) {LNode *pa = A->next;LNode *pb = B->next; LNode *pc = C;while(pa&&pb) { if(pa->data <= pb->data) { // 运用尾插法将小的元素率先加入C链表中pc->next = pa;pc = pa;pa = pa->next;} else {pc->next = pb;pc = pb;pb = pb->next;}}while(pa) {pc->next = pa;pc = pa;pa = pa->next;}while(pb) {pc->next = pb;pc = pb;pb = pb->next;}
}
8、数据结构–二叉树查找
8、实现在二叉树中查找结点x的算法
# include<stdio.h>/*
解题思路:跟据二叉树的先序遍历进行改造,传入该二叉树和要查找的值
先比较根节点是不是寻找的目标结点,如果是就返回结点,不是就寻找递归寻找左子树和右子树
直到二叉树全部查找完
*/// 二叉树的结构定义
typedef struct BiNode{ELemType data;struct BiNode *lchild;struct BiNode *rchild;
}BiNode,*BiTree; BiNode *find_x(BiTree Bt,ELemType x){while(Bt){if(Bt->data == x){return Bt;}*find_x(Bt->lchild,x);*find_x(Bt->lchild,x);}
}
9、数据结构–堆排序
9、关键字序列(k1,k2,k3,…,kn-1)是堆,写出将(k1,k2,k3,…,kn-1,x)调整为堆的算法
# include<stdio.h>
/*
解题思路:堆排序的思路
以大根堆为例:把关键字看成一颗完全二叉树,根节点(堆顶元素)就是整个序列的最大值,输出堆顶元素
堆结构被破坏,然后进行调整,将最大的元素交换到堆顶
从n/2开始依次交换
*/
void adjustHeap(ELemType A[],int len,int k) {int i;A[0] = A[k];// A[0] 暂存子树的根节点for(i = 2*k; i<=len; i*=2) { // 沿K较大的子结点向下筛选if(i<len && A[i]<A[i+1]){i++; // 取K较大的子节点下标 }if(A[0]>=A[i]){ // 筛选结束 break;}else{A[k] = A[i]; // 将A[i] 调整到双亲结点上 k = i; // 修改 k 值,以便继续向下筛选 } }A[k] = A[0]; // 筛选结点放入最终位置
}
10、数据结构–最小生成树
10、给一组数,画邻接矩阵和邻接表,写出prim和克鲁斯卡尔的最小生成树
相关文章:

计算机考研自命题(5)
1、C语言–求和 1、展开式求和。输入一个实数x,计算并输出下式的和,直到最后一项的绝对值小于0.00001.计算结果保留2位小数,试编程。 S x x/2! x/3! … /* 算法思想:定义一个求阶乘的函数fact(), 头文件调…...

【原创】c语言4种字符串函数的代码测试
c语言4种字符串函数的代码测试 1.字符串拼接strcat [contact] 2.字符串复制strcpy 3.带参数的字符串复制strncpy 4.字符串比较strcmp:比第一个不同字母的ascii码,如acb>abc #include<stdio.h> #include<string.h>int main() {char s1[]&…...

扩散模型学习——代码学习
文章目录 引言正文UNet网络结构训练方法DDPM采样方法讲解Context上下文信息添加DDIM的方法详解 总结参考 引言 这是第一次接触扩散模型,为了学习,这里好好分析一下他的代码 正文 UNet网络结构 这部分主要是定义一下网络结构,以及相关的网…...
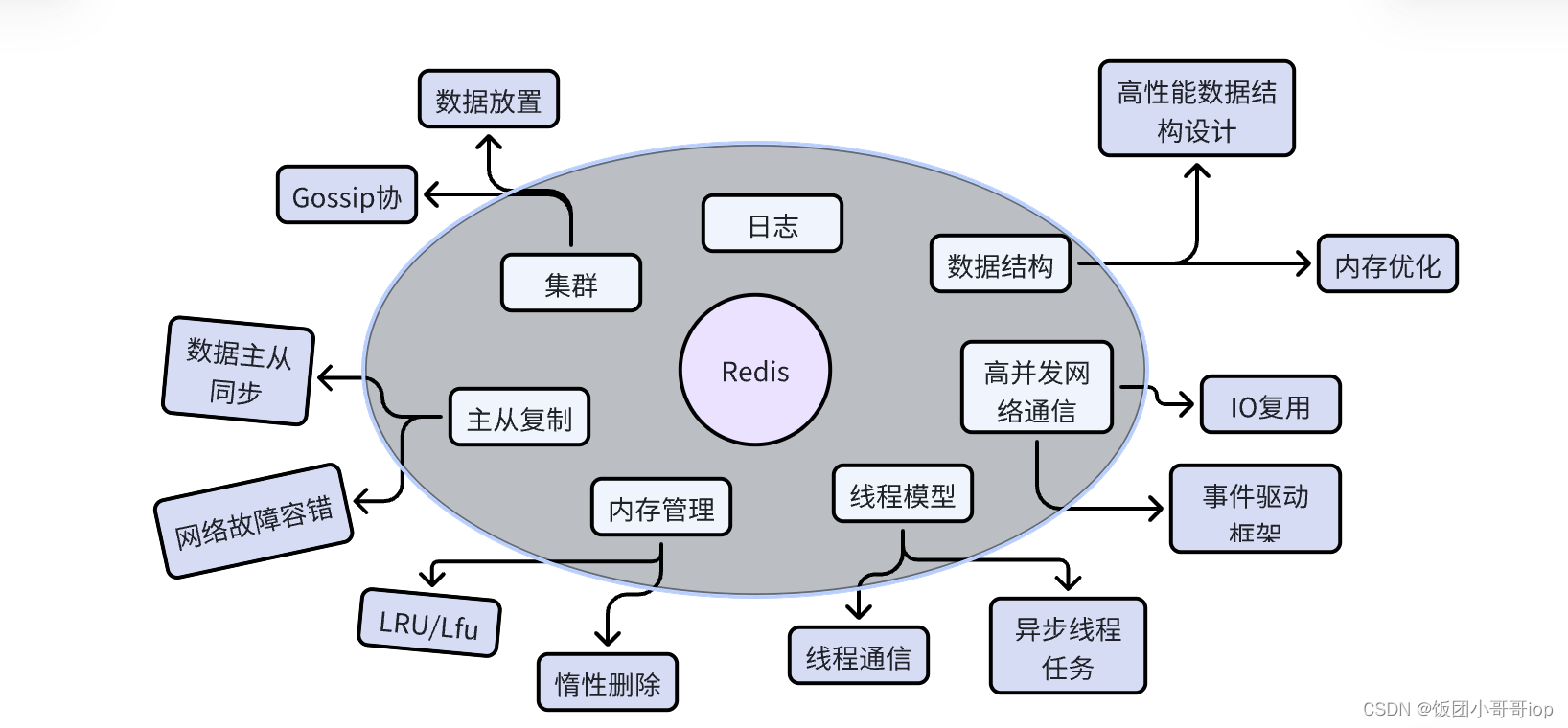
redis 数据结构
一、为什么要扒一下底层技术 首先我是一个解决方案工程师,为什么要看redis底层的设计呢?总结下来分几点: 1. 让系统跑起来更放心 2. 面试中可以对跟对面的牛马侃大山、吹🐮 3. 虚一点,举一反三,学习一下…...

node.js中express框架cookie-parser包设置cookie的问题
后端使用node.js express cookie-parser技术栈设置cookie的时候出现了无法成功设置的问题 前端发送axios请求部分代码: axios({method: "post",data: {content: remark,relatedArticles: relatedArticleId,userId: userId,userEmail: userEmail,topRema…...
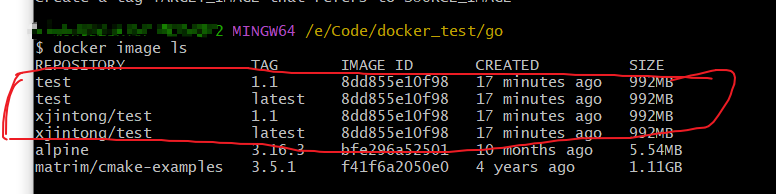
Docker命令手册
大家好,我叫徐锦桐,个人博客地址为www.xujintong.com。平时记录一下学习计算机过程中获取的知识,还有日常折腾的经验,欢迎大家访问。 记录平时用的比较多的Docker命令。 docker学习地址 1、docker停止并删除运行的容器 首先查看…...
Selenium+Pytest自动化测试框架详解
前言 selenium自动化 pytest测试框架 本章你需要 一定的python基础——至少明白类与对象,封装继承;一定的selenium基础——本篇不讲selenium,不会的可以自己去看selenium中文翻译网 一、测试框架简介 测试框架有什么优点 代码复用率高&…...

CentOS7安装部署CDH6.2.1
文章目录 CentOS7安装部署CDH6.2.1一、前言1.简介2.架构3.环境 二、环境准备1.部署服务器2.安装包准备3.修改机器名4.关闭防火墙5.关闭 SELinux6.Hosts文件7.limits文件8.设置swap空间9.关闭透明巨页内存10.免密登录 三、安装CM管理端1.安装第三方依赖包2.安装Oracle的JDK3.安装…...
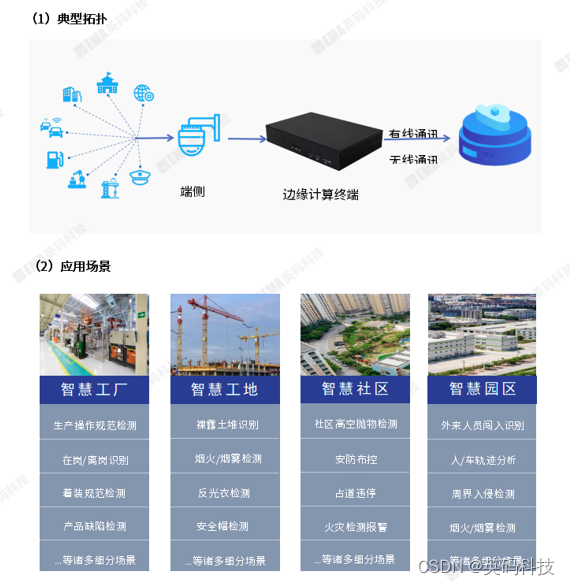
海思Hi3519DV500边缘计算盒子-英码IVP09A,双核A55 64位处理器
产品简介 IVP09A是英码科技推出的边缘计算智能工作站,搭载双核 Cortex-A55 架构AI 处理器;内置高效的神经网络推理引擎,提供2.5TopsNPU算力;支持多路视频图像识别硬件加速。IVP09A,高效能低成本、稳定易开发、多点布线、联网管控…...

理解数据库
文章目录 一、了解什么是信息1.1 信息和数据1.1.1 信息 (information)1.1.2 数据 (Data) 1.2 数据处理 二、如何描述数据具备的信息2.1 数据库的一些术语: 三、数据模型3.1 概念模型 E-R,是对信息世界的建模…...
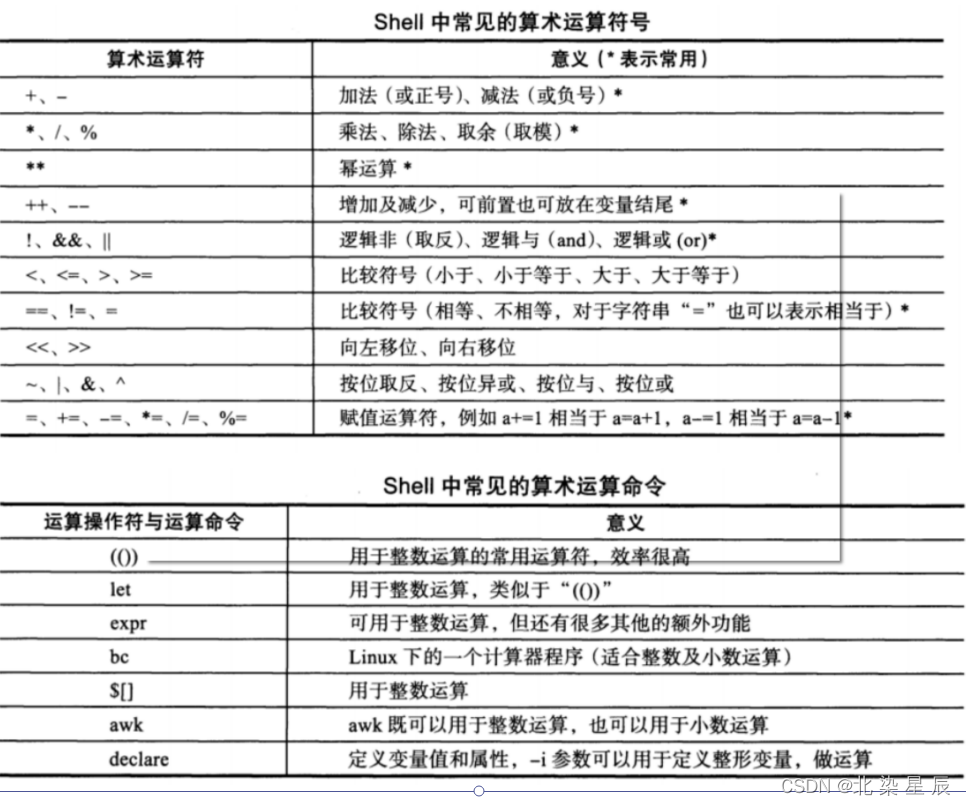
RHCE---Shell基础 2
文章目录 目录 文章目录 前言 一.变量 概述 定义 自定义变量 环境变量 概述: 定义环境变量: 位置变量 "$*"会把所有位置参数当成一个整体(或者说当成一个单词 变量的赋值和作用域 read 命令 变量和引号 变量的作用域 变…...

Git报错解决
本篇主要汇总在使用 Git 进行提交和拉取文件时,遇到的问题的解决方案,以便下次查找。 1 关于使用Git出现“git Failed to connect to 127.0.0.1 port xxxx: Connection refused”的问题解决方案 1. 问题描述 在使用 git 拉取、提交代码的时候ÿ…...
TechSmith Camtasia 2023 for Mac 屏幕录像视频录制编辑软件
TechSmith Camtasia for Mac 2023中文破解版 是一款专业的屏幕录像视频录制编辑软件,非常容易就可以获得精彩的截屏视频。创建引人注目的培训,演示和演示视频。Camtasia 屏幕录制软件简化,直观,让您看起来像专业人士。利用Camt…...
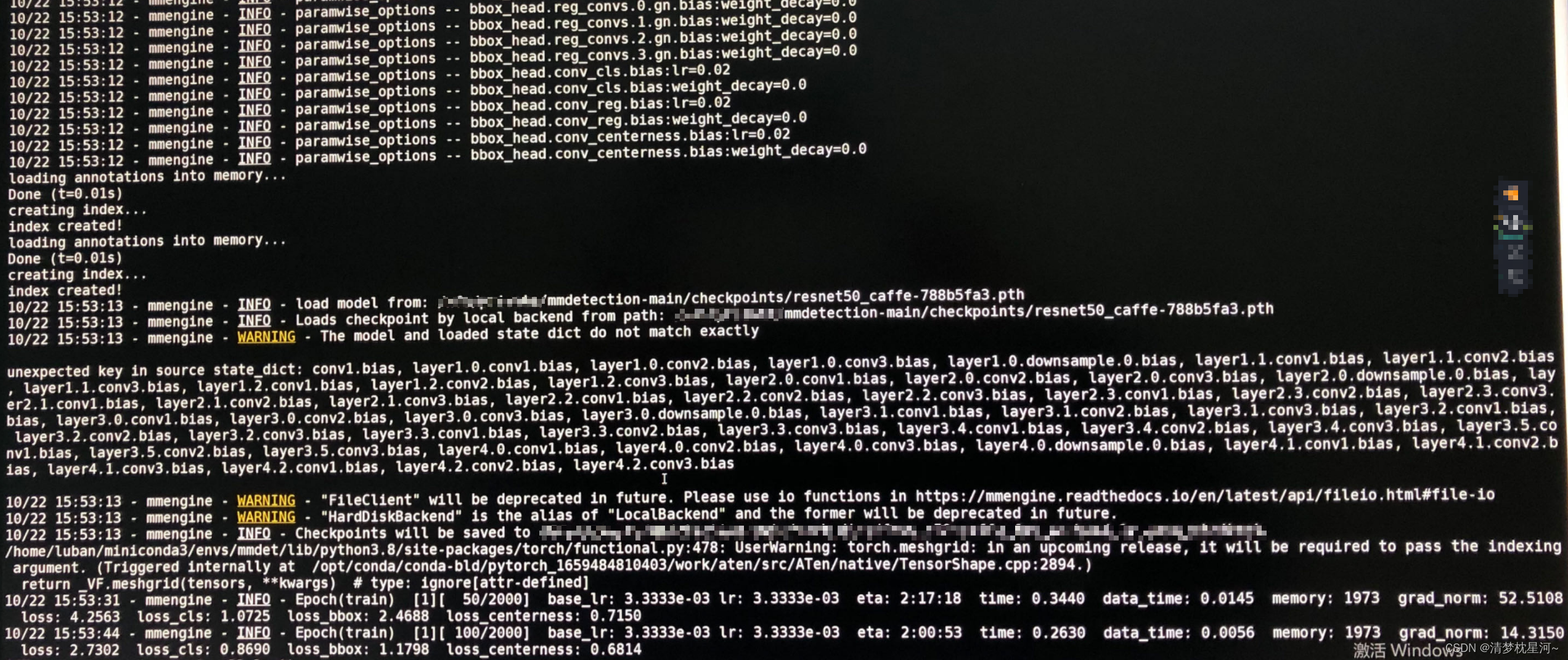
高效MMdetection(3.1.0)环境安装和训练自己数据集教程(实现于Linux(ubuntu),可在windows尝试)
一、前言 很久没用mmdetection了,作为目标检测常见的几个深度学习框架,mmdetection用的人还是很多的,其中比较吸引人的一点就是mmdetection集成了非常多的算法,对于想做实验对比和算法学习的人来说,基于这个框架可以事…...

软考-入侵检测技术原理与应用
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 by 2023年10月 入侵检测技术概念 入侵检测技术是指一种计算机安全技术,旨在监测计算机系统、…...
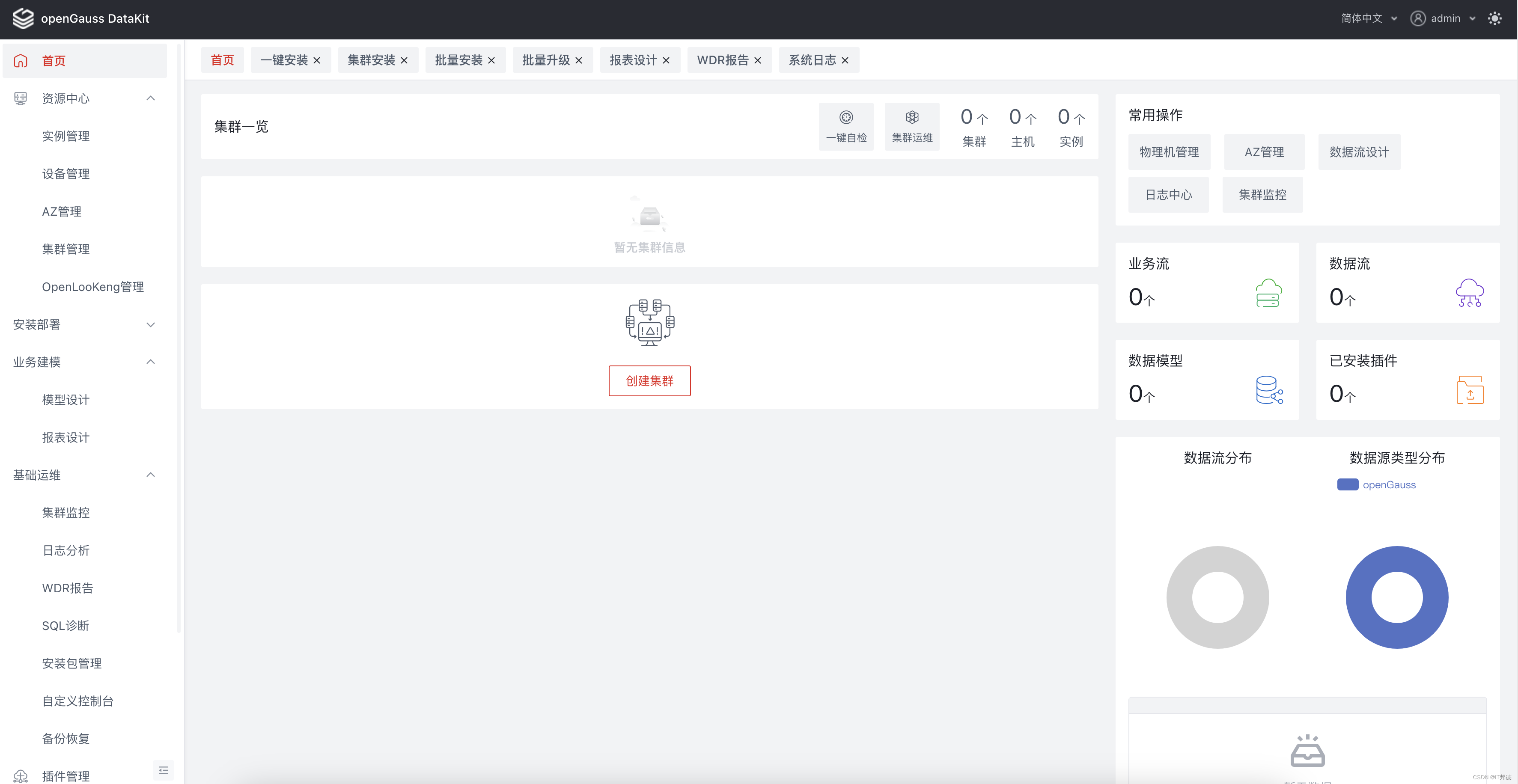
openGaussDatakit让运维如丝般顺滑!
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

整理MongoDB文档:身份验证
整理MongoDB文档:身份验证 个人博客,求关注。 文章概叙 本文主要讲MongoDB在单机状态下的账户配置。理解了MongoDB的语法,对于如何配置用户权限会知道怎么配置,但是请注意给谁配置什么权限才是最重要的。 最小权限原则 系统的每个程序或者…...
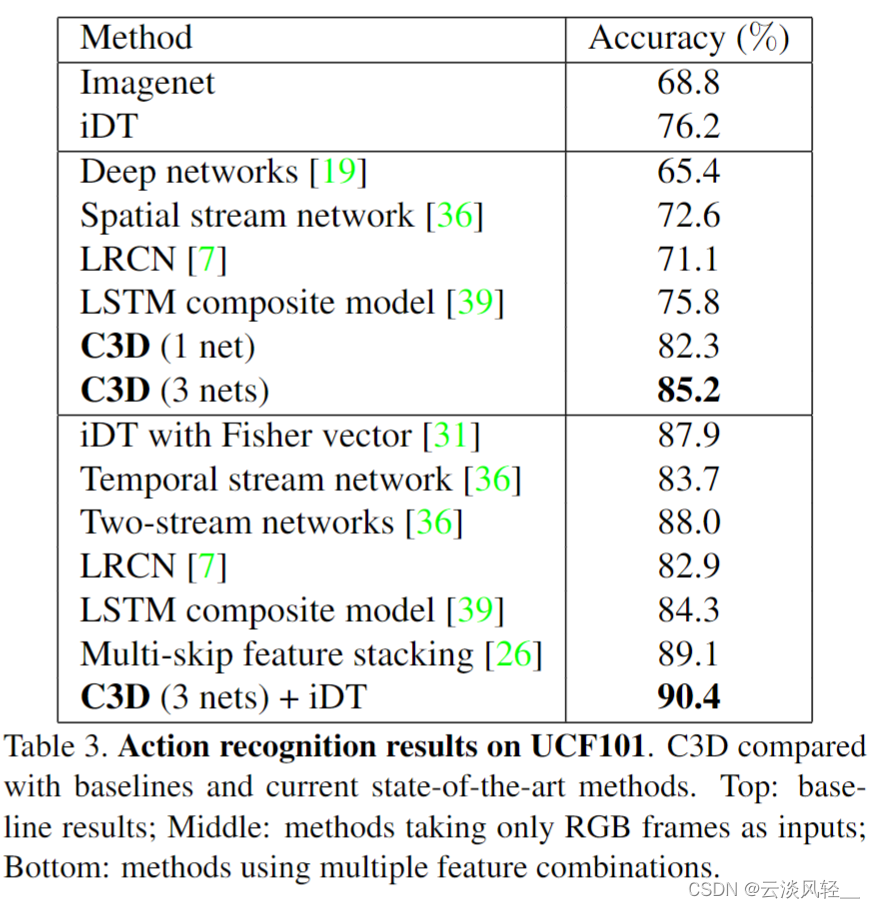
逐字稿 | 视频理解论文串讲(下)【论文精读】
1 为什么研究者这么想把这个双流网络替换掉,想用3D 卷积神经网络来做? 大家好,上次我们讲完了上半部分,就是 2D 网络和一些双流网络以及。它们的。变体。今天我们就来讲一下下半部分,就是 3D 网络和 video Transformer…...

【C++入门:C++世界的奇幻之旅】
1. 什么是C 2. C发展史 3. C的重要性 4. C关键字 5. 命名空间 6. C输入&输出 7. 缺省参数 8. 函数重载 9. 引用 10. 内联函数 11. auto关键字(C11) 12. 基于范围的for循环(C11) 13. 指针空值---nullptr(C11)05. 1. 什么是C C语言是结构化和模块化的语言&…...
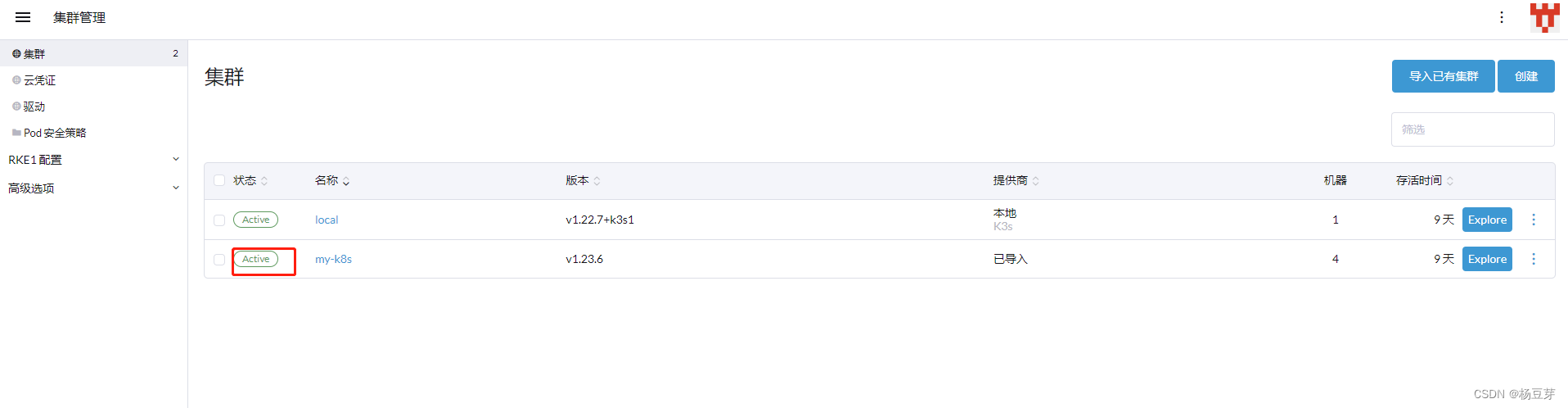
rancher2.6.4配置管理k8s,docker安装
docker快速安装rancher并管理当前k8s集群。 1、拉镜像 docker pull rancher/rancher:v2.6.4 2、启动rancher 启动很慢 --privileged必须拥有root权限,并挂载卷 docker run --privileged -d --restartunless-stopped -p 80:80 -p 443:443 -v /usr/local/docker_vo…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
