球面坐标系下的三重积分
涉及知识点
- 三重积分
- 球面坐标系
- 点火公式
- 一些常见积分处理手法
球面坐标系定义
球面坐标系由方位角φ\varphiφ、仰角θ\thetaθ和距离rrr构成
直角坐标系(x,y,z)(x,y,z)(x,y,z)到球面坐标系的(r,φ,θ)(r,\varphi,\theta)(r,φ,θ)的转化规则如下:
{x=rsinφcosθy=rsinθsinφz=rcosφ\left\{ \begin{aligned} x & = & r\sin φ\cosθ \\ y & = & r\sin θ\sin φ \\ z & = & r\cos φ \end{aligned} \right. ⎩⎨⎧xyz===rsinφcosθrsinθsinφrcosφ

适用
适用于积分区域为球或球的部分、锥或锥的部分。
处理方法
按规则直角坐标系的积分式转换成球面坐标系就行
∭Ωf(x,y,z)dxdydz=∭Ωf(rsinφcosθ,rsinθsinφ,rcosφ)r2sinφdθdφdr\iiint \limits_{\Omega} f(x,y,z)dxdydz=\iiint \limits_{\Omega}f(r\sin φ\cosθ,r\sin θ\sin φ,r\cos φ)r^2\sin \varphi d\theta d\varphi drΩ∭f(x,y,z)dxdydz=Ω∭f(rsinφcosθ,rsinθsinφ,rcosφ)r2sinφdθdφdr
然后一般按如下顺序写出积分式:
∫dθ∫dφ∫f(r,θ,φ)dr\int d\theta \int d\varphi \int f(r,\theta,\varphi)dr∫dθ∫dφ∫f(r,θ,φ)dr
由于“后积先定限”,所以先处理方位角,即下图中1的轨迹,随后处理仰角,即下图中2的轨迹,两个角取值范围都是[0,2π][0,2\pi][0,2π]
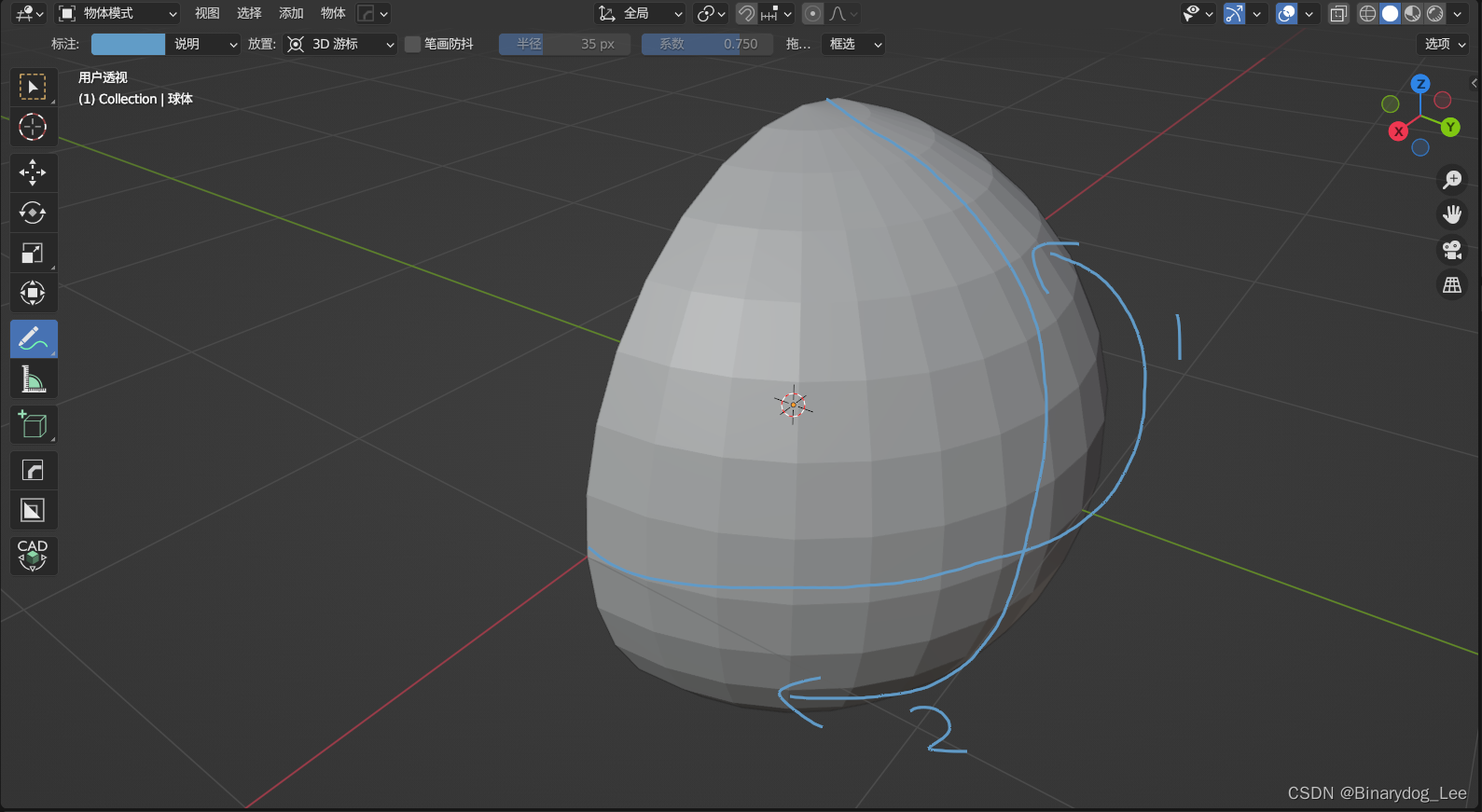
例题
计算三重积分∭Ω(x2+y2)dv\iiint \limits_{\Omega}(x^2+y^2)dvΩ∭(x2+y2)dv其中Ω\OmegaΩ是右半球面x2+y2+z2=a2(y≥0,a>0)x^2+y^2+z^2=a^2\text{ }(y\ge 0,a>0)x2+y2+z2=a2 (y≥0,a>0)与xOzxOzxOz面所围成的区域
【解析】
Ω={0≤r≤a,0≤θ≤π,0≤φ≤π}\Omega = \{0\le r\le a,0\le \theta \le \pi,0\le \varphi \le \pi \}Ω={0≤r≤a,0≤θ≤π,0≤φ≤π}
本题即解如下积分
∭Ωr2sin2φ⋅r2sinφdrdθdφ\iiint \limits_{\Omega}r^2\sin^2\varphi ·r^2\sin \varphi drd\theta d\varphiΩ∭r2sin2φ⋅r2sinφdrdθdφ
即:
∫0πdθ∫0πdφ∫0ar4sin3φdr\int_0^\pi d\theta \int_0^\pi d\varphi \int_0^a r^4\sin^3\varphi dr∫0πdθ∫0πdφ∫0ar4sin3φdr
其中在drdrdr时sin3φ\sin^3\varphisin3φ是常量,可提出,剩下就是对r4r^4r4积分,即变为:
∫0πdθ∫0πsin3φ⋅a55dφ\int_0^\pi d\theta \int_0^\pi \sin^3\varphi · \frac{a^5}{5} d\varphi∫0πdθ∫0πsin3φ⋅5a5dφ
a55\frac{a^5}{5}5a5是常数可提出,并且这个对φ\varphiφ积分完要对θ\thetaθ积分,可以先变换顺序先对θ\thetaθ积分,则原式变为:
π5a3∫0πsin3φdφ\frac{\pi}{5}a^3 \int_0^\pi \sin^3\varphi d\varphi5πa3∫0πsin3φdφ
对于sin3φ\sin^3\varphisin3φ的积分步骤中用到了点火公式,过程如下:
∫0πsin3φdφ=∫0π2sin3φdφ+∫π2πsin3φdφ=23+∫π2πsin3φdφ\int_0^\pi \sin^3\varphi d\varphi=\int_0^{\frac\pi 2} \sin^3\varphi d\varphi+\int_{\frac\pi 2}^\pi \sin^3\varphi d\varphi=\frac23+\int_{\frac\pi 2}^\pi \sin^3\varphi d\varphi∫0πsin3φdφ=∫02πsin3φdφ+∫2ππsin3φdφ=32+∫2ππsin3φdφ
对于右侧的积分继续进行处理,令φ=π−t\varphi = \pi - tφ=π−t(好像算是区间再现公式)
∫π2πsin3φdφ=∫π20sin3(π−t)d(π−t)=∫π20sin3(π−t)d(−t)\int_{\frac\pi 2}^\pi \sin^3\varphi d\varphi=\int_{\frac\pi 2}^0 \sin^3(\pi - t) d(\pi - t)= \int_{\frac\pi 2}^0 \sin^3(\pi - t) d(- t)∫2ππsin3φdφ=∫2π0sin3(π−t)d(π−t)=∫2π0sin3(π−t)d(−t)
提出负号,上下限颠倒,则右侧积分式等于:
∫0π2sin3(π−t)dt\int_0^{\frac\pi 2} \sin^3(\pi - t) dt∫02πsin3(π−t)dt
根据sin3x\sin^3xsin3x的对称性,该式子又等于:
∫0π2sin3tdt=23\int_0^{\frac\pi 2} \sin^3t dt=\frac23∫02πsin3tdt=32
故原式等于
π5a3∫0πsin3φdφ=π5a3⋅(23+23)=415πa5\frac{\pi}{5}a^3 \int_0^\pi \sin^3\varphi d\varphi=\frac{\pi}{5}a^3·(\frac 23+\frac 23)=\frac4{15}\pi a^55πa3∫0πsin3φdφ=5πa3⋅(32+32)=154πa5
即最终结果
相关文章:

球面坐标系下的三重积分
涉及知识点 三重积分球面坐标系点火公式一些常见积分处理手法 球面坐标系定义 球面坐标系由方位角φ\varphiφ、仰角θ\thetaθ和距离rrr构成 直角坐标系(x,y,z)(x,y,z)(x,y,z)到球面坐标系的(r,φ,θ)(r,\varphi,\theta)(r,φ,θ)的转化规则如下: {xrsinφco…...

谷歌 Jason Wei | AI 研究的 4 项基本技能
文章目录 一、前言二、主要内容三、总结CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 原文作者为 Jason Wei,2020 年达特茅斯学院本科毕业,之后加入 Google Brain 工作。 Jason Wei 的博客主页:https://www.jasonwei.net/ 其实我不算是一个特别有经验的研究员…...

excel数据整理:合并计算快速查看人员变动
相信大家平时在整理数据时,都会对比数据是否有重复的地方,或者该数据与源数据相比是否有增加或者减少。数据量不大还好,数据量大的话,对比就比较费劲了。接下来我们将进入数据对比系列课程的学习。该系列一共有两篇教程࿰…...

vit-pytorch实现 MobileViT注意力可视化
项目链接 https://github.com/lucidrains/vit-pytorch 注意一下参数设置: Parameters image_size: int. Image size. If you have rectangular images, make sure your image size is the maximum of the width and heightpatch_size: int. Number of patches. im…...

Python将字典转换为csv
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...
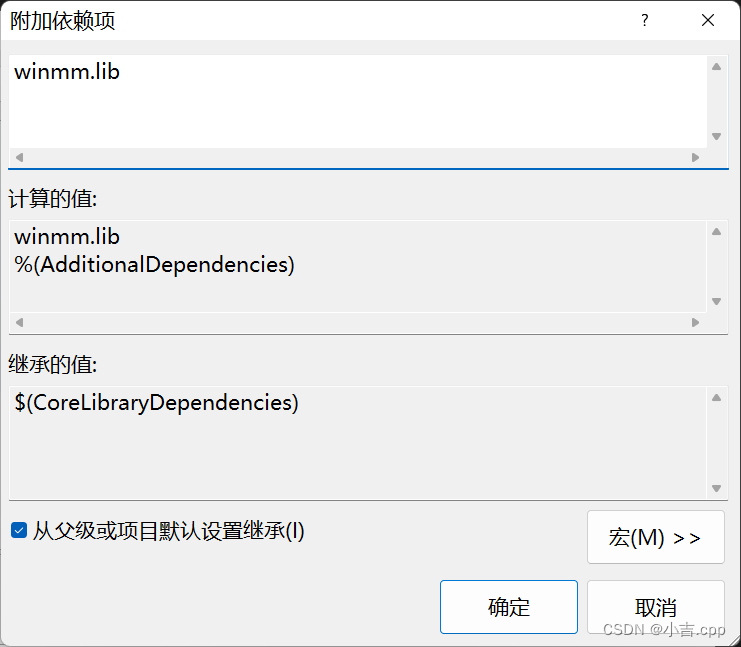
EasyX精准帧率控制打气球小游戏
🎆音乐分享 New Boy —— 房东的猫 之前都用Sleep()来控制画面帧率,忽略了绘制画面的时间 如果绘制画面需要很长的时间,那么就不能忽略了。 并且Sleep()函数也不是特别准确,那么就…...

你知道 GO 中什么情况会变量逃逸吗?
你知道 GO 中什么情况会变量逃逸吗?首先我们先来看看什么是变量逃逸 Go 语言将这个以前我们写 C/C 时候需要做的内存规划和分配,全部整合到了 GO 的编译器中,GO 中将这个称为 变量逃逸 GO 通过编译器分析代码的特征和代码的生命周期&#x…...

一篇文章学懂C++和指针与链表
指针 目录 指针 C的指针学习 指针的基本概念 指针变量的定义和使用 指针的所占的内存空间 空指针和野指针 const修饰指针 指针和数组 指针和函数 指针、数组、函数 接下来让我们开始进入学习吧! C的指针学习 指针的基本概念 指针的作用:可…...

TPGS-cisplatin顺铂修饰维生素E聚乙二醇1000琥珀酸酯
TPGS-cisplatin顺铂修饰维生素E聚乙二醇1000琥珀酸酯(TPGS)溶于大部分有机溶剂,和水有很好的溶解性。 长期保存需要在-20℃,避光,干燥条件下存放,注意取用一定要干燥,避免频繁的溶解和冻干。 维生素E聚乙二醇琥珀酸酯(简称TPGS)是维生素E的水溶性衍生物,由维生素E…...
【20230206-0209】哈希表小结
哈希表一般哈希表都是用来快速判断一个元素是否出现在集合里。哈希函数哈希碰撞--解决方法:拉链法和线性探测法。拉链法:冲突的元素都被存储在链表中线性探测法:一定要保证tableSize大于dataSize,利用哈希表中的空位解决碰撞问题。…...
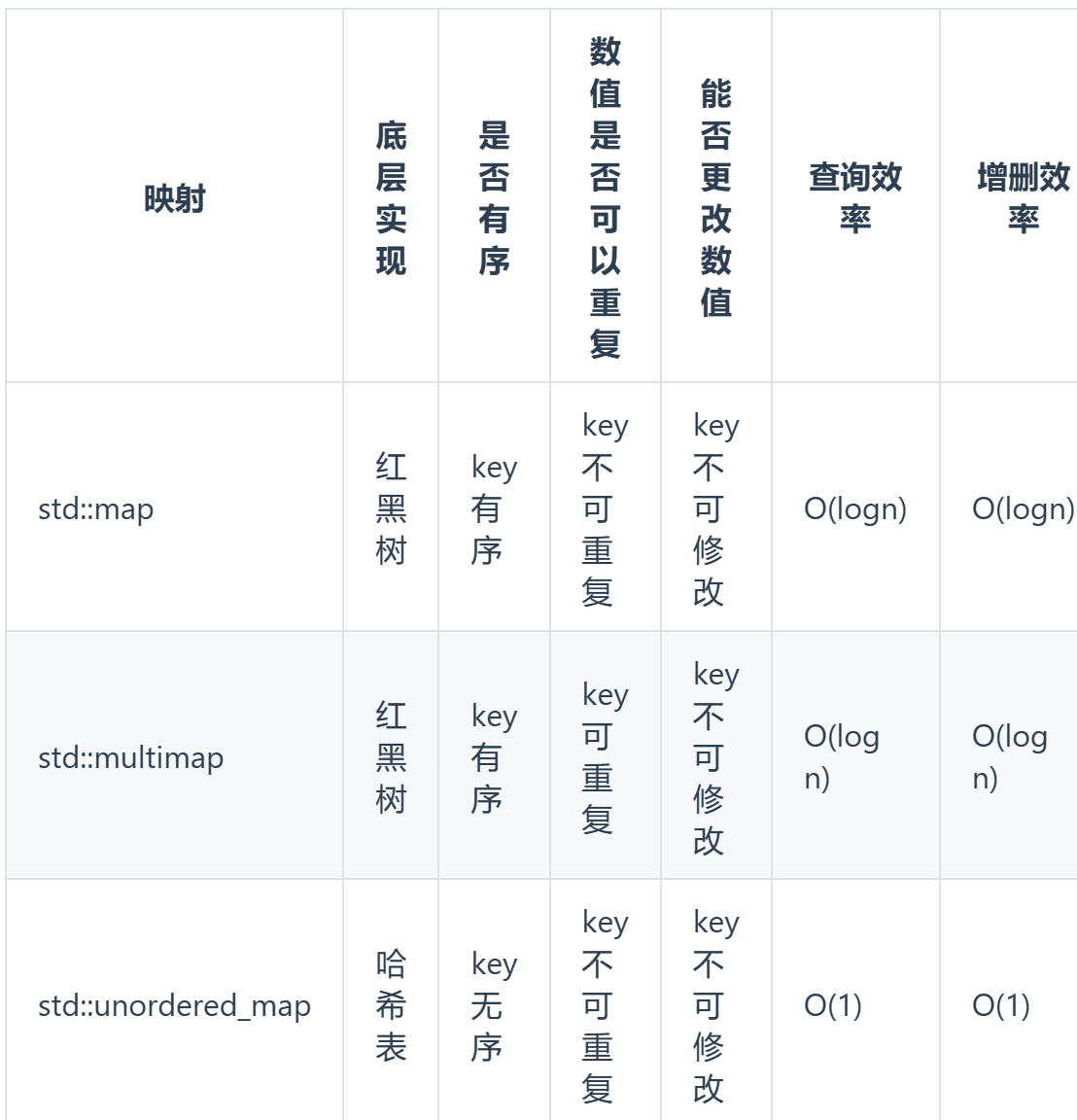
(std::multimap)(一))
c++11 标准模板(STL)(std::multimap)(一)
定义于头文件 <map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class multimap;(1)namespace pmr { template <class Key, class T…...

python进阶——自动驾驶寻找车道
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...
男,26岁,做了一年多的自动化测试,最近在纠结要不要转行,求指点。?
最近一个粉丝在后台问我,啊大佬我现在26了,做了做了一年多的自动化测试,最近在纠结要不要转行,求指点。首选做IT这条路,就是很普通的技术蓝领。对于大部分来说干一辈子问题不大,但是发不了什么财。如果你在…...

源码级别的讲解JAVA 中的CAS
没有CAS之前实现线程安全 多线程环境不使用原子类保证线程安全(基本数据类型) public class T3 {volatile int number 0;//读取public int getNumber(){return number;}//写入加锁保证原子性public synchronized void setNumber(){number;} }多线程环…...

JUC锁与AQS技术【我的Android开发技术】
JUC锁与AQS技术【我的Android开发技术】 AQS原理 AQS就是一个同步器,要做的事情就相当于一个锁,所以就会有两个动作:一个是获取,一个是释放。获取释放的时候该有一个东西来记住他是被用还是没被用,这个东西就是一个状…...

【问题代码】顺序点的深入理解(汇编剖析+手画图解)
这好像是一个哲学问题。 目录 前言 一、顺序点是什么? 二、发生有关顺序点的问题代码 vs中: gcc中: 三、细读汇编 1.vs汇编如下(示例): 2.gcc汇编如下(示例): 四…...
BinaryAI全新代码匹配模型BAI-2.0上线,“大模型”时代的安全实践
导语BinaryAI(https://www.binaryai.net)科恩实验室在2021年8月首次发布二进制安全智能分析平台—BinaryAI,BinaryAI可精准高效识别二进制文件的第三方组件及其版本号,旨在推动SCA(Software Composition Analysis&…...

nvidia设置wifi和接口
tx-nx设置wifi和接口前言基础知识点1.创建和删除一个wifi连接2. 启动连接和关闭连接代码和调试1. 代码展示2. 调试写到最后前言 针对嵌入式开发,有时候通过QT或PAD跨网络对设备设置WIFI,在此记录下,方便后续的查阅。 基础知识点 1.创建和删…...
)
PostgreSQL 变化数据捕捉(CDC)
PostgreSQL 变化数据捕捉(CDC)基于CDC(变更数据捕捉)的增量数据集成总体步骤:1.捕获源数据库中的更改数据2.将变更的数据转换为您的消费者可以接受的格式3.将数据发布到消费者或目标数据库PostgreSQL支持触发器&#x…...

Spring 事务【隔离级别与传播机制】
Spring 事务【隔离级别与传播机制】🍎一.事务隔离级别🍒1.1 事务特性回顾🍒1.2 事务的隔离级别(5种)🍒1.3 事务隔离级别的设置🍎二.Spring 事务传播机制🍒2.1 Spring 事务传播机制的作用🍒2.2 事…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
