【问题代码】顺序点的深入理解(汇编剖析+手画图解)
这好像是一个哲学问题。
目录
前言
一、顺序点是什么?
二、发生有关顺序点的问题代码
vs中:
gcc中:
三、细读汇编
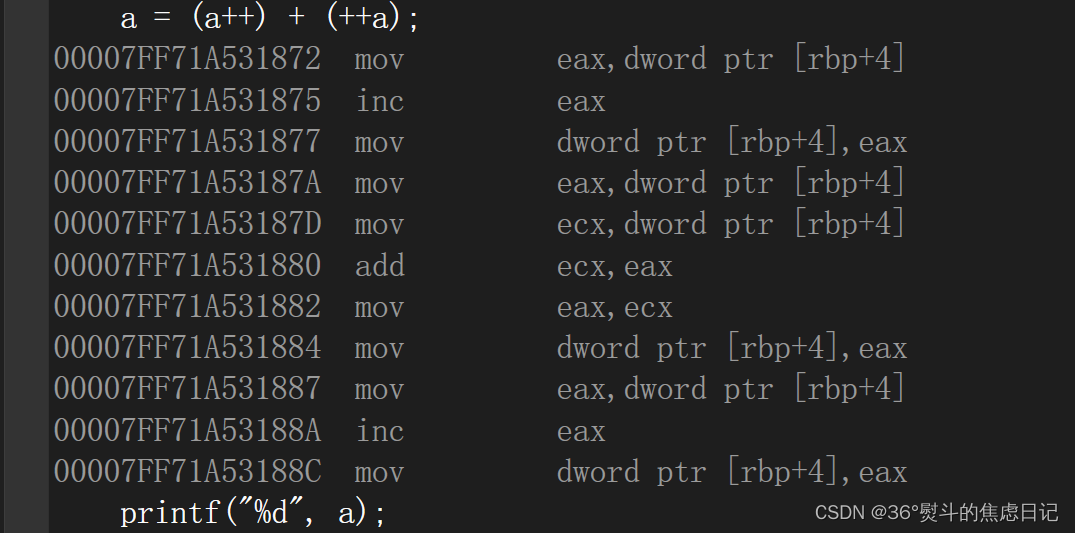
1.vs汇编如下(示例):
2.gcc汇编如下(示例):
四、理解汇编
图解
原因:
五、如果是a = (++a) + (++a)呢?
1.vs汇编:
2.图解:
总结
前言
一旦执行到一个顺序点,此前的副作用都必须生效。
一、顺序点是什么?
顺序点,也称作序列点,是计算机程序中一些执行点,在该点处之前的求值的所有的副作用已经发生,在它之后的求值的所有副作用仍未开始。在C与C++程序设计语言中,表达式的值依赖于它的子表达式的求值顺序。增加更多的顺序点限制了可能的求值顺序,能保证有一个一致结果。(来源:百度百科)
二、发生有关顺序点的问题代码
代码如下(示例):
#include <stdio.h>int main()
{int a = 0;a = (a++) + (++a);printf("%d", a);return 0;
}a++的副作用是将a增加了a,按照以往的常识是在这句话结束后才会产生此副作用,但是这时表达式左边也是a,a到底是在这句话结束后才产生的副作用还是一边向后执行,一边产生副作用?(哲学吗)
这个就取决于编译器了,这也正是这段代码的问题所在。
vs中:
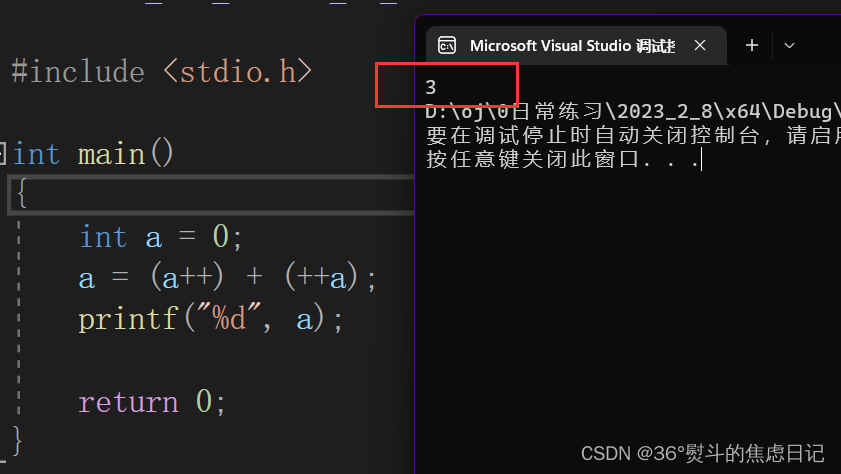
gcc中:

三、细读汇编
1.vs汇编如下(示例):
2.gcc汇编如下(示例):
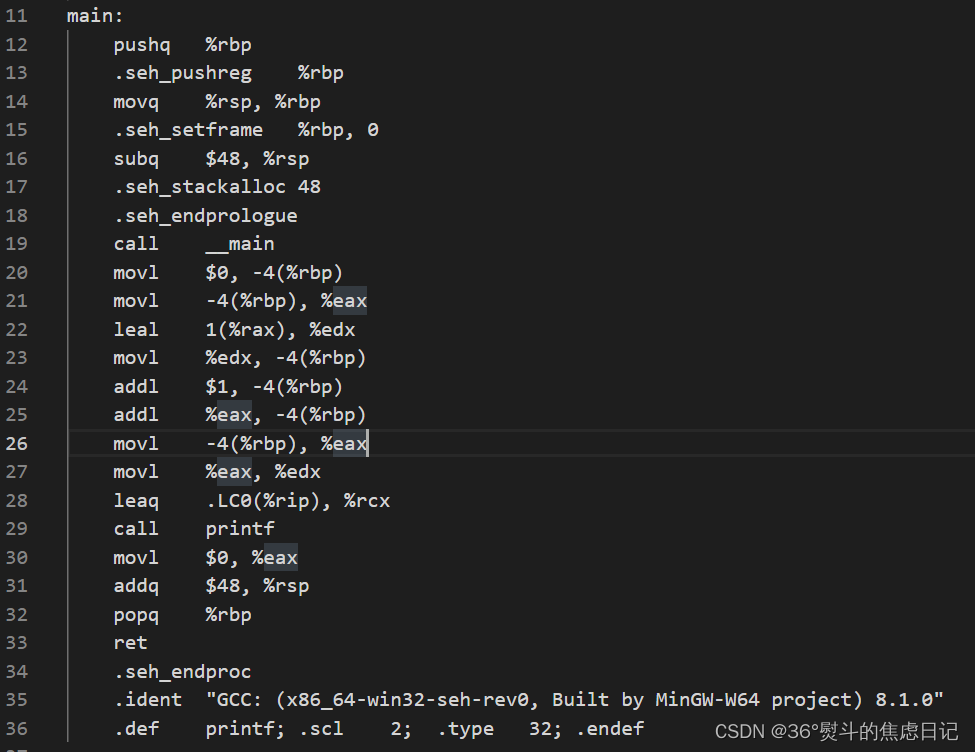
四、理解汇编
汇编的人话版就是:
①前置++优先级略高于后置++,先算前置的,
②算出来以后因为表达式左边也有a,前置++这个式子对于其有副作用,就去更新左值a,a = 1
③更新好后,再来计算a++
④因为后置++是先赋值后计算,所以在后置++中,a是前置++算出来以后的值,所以计算后置++后,a没有发生变化,不用更新a(a = 1)
⑤两个++都算完以后,该算“+”了,此时计算的式子是:1+1 = 2;2是表达式右边的值,其等于表达式左边,左边是a,所以此时a = 2
⑥此时该后置++运算了,取得a的最新值为2,进行++,得到a的最终值是3。
图解
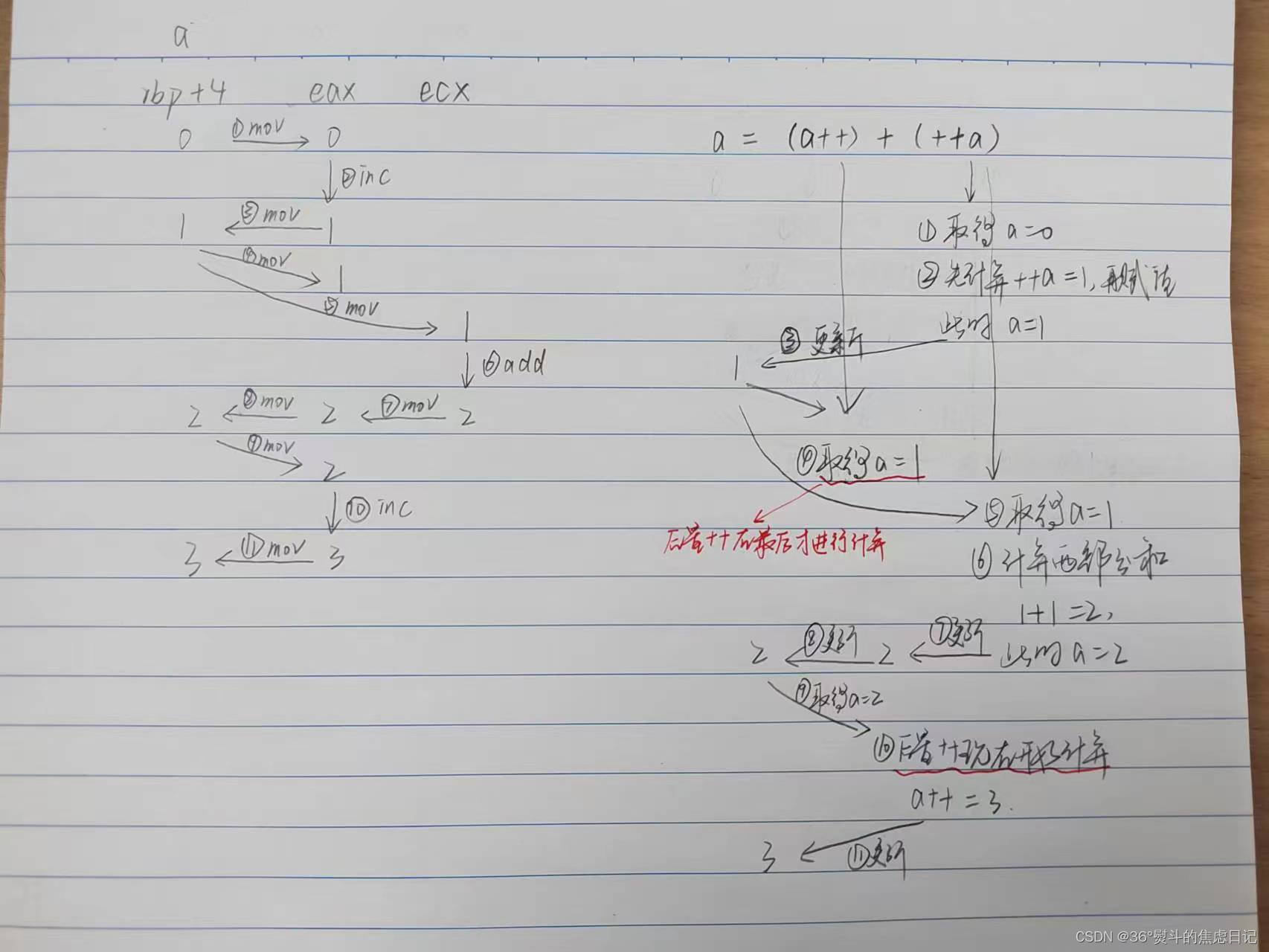
原因:
所以,当有副作用式子出现时,如果还写了一段问题代码,那么这个时候就需要看编译器对于顺序点前后的处理方式,vs与gcc也正是因此而产生的不同答案。
五、如果是a = (++a) + (++a)呢?
与四分析方式相同,结论是:
先算出所有的副作用带来的影响(++),再计算没有副作用的式子(+)。
1.vs汇编:
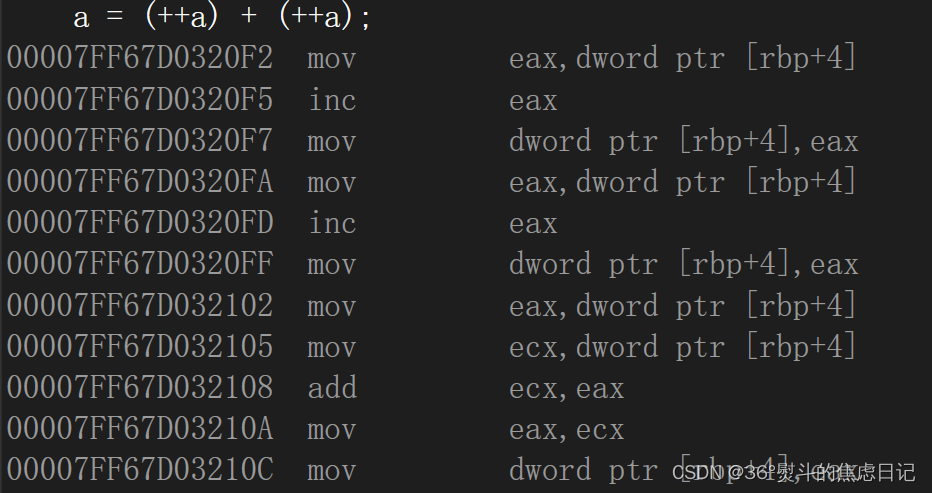
2.图解:

总结
- 表达式如果不能通过操作符的属性确定唯一的计算路径,表达式就是存在问题的。
- 尽量少写产生顺序点疑问的代码。
相关文章:

【问题代码】顺序点的深入理解(汇编剖析+手画图解)
这好像是一个哲学问题。 目录 前言 一、顺序点是什么? 二、发生有关顺序点的问题代码 vs中: gcc中: 三、细读汇编 1.vs汇编如下(示例): 2.gcc汇编如下(示例): 四…...
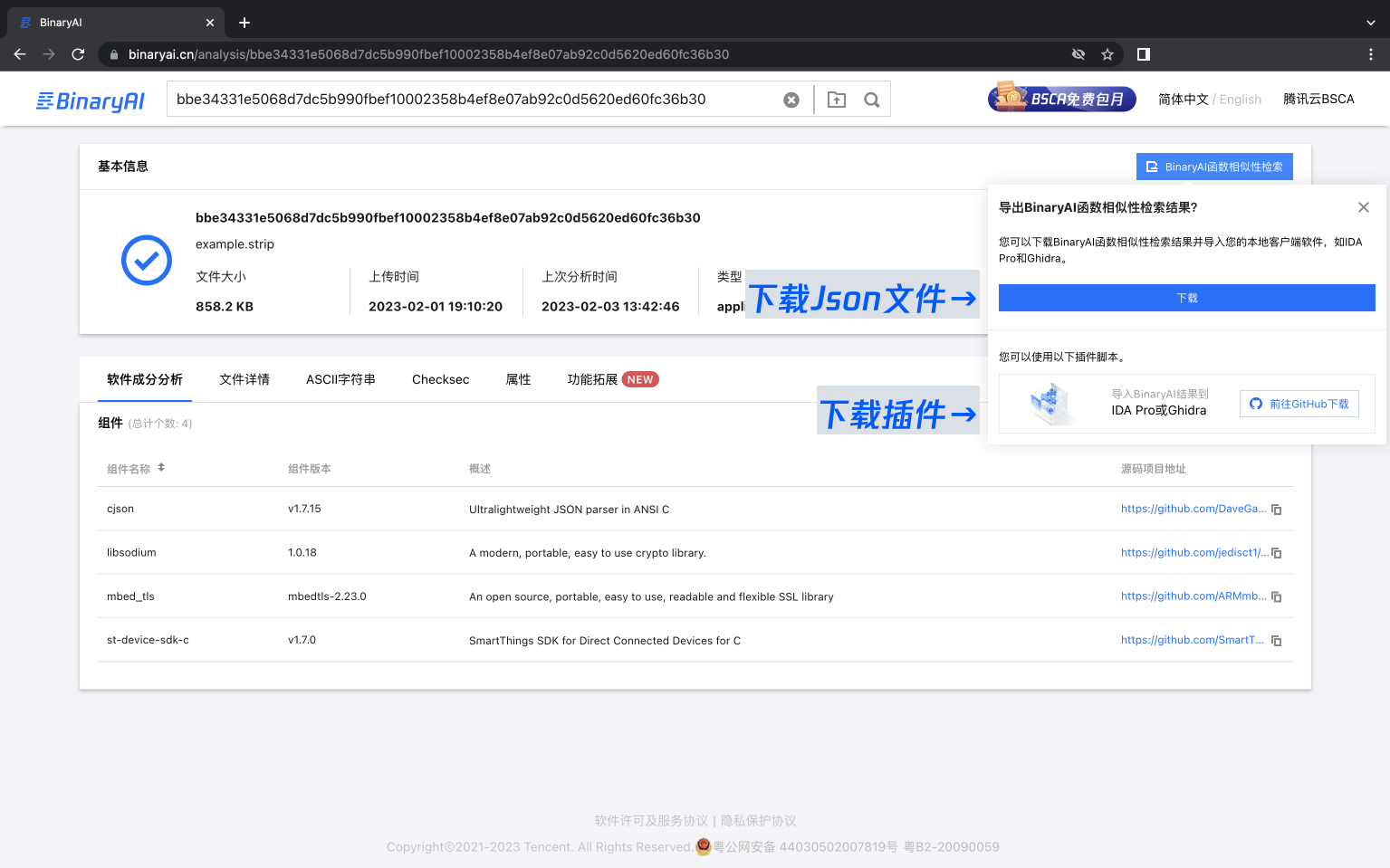
BinaryAI全新代码匹配模型BAI-2.0上线,“大模型”时代的安全实践
导语BinaryAI(https://www.binaryai.net)科恩实验室在2021年8月首次发布二进制安全智能分析平台—BinaryAI,BinaryAI可精准高效识别二进制文件的第三方组件及其版本号,旨在推动SCA(Software Composition Analysis&…...

nvidia设置wifi和接口
tx-nx设置wifi和接口前言基础知识点1.创建和删除一个wifi连接2. 启动连接和关闭连接代码和调试1. 代码展示2. 调试写到最后前言 针对嵌入式开发,有时候通过QT或PAD跨网络对设备设置WIFI,在此记录下,方便后续的查阅。 基础知识点 1.创建和删…...
)
PostgreSQL 变化数据捕捉(CDC)
PostgreSQL 变化数据捕捉(CDC)基于CDC(变更数据捕捉)的增量数据集成总体步骤:1.捕获源数据库中的更改数据2.将变更的数据转换为您的消费者可以接受的格式3.将数据发布到消费者或目标数据库PostgreSQL支持触发器&#x…...

Spring 事务【隔离级别与传播机制】
Spring 事务【隔离级别与传播机制】🍎一.事务隔离级别🍒1.1 事务特性回顾🍒1.2 事务的隔离级别(5种)🍒1.3 事务隔离级别的设置🍎二.Spring 事务传播机制🍒2.1 Spring 事务传播机制的作用🍒2.2 事…...
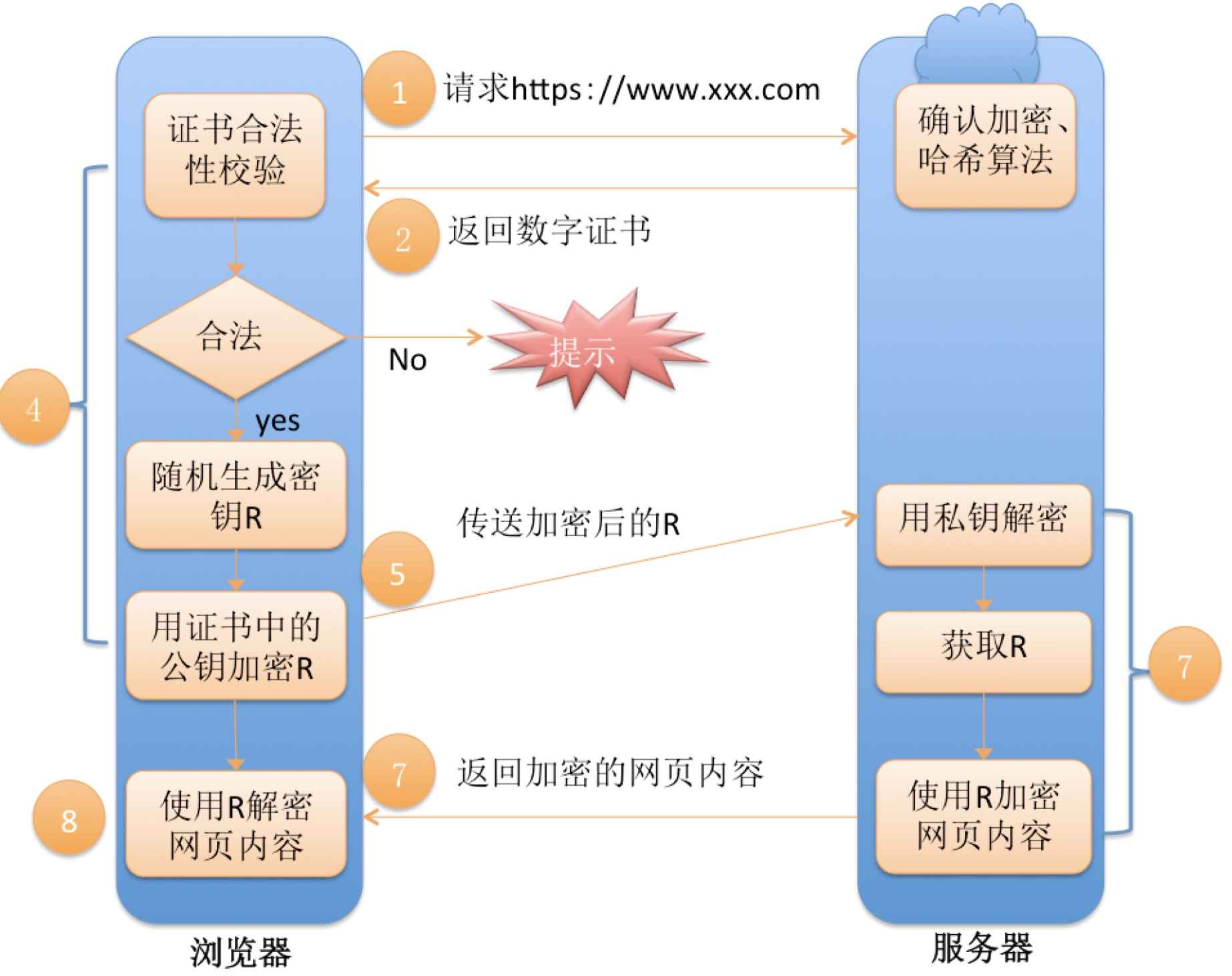
HTTP和HTTPS协议
HTTP协议 HTTP协议是一种应用层的协议,全称为超文本传输协议。 URL URL值统一资源定位标志,也就是俗称的网址。 协议方案名 http://表示的就是协议方案名,常用的协议有HTTP协议、HTTPS协议、FTP协议等。HTTPS协议是以HTTP协议为基础&#…...
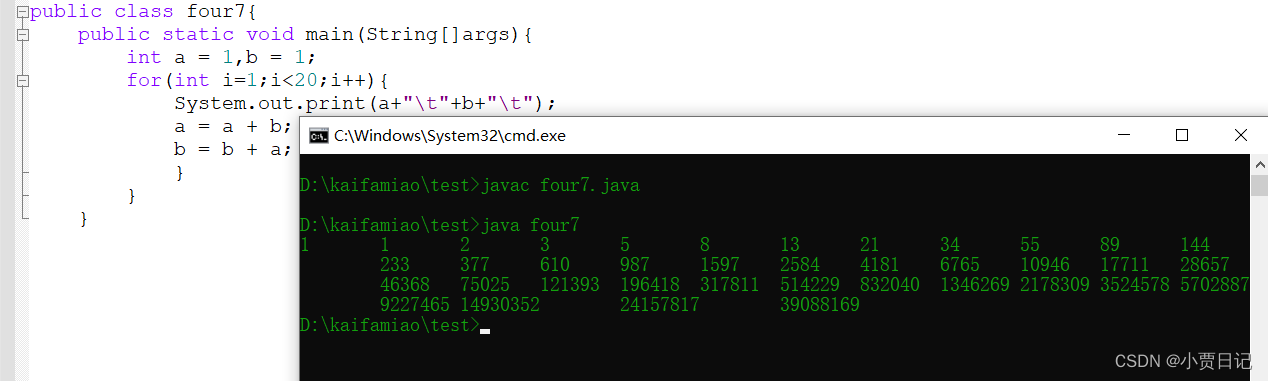
day3——有关java运算符的笔记
今天主要学习的内容有java的运算符 赋值运算符算数运算符关系运算符逻辑运算符位运算符(专门写一篇笔记)条件运算符运算符的优先级流程控制 赋值运算符 赋值运算符()主要用于给变量赋值,可以跟算数运算符相结合&…...
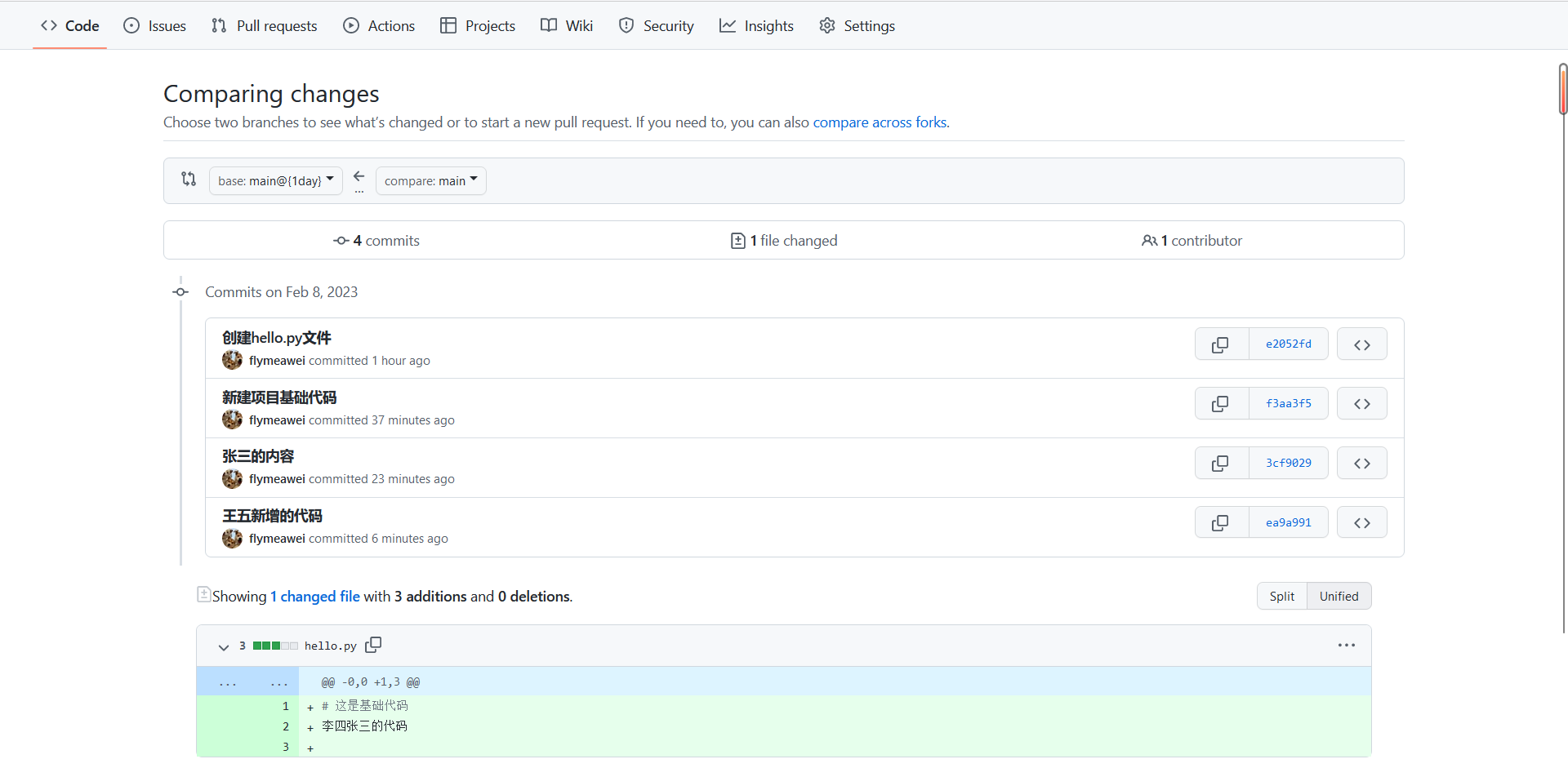
Git多人协同远程开发
1. 李四(项目负责人)操作步骤 在github中创建远程版本库testgit将基础代码上传⾄testgit远程库远程库中基于main分⽀创建dev分⽀将 githubleaflife/testgit 共享给组员李四继续在基础代码上添加⾃⼰负责的模块内容 2. 张三、王五(组员&…...

Chapter4:机器人仿真
ROS1{\rm ROS1}ROS1的基础及应用,基于古月的课,各位可以去看,基于hawkbot{\rm hawkbot}hawkbot机器人进行实际操作。 ROS{\rm ROS}ROS版本:ROS1{\rm ROS1}ROS1的Melodic{\rm Melodic}Melodic;实际机器人:Ha…...
python(14)--集合
前言 本篇文章学习的是 python 中集合的基础知识。 集合元素的内容是不可变的,常见的元素有整数、浮点数、字符串、元组等。至于可变内容列表、字典、集合等不可以是集合元素。虽然集合不可以是集合的元素,但是集合本身是可变的,可以去增加或…...

【Spark分布式内存计算框架——Spark Core】4. RDD函数(中)Transformation函数、Action函数
3.2 Transformation函数 在Spark中Transformation操作表示将一个RDD通过一系列操作变为另一个RDD的过程,这个操作可能是简单的加减操作,也可能是某个函数或某一系列函数。值得注意的是Transformation操作并不会触发真正的计算,只会建立RDD间…...
Mysql 数据类型
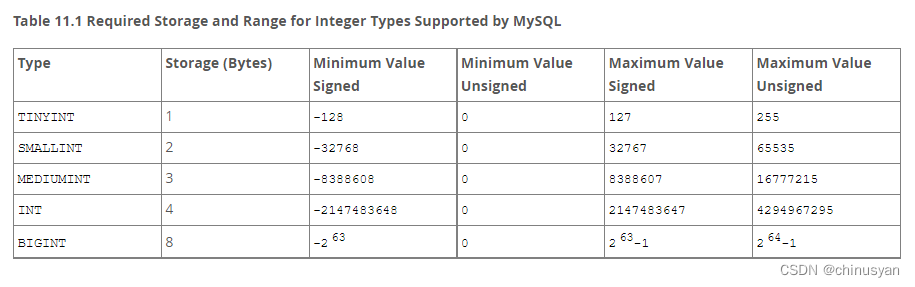
1、数值数据类型 1.1 整数类型(精确值) INTEGER, INT, SMALLINT, TINYINT, MEDIUMINT, BIGINT MySQL支持SQL标准的整数类型INTEGER (或INT)和SMALLINT。作为标准的扩展,MySQL还支持整数类型TINYINT、MEDIUMINT和BIGINT。下表显示了每种整数类型所需的存储和范围。…...

运行Whisper笔记(1)
最近chatGPT很火,就去逛了一下openai的github项目。发现了这个项目。 这个项目可以识别视频中的音频,转换出字幕。 带着一颗好奇的心就尝试自己去部署玩一玩 跟着这篇文章一步步来进行安装,并且跟着这篇文章解决途中遇到的问题。 途中还会遇…...
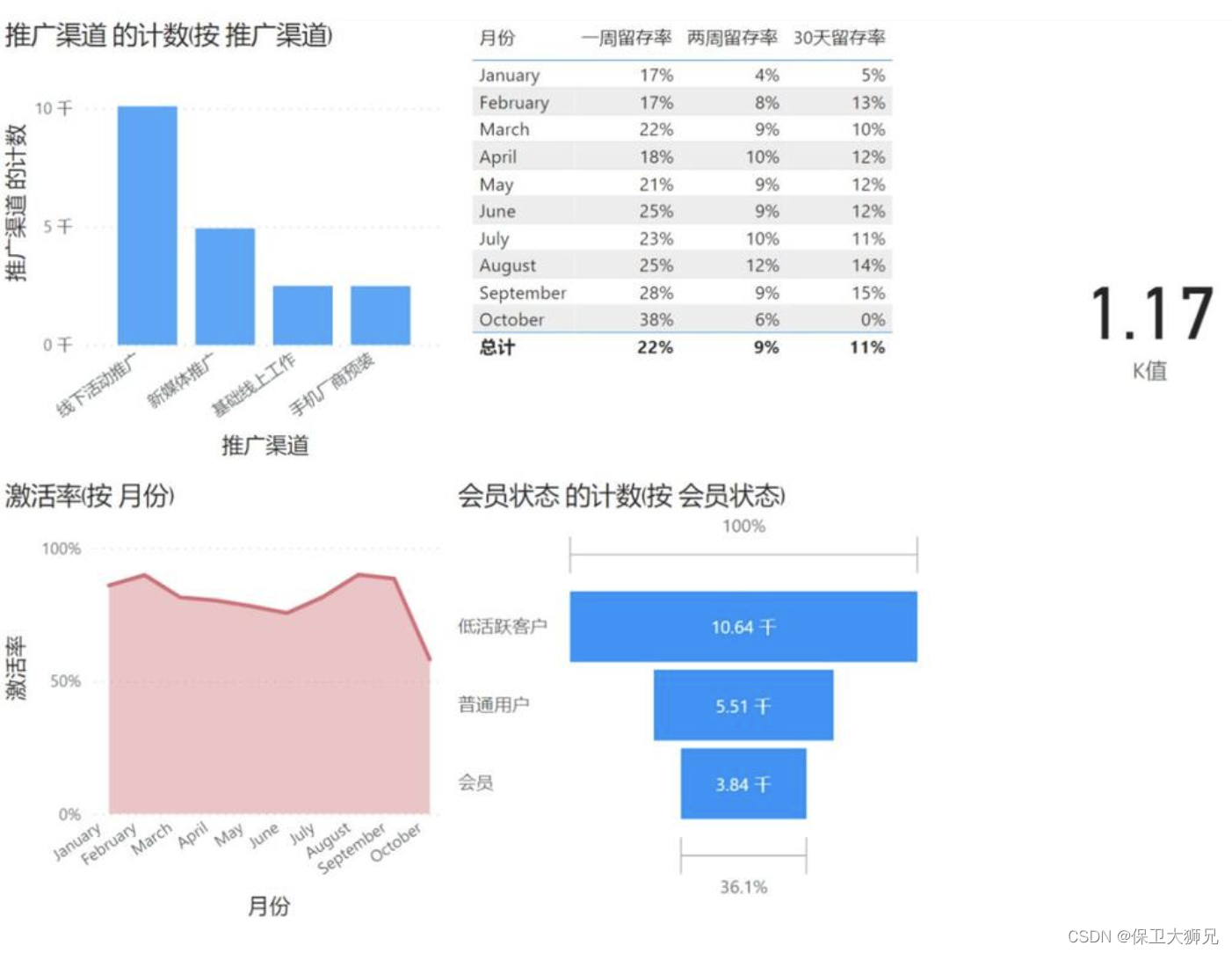
2023年最强大的12款数据可视化工具,值得收藏
做数据分析也有年头了,好的坏的工具都用过,推荐几个觉得很好用的,避坑必看! PS:一般比较成熟的公司里,数据分析工具不只是满足业务分析和报表制作,像我现在给我们公司选型BI工具,是做…...

LeetCode刷题系列 -- 523. 连续的子数组和
给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:子数组大小 至少为 2 ,且子数组元素总和为 k 的倍数。如果存在,返回 true ;否则,返回 false 。如果存…...

LeetCode刷题系列 -- 525. 连续数组
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。示例 1:输入: nums [0,1]输出: 2说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。示例 2:输入: nums [0,1,0]输出: 2说明: [0, 1] (或 [1, 0]) 是具有相同数…...
JavaEE15-Spring Boot统一功能处理
目录 1.统一用户登录权限效验 1.1.最初用户登录验证 1.2.Spring AOP用户统一登录验证的问题 1.3.Spring拦截器 1.3.1.创建自定义拦截器,实现 HandlerInterceptor 接口并重写 preHandle(执行具体方法之前的预处理)方法 1.3.2.将自定义拦…...
centos7.6 设置防火墙
1、查看系统版本 cat /etc/redhat-release2、查看防火墙运行状态 systemctl status firewalld这里可以看到当前是未运行状态(inactive)。 3、关闭开机自启动防火墙 systemctl disable firewalld.service4、启动防火墙并查看状态,系统默认 22 端口是开启的。 sy…...
在线支付系列【22】微信支付实战篇之集成服务商API
有道无术,术尚可求,有术无道,止于术。 文章目录前言1. 环境搭建2. 特约商户进件3. 统一下单总结前言 在上篇文档中,我们做好了接入前准备工作,接下来使用开源框架集成服务商相关API。 一个简单的支付系统完成支付流程…...

3.2 埃尔米特转置
定义 对于复矩阵,转置又不一样,常见的操作是共轭转置,也叫埃尔米特转置Hermitian transpose。埃尔米特转置就是对矩阵先共轭,再转置,一般来说用三种符号表示埃尔米特转置: 第一种符号是AHA^HAH,…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...