3.2 埃尔米特转置
定义
对于复矩阵,转置又不一样,常见的操作是共轭转置,也叫埃尔米特转置Hermitian transpose。埃尔米特转置就是对矩阵先共轭,再转置,一般来说用三种符号表示埃尔米特转置:
- 第一种符号是AHA^HAH,这是国内教材通用的做法,H是埃尔米特名字首字母;
- 第二种符号是A∗A^*A∗,这是国外教材喜欢用,这个符号在国内教材表示伴随矩阵,如以下文档:

- 第三种符号是匕首符号A†A^{\dagger}A†,但是有时候也用来表示矩阵的加号逆。
求埃尔米特转置的代码比较简单,python就一行代码:
# 埃尔米特转置def hermitian_transpose(self):return Matrix([[e.conjugate() for e in v] for v in self.__vectors]).transpose_matrix()
测试了一个矩阵:
(1−i6−i2−8i2+i5+i4−i)H=(1+i2−i6+i5−i2+8i4+i)\begin{pmatrix}1-i & 6-i & 2-8i\\ 2+i & 5+i & 4-i\\ \end{pmatrix}^H= \begin{pmatrix}1+i & 2-i\\ 6+i & 5-i\\ 2+8i & 4+i\\ \end{pmatrix} (1−i2+i6−i5+i2−8i4−i)H=1+i6+i2+8i2−i5−i4+i
埃尔米特阵
如果一个矩阵,埃尔米特转置后还是它自己,这样的矩阵就是埃尔米特阵。毫无疑问,矩阵必须得是一个方阵。所以它的判断方式也很简单,首先判断是否为方阵,再以对角线为对称轴判断就完事了,但是要注意数据类型,把复数和其他类型区分开来,所以代码会稍微长一点:
# 是否埃尔米特阵def is_hermitian(self):m = len(self.__vectors[0])n = len(self.__vectors)if m != n:return False# 遍历每一行对角线以上的元素for i in range(m):for j in range(i+1, n):e = self.__vectors[j][i]f = self.__vectors[i][j]if isinstance(e, complex):if e != f.conjugate():return Falseelse:if e != f:return Falsereturn True
比如以下矩阵就是一个埃尔米特阵:
(1−i2−i3+i2+i5+i3+i3−i3−i3−i)\begin{pmatrix}1-i & 2-i & 3+i\\ 2+i & 5+i & 3+i\\ 3-i & 3-i & 3-i\\ \end{pmatrix} 1−i2+i3−i2−i5+i3−i3+i3+i3−i
酉矩阵
一个方阵的逆矩阵恰好是自己的埃尔米特转置,这样的矩阵被称为酉矩阵unitary matrix,也就是:
AAH=AHA=IAA^H=A^HA=I AAH=AHA=I
AAH=AHAAA^H=A^HAAAH=AHA这个定义就限制了必须为方阵。所以它的判断也比较简单:
# 是否为酉矩阵def is_unitary(self):m = len(self.__vectors[0])n = len(self.__vectors)if m != n:return Falsex = self * self.hermitian_transpose()return x.is_identity()# 是否为单位矩阵def is_identity(self):m = len(self.__vectors[0])n = len(self.__vectors)if m != n:return Falsefor i in range(n):for j in range(n):if i == j:if self.__vectors[i][j] != 1:return Falseelif self.__vectors[i][j] != 0:return Falsereturn True
比如以下两个矩阵就是一个酉矩阵:
(0.5−0.5i−0.5+0.5i0.5i0.50.5+0.5i0.5+0.5i−0.5+0.5i0)(0.5−0.5i0.5−0.5i0.5i0.5−0.5−0.5i−0.5−0.5i0.5−0.5i0)=(100010001)\begin{pmatrix}0.5 & -0.5i & -0.5+0.5i\\ 0.5i & 0.5 & 0.5+0.5i\\ 0.5+0.5i & -0.5+0.5i & 0\\ \end{pmatrix}\begin{pmatrix}0.5 & -0.5i & 0.5-0.5i\\ 0.5i & 0.5 & -0.5-0.5i\\ -0.5-0.5i & 0.5-0.5i & 0\\ \end{pmatrix}\\=\begin{pmatrix}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix} 0.50.5i0.5+0.5i−0.5i0.5−0.5+0.5i−0.5+0.5i0.5+0.5i00.50.5i−0.5−0.5i−0.5i0.50.5−0.5i0.5−0.5i−0.5−0.5i0=100010001
相关文章:

3.2 埃尔米特转置
定义 对于复矩阵,转置又不一样,常见的操作是共轭转置,也叫埃尔米特转置Hermitian transpose。埃尔米特转置就是对矩阵先共轭,再转置,一般来说用三种符号表示埃尔米特转置: 第一种符号是AHA^HAH,…...
Python爬虫之Scrapy框架系列(13)——实战ZH小说爬取数据入MySql数据库
目录:1 数据持久化存储,写入Mysql数据库①定义结构化字段:②重新编写爬虫文件:③编写管道文件:④辅助配置(修改settings.py文件):⑤navicat创库建表:⑥ 效果如下…...
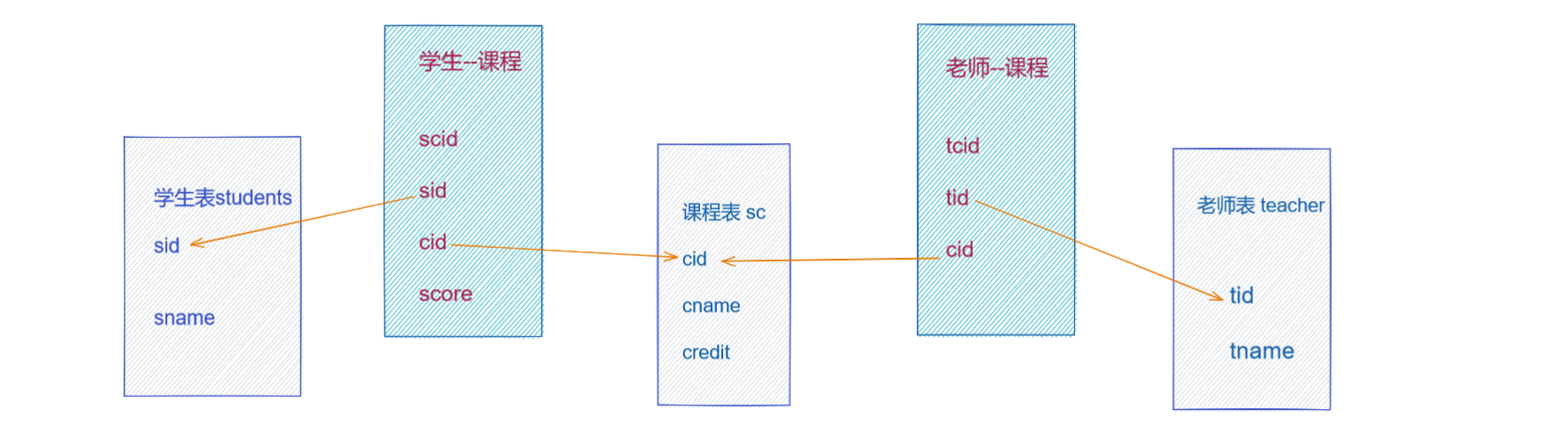
MySQL篇02-三大范式,多表查询
数据入库时,由于数据设计不合理,会存在数据重复、更新插入异常等情况, 故数据库中表的设计遵循的设计规范:三大范式1.第一范式(1NF)要求数据库的每一列都是不可分割的原子数据项,即原子性。强调的是列的原子性,即数据库中每一列的…...

vue-cli3创建Vue项目
文章目录前言一、使用vue-cli3创建项目1.检查当前vue的版本2.下载并安装Vue-cli33.使用命令行创建项目二、关于配置前言 本文讲解了如何使用vue-cli3创建属于自己的Vue项目,如果本文对你有所帮助请三连支持博主,你的支持是我更新的动力。 下面案例可供…...
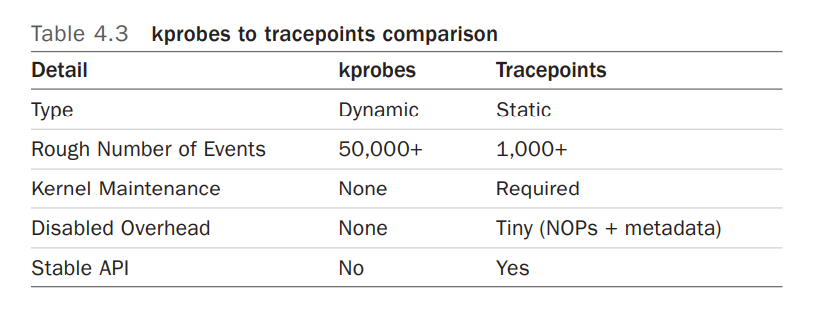
Linux perf probe 的使用(三)
文章目录前言一、Dynamic Tracing二、kprobes2.1 perf kprobe 的使用2.2 kprobe Arguments3.3 tcp_sendmsg()3.3.1 Kernel: tcp_sendmsg()3.3.2 Kernel: tcp_sendmsg() with size3.3.2 Kernel: tcp_sendmsg() line number and local variable三、uprobes的使用3.1 perf uprobe …...

python GUI编程 多窗口跳转
# 多窗口跳转例子from tkinter import *def main(): # 主窗体def goto(num):root.destroy() # 关闭主窗体if num 1:one() # 进入第1个窗体elif num 2:two() # 进入第2个窗体root Tk()root.geometry(300x150600200)root.title(登录窗口)but1 Button(root, text"进入…...
nuxt 学习笔记
这里写目录标题路由跳转NuxtLinkquery参数params参数嵌套路由tab切换效果layouts 文件夹强制约定放置所有布局文件,并以插槽的形式作用在页面中1.在app.vue里面2.component 组件使用Vue < component :is"">Vuex生命周期数据请求useFetchuseAsyncDat…...
Python编程自动化办公案例(1)
作者简介:一名在校计算机学生、每天分享Python的学习经验、和学习笔记。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.使用库讲解 1.xlrd 2.xlwt 二.主要案例 1.批量合并 模板如下…...
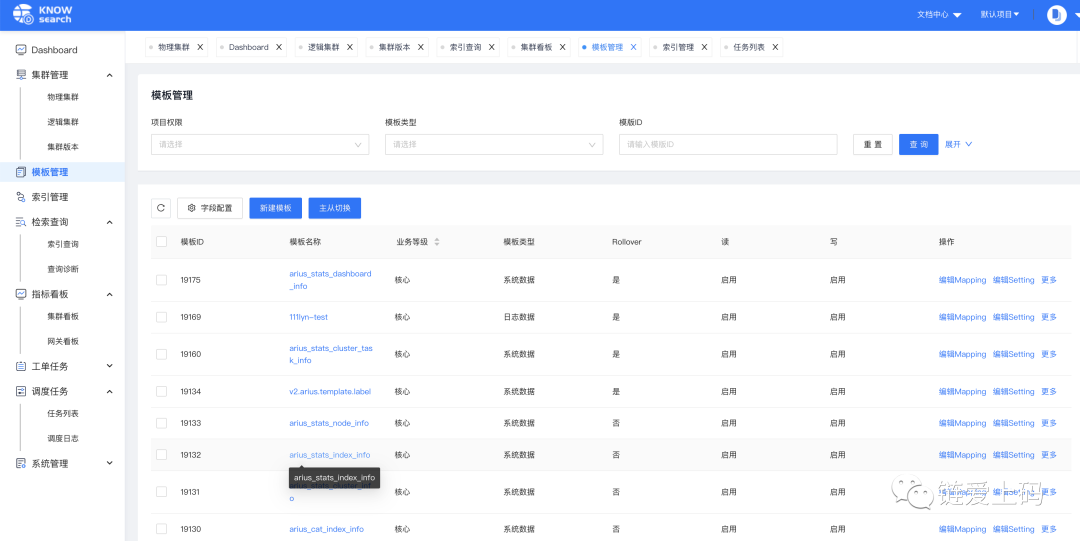
一站式 Elasticsearch 集群指标监控与运维管控平台
上篇文章写了一下消息运维管理平台,今天带来的是ES的监控和运维平台。目前初创企业,不像大型互联网公司,可以重复的造轮子。前期还是快速迭代试错阶段,方便拿到市场反馈,及时调整自己的战略和产品方向。让自己活下去&a…...

C# 调用Python
一、简介 IronPython 是一种在 NET 和 Mono 上实现的 Python 语言,由 Jim Hugunin(同时也是 Jython 创造者)所创造。 Python是一种跨平台的计算机程序设计语言。 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。 Python是…...
)
51单片机最强模块化封装(3)
文章目录 前言一、创建smg文件,添加smg文件路径二、smg文件编写三、模块化测试总结前言 本篇文章将带大家继续封装我们的代码。 这里我们会封装数码管的操作函数。 一、创建smg文件,添加smg文件路径 这里的操作就不过多解释了,大家自行看前面的文章即可。 51单片机模块化…...

【CSS 布局】水平垂直居中
CSS 布局-水平垂直居中 一、水平居中 创建一个父盒子,和子盒子 <div class"parent"><div class"child"></div> </div>基本样式如下 .parent {background-color: #fff; }.child {background-color: #999;width: 100p…...

【C++】类和对象--类的6个默认成员函数
目录1.类的6个默认成员函数2.构造函数2.1概念2.2特性3.析构函数3.1概念3.2特性4.拷贝构造函数4.1概念4.2特征5.赋值运算符重载5.1运算符重载5.2赋值运算符重载5.3前置和后置重载5.4流插入和流提取运算符重载6.const成员7.取地址重载和const取地址操作符重载1.类的6个默认成员函…...

常见面试题---------如何处理MQ消息丢失的问题?
如何处理MQ消息丢失的问题? RabbitMQ丢失消息分为如下几种情况: 生产者丢消息: 生产者将数据发送到RabbitMQ的时候,可能在传输过程中因为网络等问题而将数据弄丢了。 RabbitMQ自己丢消息: 如果没有开启RabbitMQ的持久化&#x…...

十四、Linux网络:高级IO
目录 五种IO模型 同步IO 阻塞IO 非阻塞IO 信号驱动IO IO多路转接 异步IO...

带你走进API安全的知识海洋
Part1什么是API API(Application Programming Interface,应用程序接口)是一些预先定义的接口(如函数、HTTP接口),或指软件系统不同组成部分衔接的约定。用来提供应用程序与开发人员基于某软件或硬件得以访…...
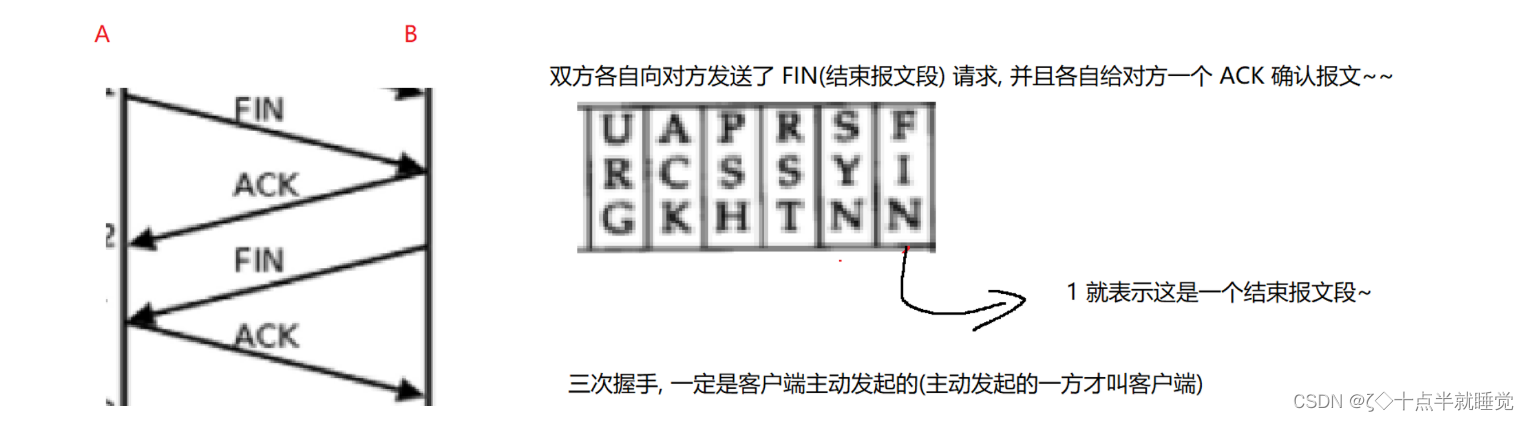
【Java】TCP的三次握手和四次挥手
三次握手 TCP三次握手是一个经典的面试题,它指的是TCP在传递数据之前需要进行三次交互才能正式建立连接,并进行数据传递。(客户端主动发起的)TCP之所以需要三次握手是因为TCP双方都是全双工的。 什么是全双工? TCP任何…...

JUC并发编程
1.什么是JUC java.util工具包、包、分类 业务:普通业务线程代码 Thread Runable: 没有返回值、效率相比Callable相对较低。 2.线程和进程 进程:一个程序,QQ.exe Music.exe 程序的集合 一个进程往往可以包含多个线程,至少包含一个…...

概率统计·假设检验【正态总体均值的假设检验、正态总体方差的假设检验】
均值假设检验定义 2类错误 第1类错误(弃真):当原假设H0为真,观察值却落入拒绝域,因而拒 绝H0这类错误是“以真为假” 犯第一类错误的概率显著性水平α第2类错误(取伪):当原假设H0不…...

如何预测机组设备健康状态?你可能需要这套解决方案
1. 应用场景随机振动[注1]会发生在工业物联网的各个场景中,包括产线机组设备的运行、运输设备的移动、试验仪器的运行等等。通过分析采集到的振动信号可以预估设备的疲劳年限、及时知晓设备已发生的异常以及预测未来仪器可能发生的异常等等。本篇教程会提供给有该方…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
