第1章 引论
前言
这一章,阐述本书的目的,并简要复习离散数学以及程序设计的一些概念:
- 看到程序在较大输入情况下的运行性能与在适量输入情况下的运行性能具有同等重要性
- 总结本书其余部分所需要的数学基础
- 简要复习递归
1.1 本书讨论的内容
在许多问题当中,一个重要的观念是:写出一个可以工作的程序并不够。如果这个程序在巨大的数据集上运行,那么运行时间就变成了重要的问题。我们将在本书中看到对于大量的输入如何估计程序的运行时间,尤其是如何在尚未具体编码的情况下比较两个程序的运行时间。我们还将看到彻底改进程序速度以及确定程序瓶颈的方法。这些方法将使我们能够找到需要大力优化的那些代码段。
1.2 数学知识复习
本节列出一些需要记住或是能够推导出的基本公式,复习基本的证明方法
1.2.1 指数
1.2.2 对数
在计算机科学中,除非有特别的声明,所有的对数都是以2为底的
定义:当且仅当,
由该定义得到几个方便的等式:
定理1.1
;
定理1.2
其他有用的公式
(对所有的
成立)
,
,
,
1.2.3 级数
几何级数
收敛级数
算数级数
;
数叫作调和数,其和叫作调和和。以下近似式中的误差趋向于
,这个值称为欧拉常数(Euler's constant)
代数运算
1.2.4 模运算
如果N整除A-B,那么我们就说A与B模N同余(congruent),记为A=B(mod N)。直观地看,这意味着无论A还是B除以N,所得余数都是相同的。于是,81=61=1(mod 10)。如同等号的情形一样,若A=B(mod N),则A+C=B+C(mod N)以及AD=BD(mod N)。
有许多定理适用于模运算,其中有一些特别要用到数论来证明。我们将谨慎地使用模运算,这样,前面的一些定理也就足够了。
1.2.5 证明方法
1.3 递归简论
相关文章:
第1章 引论
前言 这一章,阐述本书的目的,并简要复习离散数学以及程序设计的一些概念: 看到程序在较大输入情况下的运行性能与在适量输入情况下的运行性能具有同等重要性总结本书其余部分所需要的数学基础简要复习递归 1.1 本书讨论的内容 在许多问题当中…...
)
深入探究Linux文件:.sh、.swp文件的作用与意义 (linux .sh.swp)
近年来,Linux操作系统已经成为了许多服务器、云计算平台、嵌入式设备等领域的首选。Linux操作系统囊括了大量的命令和文件,而其中 .sh 和 .swp 文件是许多 Linux 用户较为熟悉的两种文件类型。那么,这两种文件的作用和意义是什么呢࿱…...

优雅的使用String字符串处理各种类型转换
文章目录 🌟 优雅的使用String字符串处理各种类型转换🍊 基本类型转字符串🍊 字符串转基本类型🍊 字符串与字符数组的转换🍊 字符串与字节数组的转换🍊 其他类型转字符串🍊 总结 📕我…...

Harmony 个人中心(页面交互、跳转、导航、容器组件)
个人中心 前言正文一、创建工程二、登录① 更换启动页面② 拓展修饰符③ 页面跳转④ 等待进度条 三、导航栏四、首页① 轮播图② 网格列表 五、我的① 带参数跳转 六、源码 前言 今天是1024,祝各位程序员们,钱多事少离家近,不秃也强bug黄。在…...
AlDente Pro for Mac: 掌控电池充电的终极解决方案
你是否曾经为了保护你的MacBook的电池,而苦恼于无法控制它的充电速度?AlDente Pro for Mac 是一款专为Mac用户设计的电池管理工具,它能帮助你解决这个问题。 AlDente Pro for Mac 是一款电池最大充电限制软件,它能够让你自由地设…...
tomcat的负载均衡、动静分离(nginx联动)
动静分离: 访问静态页面和动态页面分开 实现动态和静态页面负载均衡 实验5台虚拟机 一、动态负载均衡 3台虚拟机模拟: 代理服务器:30 tomcat动态页面:21、22 代理服务器: proxy_pass http://tomcat; proxy_set_h…...

基于单片机的温湿度检测及远程控制系统设计
目 录 引 言. 2 第一章 绪 论. 2 1.1 单片机简介 2 1.2 传感器简介 2 1.3 LCD液晶显示器简介 2 1.4 本设计的主要内容和目标 2 第二章 系统总体设计. 2 2.1 系统功能要求与技术指标 2 2.1.1 功能要求. 2 2.1.2 技术指标. 2 2.2 系统设计思路 2 2.3系统设计原则 2 2.4 系…...
前后端交互系统:在Node.js中运行JavaScript
在Node.js中运行JavaScript,您需要编写适用于服务器端的代码,而不是浏览器端的代码。以下是一些示例代码,用于在Node.js中创建一个简单的HTTP服务器并在浏览器中访问它: // 引入Node.js内置的http模块 const http require(http);…...

Maven学习
Maven介绍 Maven是Apache的一个开源项目,主要服务于基于Java平台的项目构建,依赖管理和项目信息管理。 Maven可以让团队能够更科学的构建项目,我们可以用配置文件的方式,对项目的名称、描述、项目版本号、项目依赖等信息进行描述…...

《动手学深度学习 Pytorch版》 10.2 注意力汇聚:Nadaraya-Watson 核回归
import torch from torch import nn from d2l import torch as d2l1964 年提出的 Nadaraya-Watson 核回归模型是一个简单但完整的例子,可以用于演示具有注意力机制的机器学习。 10.2.1 生成数据集 根据下面的非线性函数生成一个人工数据集,其中噪声项 …...
测试C#调用Windows Media Player组件
新建基于.net framework的Winform项目,可以通过添加引用的方式选择COM组件中的Windows Media Player组件,如下图所示: 也可以在VS2022的工具箱空白处点右键,选择“选择项…”菜单。 在弹出的选择工具箱项窗口中…...

面试经典150题——Day20
文章目录 一、题目二、题解 一、题目 14. Longest Common Prefix Write a function to find the longest common prefix string amongst an array of strings. If there is no common prefix, return an empty string “”. Example 1: Input: strs [“flower”,“flow”…...
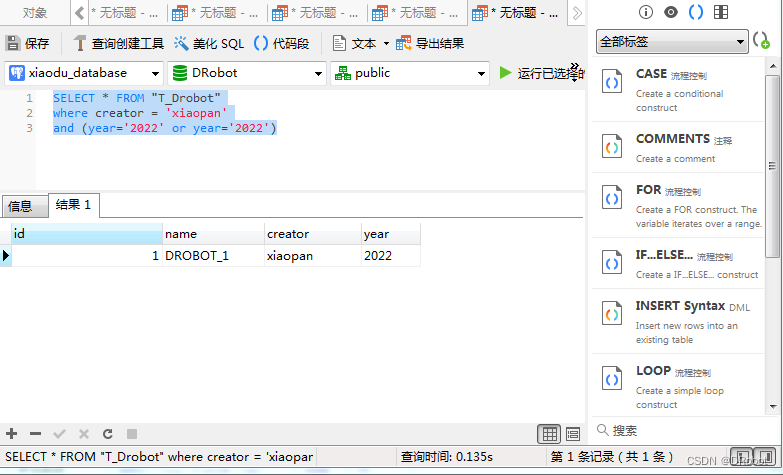
[SQL开发笔记]AND OR运算符复杂表达式开发实例
结合 AND & OR实例:通过圆括号使用and或or来组成复杂的表达式 目标数据库及表:使用 DRobot数据库,"T_Drobot" 表 假设我们需要查询"T_Drobot" 表,并从"T_Drobot"表中查询选取creator为 "…...

如何将本地 PDF 文件进行翻译
在日常工作和学习中,我们经常会遇到需要翻译 PDF 文件的情况。比如,我们需要将一份英文的技术文档翻译成中文,或者将一份中文的法律文件翻译成英文。 传统上,我们可以使用专业翻译软件或服务来翻译 PDF 文件。但是,这…...

Node.js的readline模块 命令行交互的模块
Node.js是一个非常流行的JavaScript运行时环境,它提供了许多内置模块来帮助我们开发应用程序。其中之一是readline模块,它提供了一种简单的方法来读取用户输入并进行交互。 本文将详细介绍readline模块的API和使用案例,并附有代码注释。 re…...

前沿重器[36] | ACL23-基于检索的大语言模型-报告阅读
前沿重器 栏目主要给大家分享各种大厂、顶会的论文和分享,从中抽取关键精华的部分和大家分享,和大家一起把握前沿技术。具体介绍:仓颉专项:飞机大炮我都会,利器心法我还有。(算起来,专项启动已经…...

2023秋招笔试算法Python3题解
诸神缄默不语-个人CSDN博文目录 签两方了,感觉秋招已经结束了,所以发布一下之前写的笔试编程题题解。 不全。可能有些题我会继续补。 不保证能过。 后续依然有可能继续刷算法题,但是就另外专门写博文来解析了。 打码是因为原则上其实是不让公…...
uniapp--点击上传图片到oss再保存数据给后端接口
项目采用uniapp与uview2.0组件库 --1.0的也可以参考一下,大差不差 一、项目要求与样式图 点击上传n张图片到oss,然后点击提交给后端 二、思路 1、打开上传按钮,弹出框内出现上传图片和提交按钮 2、点击上传图片区域,打开本地图…...
)
创建Secret(使用kubectl)
创建Secret(使用kubectl) 假设某个 Pod 需要访问数据库。在您执行 kubectl 命令所在机器的当前目录,创建文件 ./username.txt 文件和 ./password.txt 暂存数据库的用户名和密码,后续我们根据这两个文件配置 kubernetes secrets。…...

Notepad++正则查询替换操作
Notepad编辑器查找功能非常强大,本处记录一些实战中常用到复杂查询替换操作。 注意:如果是重要文件,替换操作前最好备份;当前一个操作后也可以用ctrlz恢复。 查找重复行 用查找(ctrlf)功能,用正则表达式模式匹配。 查…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
