C++笔记之初始化二维矩阵的方法
C++笔记之初始化二维矩阵的方法
—— 2023年5月20日 上海
code review!

文章目录
- C++笔记之初始化二维矩阵的方法
- 一.常见方法
- 1. 使用数组
- 2. 使用向量
- 3. 使用数组的动态分配
- 4. 使用嵌套的 std::vector 并使用resize方法
- 5. 初始化固定大小的 std::array
- 二.C++中使用vector初始化二维矩阵的所有方法
- 1. 列表初始化
- 2. 使用 `resize` 方法——重要:
- 3. 使用 `push_back` 方法:
- 4. 使用 `emplace_back` 方法:
- 5. 使用 `assign` 方法——重要:
- 6. 使用 `insert` 方法:
- 三.根据一个已有的二维矩阵使用std::vector来初始化一个新的二维矩阵
- 1. 使用拷贝构造函数——重要
- 2. 使用赋值运算符——重要
- 3. 使用 `assign` 方法
- 4. 使用 `std::copy` 函数
- 5. 使用 `std::copy_n` 函数
- 6. 使用范围基础的 for 循环和 `push_back` 方法
- 三.根据一个已有的二维矩阵使用std::vector来初始化一个新的同维度的,所有元素都为0的二维矩阵
- 1. 使用 `resize` 方法和循环——重要
- 2. 使用 `resize` 方法和 `std::transform` 函数
- 3. 使用嵌套的 `resize` 方法
一.常见方法
1. 使用数组
你可以使用二维数组来初始化一个矩阵:
int matrix[3][3] = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
2. 使用向量
你也可以使用std::vector来创建和初始化二维矩阵:
std::vector<std::vector<int>> matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
3. 使用数组的动态分配
如果你需要动态地创建矩阵(例如,其尺寸在运行时确定),可以使用new操作符:
int rows = 3;
int cols = 3;
int** matrix = new int*[rows];
for(int i = 0; i < rows; ++i)matrix[i] = new int[cols];
然后你可以使用循环来初始化这个矩阵。
4. 使用嵌套的 std::vector 并使用resize方法
如果你需要动态地创建和初始化矩阵,但你更喜欢使用std::vector,你可以这样做:
int rows = 3;
int cols = 3;
std::vector<std::vector<int>> matrix;
matrix.resize(rows, std::vector<int>(cols, 0)); // 这将创建一个3x3的矩阵,并用0填充
5. 初始化固定大小的 std::array
对于固定大小的二维矩阵,可以使用std::array:
std::array<std::array<int, 3>, 3> matrix = { { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} } };

二.C++中使用vector初始化二维矩阵的所有方法
在 C++ 中,使用 std::vector 来初始化二维矩阵是常见的做法,因为它提供了灵活的大小和方便的内存管理。以下是一些方法:
1. 列表初始化
你可以在声明时就初始化 std::vector:
std::vector<std::vector<int>> matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
2. 使用 resize 方法——重要:
如果你已经知道矩阵的大小,但要稍后填充值,可以使用 resize 方法:
std::vector<std::vector<int>> matrix;
matrix.resize(rows, std::vector<int>(cols));
3. 使用 push_back 方法:
你也可以创建一个空的 std::vector,然后使用 push_back 方法来添加行:
std::vector<std::vector<int>> matrix;
for(int i = 0; i < rows; ++i) {std::vector<int> row;for(int j = 0; j < cols; ++j) {row.push_back(value);}matrix.push_back(row);
}
4. 使用 emplace_back 方法:
类似于 push_back,但 emplace_back 直接在原地构造新元素,通常效率更高:
std::vector<std::vector<int>> matrix;
for(int i = 0; i < rows; ++i) {matrix.emplace_back(std::vector<int>(cols, value));
}
5. 使用 assign 方法——重要:
assign 方法可以用来替换 std::vector 中的所有元素:
std::vector<std::vector<int>> matrix;
matrix.assign(rows, std::vector<int>(cols, value));
6. 使用 insert 方法:
insert 方法可以在 std::vector 的任何位置插入新元素:
std::vector<std::vector<int>> matrix;
for(int i = 0; i < rows; ++i) {matrix.insert(matrix.end(), std::vector<int>(cols, value));
}
注意,在这些例子中,rows、cols 和 value 都是整数变量,分别表示矩阵的行数、列数和初始值。
三.根据一个已有的二维矩阵使用std::vector来初始化一个新的二维矩阵
在C++中,如果你已经有一个二维矩阵,你可以通过多种方式使用std::vector来初始化一个新的二维矩阵:
1. 使用拷贝构造函数——重要
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix(old_matrix);
2. 使用赋值运算符——重要
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix = old_matrix;
3. 使用 assign 方法
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix;
new_matrix.assign(old_matrix.begin(), old_matrix.end());
4. 使用 std::copy 函数
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix(old_matrix.size());
std::copy(old_matrix.begin(), old_matrix.end(), new_matrix.begin());
5. 使用 std::copy_n 函数
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix(old_matrix.size());
std::copy_n(old_matrix.begin(), old_matrix.size(), new_matrix.begin());
6. 使用范围基础的 for 循环和 push_back 方法
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix;
for (const auto &row : old_matrix) {new_matrix.push_back(row);
}
以上就是使用 std::vector 根据已有的二维矩阵初始化新的二维矩阵的一些方法。根据你的具体需求和优化考虑,你可能需要选择不同的方法。
三.根据一个已有的二维矩阵使用std::vector来初始化一个新的同维度的,所有元素都为0的二维矩阵
在C++中,如果你已经有一个二维矩阵,并希望创建一个新的、同维度的、所有元素都为0的二维矩阵,以下是一些方法:
1. 使用 resize 方法和循环——重要
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix;
for(const auto &row : old_matrix) {new_matrix.push_back(std::vector<int>(row.size(), 0));
}
2. 使用 resize 方法和 std::transform 函数
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix(old_matrix.size());
std::transform(old_matrix.begin(), old_matrix.end(), new_matrix.begin(), [](const std::vector<int>& row) {return std::vector<int>(row.size(), 0);
});
3. 使用嵌套的 resize 方法
std::vector<std::vector<int>> old_matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} };
std::vector<std::vector<int>> new_matrix;
new_matrix.resize(old_matrix.size());
for(size_t i = 0; i < old_matrix.size(); ++i) {new_matrix[i].resize(old_matrix[i].size(), 0);
}
在以上的所有例子中,old_matrix 是你已有的二维矩阵,new_matrix 是新创建的二维矩阵。所有的新矩阵元素都被初始化为0,并且新矩阵的尺寸与原矩阵相同。
相关文章:

C++笔记之初始化二维矩阵的方法
C笔记之初始化二维矩阵的方法 —— 2023年5月20日 上海 code review! 文章目录 C笔记之初始化二维矩阵的方法一.常见方法1. 使用数组2. 使用向量3. 使用数组的动态分配4. 使用嵌套的 std::vector 并使用resize方法5. 初始化固定大小的 std::array 二.C中使用vector初始化二维矩…...
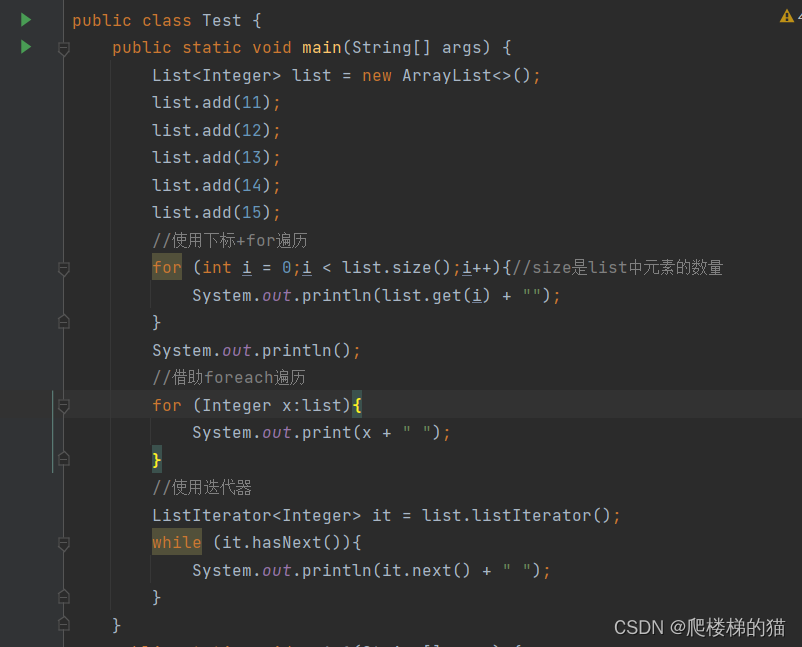
ArrayList与List的层级关系及ArrayList解析
List与ArrayList的关系 List List是一个接口,不能直接实例化。如果要使用必须去实例化List的实现类——ArrayList和LinkedList站在数据结构的角度看,List就是一个线性表。常见的线性表:顺序表、链表、栈、队列等 线性表 线性表是n个具有相…...

智慧公厕设备选型攻略,打造智能化便利生活体验
智慧公厕设备的选型对于打造智能化便利生活体验起着至关重要的作用。在不断提升城市品质的背景下,智慧公厕已成为城市建设中的一项重要内容。在选购智慧公厕设备时,我们需要考虑到不同版本的功能要求,确保公厕设备的质量和性能。本文以智慧公…...
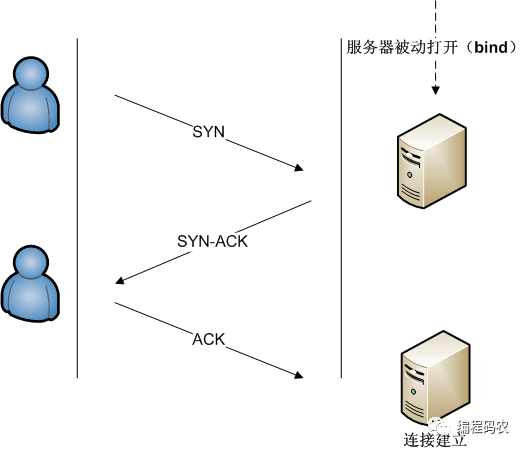
TCP 协议的可靠传输机制是怎样实现的?
TCP 协议是一种面向连接的、可靠的、基于字节流的传输层协议。 1 它通过以下几种方法来保证数据传输的可靠性: 检验和:TCP 在发送和接收数据时,都会计算一个检验和,用来检测数据是否在传输过程中发生了错误或损坏。如果检验和不匹…...
Antv G6入门之旅--combo图
目录 什么是AntV G6 G6 的特性 G6 文档 安装 1 在项目中使用 NPM 包引入 2 在 HTML 中使用 CDN 引入 使用 Step 1 创建容器 Step 2 数据准备 Step 3 创建关系图 Step 4 配置数据源,渲染 React 中使用 G6 Combo图 什么是AntV G6 G6 是一个图可视化引擎…...
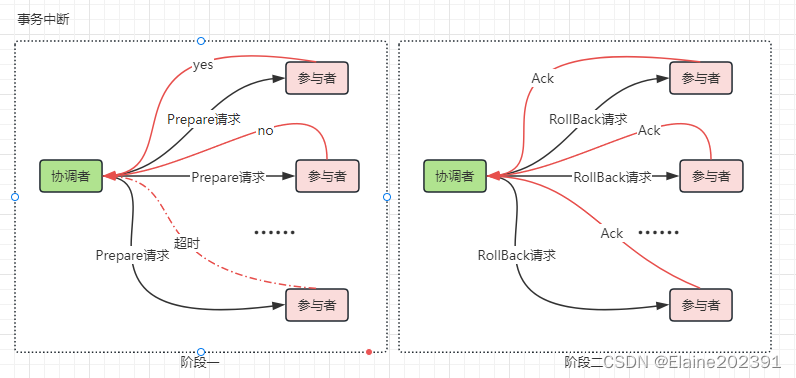
聊聊分布式架构09——分布式中的一致性协议
目录 01从集中式到分布式 系统特点 集中式特点 分布式特点 事务处理差异 02一致性协议与Paxos算法 2PC(Two-Phase Commit) 阶段一:提交事务请求 阶段二:执行事务提交 优缺点 3PC(Three-Phase Commit&#x…...

探索流视频的发送
1.网络连接 2.主设备将某处视频开始的视频数据发送给从设备。 之前有读取本地视频并播放的demo,所以可以先测试网络连接的问题。 先用模拟器进行模拟吧。方便进行测试。 是的,可以使用Android设备使用上述库或框架来构建实时Web应用程序。虽然这些库和框架在Java服…...
[ACTF2020 新生赛]Include 1
题目环境:超链接,点进去看看你能找到flag吗?除了这些网页什么都没有,但是不当紧,因为我们有一双善于发现的眼睛👀F12瞅瞅无,并无其他等等URL看了吗?发现存在一个参数file,…...

教师必备宝藏,强烈推荐
亲爱的教师朋友们,你们是不是在为学期末成绩查询而头疼呢?一学期下来,成堆的试卷和成绩单,还有学生家长的各种咨询,让人应接不暇。现在,我给你们分享一个教师必备的宝藏,让你们的成绩查询工作变…...

「北大社送书」学习MATLAB—从算法到实战
MATLAB科学计算从入门到精通 一句话推荐书籍特色内容简介书籍概览 从代码到函数,从算法到实战,从问题到应用,由浅入深掌握科学计算方法,高效解决实际问题。 一句话推荐 科学计算基础入门,高效解决实际问题。 书籍特色…...

clion安装C++远程linux开发并调试 从装centos虚拟机到完美开发调试
下载镜像 阿里云镜像 从vmware上安装虚拟机并提权开放ssh 更新编译环境 一般 gcc gdb 版本都是比较低的,适配不了clion的最低要求。 升级gdb参考博客 升级gcc参考博客 安装CMAKE 官方的源使用wget即可下载 未找到openssl的解决办法 注意版本,又踩个…...

Android笔记
目录 触摸事件java弱引用WorkerThread注解NonNull注解camera.setFrameProcessingFormat(ImageFormat.YUV_420_888);YUV_420_888的字节数据长啥样YUV_420_888的字节数组长啥样 触摸事件 java弱引用 创建对象的弱引用,在没有强引用指向改对象的情况下,垃圾…...

Java虚拟机内存区域、异常、垃圾收集器
java虚拟机 java内存区域 jvm的主要组成部分及作用 主要包含两个子系统和两个组件 子系统 类加载器(Class loader):根据给定的类路径来装载class文件到运行时数据区 …...

深入理解JVM虚拟机第十三篇:详解JVM中的程序计数器
文章目录 一:程序计数器 1:概念 2:官方说法 3:图解 4:特点...
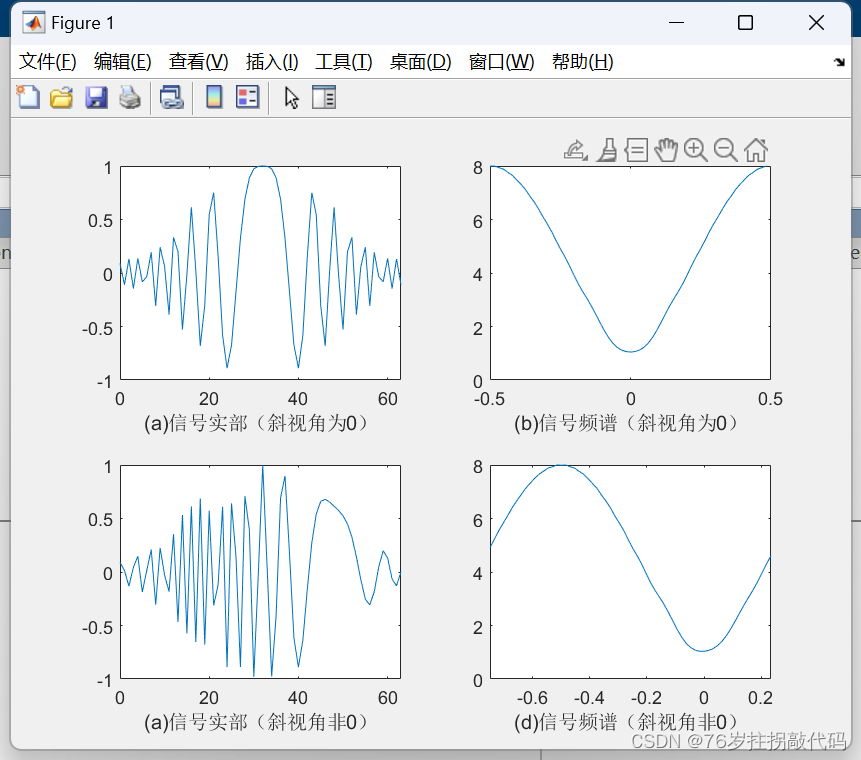
《合成孔径雷达成像算法与实现》Figure5.5
clc clear close all%% 参数设置 Ta 64; % 脉冲持续时间 Ka -1.56e-2; % 方位向调频率 Delta_f_dop abs(Ta*Ka); …...

leetcode经典面试150题---2.移除元素
题目描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新…...

【尘缘赠书活动:01期】Python数据挖掘——入门进阶与实用案例分析
引言 本案例将根据已收集到的电力数据,深度挖掘各电力设备的电流、电压和功率等情况,分析各电力设备的实际用电量,进而为电力公司制定电能能源策略提供一定的参考依据。更多详细内容请参考**《Python数据挖掘:入门进阶与实用案例…...

计算机网络(谢希仁)第八版课后题答案(第二章)
1.物理层要解决哪些问题?物理层的主要特点是什么? (1)物理层要尽可能地屏蔽掉物理设备和传输媒体,通信手段的不同,使数据链路层感觉不到这些差异,只考虑完成本层的协议和服务。 (2)给其服务用户(数据链路…...

搭建nuxt3项目(框架构建)
需求 目标:我想搭建一个nuxt3的框架,实现一些基本的组件和路由、页面,方便后续遇到相关ssr项目直接复用。 同时:记录关于nuxt3的使用介绍关于Nuxt(详解以及周边) Nuxt 框架 1、一种基于 Node.js 的服务端…...

系统架构设计之微内核架构(Microkernel Architecture)
微内核架构(Microkernel Architecture) 一. 什么是微内核架构二. 微内核架构风格-拓扑结构三. 微内核的核心系统设计的三个关键点3.1 插件管理3.2 插件连接3.3 插件通信 四. 微内核架构的优缺点 一. 什么是微内核架构 微内核架构是一种面向功能进行拆分的…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
