线性代数-Python-03:矩阵的变换 - 手写Matrix Transformation及numpy中的用法
文章目录
- 一、代码仓库
- 二、旋转矩阵的推导及图形学中的矩阵变换
- 2.1 让横坐标扩大a倍,纵坐标扩大b倍
- 2.2 关于x轴翻转
- 2.3 关于y轴翻转
- 2.4 关于原点翻转(x轴,y轴均翻转)
- 2.5 沿x方向错切
- 2.6 沿y方向错切
- 2.7 旋转
- 2.8 单位矩阵
- 2.9 矩阵的逆
- 三、看待矩阵的关键视角:用矩阵表示空间
- 3.1 行视角
- 3.2 列视角
- 3.3 标准单位向量和列视角
- 3.4 矩阵表示空间
- 四、代码
- matrix.py
- matrix_transformation
- numpy_matrix.py
一、代码仓库
https://github.com/Chufeng-Jiang/Python-Linear-Algebra-for-Beginner/tree/main
二、旋转矩阵的推导及图形学中的矩阵变换
2.1 让横坐标扩大a倍,纵坐标扩大b倍
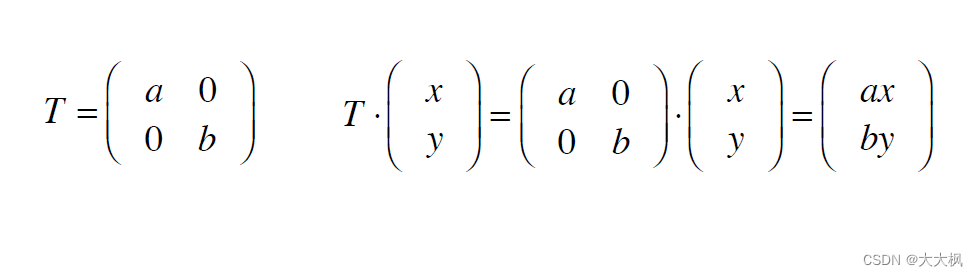
2.2 关于x轴翻转
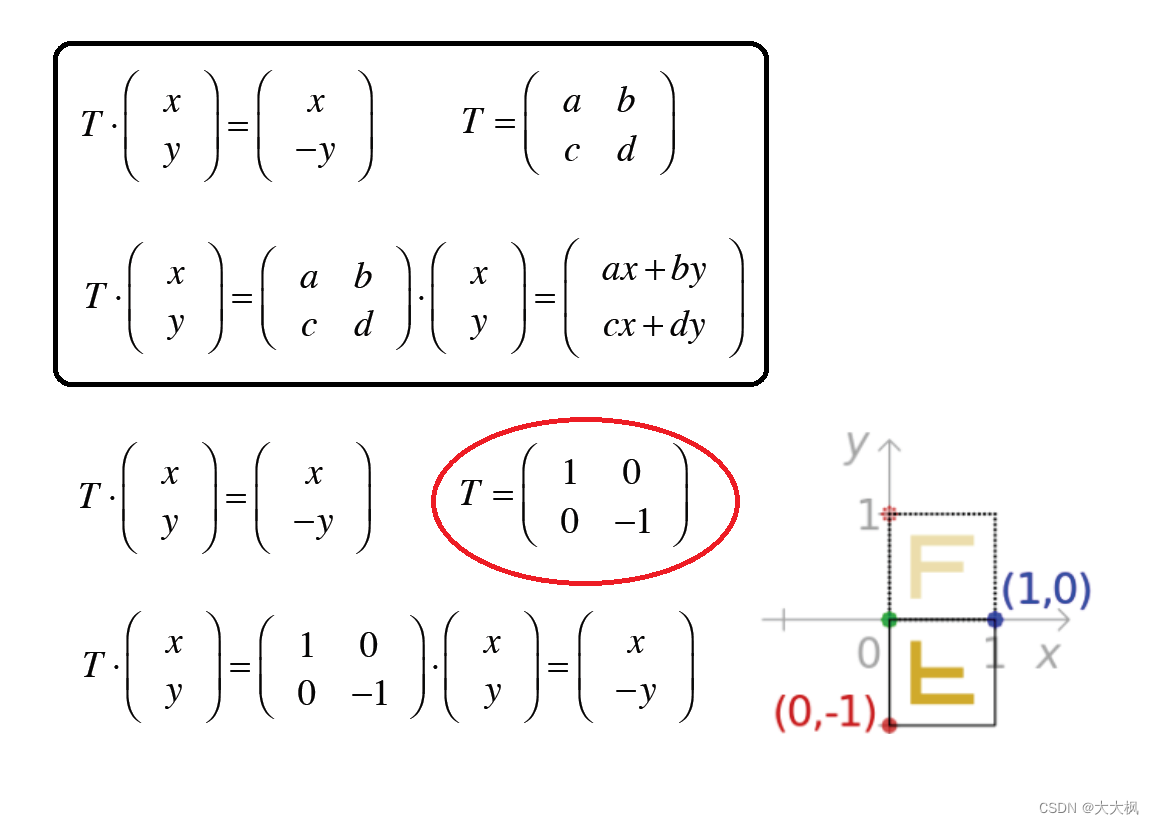
2.3 关于y轴翻转
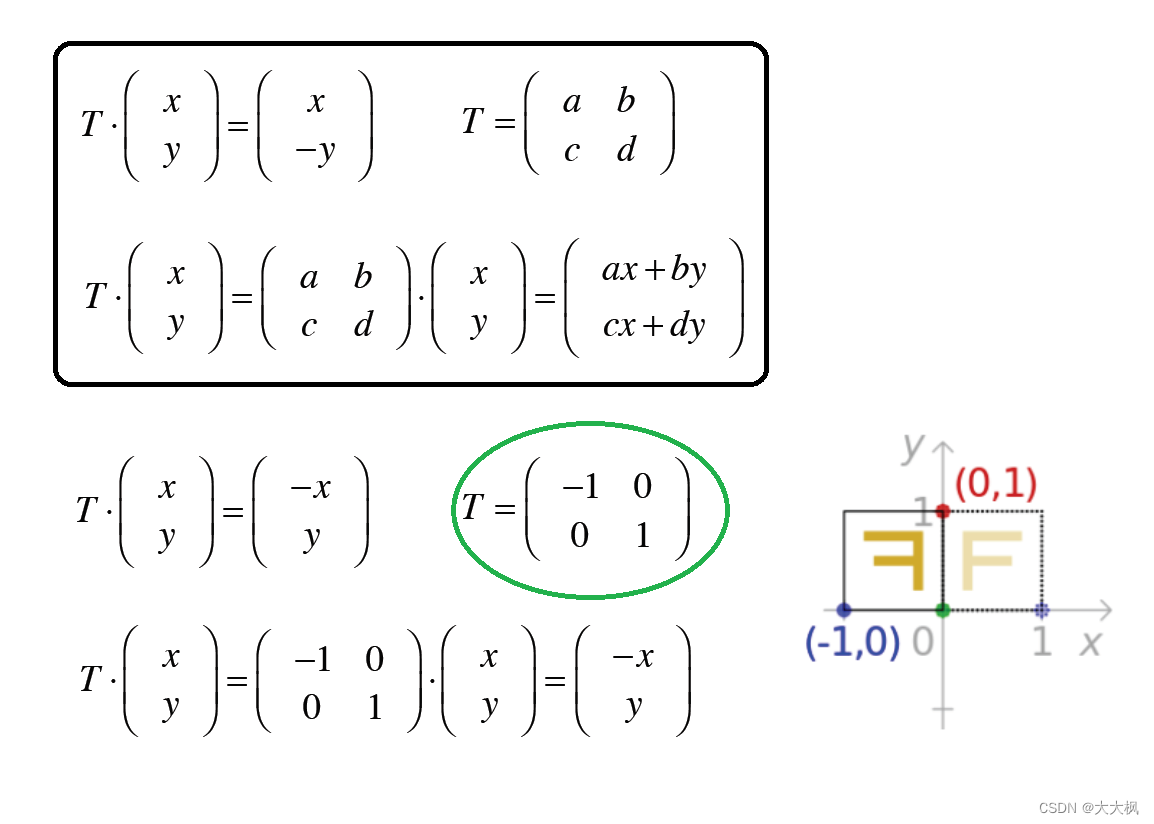
2.4 关于原点翻转(x轴,y轴均翻转)
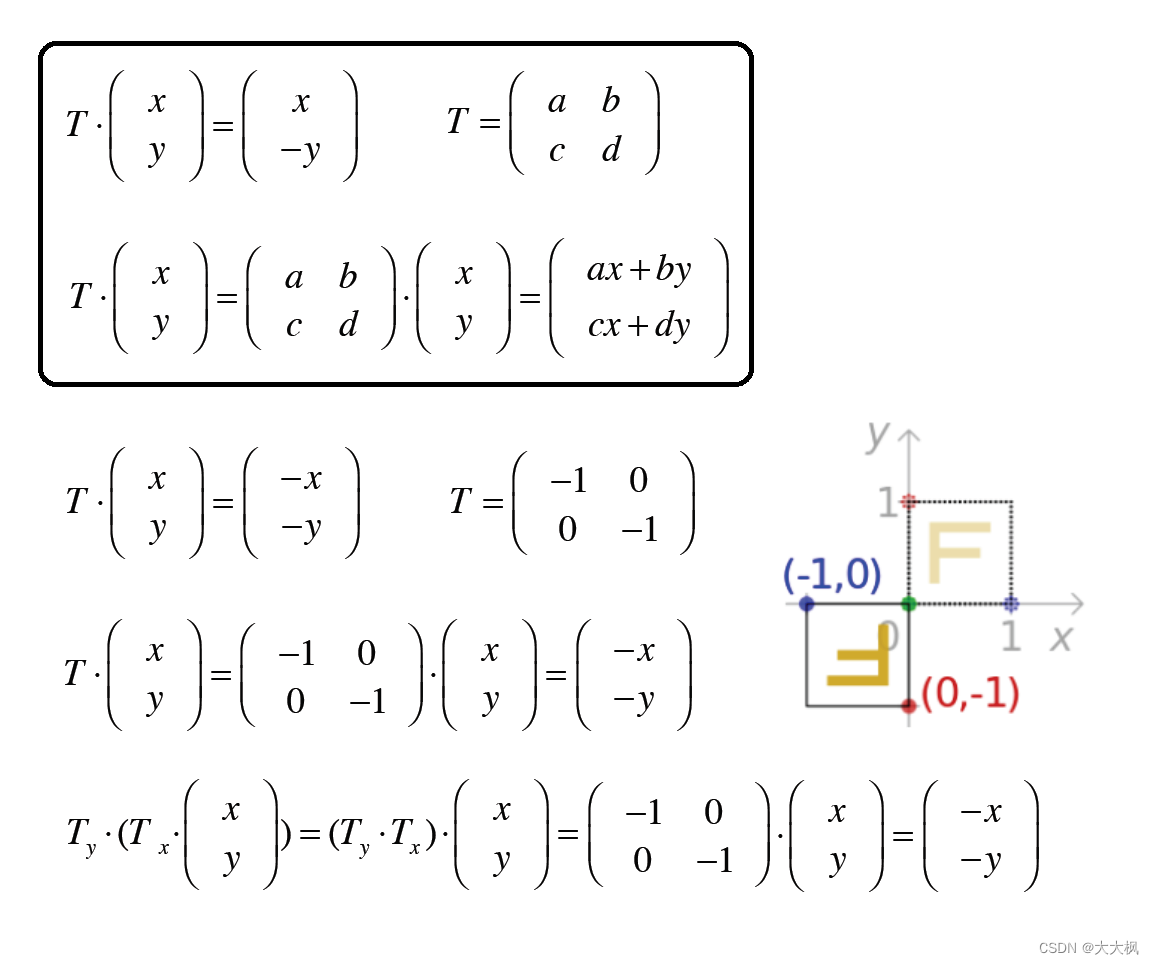
2.5 沿x方向错切

2.6 沿y方向错切
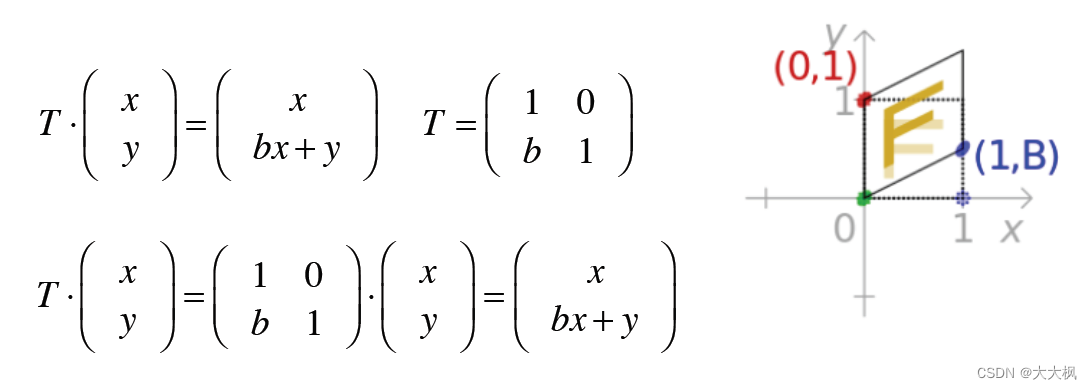
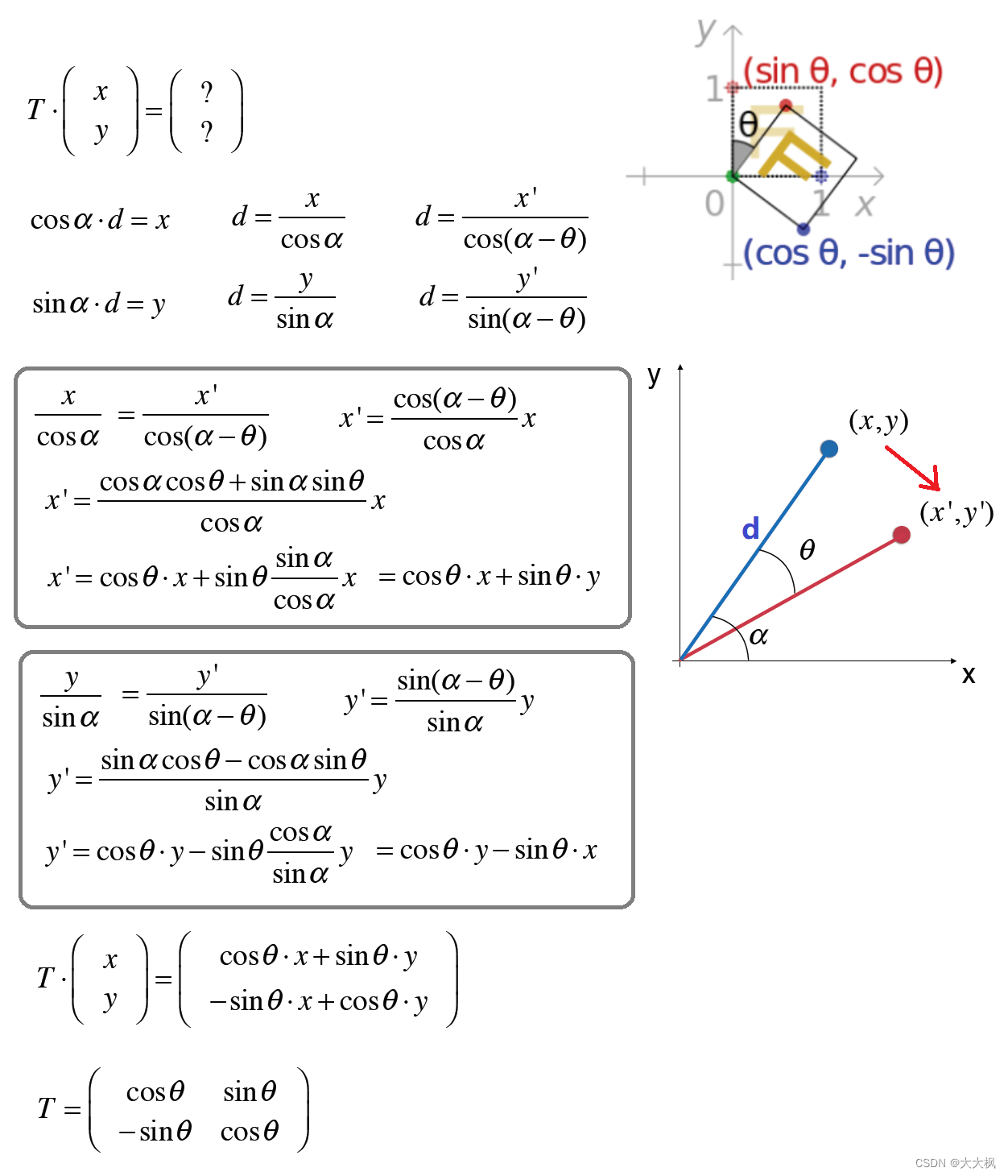
2.7 旋转
theta = math.pi / 3
T = Matrix([[math.cos(theta), math.sin(theta)], [-math.sin(theta), math.cos(theta)]])
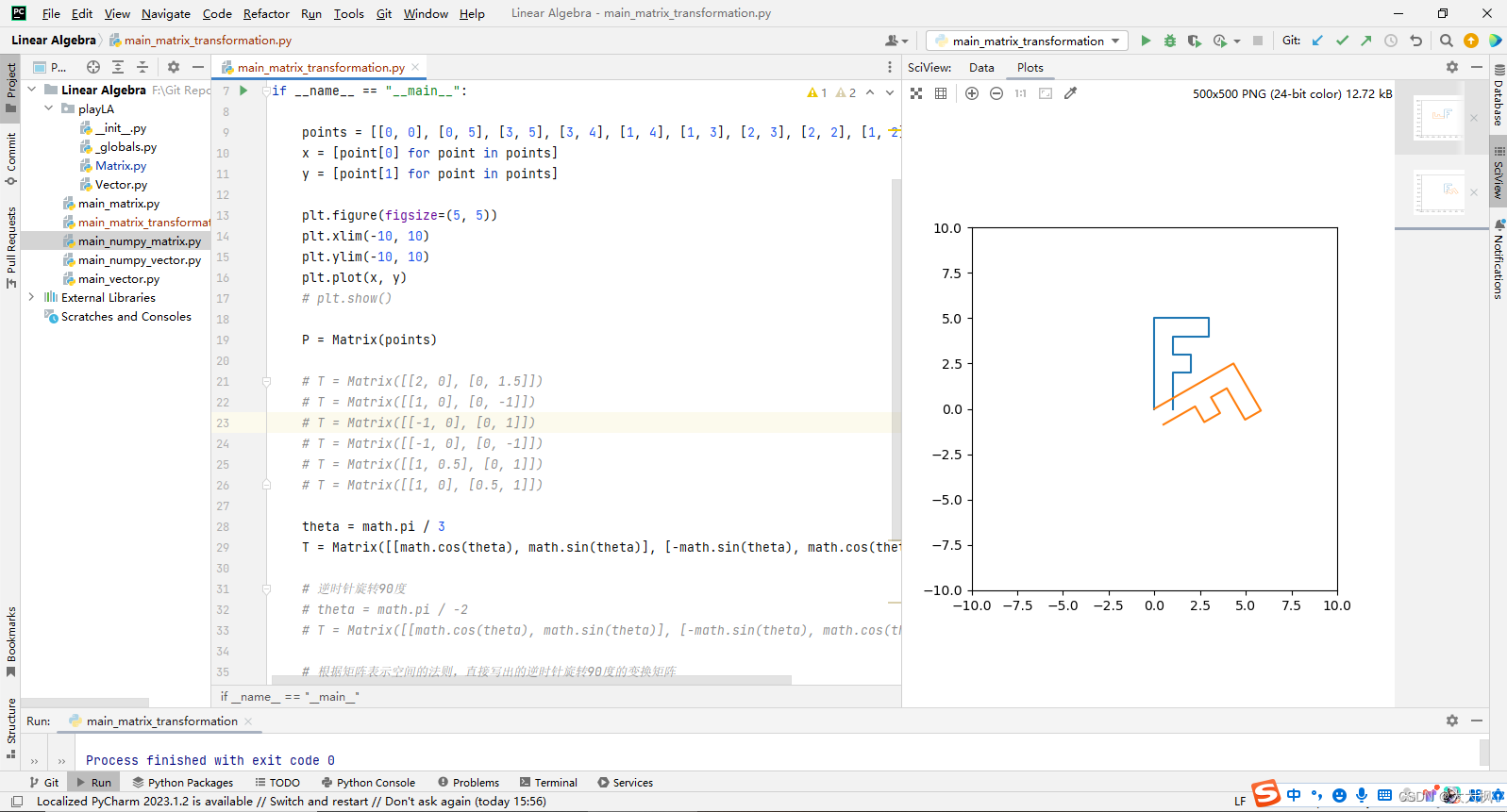
2.8 单位矩阵

2.9 矩阵的逆

三、看待矩阵的关键视角:用矩阵表示空间
3.1 行视角
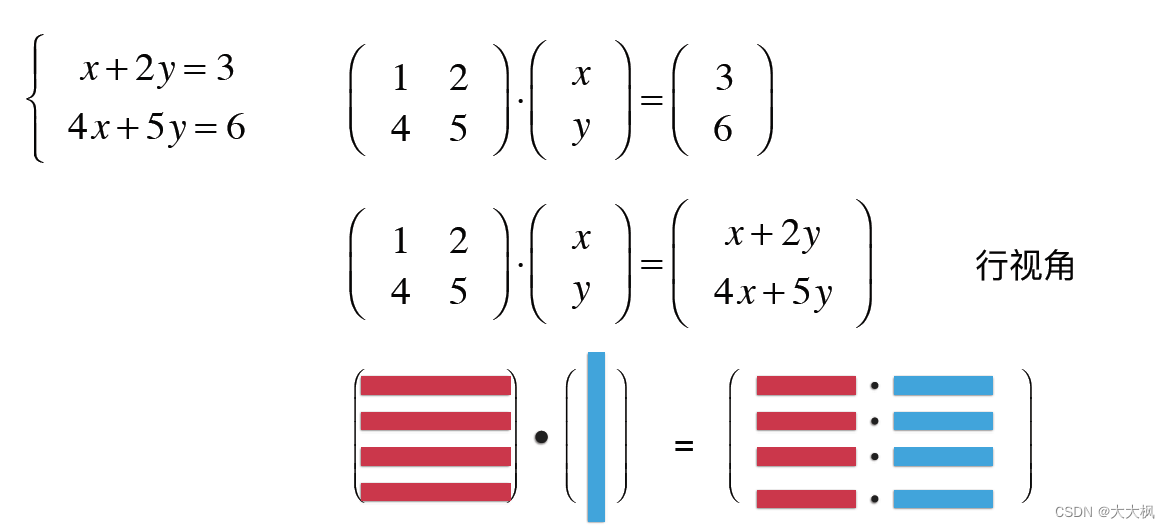
3.2 列视角
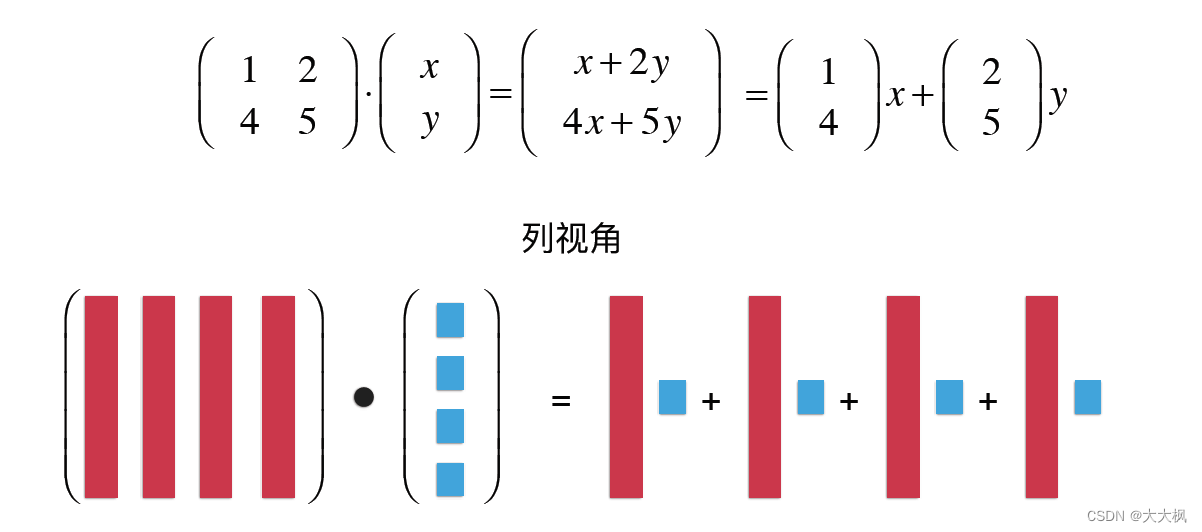
3.3 标准单位向量和列视角
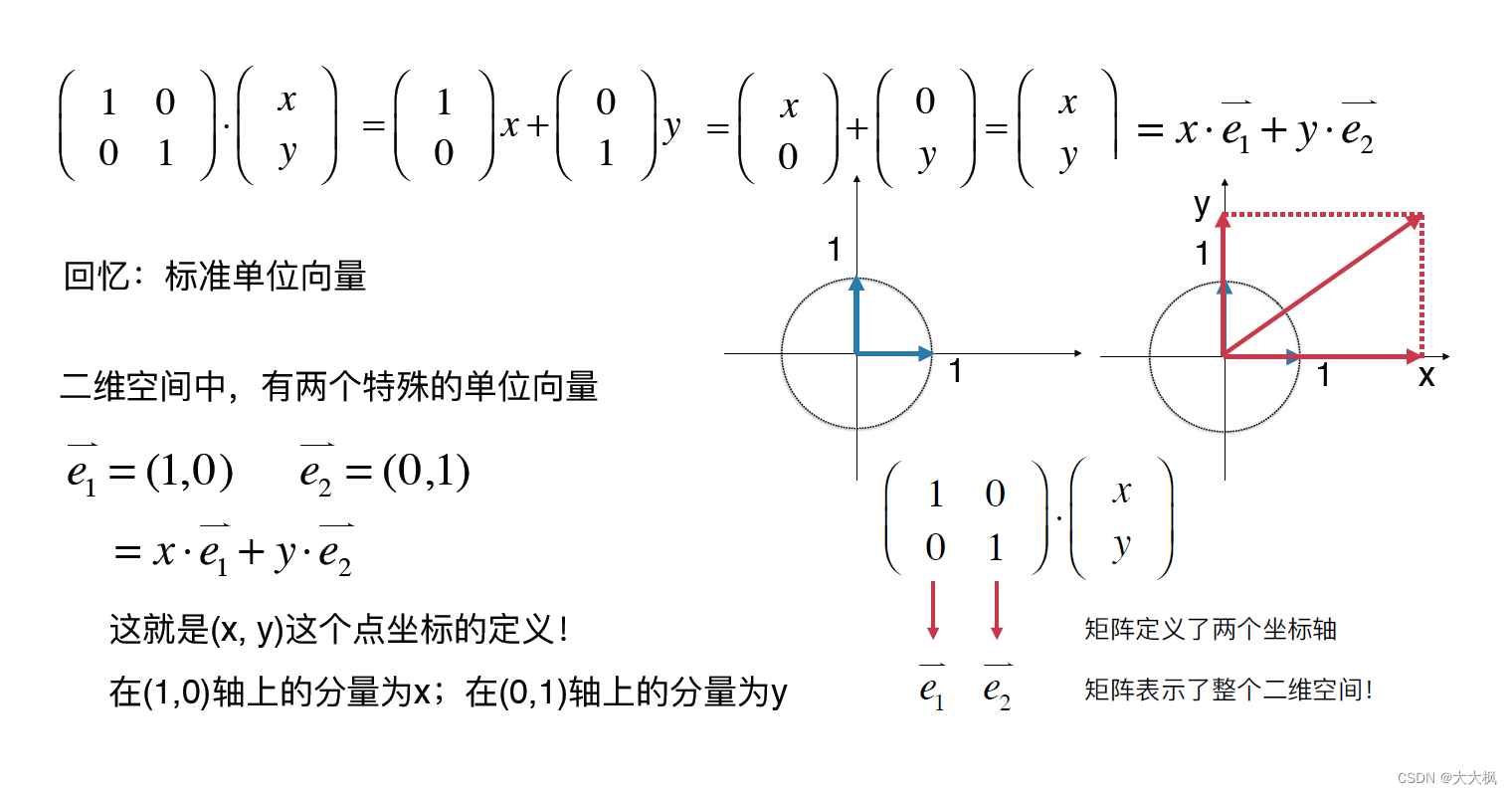
3.4 矩阵表示空间
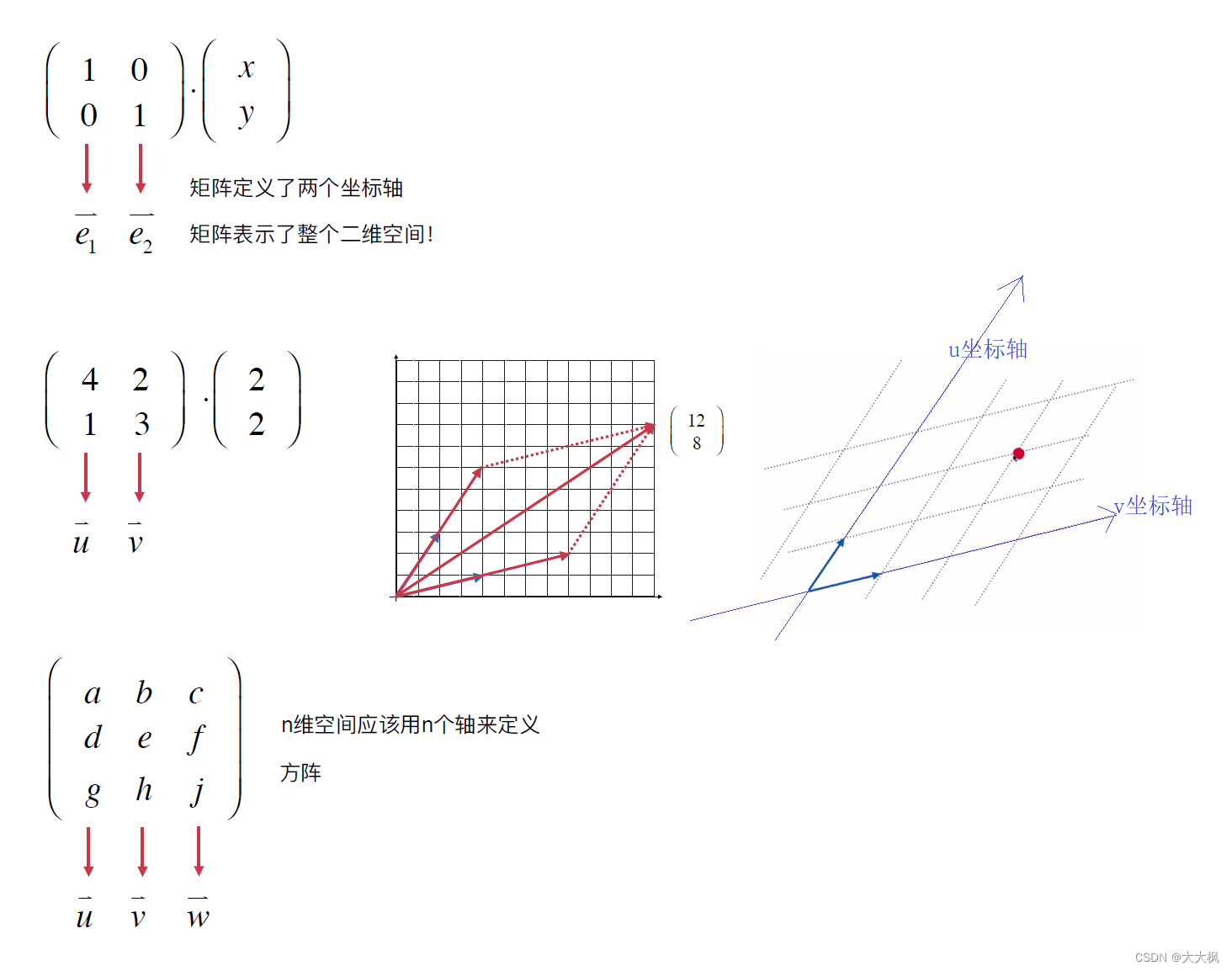
四、代码
matrix.py
from .Vector import Vectorclass Matrix:def __init__(self, list2d):self._values = [row[:] for row in list2d]@classmethoddef zero(cls, r, c):"""返回一个r行c列的零矩阵"""return cls([[0] * c for _ in range(r)])@classmethoddef identity(cls, n):"""返回一个n行n列的单位矩阵"""m = [[0]*n for _ in range(n)]for i in range(n):m[i][i] = 1;return cls(m)def T(self):"""返回矩阵的转置矩阵"""return Matrix([[e for e in self.col_vector(i)]for i in range(self.col_num())])def __add__(self, another):"""返回两个矩阵的加法结果"""assert self.shape() == another.shape(), \"Error in adding. Shape of matrix must be same."return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __sub__(self, another):"""返回两个矩阵的减法结果"""assert self.shape() == another.shape(), \"Error in subtracting. Shape of matrix must be same."return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def dot(self, another):"""返回矩阵乘法的结果"""if isinstance(another, Vector):# 矩阵和向量的乘法assert self.col_num() == len(another), \"Error in Matrix-Vector Multiplication."return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])if isinstance(another, Matrix):# 矩阵和矩阵的乘法assert self.col_num() == another.row_num(), \"Error in Matrix-Matrix Multiplication."return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())]for i in range(self.row_num())])def __mul__(self, k):"""返回矩阵的数量乘结果: self * k"""return Matrix([[e * k for e in self.row_vector(i)]for i in range(self.row_num())])def __rmul__(self, k):"""返回矩阵的数量乘结果: k * self"""return self * kdef __truediv__(self, k):"""返回数量除法的结果矩阵:self / k"""return (1 / k) * selfdef __pos__(self):"""返回矩阵取正的结果"""return 1 * selfdef __neg__(self):"""返回矩阵取负的结果"""return -1 * selfdef row_vector(self, index):"""返回矩阵的第index个行向量"""return Vector(self._values[index])def col_vector(self, index):"""返回矩阵的第index个列向量"""return Vector([row[index] for row in self._values])def __getitem__(self, pos):"""返回矩阵pos位置的元素"""r, c = posreturn self._values[r][c]def size(self):"""返回矩阵的元素个数"""r, c = self.shape()return r * cdef row_num(self):"""返回矩阵的行数"""return self.shape()[0]__len__ = row_numdef col_num(self):"""返回矩阵的列数"""return self.shape()[1]def shape(self):"""返回矩阵的形状: (行数, 列数)"""return len(self._values), len(self._values[0])def __repr__(self):return "Matrix({})".format(self._values)__str__ = __repr__matrix_transformation
import matplotlib.pyplot as plt
from playLA.Matrix import Matrix
from playLA.Vector import Vector
import mathif __name__ == "__main__":points = [[0, 0], [0, 5], [3, 5], [3, 4], [1, 4], [1, 3], [2, 3], [2, 2], [1, 2], [1, 0]]x = [point[0] for point in points]y = [point[1] for point in points]plt.figure(figsize=(5, 5))plt.xlim(-10, 10)plt.ylim(-10, 10)plt.plot(x, y)# plt.show()P = Matrix(points)# T = Matrix([[2, 0], [0, 1.5]])# T = Matrix([[1, 0], [0, -1]])# T = Matrix([[-1, 0], [0, 1]])# T = Matrix([[-1, 0], [0, -1]])# T = Matrix([[1, 0.5], [0, 1]])# T = Matrix([[1, 0], [0.5, 1]])theta = math.pi / 3T = Matrix([[math.cos(theta), math.sin(theta)], [-math.sin(theta), math.cos(theta)]])# 逆时针旋转90度# theta = math.pi / -2# T = Matrix([[math.cos(theta), math.sin(theta)], [-math.sin(theta), math.cos(theta)]])# 根据矩阵表示空间的法则,直接写出的逆时针旋转90度的变换矩阵#T = Matrix([[0, -1], [1, 0]])P2 = T.dot(P.T())plt.plot([P2.col_vector(i)[0] for i in range(P2.col_num())],[P2.col_vector(i)[1] for i in range(P2.col_num())])plt.show()
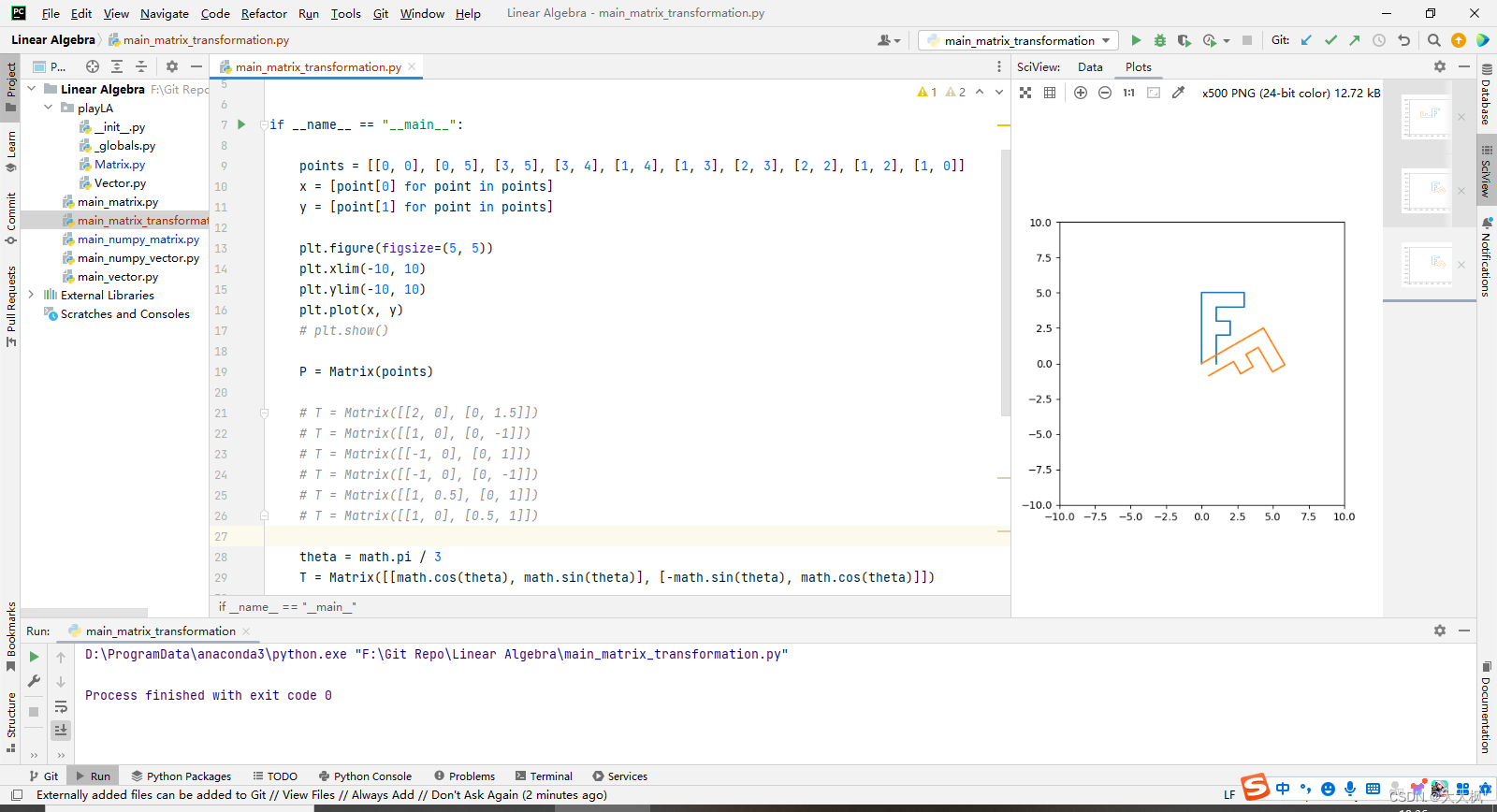
numpy_matrix.py
import numpy as npif __name__ == "__main__":# 矩阵的创建A = np.array([[1, 2], [3, 4]])print(A)# 矩阵的属性print(A.shape)print(A.T)# 获取矩阵的元素print(A[1, 1])print(A[0])print(A[:, 0])print(A[1, :])# 矩阵的基本运算B = np.array([[5, 6], [7, 8]])print(A + B)print(A - B)print(10 * A)print(A * 10)print(A * B)print(A.dot(B))p = np.array([10, 100])print(A + p)print(A + 1)print(A.dot(p))# 单位矩阵I = np.identity(2)print(I)print(A.dot(I))print(I.dot(A))# 逆矩阵invA = np.linalg.inv(A)print(invA)print(invA.dot(A))print(A.dot(invA))# C = np.array([[1, 2, 3], [4, 5, 6]])# np.linalg.inv(C)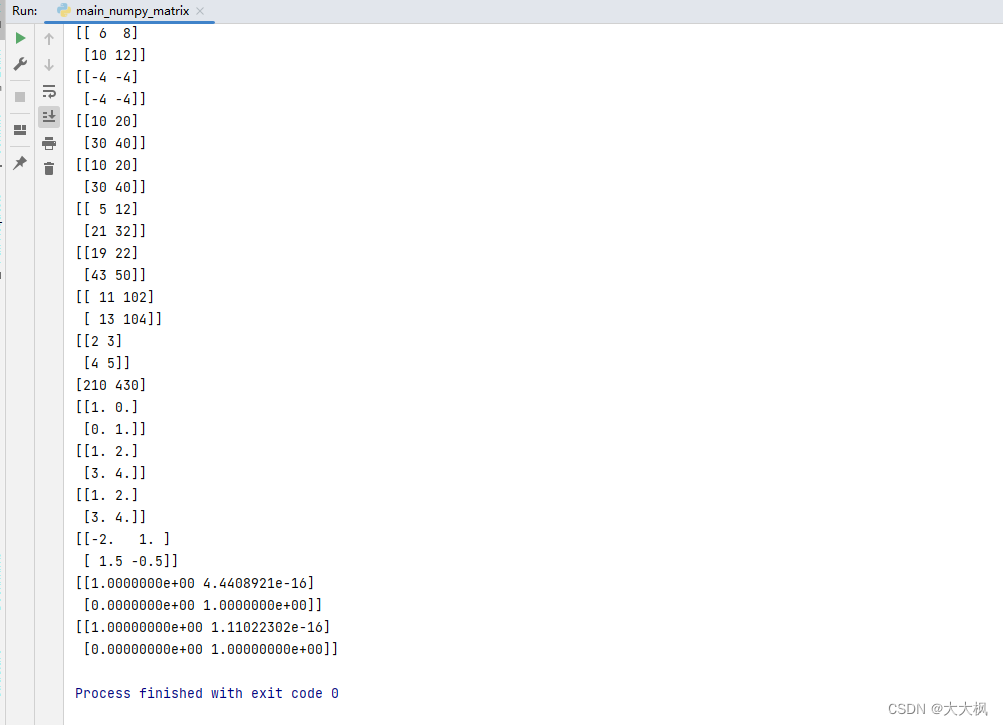
相关文章:

线性代数-Python-03:矩阵的变换 - 手写Matrix Transformation及numpy中的用法
文章目录 一、代码仓库二、旋转矩阵的推导及图形学中的矩阵变换2.1 让横坐标扩大a倍,纵坐标扩大b倍2.2 关于x轴翻转2.3 关于y轴翻转2.4 关于原点翻转(x轴,y轴均翻转)2.5 沿x方向错切2.6 沿y方向错切2.7 旋转2.8 单位矩阵2.9 矩阵的…...

【单片机基础】按键状态机实现短按、长按、双击、三击和N击
下载地址: 【CSDNNaiva】源码:HK32F030M-按键扫描-短按长按检测【CSDNNaiva】源码:HK32F030M-ADC-EXTI-TM1624-USART-EEPROM-TiMBase-按键长按(231024) 参考资料 [1] 【CSDNPillarPeng】【按键】[独立按键] - 1: 单击,…...
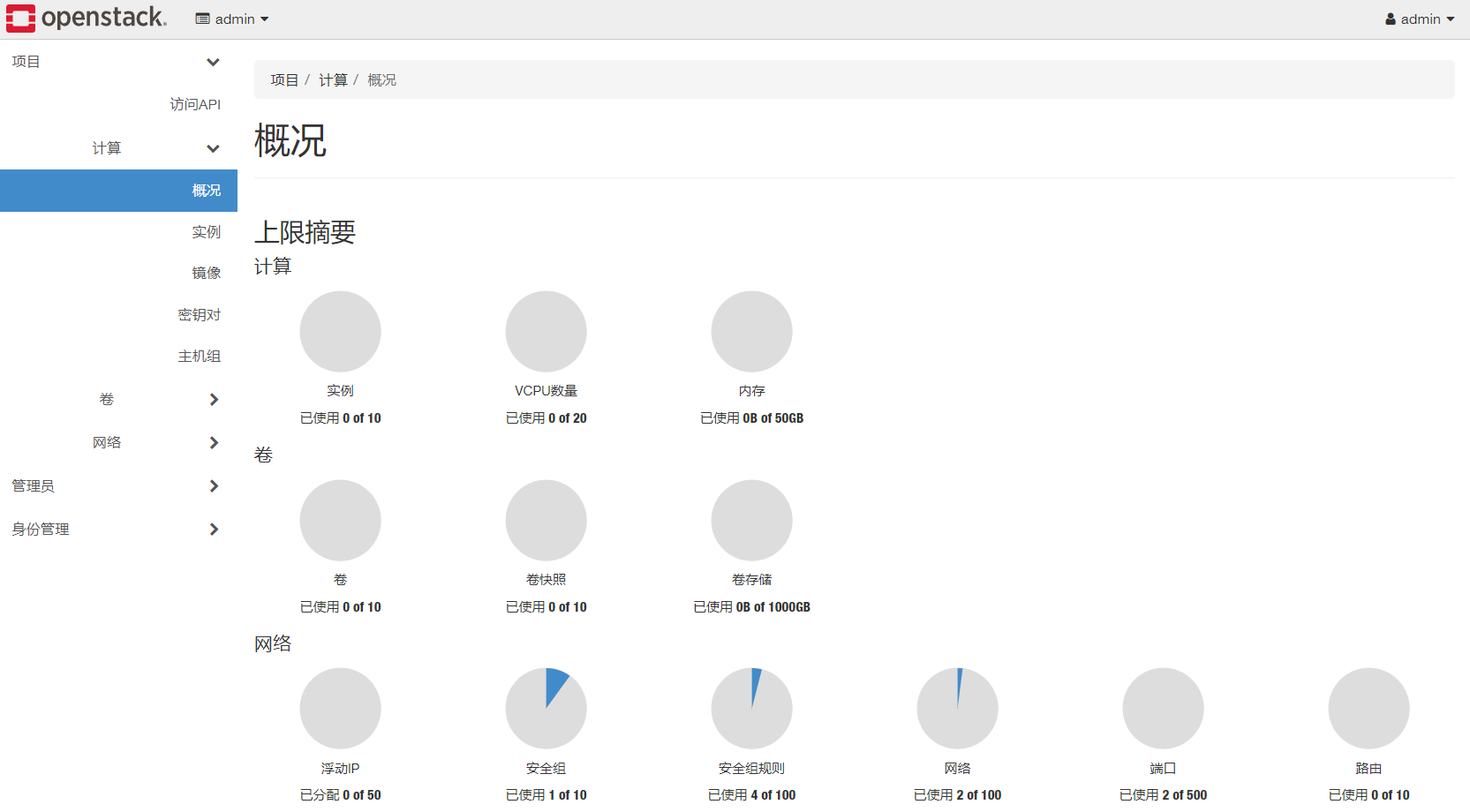
Ubuntu虚拟机部署OpenStack
1、部署环境 系统:ubuntu-22.04.3-desktop-amd64DevStack版本:2024.1VMware Workstation:8G内存、4核处理器、100G硬盘/1、网络NAT模式/1 2、Ubuntu环境设置 点击show applications,选择Software&Updates 跟换Ubuntu的镜像…...

ES在企业项目中的实战总结,彻底掌握ES的使用
通过之前两篇文章 了解了ES的核心概念和基础使用学习进阶的DSL语法处理复杂的查询 这段时间通过在本企业代码中对ES框架的使用,总结了不少经验。主要分为三点 企业封装了ES原生的api,需要使用企业项目提供的接口实现 -------简单使用(本章节目…...
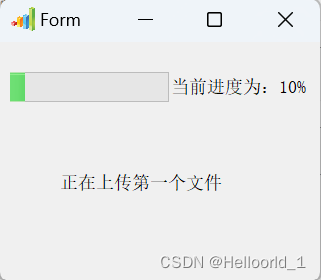
QT的Qporcess功能的使用
具体实现代码如下: #include <QProgressBar>//必须要包含的头文件 #include <QProcess>// 创建一个QProgressBar对象QProgressBar *progressBar new QProgressBar(this);QProcess *proces;process_shownew process;// 设置进度条的最小值和最大值prog…...

【图灵诸葛】jvm笔记
2023年10月23日14:04:44 jvm 1.jdk体系结构图回顾(Av333129672,P1) jdk jre 底层是hotspot jvm 2.java虚拟机内部组成(Av333129672,P2) 堆 方法区 执行引擎 类加载 本地方法栈 线程栈(虚拟机栈) 3.java虚拟机栈讲解(Av333129672,P3) 程序计数器…...

数据安全小课堂开讲啦!看这里!
数据安全小课堂开讲啦!看这里! 1、什么是数据? 《数据安全法》第三条明确,本法所称的数据,就是指任何以电子或者其他方式对信息的记录。小到个人使用手机、电脑等电子产品时浏览的网页、下载的应用、存储的文件&…...
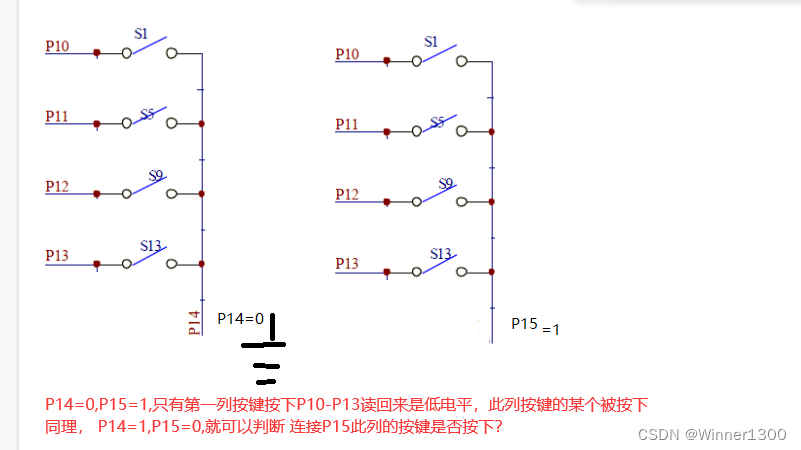
单片机矩阵键盘
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、什么是矩阵键盘?1.独立键盘2.矩阵键盘变化1变化2变化3 3. 通过变型,举一反三,就可以实现4*4的矩阵键盘扫描 二、使用步骤…...
横坐标日期等间隔绘图 python示例代码
有两列数据,一列是日期,另一列是数值。日期是递增的,但是间隔不是均匀的。比如1月1日至2月1日有10组数据,2月1日至3月1日有100组数据,3月1日至4月1日有1000组数据。我想绘折线图,横坐标是日期,纵…...

photoshop2024免费插件Portraiture3
随着手机摄影的普及,修图可以说是现代人的必备生活技能之一了,现在谁发个朋友圈不把自己的照片修的美美的呢?那么如何拥有一张氛围感满满的照片呢?这不得不提图片处理软件中的王牌——photoshop。作为专业的图片处理软件ÿ…...
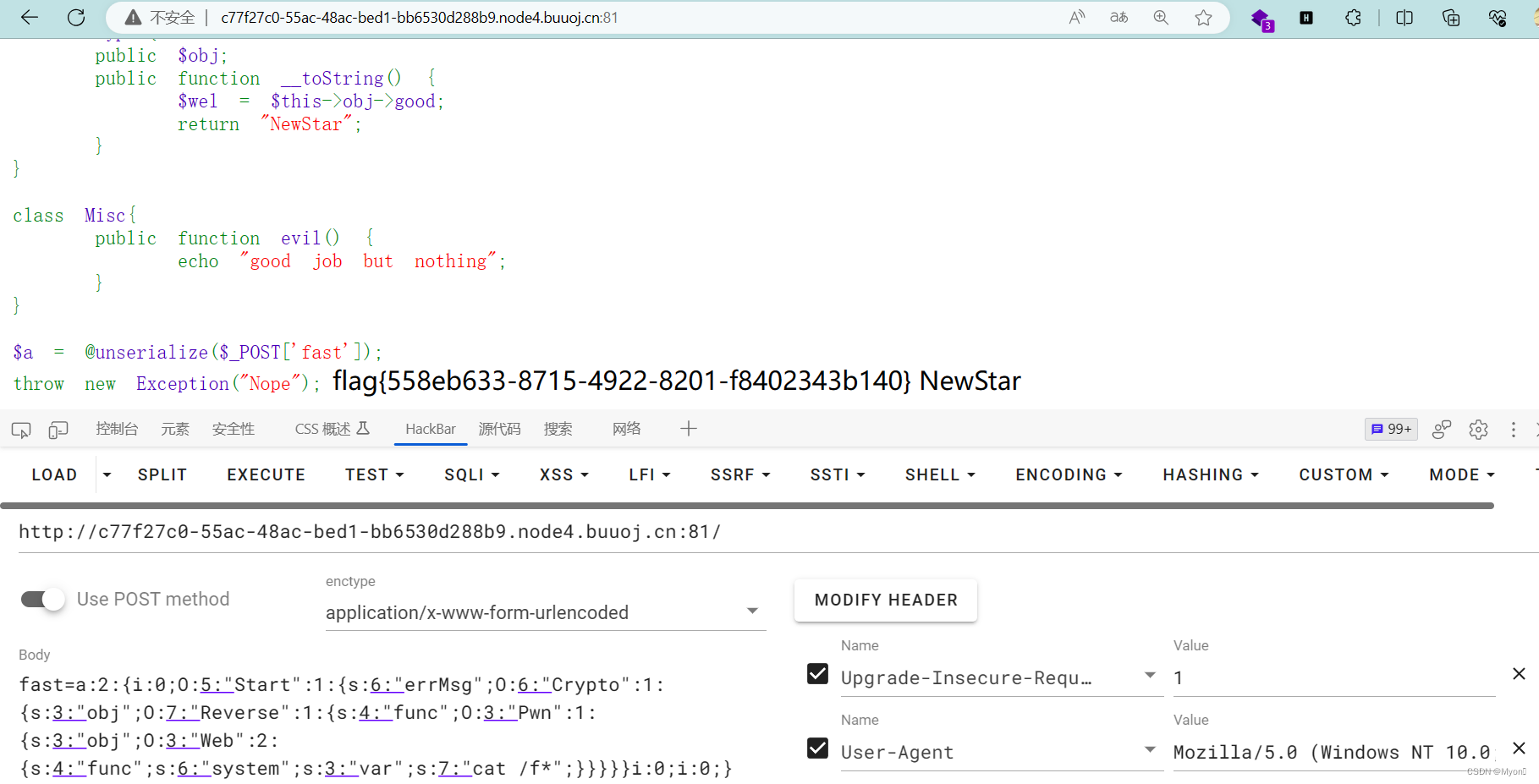
NewStarCTF2023week4-More Fast(GC回收)
打开链接,存在很多个类,很明显是php反序列化漏洞利用,需要构造pop链 , 关于pop链构造的详细步骤教学,请参考我之前的博客,真的讲得很详细也容易理解: http://t.csdnimg.cn/wMYNB 如果你是刚接…...

和鲸赞助丨第16届中国R会议暨2023 X-AGI大会通知
第16届中国 R 会议暨2023 X-AGI大会将于11月25-30日在中国人民大学召开,探讨数据科学和人工智能的相关进展,本次会议将采用线上会议和线下会议相结合的方式举办。 在过去的15年里,中国R会议一直致力于探讨数据科学在各学科、各行业的探索和实…...
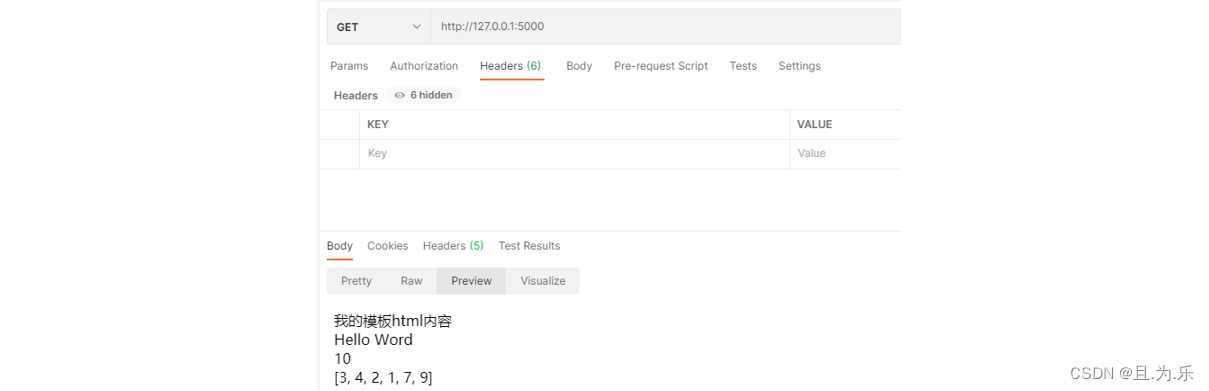
Python第三方库 - Flask(python web框架)
1 Flask 1.1 认识Flask Web Application Framework( Web 应用程序框架)或简单的 Web Framework( Web 框架)表示一个库和模块的集合,使 Web 应用程序开发人员能够编写应用程序,而不必担心协议,线…...

c# sqlite 修改字段类型
因为sqlite不支持直接修改字段类型, 所以只能创建新的表,再将原始数据复制过去。具体操作步骤如下: 第一步, 将表“tableName”的名称修改为 “oldTable” string queryString string.Format("ALTER TABLE {0} RENAME TO …...

[Pytorch] 保存模型与加载模型
1、保存模型 # 定义模型 model BPNetModel(n_featuren_feature,n_hiddenn_hidden,n_outputn_output) #调用网络# 保存模型 torch.save(model, BPNetModel0.pth) 2、加载模型 import torch## 读取模型 model torch.load(BPNetModel0.pth) 3、保存模型参数 #调用网络 mode…...

AES解密报错,Input length must be multiple of 16 when decrypting with padded cipher
# 项目场景:对登录用户名、密码前端加密,后端解密失败 --- # 问题描述 在做login登录页面的用户名和密码加密时,前端加密后端解密,但是抛出`报错:Input length must be multiple of 16 when decrypting with padded cipher`,仔细检查过偏移向量,没有问题,但还是不行,…...

电子学会C/C++编程等级考试2023年05月(三级)真题解析
C/C等级考试(1~8级)全部真题・点这里 第1题:找和为K的两个元素 在一个长度为n(n < 1000)的整数序列中,判断是否存在某两个元素之和为k。 输入 第一行输入序列的长度n和k,用空格分开。 第二行输入序列中的n个整数&am…...

【2023_10_21_计算机热点知识分享】:机器学习中的神经网络
今天的分享主题是机器学习中的神经网络。神经网络是一种模拟人类神经系统的计算模型,它由一系列的神经元组成,每个神经元接收一组输入,经过计算后产生一个输出。神经网络的学习过程是通过调整神经元之间的连接权重来实现的,这个过…...
app开发者提升第四季度广告收入的方法
第四季度将迎来双十一、双十二、圣诞、元旦为主的电商购物季,这是一年中利用线上消费为全新年度和全新预算做好准备的最佳时机,从过往的变现成功案例中汇总了优化要点,帮助开发者在第四季度和未来一年获取更多广告收益。 https://www.shensh…...
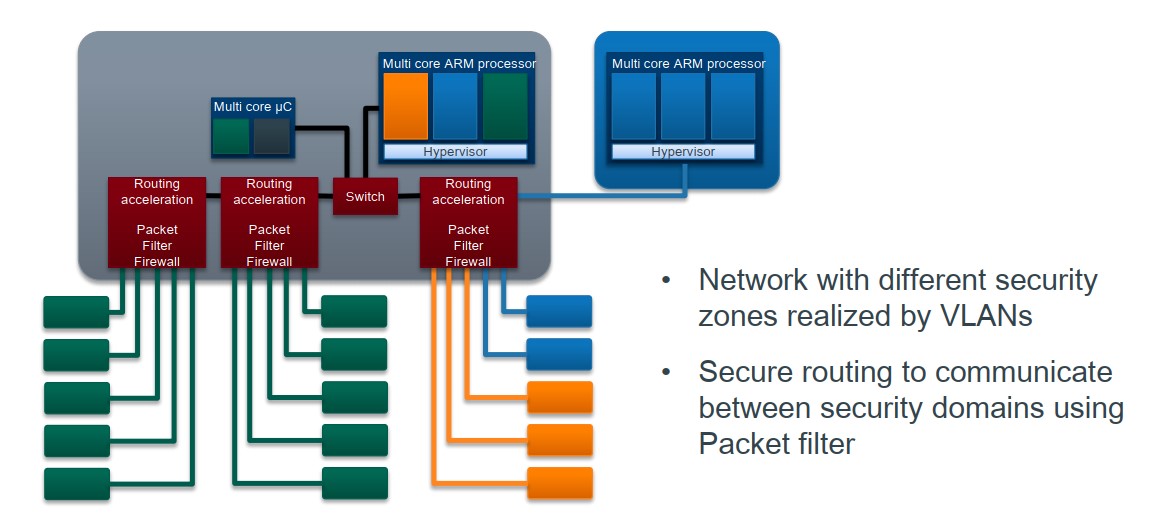
#电子电器架构 —— 车载网关初入门
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 PS:小细节,本文字数7000+,详细描述了网关在车载框架中的具体性能设置。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 没有人关注你。也无需有人关注你。你必须承认自己的价值,你不能站在他…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
