计算机算法分析与设计(20)---回溯法(0-1背包问题)
文章目录
- 1. 题目描述
- 2. 算法思路
- 3. 例题分析
- 4. 代码编写
1. 题目描述
对于给定的 n n n 个物品,第 i i i 个物品的重量为 W i W_i Wi,价值为 V i V_i Vi,对于一个最多能装重量 c c c 的背包,应该如何选择放入包中的物品,使得包中物品的总价值最大?
2. 算法思路
1. 将问题转化为:

2. 按照上述思路,先将各物品按照单位价值递减的顺序排序,其次进行判断是否在承重范围值内。
定义: c w cw cw(current weight)表示当前重量, c p cp cp(current price)表示当前价值。
根节点代表扩展结点 ,其余每一层代表一个物品,越靠近根节点,单位价值越高。选中该物品,即搜索左子树,进行判断。具体执行操作如下所示:
(1)先计算所有物品的单位价值,将其进行降序排列。
(2)排列之后,从根节点(扩展节点)出发。
(3)搜索左子树,判断是否满足约束条件(物品是否装入背包):
若选中该物品(可行解),cw+=w[i],cp+=p[i],继续向下遍历;直至遇到不可行解时,开始向上回溯,取出最后一个装入的物品,进入右子树。
(4)进入右子树,首先计算当前节点的上界bound(i):
若bound(i)小于bestp,剪去右子树,继续向上回溯;否则进行步骤(3)。
(5)遇到叶子节点,比较当前价值与bestp,若cp>bestp,则bestp进行更新。
(6)直到遍历完所有的节点(除剪枝部分外)。
3. 例题分析
1. 例题1(手写):


2. 例题2:假设 n = 3 n=3 n=3(有三件物品),三个物品的重量为 20 、 15 、 10 {20、15、10} 20、15、10,三个物品的价值为 20 、 30 、 25 {20、30、25} 20、30、25,对于一个最大承重为 25 25 25 的背包,求包中物品的组合最大的价值是多少?

3. 例题2分析过程:对三件物品分别进行编号 1 , 2 , 3 1,2,3 1,2,3。初始情况背包是空的。
(1)首先我们把 1 1 1 号物品放进背包里,此时背包里只有一件物品,总重量为 0 + 20 = 20 0+20=20 0+20=20,没有超过承重 25 25 25,因此可以将 1 1 1 号物品成功放入背包内。
(2)接下来尝试把 2 2 2 号物品放入背包内,但是发现包中 1 1 1 号物品和 2 2 2 号物品的重量和为 20 + 15 = 35 20+15=35 20+15=35,超过了承重 25 25 25,因此不能把 2 2 2 号物品放入背包内。
(3)接着考虑 3 3 3 号物品,此时包中只有 1 1 1 号物品。发现 1 1 1 号物品和 3 3 3 号物品的重量和为 20 + 10 = 30 20+10=30 20+10=30,超过了承重 25 25 25,因此 3 3 3 号物品也不能放入背包内。
(4)由于只有 3 3 3 件物品,并且对于每一种物品我们都考虑过是否将其放入背包内,也就是找到了一种基本情况。找到一个基本情况后,我们就可以看看包里的物品的总价值了。这里包里只有一个 1 1 1 号物品,因此总价值为 20 20 20。
(5)重点来了!回溯过程:每次找出一种满足条件的基本情况就进行一次回溯,找到最后放入包中的物品并将其取出,接着考虑是否放入编号在这个物品之后的第一个物品。这里我们就把 1 1 1 号物品取出,接下来考虑是否放入 2 2 2 号物品。
(6)取出 1 1 1 号物品后背包是空的,此时如果放入 2 2 2 号物品,背包总重量为 15 15 15,没有超过背包承重,因此把 2 2 2 号物品放入背包内。
(7)类似地,考虑将 3 3 3 号物品放入背包内。由于 2 2 2 号物品和 3 3 3 号物品的重量和为 15 + 10 = 25 15+10=25 15+10=25,没有超过承重 25 25 25,因此将其放入背包内。
(8)由于考虑完了 3 3 3 号物品,因此又找到了一个基本情况,记下此时包里物品的总价值,为 30 + 25 = 55 30+25=55 30+25=55。由于 55 55 55 高于上一种基本情况的总价值,因此将最优解更新为 55 55 55。
(9)进行一次回溯,取出背包中最后放入的物品,也就是 3 3 3 号物品。但是注意:当最后放入背包中的物品恰好是编号最大的物品时,需要额外进行一次回溯。为什么呢?因为编号最大的物品之后已经没有编号更大的物品了,因此没有可以考虑的下一种情况,只能在上一个层面上在进行一次回溯才能产生可能的最优解(此处不必考虑只放入2号物品的情况,因为一定不是最优解,原因可以自己思考一下)。 这里再回溯一次,也就是将倒数第二个放入包中的物品取出来,这里就取出 2 2 2 号物品。先后取出 3 3 3 号物品和 2 2 2 号物品之后包应该处于空的状态。
(10)上一步中取出了 2 2 2 号物品,因此这一步直接考虑能否放入 3 3 3 号物品,简单的判断后即可得出可以放入,并且同上理也可以得出这是一种基本情况。但是由于包中只有 3 3 3 号物品,总价值为 25 25 25,没有超过当前的最优解 55 55 55,因此将该情况忽略。
(11)最后一次回溯,取出包中的 3 3 3 号元素。由于此时包已经空了,并且最后一次取出的是编号最大的元素,那么说明算法已经完成了所有情况的遍历,算法终止, 55 55 55 是最优解。
4. 代码编写
// n=5, c=10, w={2, 2, 6, 5, 4}, v={6, 3, 5, 4, 6}的0-1背包问题的最优解和最优值。
#include <iostream>
using namespace std;#define N 10
int w[N]; //重量
int v[N]; //价值
int x[N]; //1表放入背包,0表不放入
int n,c; //n:物品个数 c:背包的最大容量int cw=0; //当前物品总重
int cv=0; //当前物品总价值int bestp=0; //当前最大价值
int bestx[N]; //最优解//回溯函数 k表示当前处在第几层做选择,k=1时表示决定是否将第一个物品放入背包
void backtrack(int k)
{//叶子节点,输出结果if(k>n){//找到一个更优的解if(cv>bestp){ //保存更优的值和解bestp = cv;for(int i=1; i<=n; i++)bestx[i] = x[i];}}else{//遍历当前节点的子节点for(int i=0; i<=1; i++){x[k]=i;if(i==0){backtrack(k+1);}else{ //约束条件:当前物品是否放的下if((cw+w[k])<=c){cw += w[k];cv += v[k];backtrack(k+1);cw -= w[k];cv -= v[k];}}}}
}int main()
{cout<<"请输入物品的个数:";cin>>n;cout<<"请输入每个物品的重量及价值:"<<endl;for(int i=1;i<=n;i++){cin>>w[i]>>v[i];}cout<<"请输入背包的限制容量:";cin>>c;backtrack(1);cout<<"最优值是:"<<bestp<<endl;cout<<"(";for(int i=1;i<=n;i++){cout<<bestx[i]<<" ";} cout<<")";return 0;
}

相关文章:

计算机算法分析与设计(20)---回溯法(0-1背包问题)
文章目录 1. 题目描述2. 算法思路3. 例题分析4. 代码编写 1. 题目描述 对于给定的 n n n 个物品,第 i i i 个物品的重量为 W i W_i Wi,价值为 V i V_i Vi,对于一个最多能装重量 c c c 的背包,应该如何选择放入包中的物品…...

什么是IO多路复用?Redis中对于IO多路复用的应用?
IO多路复用是一种高效的IO处理方式,它允许一个进程同时监控多个文件描述符(包括套接字、管道等),并在有数据可读或可写时进行相应的处理。这种机制可以大大提高系统的并发处理能力,减少资源的占用和浪费。 在Redis中&…...

NanoPC-T4 RK3399:DTS之io-domain,FAN
前言: 之后所有改动均是基于rk3399-evb.dts修改以满足NanoPC-T4功能正常。 NanoPC-T4开发板上有一片散热风扇,本章将讲述使风扇正常工作起来的多种方法。 一:硬件分析 GPIO4_C6/PWM1:实际控制风扇引脚,GPIO与PWM复用 输入高电平1:FAN2pin电路导通,风扇转动 输入低电…...

vue3+vite+ts项目使用jQuery
1、安装jQuery npm install --save jquery 2、安装声明文件 npm install --save types/jquery 3、在需要的文件中引入 import $ from jquery...
一起学数据结构(10)——排序
从本文开始,通过若干篇文章展开对于数据结构中——排序的介绍。 1. 排序的概念: 将一堆杂乱无章的数据,通过一定的规律顺序排列起来。即将一个无序序列排列成一个有序序(由小到大或者由大到小)的运算。 在数据的排序中…...
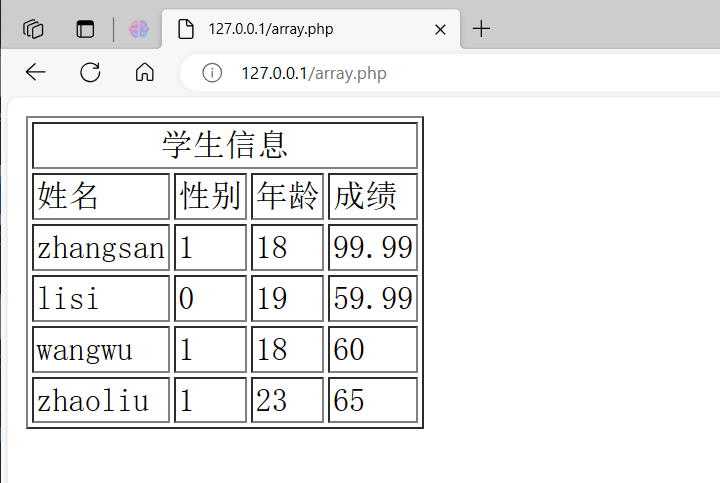
php 数组基础/练习
数组 练习在最后 数组概述 概述与定义 数组中存储键值对 数组实际上是一个有序映射 key-value,可将其当成真正的数组、列表(向量)、散列表、字典、集合、栈、队列等 数组中的元素可以是任意类型的数据对象(可以嵌套数组&#…...
Redbook Chapter 7: Query Optimization翻译批注
首先说明一下redbook上的几篇文章是做什么的。这几篇文章是通过几位作者对不同方面的论文进行阅读和筛选后,挑出其中具备代表性或者权威的论文来做分析,为读者提供阅读指导和建议,同时,也是对某个方面的论文进行高度的总结&#x…...
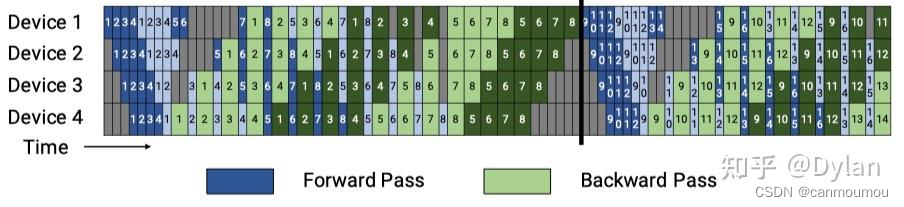
【分布式】大模型分布式训练入门与实践 - 04
大模型分布式训练 数据并行-Distributed Data Parallel1.1 背景1.2 PyTorch DDP1) DDP训练流程2)DistributedSampler3)DataLoader: Parallelizing data loading4)Data-parallel(DP)5)DDP原理解析…...

欧拉图相关的生成与计数问题探究
最近学了一波国家集训队2018论文的最后一个专题。顺便带上了一些我的注解。 先放一波这个论文 1.基本概念 欧拉图问题是图论中的一类特殊的问题。在本文的介绍过程中,我们将会使用一些图 论术语。为了使本文叙述准确,本节将给出一些术语的定义。 定义…...
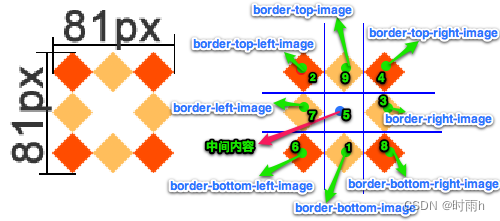
CSS3属性详解(一)文本 盒模型中的 box-ssize 属性 处理兼容性问题:私有前缀 边框 背景属性 渐变 前端开发入门笔记(七)
CSS3是用于为HTML文档添加样式和布局的最新版本的层叠样式表(Cascading Style Sheets)。下面是一些常用的CSS3属性及其详细解释: border-radius:设置元素的边框圆角的半径。可以使用四个值设置四个不同的圆角半径,也可…...

小程序:如何合理规划分包使主包不超过2M
背景 做过小程序项目的同学应该都有这样的经历,项目做着做着,突然发现代码包的大小超过了 2M,小程序无法提审,然后痛苦的删文件改代码来减少包大小。 虽然我们也知道小程序给我们提供了分包的功能可以减少主包的大小,…...

迭代器的封装与反向迭代器
一、反向迭代器 在list模拟实现的过程中,第一次接触了迭代器的封装,将list的指针封装成了一个新的类型,并且以迭代器的基本功能对其进行了运算符重载 反向迭代器是对正向迭代器的封装,并且体现了泛型编程的思想,任意…...

PHP项目学习笔记-萤火商城https://www.yiovo.com/doc
萤火商城学习笔记 注意事项关于建表增加页面流程前台页面的数据列表数据下拉列表的数据 关于时间的处理前台界面数据处理 多年没有碰过php代码了,这个项目不错,想好好学习下,持续更新 注意事项 打开APP_DEBUG有些时候改了前台页面后&#x…...

我国有多少个港口?
港口是什么? 港口是海洋运输中不可或缺的重要设施之一,是连接陆路和水路运输的重要节点。港口通常是指位于沿海地区的水陆交通枢纽,是船舶停靠、装卸货物、储存物资和维修船只的场所。港口一般由码头、泊位、仓库、货场、客运站等设施组成&a…...
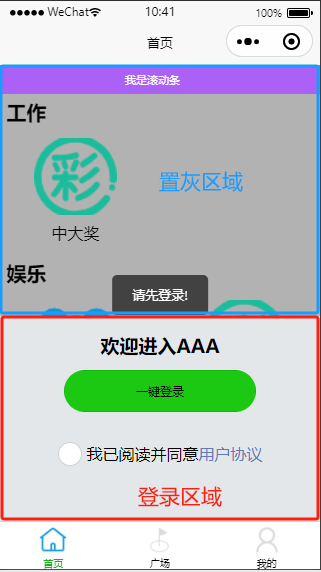
uniapp实现登录组件之外区域置灰并引导登录
实现需求 每个页面需要根据用户是否登录决定是否显示登陆组件,登录组件半屏底部显示,登录组件之外区域置灰,功能按钮点击之后引导提示登录.页面效果如下: 实现思路说明 设置登录组件背景颜色为灰色,将页面分成登录区域(底部)和非登陆区域(上面灰色显示部分), 置灰区域添加…...
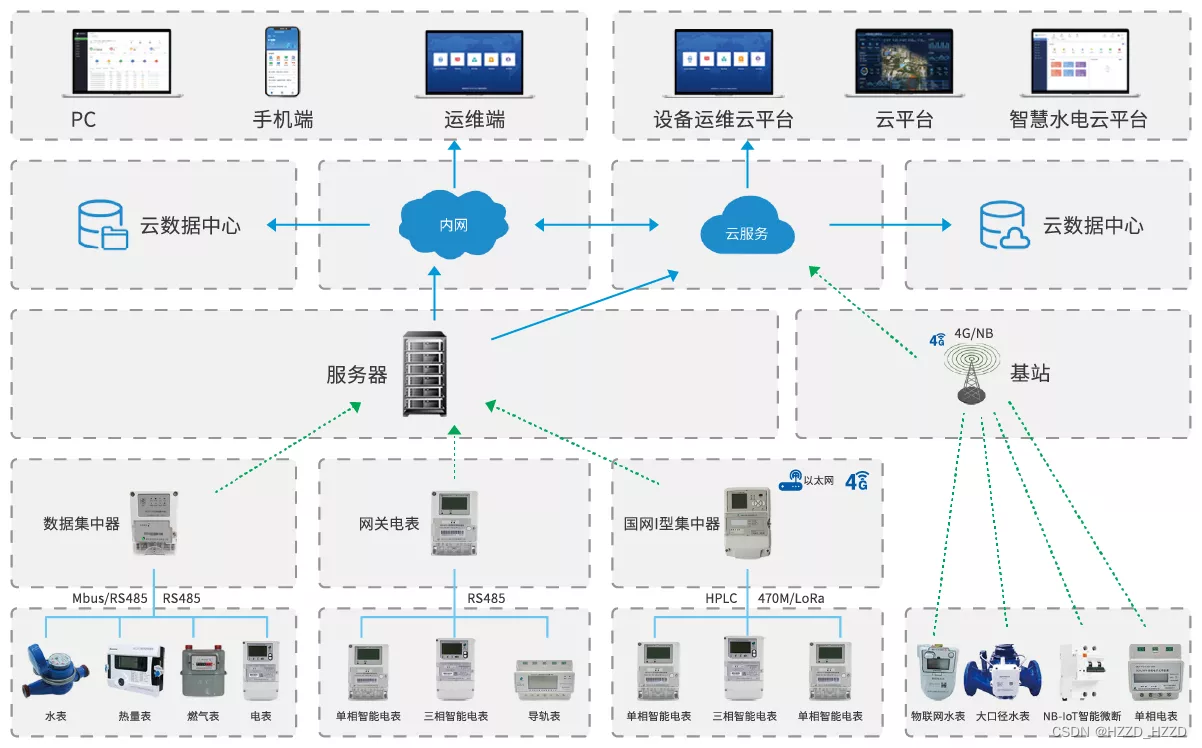
抄表系统是如何抄到电表水表的数据的?
抄表系统是一种利用无线通信技术,实现远程读取电表水表数据的系统。抄表系统主要由三部分组成:电表水表、集中器和后台管理平台。接下来,小编来为大家详细的介绍下抄表系统是如何抄到电表水表的数据的,一起来看下吧! 电表水表是抄…...
Qt之自定义事件QEvent
在Qt中,自定义事件的步骤大概如下: 1.创建自定义事件,自定义事件需要继承QEvent 2.使用QEvent::registerEventType()注册自定义事件类型,事件的类型需要在 QEvent::User 和 QEvent::MaxUser 范围之间,在QEvent::User之前是预留给系统的事件 3.使用sendEvent() 和 postEv…...

项目管理week5——交个作业
...

5.5G移动通信技术
5.5G即5G-Advanced,是一种移动通信技术。 5.5G 是 5G 和 6G 之间的过渡阶段,将在速率、时延、连接规模和能耗方面全面超越现有 5G,有望实现下行万兆和上行千兆的峰值速率、毫秒级时延和低成本千亿物联。按照国际标准组织 3GPP 定义ÿ…...

chrony时间服务
目录 1.1.重要性 1.2. Linux的两个时钟 1.3. NTP 1.4. Chrony介绍 2.安装与配置 2.1.安装: 2.2. Chrony配置文件分析 3.实验 3.1实验1 3.2实验2 3.常见时区 1.1.重要性 ●由于IT系统中,准确的计时非常重要,有很多种原因需要准确计时: 。在网络…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
