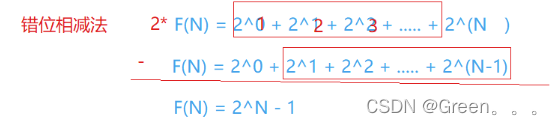【数据结构初阶】算法的时间复杂度和空间复杂度
算法的时间复杂度和空间复杂度
- 1.算法效率
- 1.1 如何衡量一个算法的好坏
- 1.2 算法的复杂度
- 2.时间复杂度
- 2.1 时间复杂度的概念
- 2.2 大O的渐进表示法
- 2.3常见时间复杂度计算举例
- 3.空间复杂度
- 4. 常见复杂度对比
1.算法效率
1.1 如何衡量一个算法的好坏
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列:
long long Fib(int N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
1.2 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2.时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3常见时间复杂度计算举例
实例一:
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
O(N)
实例1基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
实例二:
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
O(N+M)
实例2基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
实例三:
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
O(1)
实例3基本操作执行了10次,通过推导大O阶方法,时间复杂度为 O(1)
实例四:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );//str中查找一个字符串
实例4基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
实例五:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
O(N^2)
实例5基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最
坏,时间复杂度为 O(N^2)
实例六:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
O(logN)
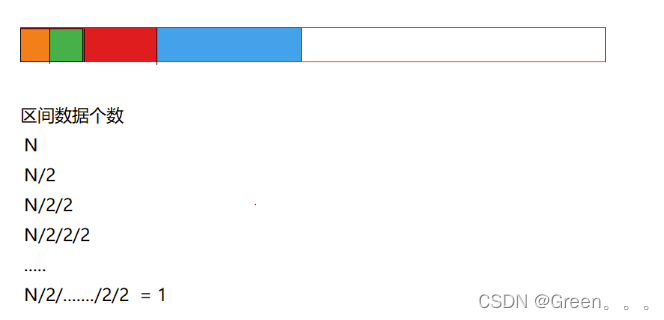
实例6基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN) ps:logN在算法分析中表示是底
数为2,对数为N。有些地方会写成lgN。(建议通过折纸查找的方式讲解logN是怎么计算出来的)
实例七:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
O(N)
实例7通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。
总结:递归算法时间复杂度是多次调用次数累加
实例八:
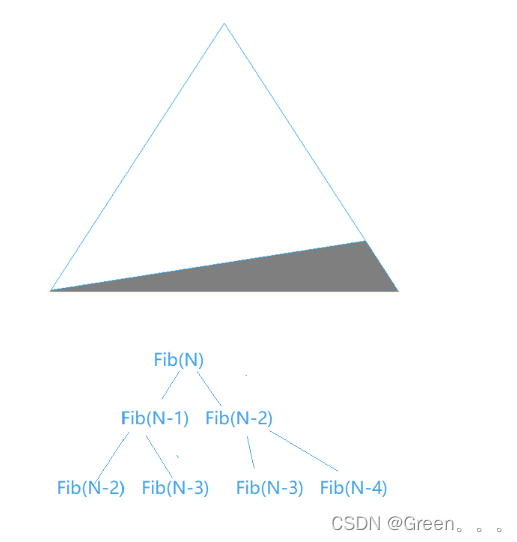
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
实例8通过计算分析发现基本操作递归了2^N 次,时间复杂度为O(2^N)。(建议画图递归栈帧的二叉树讲解)
补:
3.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因
此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
案例一:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
实例1使用了常数个额外空间(int n,int exchange,int end),所以空间复杂度为 O(1)
实列二:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}
实例2动态开辟了N个空间,空间复杂度为 O(N)
实例三:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
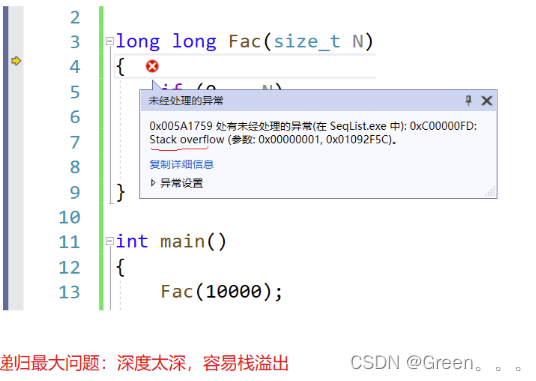
实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
时间一去不复返,空间可重复利用->了解函数栈帧
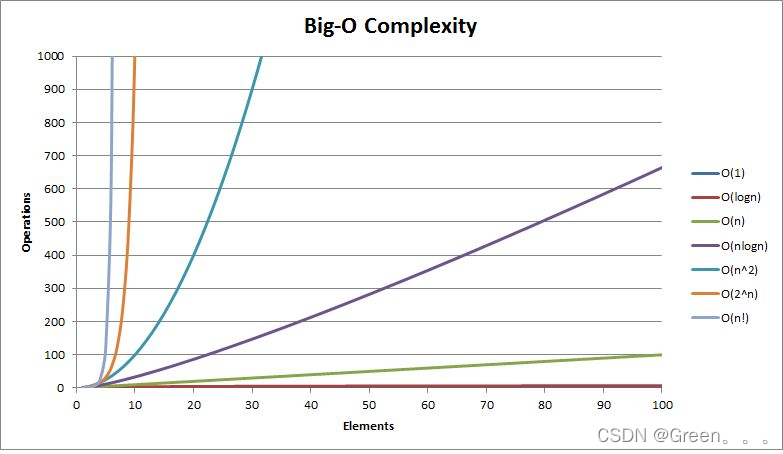
4. 常见复杂度对比
一般算法常见的复杂度如下
💘不知不觉,【数据结构初阶】算法的时间复杂度和空间复杂度以告一段落。通读全文的你肯定收获满满,让我们继续为数据结构学习共同奋进!!!
相关文章:
【数据结构初阶】算法的时间复杂度和空间复杂度
算法的时间复杂度和空间复杂度 1.算法效率1.1 如何衡量一个算法的好坏1.2 算法的复杂度 2.时间复杂度2.1 时间复杂度的概念2.2 大O的渐进表示法2.3常见时间复杂度计算举例 3.空间复杂度4. 常见复杂度对比 1.算法效率 1.1 如何衡量一个算法的好坏 如何衡量一个算法的好坏呢&am…...

git log 命令详解
测试仓库 asdf 常用参数 查询指定目录 git -C /Users/yanlp/workspace/asdf log 限制显示提交数量 git log -n 3 限制提交人|邮箱 git log --authorEdwin Kofler | git log --authoredwinkofler.dev 限制一个月内的提交git log --since1.month.ago | git log --since2023-0…...

docker运行elastic和kibana,并使用密码连接
1. elasticsearch 运行容器 docker run -d --name elasticsearch -p 9200:9200 -p 9300:9300 -e "discovery.typesingle-node" elasticsearch:7.7.0 进入容器 docker exec -it elasticsearch bash修改配置开启密码校验 vi ./conf/elasticsearch.yml添加以下内容 …...

前端html生成PDF
需要用到的组件 1、html2canvas 地址:http://html2canvas.hertzen.com/ 安装:npm install --save html2canvas 2、jsPDF 地址:https://github.com/parallax/jsPDF 安装:npm install jspdf --save 代码 // 导出页面为PDF格式 im…...

强化学习代码实战(3) --- 寻找真我
前言 本文内容来自于南京大学郭宪老师在博文视点学院录制的视频,课程仅9元地址,配套书籍为深入浅出强化学习 编程实战 郭宪地址。 正文 我们发现多臂赌博机执行一个动作之后,无论是选择摇臂1,摇臂2,还是摇臂3之后都会返…...

SA+ST表维护height+单调队列维护:CF1073G
https://www.luogu.com.cn/problem/CF1073G lcp相关的,先跑个sa,然后height建个ST表 现在考虑询问,我们按A和B按 r k rk rk 排序。现在考虑B->A,反过来同理。 我们可以用单调队列维护,满足height是单增的。因为…...

Java中JVM、JRE和JDK三者有什么区别和联系?
任何语言或者软件的运行都需要环境。就像人要生活在空气中,鱼要活在水中,喜阴植物就不能放在阳光下暴晒一样,任何对象个体的存在都离不开其所需要的环境,编程语言亦是一样的。 java 语言的开发运行,也离不开 Java 语言…...
秋季期中考复现xj
flow analysis 1 What is the backdoor file name that comes with the server?( Including file suffix) 服务器自带的后门文件是什么?(含文件后缀) 题目还要求最后把那个文件名MD5一下,再去提交 开始的前三题是流量分析的&…...

【代码随想录】算法训练营 第十四天 第六章 二叉树 Part 1
递归遍历 递归法讲究的就是一个格式,在外边再定义一个用于递归求解的函数reverser,参数是递归的二叉树当前根节点和用于保存遍历得到的答案序列的vector容器; 函数中的格式就是,先写递归终止条件,也就是遍历的结点为…...
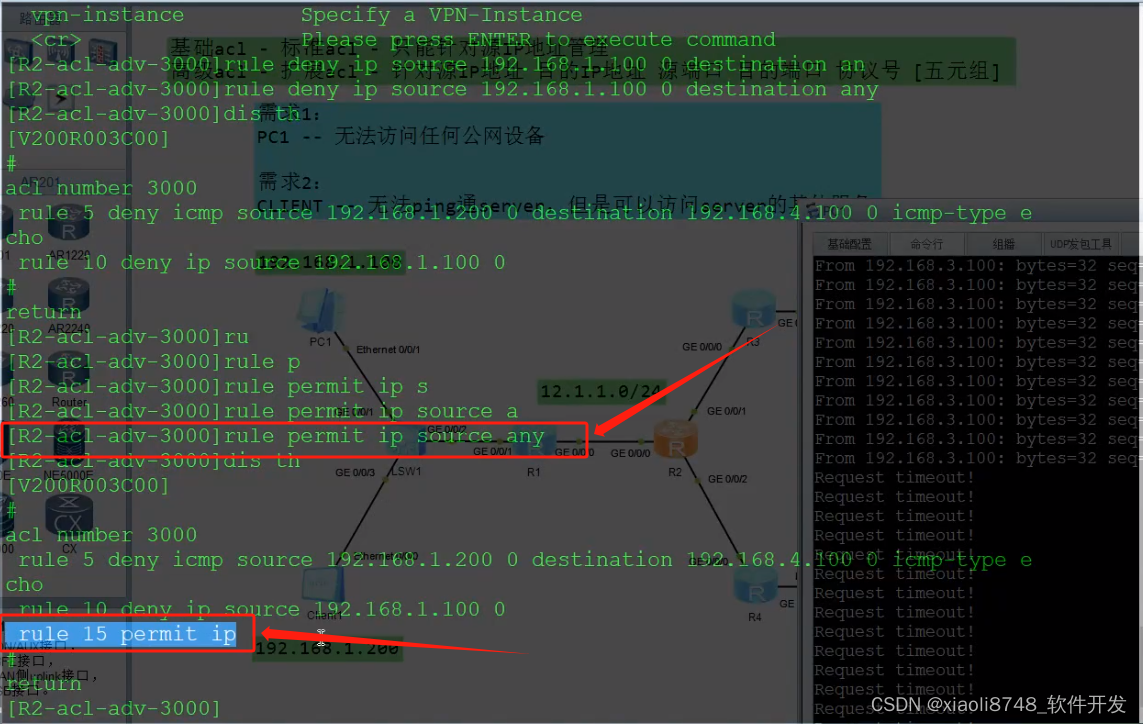
【访问控制】—>《熟练使用ACL进行上网行为管理》
✍ 标准和高级ACL功能介绍; ✍ 思科和华为ACL功能有什么区别? ✍ 现网中ACL都有哪些使用场景? -- ACL - 访问控制列表 - 控制: 能通/不能通 -- ACL - 结合功能 list - 简化版本的行为管理 -- 插件性质的功能 --…...

MySQL外键,表与表的关系,多表查询,Navicat软件
外键 MySQL可以使用外键来保持表之间的关系完整性。 要设置外键,可以按照以下步骤进行操作: 在创建表时,使用FOREIGN KEY关键字来指定外键列: CREATE TABLE table1 (id INT PRIMARY KEY,name VARCHAR(50),table2_id INT,FOREI…...

Linux系统镜像备忘
阿里镜像源: ubuntu ubuntu-releases安装包下载_开源镜像站-阿里云 centos centos-stream安装包下载_开源镜像站-阿里云...

Docker容器端口在主机的映射
Docker容器端口在主机的映射 Docker 允许你在启动容器时进行多个端口映射,以便将容器内部的端口映射到宿主机上的不同端口。你可以使用-p或--publish标志来指定端口映射。以下是一些示例,说明如何在 Docker 启动容器时进行多个端口映射: 映…...
Spring Boot中RedisTemplate的使用
当前Spring Boot的版本为2.7.6,在使用RedisTemplate之前我们需要在pom.xml中引入下述依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId><vers…...

GSCoolink GSV6183 带嵌入式MCU的MIPI D-PHY 转 DP/eDP
Gscoolink GSV6183是一款高性能、低功耗的MIPI D-PHY到DisplayPort/eDP 1.4转换器。通过集成基于RISC-V的增强型微控制器,GSV6183创造了一种具有成本效益的解决方案,提供了上市时间优势。MIPI D-PHY接收器支持CSI-2版本1.3和DSI版本1.3,每条通…...

Linux文件系统 struct dentry 结构体解析
文章目录 前言一、目录项简介二、struct dentry2.1 简介2.2 dentry和inode关联2.3 目录项视图2.4 目录项状态2.5 目录项特点 三、dentry cache3.1 简介3.2 dentry cache 初始化3.3 dentry cache 查看 四、dentry与mount、file的关联五、其他参考资料 前言 这两篇文章介绍了: V…...

C++——vector
目录 vector vector常用接口 构造函数 operator[]size() 迭代器 范围for capacity() resize() reverse() push_back和pop_back insert erase() algorithm::sort 注意 迭代器失效 vector vector单词直译是向量的意思,这个容器可以容纳不同的类型数据&am…...

html5语义化标签
目录 前言 什么是语义化标签 常见的语义化标签 语义化的好处 前言 HTML5 的设计目的是为了在移动设备上支持多媒体。之前网页如果想嵌入视频音频,需要用到 flash ,但是苹果设备是不支持 flash 的,所以为了改变这一现状,html5 …...

SQL Server批量删除数据库中的表
如果想要删除数据库中temp 开头的中间表 1. SQL 语句实现 use [DBName] --todo go select drop table name from sys.tables where name like temp% go 将查询结果粘贴到数据库中运行 2. 数据库 单击目标数据库中的Tables ,然后按F7 键,按Name 进行排序&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...