Educational Codeforces Round 143 (Rated for Div. 2)
Educational Codeforces Round 143 (Rated for Div. 2)
D. Triangle Coloring
思路:
- 每个环都需要取最大值,那么我们讨论一个环获得最大值选的两条边的可能取法: 显然:如果三边相等,这个环有3种取法。如果有两条小边相等,这个环有两种取法。其余情况都只能取一种
- 之后把每个环都看成一个点,就是从n个环选n/2个蓝色(红色),求组合数。
- 所以其实就是考逆元乘法逆元(费马小定理,拓欧,线性dp)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
typedef pair<int, int> pii;//double 型memset最大127,最小128
//std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 2e5 + 10;
const int mod = 998244353;
int a[3];ll fastmi(ll base, ll power)//快速幂求逆元
{ll ans = 1;while (power){if (power & 1)ans = ans * base % mod;base = base * base % mod;power >>= 1;}return ans;
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n;cin >> n;//n从表示一个点转化为表示一个环n /= 3;ll ans = 1;for (int i = 1; i <= n; ++i){cin >> a[0] >> a[1] >> a[2];//3点一个环sort(a, a + 3);//if (a[0] == a[2])ans = (ans * 3) % mod;//else if (a[0] == a[1])ans = (ans * 2) % mod;}ll tmp = 1;for (int i = 1; i <= n / 2; ++i)//求组合数C(n/2,n){ans = (ans * (n / 2 + i)) % mod;tmp = tmp * i % mod;}ans = (ans * fastmi(tmp, mod - 2)) % mod;cout << ans << endl;return 0;
}E. Explosions?
思路:
- 我们枚举每个点作为爆炸点,显然,爆炸连续的前提就是左边生命值严格单调增,右边严格单调减。
- 由于我们需要消耗的生命值总和是恒定的,所以,那个点爆炸造成总伤害高,显然耗费魔法值更少
- 我们考虑爆炸时左边(右边)的邻居(j)与爆炸点(x)的大小关系(a[i]表示生命值,l[i]表示i对左边可以造成的伤害和(包括炸死自己)):
- 会发现,如果a[j]>=a[x]-1,是无法爆炸的,不过,我们可以用单位魔法把j生命值变为a[x]-1,所以无影响
- 所以对于x左边任意点j,如果a[j]>=a[x]-(x-j),我们可以用单位魔法操作到其生命值为a[x]-(x-j)。
- 对于a[j]<a[x]-(x-j),那我们下一次爆炸的威力就减少了,而且我们发现,后续产生的伤害等于l[j],所以我们加上l[j]就不用再往左了
- 因此,我们得出,每次求l[x],只需要找到第一个点j满足a[j]<a[x]-(x-j),那么 l[x]=(x-j)*(a[x]+(a[x]-(x-j)+1)/2+l[j]
- 然而,每个点都回溯太费时间了,我们中间那些不满足a[j]<a[x]-(x-j)的点j只要没用一次就一直没用,我们能不能舍去他,为这个数组减肥呢。
- 观察发现,不等式可以表示为a[j]-j<a[x]-x,所以我们可以另开一个数组记录这个信息。然后从左往右遍历,每次求当前点l[x],只需要把a[j]-j>=a[x]-x的前面点舍去,最后就可以立刻求取答案,显然,舍去这个功能让我们想到可以开一个栈(先进后出)
- 爆炸右边也是同理
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
typedef pair<int, int> pii;//double 型memset最大127,最小128
//std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 3e5 + 10;
int a[N], l[N], r[N], a1[N], n;void cnt(int *f)
{stack<int>s;s.push(0);//放入左边边界外面0for (int i = 1; i <= n; ++i)a1[i] = a[i] - i; //记录比较数组for (int i = 1; i <= n; ++i){while ((int)s.size() > 1 && a1[s.top()] >= a1[i])s.pop(); //从最靠近右边的点(堆顶)开始比较,不满足的点全部舍去,后面也没用了int len = min(a[i], (ll)i - s.top()); //爆炸可持续范围最长是a[i](伤害不断递减),不是直接取遇到满足条件的j点(你可能到不了那个点)f[i] = f[s.top()] + len * (2 * a[i] - len + 1) / 2;s.push(i);//不断给栈存入新的点}
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t;cin >> t;while (t--){cin >> n;ll sum = 0;for (int i = 1; i <= n; ++i)cin >> a[i], sum += a[i];cnt(l);reverse(a + 1, a + 1 + n); //反转一下求右边爆炸cnt(r);reverse(r + 1, r + 1 + n); //r获得的是反转过的,要反转回来reverse(a + 1, a + 1 + n);ll ans = 0;for (int i = 1; i <= n; ++i)ans = max(ans, l[i] + r[i] - 2 * a[i]); //l与r都记录了a[i]造成的伤害,然而这个伤害是魔法产生的,不是被波及的cout << sum - ans << endl;}return 0;
}相关文章:
)
Educational Codeforces Round 143 (Rated for Div. 2)
Educational Codeforces Round 143 (Rated for Div. 2) D. Triangle Coloring 思路: 每个环都需要取最大值,那么我们讨论一个环获得最大值选的两条边的可能取法: 显然:如果三边相等,这个环有3种取法。如…...

业务代码编写过程中如何「优雅的」配置隔离
思考 不同的处理方式 1.常规的处理方式,通过某种规则判断区分代码环境 // 获取环境标识 const env getCurrentEnv();if (env dev) {// do something } else if (env test) {// do something } else if (env prod) {// do something } 分析: 1.此种…...

English Learning - L2-2 英音地道语音语调 2023.02.23 周四
English Learning - L2-2 英音地道语音语调 2023.02.23 周四查音标的工具怎么练习效果好准备工作大小声练习大元音开口度的对比舌位对比复习后元音 /ɑː/ /ɔː/ /uː//ɑː//ɔː//uː/前元音 /iː/发音技巧对应单词的发音对应句子的发音常见的字母组合中元音 /ɜː/发音技巧…...
和notify())
java:线程等待与唤醒 - Object的wait()和notify()
java:线程等待与唤醒 - Object的wait()和notify() 1 前言 java使用Object类的wait()和notify()方法,可以实现线程等待和唤醒(Object类为所有类的父类,即所有类天然具有线程等待和唤醒的方法,一般使用Object类的wait(…...
实现弹窗功能并修改其中一个系数
把鼠标放在number-info上面,会是一个delon/chart的类库,可以在NG-ALAIN上找到阅读NG ALAIN的图表,以及number-info样式,数据文本 它拥有[title] [subtitle]两个可以是TemplateRef类型的,而template可以在里面放一些东西,比如按钮,所以可以放一个修改按钮 这里刚开始把template放…...
vue-draggable浏览器拖拽event事件对象拖动时 DragEvent path undefined
场景: 在做组件拖拽过程中,需要获取到触发元素冒泡过程中的所有元素,所以使用了event.path属性。在Chrome下正常运行,但是在FireFox下测试时发现,完犊子,失效了,通过问题排查,发现了…...

【云原生】搭建k8s高可用集群—20230225
文章目录多master(高可用)介绍高可用集群使用技术介绍搭建高可用k8s集群步骤1. 准备环境-系统初始化2. 在所有master节点上部署keepalived3.1 安装相关包3.2 配置master节点3.3 部署haproxy错误解决3. 所有节点安装Docker/kubeadm/kubelet4. 部署Kuberne…...

LeetCode121_121. 买卖股票的最佳时机
LeetCode121_121. 买卖股票的最佳时机 一、描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最…...

收割不易,五面Alibaba终拿Java岗offer
前言 前段时间有幸被阿里的一位同学内推,参加了阿里巴巴Java岗位的面试,本人19年双非本科软件工程专业,目前有一年半的工作经验,面试前就职于一家外包公司。如果在自己本人拿到offer之前,如果有人告诉我一年工作经验可…...
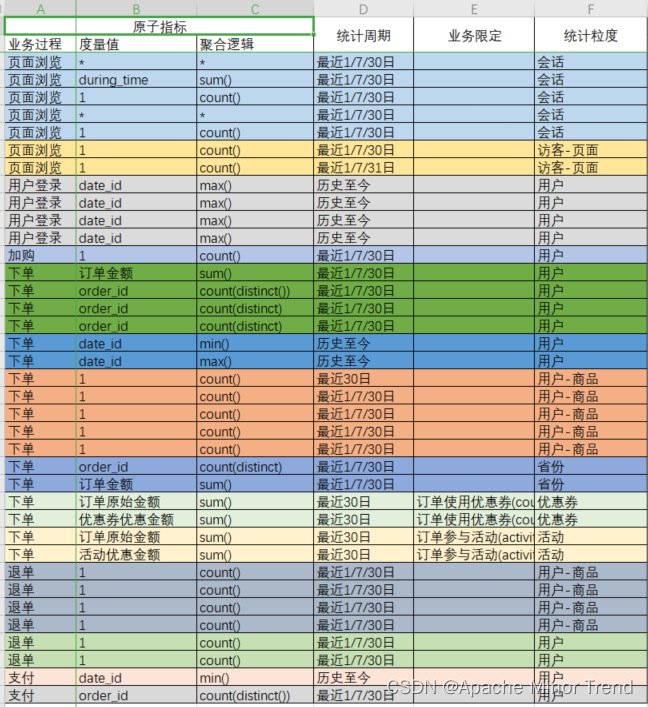
【离线数仓-4-数据仓库设计-分层规划构建流程】
离线数仓-4-数据仓库设计-分层规划&构建流程离线数仓-4-数据仓库设计-分层规划&构建流程1.数据仓库分层规划2.数据仓库构建流程1.数据调研1.业务调研2.需求分析3.总结2.明确数据域3.构建业务总线矩阵&维度模型设计4.明确统计指标1.指标体系相关概念1.原子指标2.派生…...
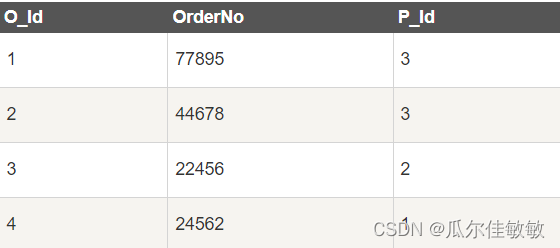
SQL零基础入门学习(十一)
SQL零基础入门学习(十) SQL NOT NULL 约束 NOT NULL 约束强制列不接受 NULL 值。 NOT NULL 约束强制字段始终包含值。这意味着,如果不向字段添加值,就无法插入新记录或者更新记录。 下面的 SQL 强制 “ID” 列、 “LastName” …...
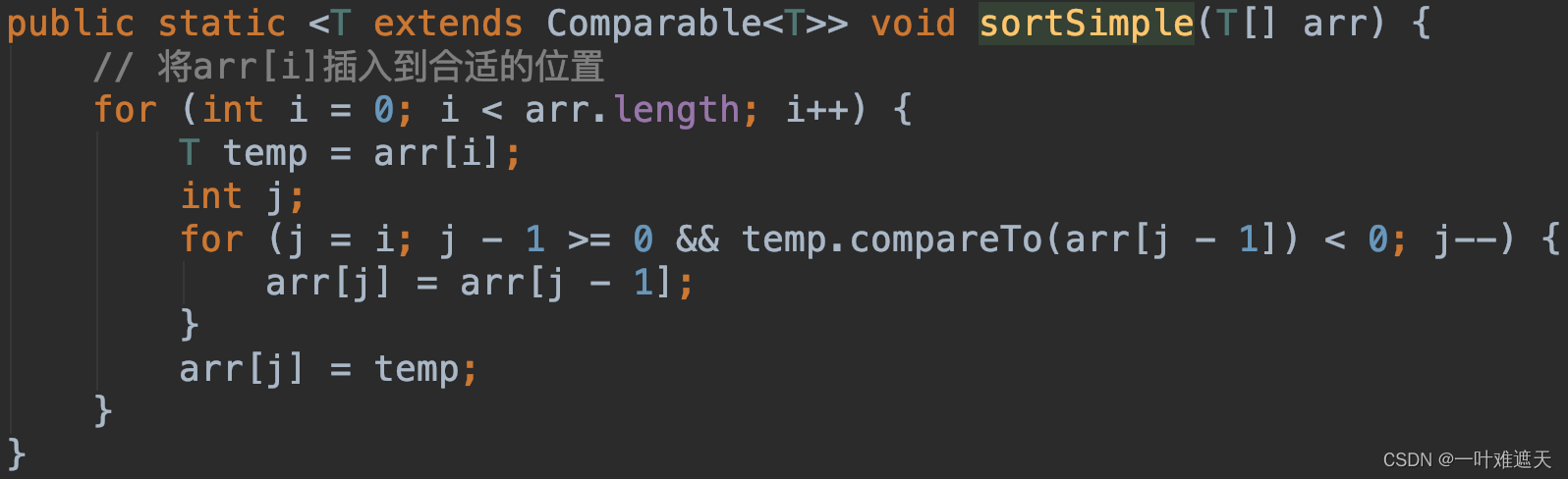
排序基础之插入排序
目录 前言 一、什么是插入排序 二、实现插入排序 三、插入排序优化 四、插入排序的特性 前言 上一篇中我们说到了《排序基础之选择排序》,这一篇我们来学习一下排序算法中的另一种基础排序算法——插入排序。 一、什么是插入排序 简单来说就是:每…...
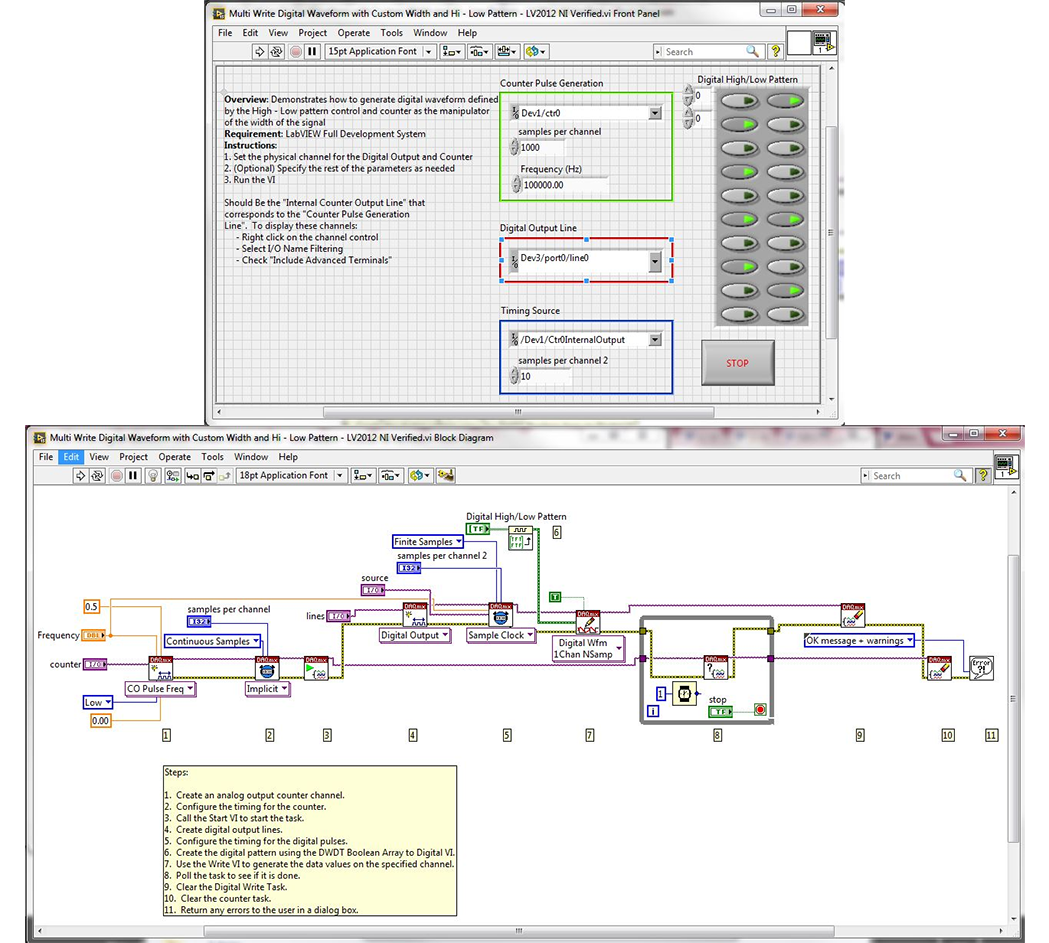
LabVIEW控制DO通道输出一个精确定时的数字波形
LabVIEW控制DO通道输出一个精确定时的数字波形如何使用数据采集板卡的DO通道输出一个精确定时的数字波形?解答:产生一个数字波形首先需要创建一个布尔数组,把波形序列信息放到该布尔数组中,然后通过一个布尔数组至数字转换vi来产生数字波形。…...
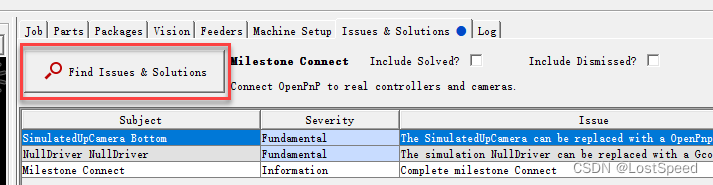
openpnp - 零碎记录
文章目录openpnp - 零碎记录概述笔记配置文件保存无效必须在查找问题之后, 才能保存配置文件如果想找出配置动作引起的配置内容变化, 还是要尝试保存后, 比对变化才行ENDopenpnp - 零碎记录 概述 这段时间, 正在配置校准手头的openpnp设备, 用的官网最新的openpnp2.0. 由于o…...

Qt编写微信支付宝支付
文章目录一 微信支付配置参数二 支付宝支付配置参数三 功能四 Demo效果图五 体验地址一 微信支付配置参数 微信支付API,需要三个基本必填参数。 微信公众号或者小程序等的appid;微信支付商户号mchId;微信支付商户密钥mchKey; 具…...

LeetCode 剑指 Offer 64. 求1+2+…+n
求 12…n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。 示例 1: 输入: n 3 输出: 6 限制: 1 < n < 10000 解法一:利用逻辑运算符的短路…...

Mapper代理开发
MyBatis快速开发https://blog.csdn.net/weixin_51882166/article/details/129204439?spm1001.2014.3001.5501 使用Mapper代理方式完成 定义与SQL映射文件同名的Mapper接口 ,将Mapper接口和SQL映射文件放置同一目录结构 新建接口和包: 将Mapper接口和…...

为什么在连接mysql时,设置 SetConnMaxIdleTime 没有作用
目录测试1go 1.15.15go 1.17.12测试2go 1.15.15go 1.17.12参考在使用golang 连接 mysql时,为了节省连接资源,在连接使用过后,希望在指定长度时间不再使用后,自动关闭连接。 这时,经常会使用SetConnMaxLifetime()&#…...

嵌入式开发利器
前言 俗话说,工欲善其事必先利其器,做嵌入式开发首先需要选择好的工具,对的工具,工具选对了能事半功倍,节省很多时间,那些开发大佬一般都会使用各种各样的工具,不同的环节使用不同的工具&#…...

Qt 的QString类的使用
Qt的QString类提供了很方便的对字符串操作的接口。 使某个字符填满字符串,也就是说字符串里的所有字符都有等长度的ch来代替。 QString::fill ( QChar ch, int size -1 ) 例: QString str "Berlin";str.fill(z);// str "zzzzzz"…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
