【C++代码】安排行程,N皇后,解数独--代码随想录
题目:重新安排行程
-
给你一份航线列表
tickets,其中tickets[i] = [fromi, toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。 -
例如,行程
["JFK", "LGA"]与["JFK", "LGB"]相比就更小,排序更靠前。假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。 -
这道题目有几个难点:
- 一个行程中,如果航班处理不好容易变成一个圈,成为死循环
- 有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
- 使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
- 搜索的过程中,如何遍历一个机场所对应的所有机场。
-
一个机场映射多个机场,机场之间要靠字母序排列,一个机场映射多个机场,可以使用std::unordered_map,如果让多个机场之间再有顺序的话,就是用std::map 或者std::multimap 或者 std::multiset。这样存放映射关系可以定义为
unordered_map<string, multiset<string>> targets或者unordered_map<string, map<string, int>> targets。- unordered_map<string, multiset> targets:unordered_map<出发机场, 到达机场的集合> targets;unordered_map<string, map<string, int>> targets:unordered_map<出发机场, map<到达机场, 航班次数>> targets
- 这两个结构,我选择了后者,因为如果使用
unordered_map<string, multiset<string>> targets遍历multiset的时候,不能删除元素,一旦删除元素,迭代器就失效了。**出发机场和到达机场是会重复的,搜索的过程没及时删除目的机场就会死循环。**所以搜索的过程中就是要不断的删multiset里的元素,那么推荐使用unordered_map<string, map<string, int>> targets。 - 在遍历
unordered_map<出发机场, map<到达机场, 航班次数>> targets的过程中,**可以使用"航班次数"这个字段的数字做相应的增减,来标记到达机场是否使用过了。**如果“航班次数”大于零,说明目的地还可以飞,如果“航班次数”等于零说明目的地不能飞了,而不用对集合做删除元素或者增加元素的操作。
-
class Solution { public:// unordered_map<出发机场, map<到达机场, 航班次数>> targetsunordered_map<string,map<string,int>> targets;bool track(int ticNUM,vector<string> &res){if(res.size()==ticNUM+1){//参数里还需要ticketNum,表示有多少个航班(终止条件会用上)。return true;}// 一定要加上引用即 & target,因为后面有对 target.second 做减减操作,如果没有引用,单纯复制,这个结果就没记录下来,那最后的结果就不对了。for(pair<const string,int>& target:targets[res[res.size()-1]]){if(target.second>0){ // 记录到达机场是否飞过了res.push_back(target.first);target.second--;if(track(ticNUM,res)) return true;res.pop_back();target.second++;}}return false;}vector<string> findItinerary(vector<vector<string>>& tickets) {targets.clear();vector<string> res;for(const vector<string> & vec : tickets){targets[vec[0]][vec[1]]++;}res.push_back("JFK");track(tickets.size(),res);return res;} };
题目:N 皇后
-
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。 -
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
-
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
-
class Solution { public:vector<vector<string>> res;bool isV(int row,int col,vector<string>& board,int n){for(int i=0;i<row;i++){//检查列if(board[i][col]=='Q') return false;}for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){if(board[i][j]=='Q') return false;}for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++)if(board[i][j]=='Q') return false;return true;}void track(int n,int start,vector<string>& board){if(start==n){res.push_back(board);return ;}for(int i=0;i<n;i++){if(isV(start,i,board,n)){board[start][i]='Q';track(n,start+1,board);board[start][i]='.';}}}vector<vector<string>> solveNQueens(int n) {res.clear();vector<string> chessboard(n,string(n,'.'));track(n,0,chessboard);return res;} };
题目:解数独
-
编写一个程序,通过填充空格来解决数独问题。数独部分空格内已填入了数字,空白格用
'.'表示。数独的解法需 遵循如下规则:- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
- 数字
-
本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。回溯三部曲
- 递归函数以及参数:**递归函数的返回值需要是bool类型,**因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
- 递归终止条件:本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
- 递归单层搜索逻辑:在树形图中可以看出我们需要的是一个二维的递归(也就是两个for循环嵌套着递归);一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
-
class Solution { public:bool track(vector<vector<char>>& board){for(int i=0;i<board.size();i++){for(int j=0;j<board[0].size();j++){if(board[i][j]=='.'){for(char k='1';k<='9';k++){if(isV(i,j,k,board)){board[i][j]=k;if(track(board)) return true;board[i][j]='.';}}return false;}}}return true;}bool isV(int row,int col,char k,vector<vector<char>>& chessboard){for(int i=0;i<9;i++){if(chessboard[row][i]==k || chessboard[i][col]==k) return false;} int startR = (row/3)*3;int startC = (col/3)*3;for(int i=startR;i<startR+3;i++){for(int j=startC;j<startC+3;j++){if(chessboard[i][j]==k) return false;}} return true;}void solveSudoku(vector<vector<char>>& board) {track(board);} }; -
回溯是递归的副产品,只要有递归就会有回溯,所以回溯法也经常和二叉树遍历,深度优先搜索混在一起,因为这两种方式都是用了递归。回溯法就是暴力搜索,并不是什么高效的算法,最多再剪枝一下。
-
回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
-
回溯法确实不好理解,所以需要把回溯法抽象为一个图形来理解就容易多了,在后面的每一道回溯法的题目我都将遍历过程抽象为树形结构方便大家的理解。
-
子集问题分析:
- 时间复杂度: O ( 2 n ) O(2^n ) O(2n),因为每一个元素的状态无外乎取与不取,收集树的节点
- 空间复杂度:O(n),递归深度为n,所以系统栈所用空间为O(n),每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为O(n)
-
排列问题分析:
- 时间复杂度:O(n!),这个可以从排列的树形图中很明显发现,每一层节点为n,第二层每一个分支都延伸了n-1个分支,再往下又是n-2个分支,所以一直到叶子节点一共就是 n * n-1 * n-2 * … 1 = n!。
- 空间复杂度:O(n),和子集问题同理。
-
组合问题分析:
- 时间复杂度: O ( 2 n ) O(2^n) O(2n),组合问题其实就是一种子集的问题,所以组合问题最坏的情况,也不会超过子集问题的时间复杂度。
n-1个分支,再往下又是n-2个分支,所以一直到叶子节点一共就是 n * n-1 * n-2 * … 1 = n!。 - 空间复杂度:O(n),和子集问题同理。
- 时间复杂度: O ( 2 n ) O(2^n) O(2n),组合问题其实就是一种子集的问题,所以组合问题最坏的情况,也不会超过子集问题的时间复杂度。
相关文章:

【C++代码】安排行程,N皇后,解数独--代码随想录
题目:重新安排行程 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必…...

SpringCloud Alibaba【二】nacos
nacos配置与使用 nacos初步使用nacos安装与配置创建命名空间 nacos使用与配置创建新项目作为父项目 创建nacos服务端项目pom.xmlapplication.yml启动类 创建nacos客户端项目pom.xml application.yml启动类 启动测试 nacos配置负载均衡改造生产者nacos-provider-projectcontroll…...

C++中的fsanitize指令
一个集成在 gcc、clang 编译器中的编译指令,可以有效测试程序中的一些诸如数组越界、未定义行为等情况。 举个例子: #include <bits/stdc.h> using namespace std;const int maxn2e55,mxr1e5,maxm1e75; int head[maxn],nxt[maxn],to[maxn],f[max…...
【AI视野·今日Robot 机器人论文速览 第五十八期】Thu, 19 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Thu, 19 Oct 2023 Totally 25 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers InViG: Benchmarking Interactive Visual Grounding with 500K Human-Robot Interactions Authors Hanbo Zhang, Jie Xu, Yuch…...

Java截取(提取)子字符串(substring()),Java分割字符串(split())
在 String 中提供了两个截取字符串的方法,一个是从指定位置截取到字符串结尾,另一个是截取指定范围的内容。下面对这两种方法分别进行介绍。 1. substring(int beginIndex) 形式 此方式用于提取从索引位置开始至结尾处的字符串部分。调用时,…...
从厨房间到股市:家庭主妇的华美转身
我一直是一个安于现状的家庭主妇。生活中,我热爱烹饪、园艺和照顾家人,但我也渴望能有更多的自我实现和价值感。在机缘巧合下,我接触到了卓扬网,一个专业的股票投资平台。从那刻起,我的人生发生了翻天覆地的变化。 初…...

Oracle 数据库的锁排查方法
关键字 oracle lock 问题描述 Oracle 数据库上锁问题如何排查 解决问题思路 准备数据 create table lock_test(name varchar(10),age varchar(10));insert into lock_test values(ff,10); insert into lock_test values(yy,20); insert into lock_test values(ll,30);Orac…...
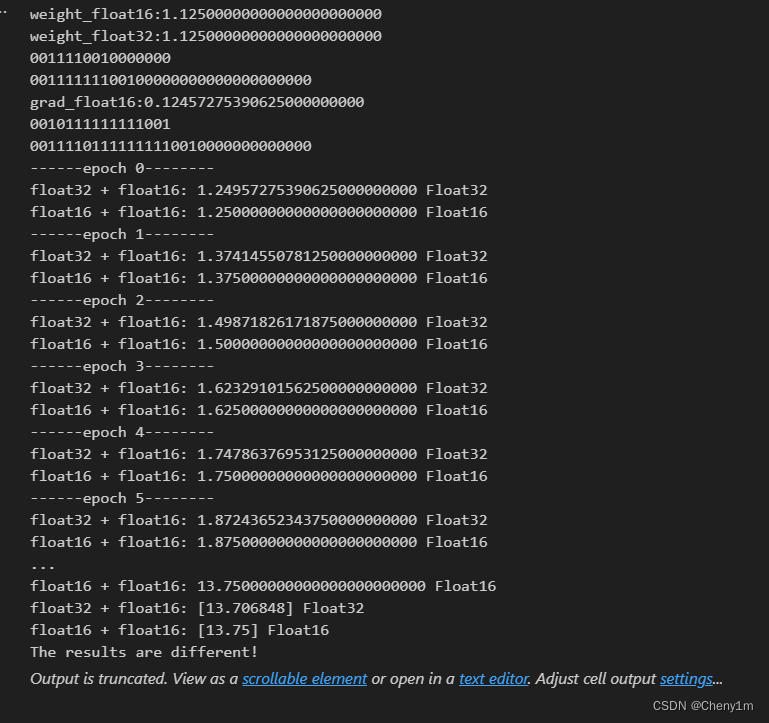
混合精度训练原理之float16和float32数据之间的互相转换
混合精度训练原理之float16和float32数据之间的互相转换 本篇文章参考:全网最全-混合精度训练原理 上述文章已经讲解的比较详细,本文只是从数值角度分析: 1. float32转入float16的精度误差 2. 在深度学习的混精度训练当中,当参数…...
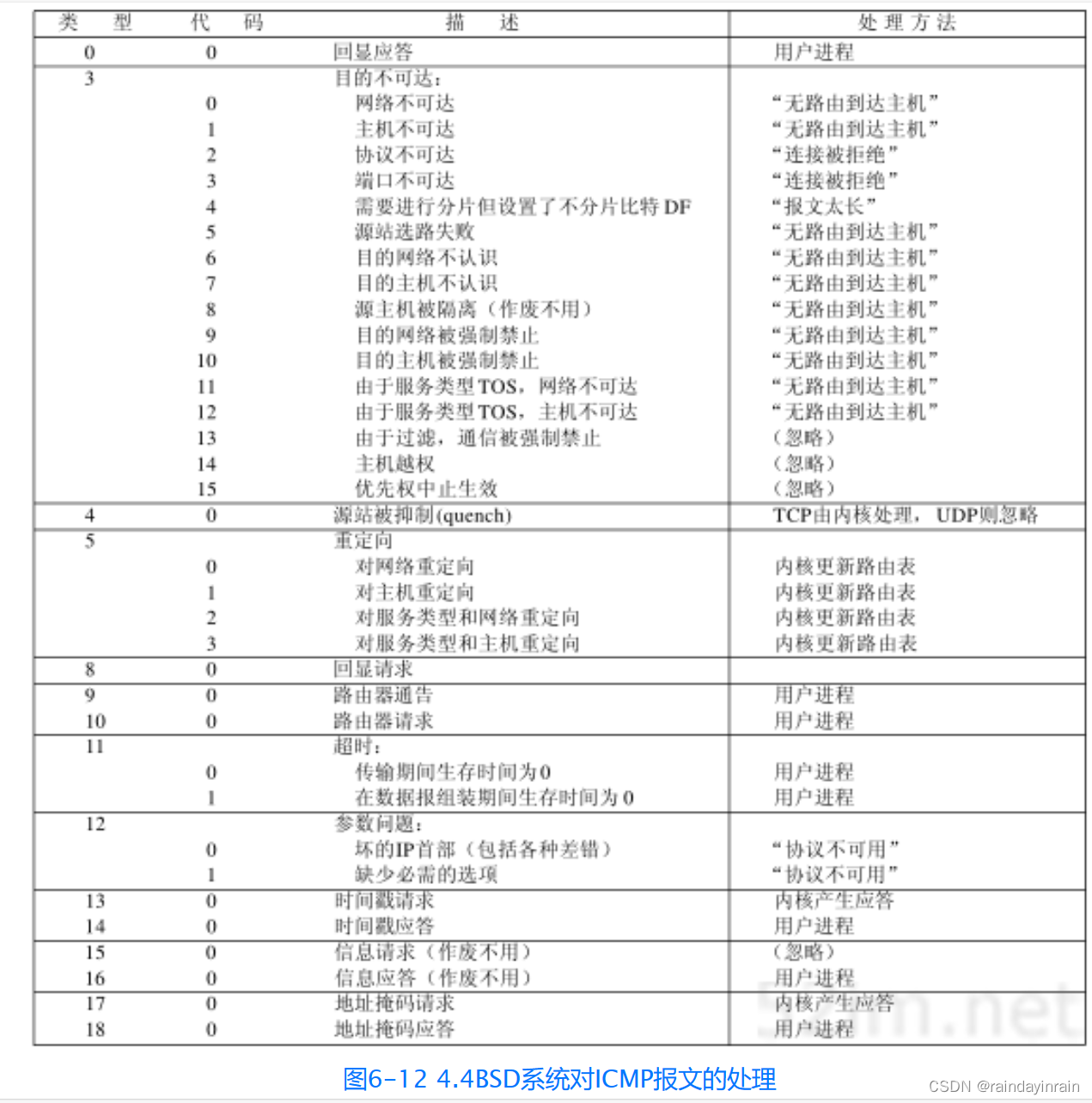
网络协议--ICMP:Internet控制报文协议
6.1 引言 ICMP经常被认为是IP层的一个组成部分。它传递差错报文以及其他需要注意的信息。ICMP报文通常被IP层或更高层协议(TCP或UDP)使用。一些ICMP报文把差错报文返回给用户进程。 ICMP报文是在IP数据报内部被传输的,如图6-1所示。 ICMP…...
《红蓝攻防对抗实战》三.内网探测协议出网之HTTP/HTTPS协议探测出网
目录 一. 在 Windows 操作系统中探测 HTTP/HTTPS 出网 1. Bitsadmin 命令 2.Certuil 命令 2.Linux系统探测HTTP/HTTPS出网 1.Curl命令 2.Wget命令 对目标服务器探测 HTTP/HTTPS 是否出网时,要根据目标系统类型执行命令,不同类型的操作系统使用的探…...
【Win11】系统重装教程(最新最详细)
目录 一.简介 二.用U盘制作PE系统 三、安装系统 软件:Windows 11版本:21H2语言:简体中文大小:5.14G安装环境:PE系统,至少7代处理器硬件要求:CPU2.0GHz 内存4G(或更高)下载通道①丨…...
如何构建一个外卖微信小程序
随着外卖行业的不断发展,越来越多的商家开始关注外卖微信小程序的开发。微信小程序具有使用方便、快速上线、用户覆盖广等优势,成为了商家们的首选。 那么,如何快速开发一个外卖微信小程序呢?下面就让我们来看看吧! 首…...
小知识(5) el-table行样式失效问题
一、实现效果 子级呈现不同颜色去区分 二、最初代码 tips: 我这里使用的vue3 elementplus <el-table :row-class-name"tableRowClassName" >... </el-table>function tableRowClassName({ row, rowIndex }) {if (row.children.length 0) {return …...
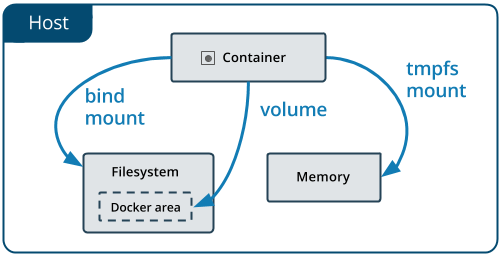
【Docker】Docker数据的存储
默认情况下,在运行中的容器里创建的文件,被保存在一个可写的容器层里,如果容器被删除了,则对应的数据也随之删除了。 这个可写的容器层是和特定的容器绑定的,也就是这些数据无法方便的和其它容器共享。 Docker主要提…...

hive字段关键字问题处理
最近在xxl_job部署shell调度任务时,发现在编写Hql时,对一些使用关键字命名的字段无法解析,按开发规范,字段命名不应该有关键字,但是数据来源是第三方,无法修改,需要通过flume对从kafka的数据到hdfs上,数据是json格式,所以需要对关…...

指定顺序输出
系列文章目录 进阶的卡莎C++_睡觉觉觉得的博客-CSDN博客数1的个数_睡觉觉觉得的博客-CSDN博客双精度浮点数的输入输出_睡觉觉觉得的博客-CSDN博客足球联赛积分_睡觉觉觉得的博客-CSDN博客大减价(一级)_睡觉觉觉得的博客-CSDN博客小写字母的判断_睡觉觉觉得的博客-CSDN博客纸币(…...
(Java)中的数据类型和变量
文章目录 一、字面常量二、数据类型三、变量1.变量的概念2.语法的格式3.整型变量4.长整型变量5.短整型变量6.字节型变量 四、浮点型变量1.双精度浮点数2.单精度浮点数 五、字符型常量六、布尔型变量七、类型转换1.自动类型转换(隐式)2.强制类型转换(显式…...
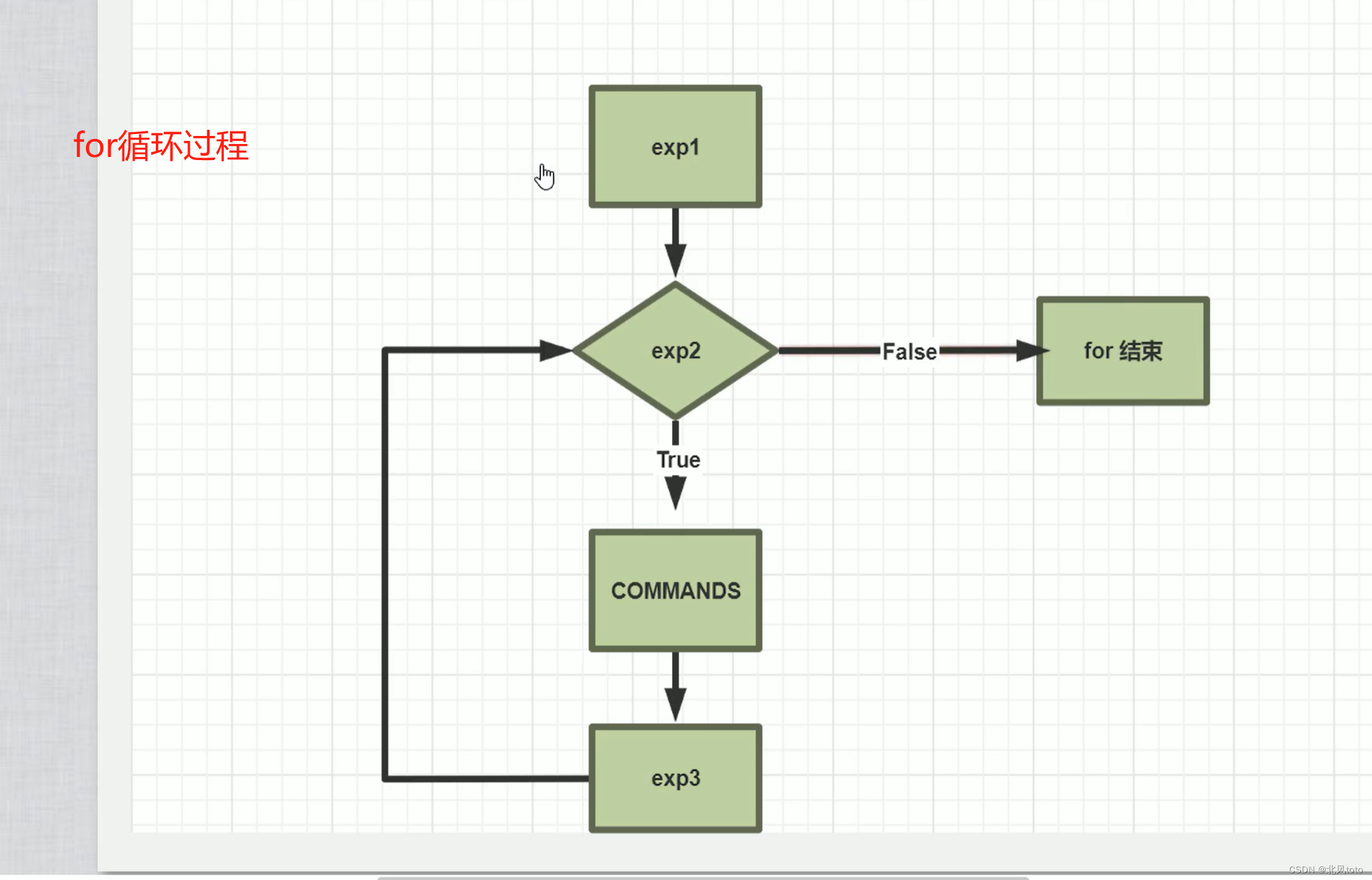
SHELL脚本编程基础,bilibili王晓春老师课程个人笔记(写比较简单,仅供参考)
文章目录 一、第一天(Shell脚本编程基础)作者视频ppt部分作者视频操作编写一个hello.sh可执行文件使hello.sh可以到处运行没有执行权限的执行方式下载httpd(web服务器)curl字符界面浏览器 命令列表凌乱笔记 作业重点: …...

VS code运行vue项目
要在VS Code中启动Vue项目,您可以按照以下步骤进行操作: 1.打开VS Code,并确保已安装Vue.js插件(如Vetur)。 2.在VS Code的侧边栏中,选择您的Vue项目文件夹,或者使用菜单中的“文件”->“打…...
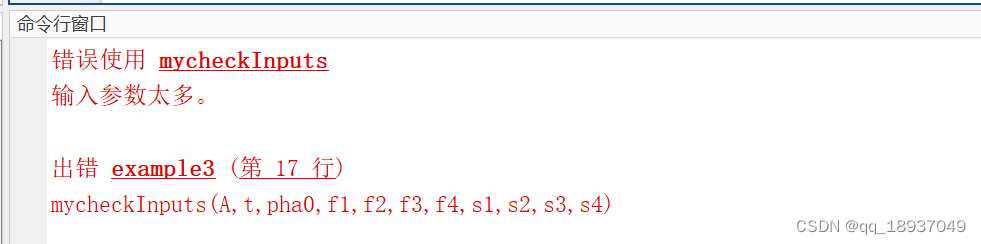
matlab中narginchk函数用法及其举例
matlab中narginchk函数用法及其举例 narginchk在编写子函数程序时候,在验证输入参数数目方面具有重要作用,本博文讲一讲该函数的用法。 一、narginchk功能 narginchk的作用是验证输入参数数目。 二、语法 narginchk(minArgs,maxArgs)narginchk(minA…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
