【蓝桥】小蓝的疑问
1、题目
问题描述
小蓝和小桥上完课后,小桥回顾了课上教的树形数据结构,他在地上画了一棵根节点为 1 的树,并且对每个节点都赋上了一个权值 w i w_i wi。
小蓝对小桥多次询问,每次询问包含两个整数 x , k x,k x,k,表示询问节点为 x x x 的所有 k k k 层子节点中,最大值是多少。
我们称节点 v v v 为 x x x 的 k k k 层子节点满足:
- v v v 是 x x x 为根的子树中的节点。
- d e p v − d e p x = k dep_v - dep_x = k depv−depx=k, d e p v dep_v depv 为 v v v 在树中的深度。
例如:
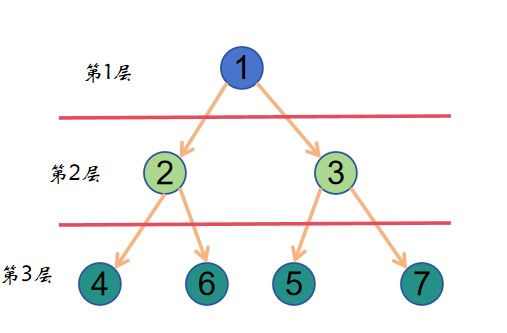
{2, 3} 为 1 号点的 1 层子节点,{4, 5, 6, 7} 为 1 号点的 2 层子节点,{4, 6} 为 2 号点的 1 层子节点。
输入格式
第一行输入两个正整数 n , q n,q n,q,表示树的节点数量和询问数量。
第二行输入 n n n 个正整数 w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn,表示每个点的权值。
接下来 n − 1 n-1 n−1 行,每行输入两个整数 v i , u i v_i, u_i vi,ui,表示存在一条由 v i v_i vi 指向 u i u_i ui 的边。
接下来 q q q 行,每行输入两个整数 x , k x, k x,k,表示询问 x x x 的 k k k 层子节点中,最大值是多少。
输出格式
输出 q q q 行,每行输出一个整数,表示每个询问的最大值。
样例输入
7 4
2 9 8 7 8 6 4
1 2
1 3
2 4
2 6
3 5
3 7
1 2
1 1
3 1
2 1
样例输出
8
9
8
7
说明
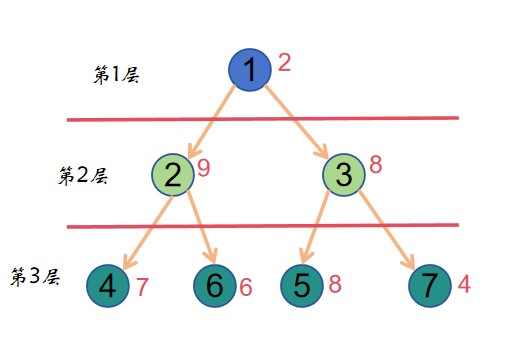
样例如下图:
数据范围
- 1 ≤ v i , u i , k , x ≤ n ≤ 1 0 5 1 \le v_i, u_i, k, x \le n \le 10^5 1≤vi,ui,k,x≤n≤105
- 1 ≤ w i ≤ 1 0 9 1 \le w_i \le 10^9 1≤wi≤109
- 1 ≤ q ≤ 1 0 5 1 \le q \le 10^5 1≤q≤105
- 数据保证是一棵以 1 为根的有向树,并且每次询问的 k k k 一定合法。
原题链接
小蓝的疑问
2、思路
考察数据结构(堆,线段树),图(DFS序),二分查找
- 离线做法:启发式合并 + 优先队列,同时对于每层的节点都维护一个大根堆,每次询问,查询堆中最大值。时间复杂度: O ( n l o g 2 n ) O(n log^2n) O(nlog2n)。
- 在线做法:DFS序 + 线段树(ST表)+ 二分查找,对每层按照 DFS 序相对顺序建立线段树(或者 ST 表),当查询到 u u u 时,通过二分找到 k k k 层的左右端点,查询最大值。时间复杂度: O ( n l o g n ) O(n log n) O(nlogn)。

3、代码
- 强制合并
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>
using namespace std;typedef long long ll;
const int N = 1e5 + 100;
const int MOD = 998244353;vector<int> G[N];
int n, q;
int w[N];
int Siv[N], Son[N], ans[N];typedef pair<int, int> Pair;vector<Pair> query[N];priority_queue<Pair> Dep[N];int DFN = 0, rdn[N], dfn[N], dep[N];
int vis[N];int ddep[N];void dfs(int u, int fa = 0, int dpt = 1) {ddep[u] = dpt;Siv[u] = 1;for (int v : G[u]) {if (v == fa) continue;dfs(v, u, dpt + 1);ddep[u] = max(ddep[u], ddep[v]);Siv[u] += Siv[v];if (Siv[v] > Siv[Son[u]]) Son[u] = v;}
}void to_get_ans(int u, int fa = 0, int dpt = 1, bool clr = false) {dfn[u] = ++DFN;rdn[dfn[u]] = u;dep[u] = dpt;for (int v : G[u]) {if (v == fa || v == Son[u]) continue;to_get_ans(v, u, dpt + 1, false);}if (Son[u]) {to_get_ans(Son[u], u, dpt + 1, true);}int ed = dfn[u];if (Son[u]) ed = dfn[Son[u]] - 1;for (int i = dfn[u]; i <= ed; ++i) {int vv = rdn[i];Dep[dep[vv]].push({w[vv], vv});vis[vv] = true;}// cout << endl;for (Pair q : query[u]) {int k = q.first;assert(k + dpt <= ddep[u]);int id = q.second;while (Dep[k + dpt].size() && vis[Dep[k + dpt].top().second] == 0) {Dep[k + dpt].pop();}ans[id] = Dep[k + dpt].top().first;}if (!clr) {int ed = dfn[u] + Siv[u];for (int i = dfn[u]; i < ed; ++i) {vis[rdn[i]] = false;}}}void sol() {cin >> n >> q;for (int i = 1; i <= n; ++i) {cin >> w[i];} int u, v; for (int i = 1; i < n; ++i) {cin >> u >> v;G[u].push_back(v);G[v].push_back(u);}dfs(1);int x, k;for (int i = 1; i <= q; ++i) {cin >> x >> k;query[x].push_back({k, i});}to_get_ans(1);for (int i = 1; i <= q; ++i) {cout << ans[i] << '\n';}
}int main() {int T = 1;while (T--) {sol();}exit(0);
}
- 面向对象
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>
#include <cmath>using namespace std;typedef long long ll;
const int N = 1e5 + 100;vector<int> G[N], val[N], dfsQ[N];
int w[N], n, q;
int DFN = 0, dfn[N], dep[N], Siv[N], MaxDpt = 0;class RMQ_t {
public:RMQ_t(const vector<int>& init);~RMQ_t();int query(int l, int r) const {int k = log2(r - l);return max(f[k][l], f[k][r - (1 << k)]);}
private:int **f;const int N, LOGN;
};RMQ_t *res[N];void dfs(int u, int fa = 0, int dpt = 1) {MaxDpt = max(MaxDpt, dpt);dfn[u] = ++DFN; dep[u] = dpt;Siv[u] = 1;val[dpt].push_back(w[u]);dfsQ[dpt].push_back(dfn[u]);for (int v : G[u]) {if (v == fa) continue;dfs(v, u, dpt + 1);Siv[u] += Siv[v];}
}void sol() {cin >> n >> q;for (int i = 1; i <= n; ++i) {cin >> w[i];} int u, v, x, k; for (int i = 1; i < n; ++i) {cin >> u >> v;G[u].push_back(v);G[v].push_back(u);}dfs(1);for (int i = 1; i <= MaxDpt; ++i) {res[i] = new RMQ_t(val[i]);}while (q--) {cin >> x >> k;int l = lower_bound(dfsQ[k + dep[x]].begin(),dfsQ[k + dep[x]].end(),dfn[x]) - dfsQ[k + dep[x]].begin();int r = lower_bound(dfsQ[k + dep[x]].begin(),dfsQ[k + dep[x]].end(),dfn[x] + Siv[x]) - dfsQ[k + dep[x]].begin();cout << res[k + dep[x]]->query(l,r) << endl;}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T = 1;while (T--) {sol();}exit(0);
}RMQ_t::RMQ_t(const vector<int>& init) : N(init.size()), LOGN(log2(init.size()) + 1) {f = new int*[LOGN];for (int i = 0; i < LOGN; ++i) {f[i] = new int[N];}for (int i = 0; i < N; ++i) {f[0][i] = init[i];}for (int i = 1; i < LOGN; ++i) {for (int j = 0; j + (1 << i) - 1 < N; ++j) {f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);}}
}RMQ_t::~RMQ_t() {for (int i = 0; i < LOGN; ++i) {delete[] f[i];}delete[] f;
}
相关文章:

【蓝桥】小蓝的疑问
1、题目 问题描述 小蓝和小桥上完课后,小桥回顾了课上教的树形数据结构,他在地上画了一棵根节点为 1 的树,并且对每个节点都赋上了一个权值 w i w_i wi。 小蓝对小桥多次询问,每次询问包含两个整数 x , k x,k x,kÿ…...
漏洞复现-海康威视综合安防管理平台信息泄露【附Poc】
目录 【产品介绍】 【产品系统UI】 【漏洞说明】 【指纹】 【Nuclei Poc】 【验证】 【产品介绍】 海康威视(Hikvision)是一家总部位于中国杭州的公司,是全球最大的视频监控产品供应商。除了传统的CCTV摄像机和网络摄像机,海…...

【完美世界】被骂国漫之耻,石昊人设战力全崩,现在真成恋爱世界了
【侵权联系删除】【文/郑尔巴金】 深度爆料,《完美世界》动漫第135集预告片已经更新了,但是网友们对此却是一脸槽点。从预告中可以看出,石昊在和战王战天歌的大战中被打成重伤,最后云曦也被战天歌抓住。在云曦面临生死危机的时候…...

34二叉树-BFS和DFS求树的深度
目录 LeetCode之路——104. 二叉树的最大深度 分析 解法一:广度优先遍历 解法二:深度优先遍历 总结 深度优先搜索 (DFS) 广度优先搜索 (BFS LeetCode之路——104. 二叉树的最大深度 给定一个二叉树 root ,返回其最大深度。 二叉树的…...
Android Glide判断图像资源是否缓存onlyRetrieveFromCache,使用缓存数据,Kotlin
Android Glide判断图像资源是否缓存onlyRetrieveFromCache,使用缓存数据,Kotlin import android.graphics.Bitmap import android.os.Bundle import android.util.Log import android.widget.ImageView import androidx.appcompat.app.AppCompatActivity…...

设计模式之创建型模式
创建型模式与对象的创建有关。 创建型模式抽象了对象实例化的过程,这些设计模式提供了一种在创建对象的同时隐藏创建逻辑的方式,而不是使用 new 运算符直接实例化对象。创建型模式有以下 工厂模式(Factory Method) 意图…...
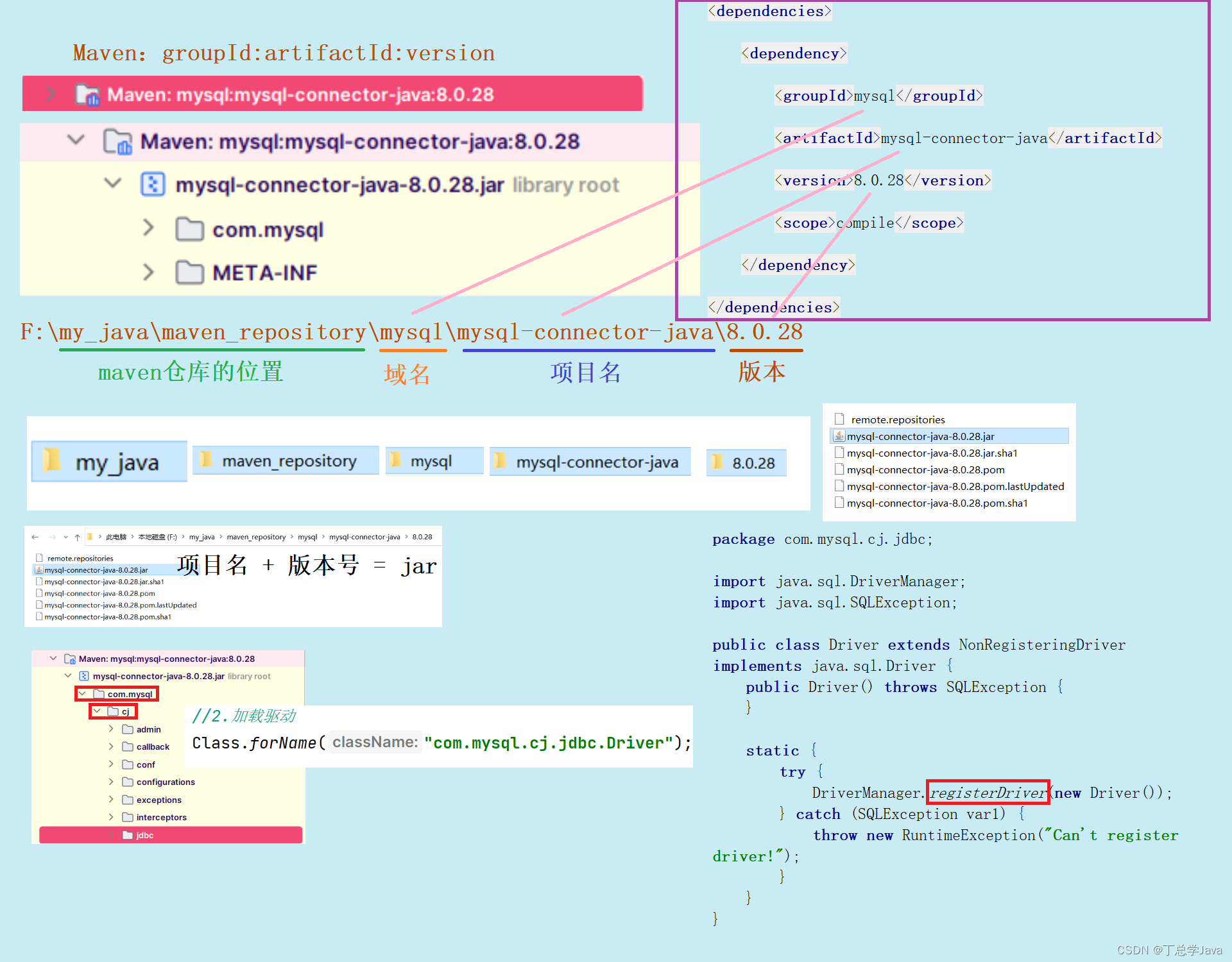
使用jdbc技术连接数据库
连接数据库 <dependencies><dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId><version>8.0.28</version><scope>compile</scope></dependency> </dependencies> g…...

OpenLayers入门,快速搭建vue+OpenLayers地图脚手架项目
专栏目录: OpenLayers入门教程汇总目录 前言 本章针对Vue初学者,对Vue不熟悉,甚至还不会Vue的入门学生读者。 本章会详细讲解从NodeJS环境到npm环境的各个步骤,再到使用vue-cli脚手架快速生成项目,以及添加OpenLayers地图库依赖,编写简单的xyz高德地图显示页面的完整教…...

完成比写得好更重要,先完成初稿再说
我发现自己有个毛病,总想着满意了才动手。于是,经常做到一半跑去看文献,然后陷入文献中觉得这个比自己好,那个比自己好。于是,暂时中断手边工作,最后进度被推迟,甚至啥也没做出来。 今晚再次听…...

Spring boot 处理复杂json接收,同种类型、不同场景处理
场景: json大体格式一致,但是 ext_info 扩展字段对象,场景不同字段不同根据某字段类型,不同值,对应不同实现的 Component,处理不同场景这里根据 event,来做不同处理 {"data": {"event"…...

排列置换环上构造:1025T3
http://cplusoj.com/d/senior/p/SS231025C 排列构造的新知识:上置换环! 我们发现朴素做法是 n 2 n^2 n2 级别的,但数据范围希望我们是 n 2 2 \frac {n^2}2 2n2 级别的。我们发现我们暴力复制序列显得非常蠢,因为很多序列前后…...

Stable diffusion的一些参数意义及常规设置
在线stabel Diffusion模型 https://huggingface.co/spaces/stabilityai/stable-diffusion 随机种子 seed 如果想要同一个文本提示,生成多次都是同一图像,可以设置一个随机种子,类似于random.seed()的原理,并将生成器传递给管道。…...

成员变量、静态成员变量、局部变量、常量的内存区域
一、Java中没有全局变量的概念,变量分为类的成员变量、静态成员变量和方法中的局部变量 1、局部变量,基本类型的局部变量变量名和值都存放在虚拟机栈中,引用类型的局部变量变量名存放在栈中,而变量指向的对象存放在堆中。记也很好…...
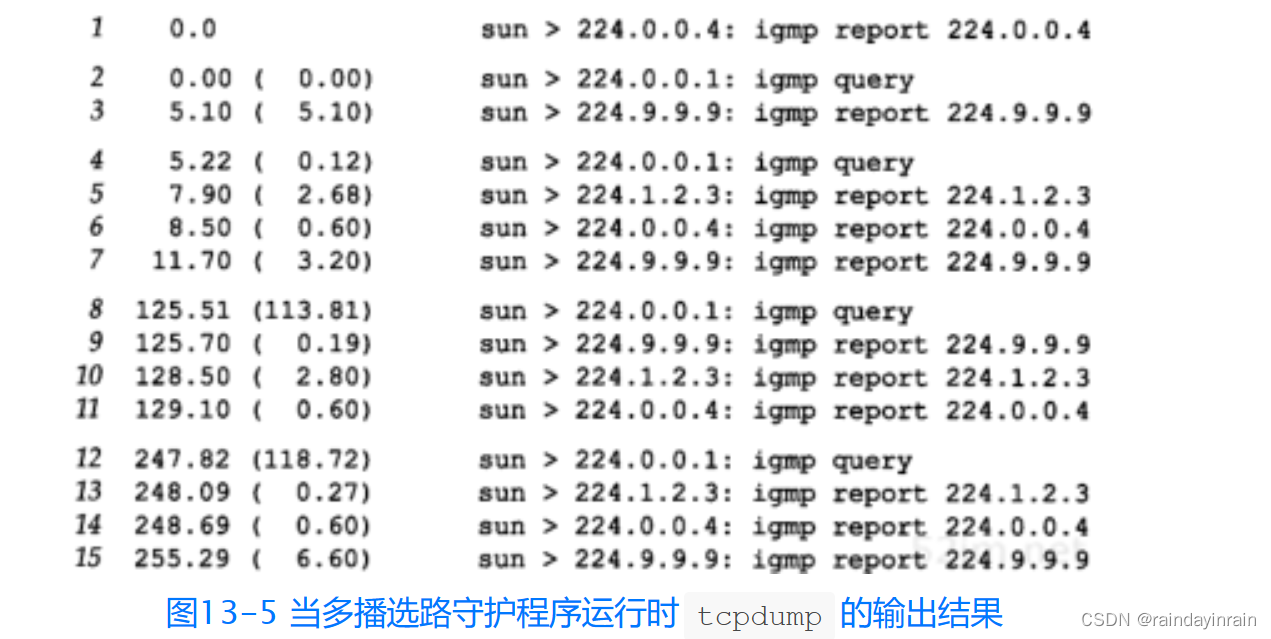
网络协议--IGMP:Internet组管理协议
13.1 引言 12.4节概述了IP多播给出,并介绍了D类IP地址到以太网地址的映射方式。也简要说明了在单个物理网络中的多播过程,但当涉及多个网络并且多播数据必须通过路由器转发时,情况会复杂得多。 本章将介绍用于支持主机和路由器进行多播的In…...
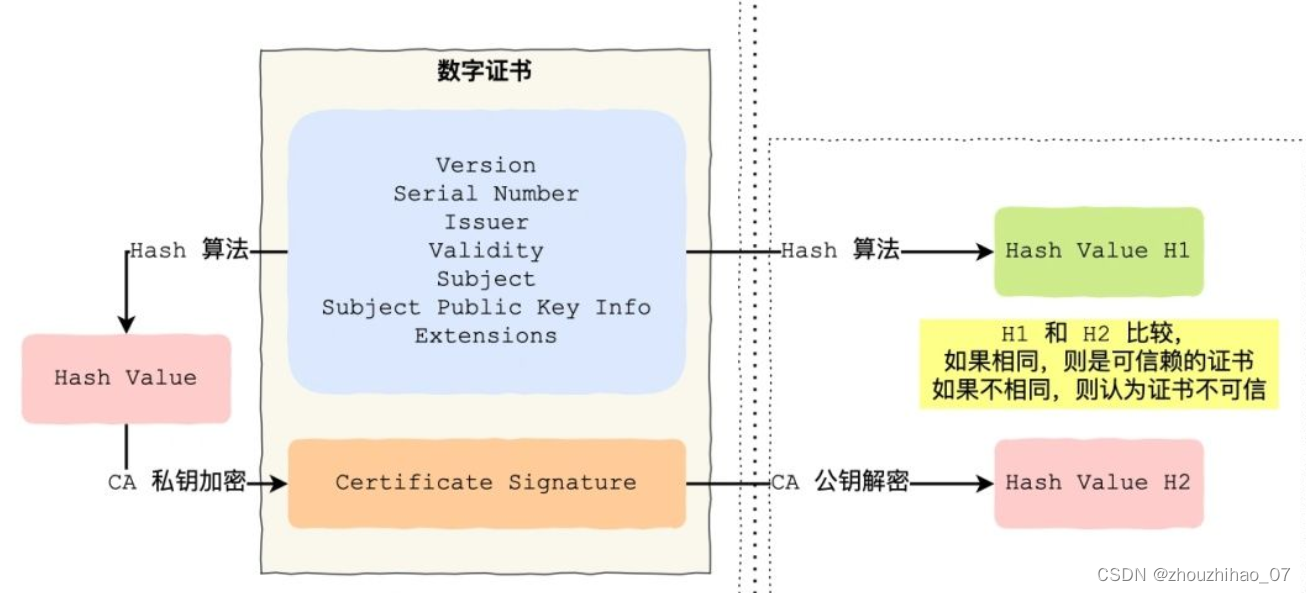
网络安全https
http是明文的,相当于在网上裸奔,引出了https,大多数网站都转为了https,连非法的赌博网站有的都是https的。 1.https的网站是不是必须让用户装数字证书? 答:分两种,一种是单向认证,像…...

xcode Simulator 手动安装
xcode Simulator 手动安装 参考文档 xcode又又又升级了,升级完成之后不下载最新的 iOS 17 Simulator就不能编译运行了,只能静静的等他下载。但是离谱的是这个居然没有断点续下,每次都要重新下载,眼睁睁的看着下载了4个G然后断掉…...

Unity中国、Cocos为OpenHarmony游戏生态插上腾飞的翅膀
2023年是OpenHarmony游戏生态百花齐放的一年!为了扩展OpenHarmony游戏生态,OpenHarmony在基金会成立了游戏SIG小组,游戏SIG小组联合cocos,从cocos2dx入手一周内快速适配了cocos2.2.6的MVP版本,随后又分别适配了cocos2d…...

Monaco Editor编辑器
monaco-editor Monaco Editor 是一个基于浏览器的代码编辑器,由微软开发。它提供了丰富的功能,包括语法高亮、智能代码补全、代码折叠、多光标编辑等。Monaco Editor 是 Visual Studio Code 的核心编辑器,也被广泛用于其他开发工具和在线代码…...

ARM | 传感器必要总线IIC
IIC总线介绍 1.谈谈你对IIC总线理解? 1)IIC总线是串行半双工同步总线,主要用于连接整体电路 2)SCL/SDA作用:IIC是两线制,一根是时钟线SCK,用于控制什么时候进行进行数据传输,时钟信号由主机发出; 另一根是数据线SDA,用于进行数据传输,可以从…...
Mybatis中Resources和ClassLoaderWrapper
ClassLoaderWrapper Resources...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
