线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
相关文章
- K近邻算法和KD树详细介绍及其原理详解
- 朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解
- 决策树算法和CART决策树算法详细介绍及其原理详解
- 线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
文章目录
- 相关文章
- 前言
- 一、线性回归
- 二、逻辑斯谛回归
- 总结
前言
今天给大家带来的主要内容包括:线性回归算法、逻辑斯谛回归算法。废话不多说,下面就是本文的全部内容了!
一、线性回归
假设小明现在有一个游戏战队,我们称其为蓝色战队,这支战队队员的游戏手感都比较慢热,在整个游戏比赛期间不同阶段的两个战队的得分情况如下所示:

- 第5min:蓝色战队和橙色战队零十开
- 第10min:蓝色战队和橙色战队一九开
- 第20min:蓝色战队和橙色战队五五开
- 第35min:蓝色战队和橙色战队九一开
- 第40min:蓝色战队和橙色战队十零开
由于游戏赛场上的情况变化莫测,作为游戏战队老板的小明想知道在比赛的第26min的时候,蓝色战队和橙色战队几几开呢?或者在比赛的其他时间,蓝色战队和橙色战队又是几几开呢?如果可以得到这样的数据,就可以帮助小明发掘他战队队员的最大潜力了。

为了得到以上信息,我们需要进行计算,在进行计算之前,首先我们要明确,几几开就代表着事情发生的几率,也就是蓝色战队赢下对局和输掉对局可能性的比值。我们把这些几率值列出来:

为了方便观察,我们把它转化为小数:

根据以上计算结果可以发现,当队伍十分可能输给对面的时候,赢的几率接近于零;当战队非常可能赢的时候,赢得几率接近于正无穷:

虽然我们现在可以得到不同比赛时间的蓝色队伍获胜的概率分布情况,但是这种在正半轴十分不对称的分布不太好分析问题,所以我们使用几率的对数来分析数据:

可以看到,这样就可以把数据从正半轴重新映射回整条数轴上了:

如果我们以对数几率作为yyy轴,比赛时间作为xxx轴,就可以把所有比赛的数据映射到x⋅yx \cdot yx⋅y平面上了:

可以发现,上图就是我们耳熟能详的线性回归。我们都知道,通过每一个点到直线的距离差,然后做一个最小二乘法的优化:
e(w,b)=12∑i=1N∣∣ei∣∣2e(w,b)=\frac{1}{2}\sum_{i=1}^{N}||e_{i}||^{2} e(w,b)=21i=1∑N∣∣ei∣∣2
利用上式进行最小二乘法的优化后,就可以得到一条最完美的直线来拟合这些数据,得到这条直线之后,我们只需要查询xxx轴所对应的时间,就可以求出赢下这场比赛的可能性了:

以上就是对于线性回归的介绍。
二、逻辑斯谛回归
虽然看起来我们可以得到比赛中不同时间段的蓝色队伍获胜的可能性,但是其中有许多数据点的yyy值是正负无穷,这种情况可是没有办法计算数据和直线的距离误差的:

为了解决这个问题,我们可以考虑把这条直线重新映射回概率空间,我们是以对数几率作为yyy轴的,所以yyy的值为:
y=log(p1−p)y = \log(\frac{p}{1-p}) y=log(1−pp)
我们现在要把概率ppp写成yyy的函数,所以等式两边做一个自然对数的幂:
ey=p1−pe^{y}=\frac{p}{1-p} ey=1−pp
然后等式两边同时乘以1−p1-p1−p:
(1−p)ey=p(1-p)e^{y}=p (1−p)ey=p
把括号展开:
ey−pey=pe^{y}-pe^{y}=p ey−pey=p
然后等式两边交换peype^{y}pey:
ey=p+peye^{y}=p+pe^{y} ey=p+pey
这样等式的右面就可以提出公共项ppp:
ey=(1+ey)pe^{y}=(1+e^{y})p ey=(1+ey)p
此时,我们就可以得到ppp的表达式:
p=ey1+eyp=\frac{e^{y}}{1+e^{y}} p=1+eyey
上式就是逻辑斯谛函数,当我们把直线y=wx+by=wx+by=wx+b的表达式代入到公式中,就得到了概率空间的表达:
p=ewx+b1+ewx+bp=\frac{e^{wx+b}}{1+e^{wx+b}} p=1+ewx+bewx+b
上式就是逻辑斯谛回归的概率函数,因此,我们可以这样理解,概率空间内的逻辑斯谛回归,其实就是对数几率空间内的线性回归:

此时,我们已经可以在概率空间中讨论不同比赛时间的蓝色队伍获胜的可能性了:

既然回到了概率空间,我们就可以使用概率论中的极大似然估计,来得到拟合情况最好的逻辑斯谛曲线。首先,我们假设对于在时间xxx时蓝色队伍赢下比赛的概率为ppp:
p(y=1∣x)=pp(y=1|x)=p p(y=1∣x)=p
那么蓝色队伍在时间xxx时输掉比赛的概率就是1−p1-p1−p:
p(y=0∣x)=1−pp(y=0|x)=1-p p(y=0∣x)=1−p
因为yyy的值只能取零或一,所以我们可以按照下式来表达任意样本xix_{i}xi的概率:
p(y=?∣xi)=piyi(1−pi)1−yip(y=?|x_{i})=p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}} p(y=?∣xi)=piyi(1−pi)1−yi
使用最大似然估计法得到的似然值就是这些样本概率的乘积:
L=∏i=1Np(y=?∣xi)L=\prod_{i=1}^{N}p(y=?|x_{i}) L=i=1∏Np(y=?∣xi)
我们可以把p(y=?∣xi)=piyi(1−pi)1−yip(y=?|x_{i})=p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}}p(y=?∣xi)=piyi(1−pi)1−yi代入到上式中:
L=∏i=1Npiyi(1−pi)1−yiL=\prod_{i=1}^{N}p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}} L=i=1∏Npiyi(1−pi)1−yi
一系列式子的乘积是一个不太容易优化的表达,所以我们取它的对数形式,把乘法转化为加法:
log(L)=∑i=1Nyilog(pi)+(1−yi)log(1−pi)\log (L)=\sum_{i=1}^{N} y_{i} \log \left(p_{i}\right)+\left(1-y_{i}\right) \log \left(1-p_{i}\right) log(L)=i=1∑Nyilog(pi)+(1−yi)log(1−pi)
然后把括号展开整理一下:
log(L)=∑i=1Nyilogpi1−pi+log(1−pi)\log (L)=\sum_{i=1}^{N} y_{i} \log \frac{p_{i}}{1-p_{i}}+\log \left(1-p_{i}\right) log(L)=i=1∑Nyilog1−pipi+log(1−pi)
可以看到,在上式中,等号右面的式子中出现了logpi1−pi\log \frac{p_{i}}{1-p_{i}}log1−pipi这个熟悉的身影,这就是之前我们介绍的对数几率,因为逻辑斯谛回归就是对数几率空间内的线性回归,所以我们可以将logpi1−pi\log \frac{p_{i}}{1-p_{i}}log1−pipi替换成直线的方程:
log(L)=∑i=1Nyi(wxi+b)+log(1−pi)\log (L)=\sum_{i=1}^{N} y_{i} (wx_{i}+b)+\log \left(1-p_{i}\right) log(L)=i=1∑Nyi(wxi+b)+log(1−pi)
需要注意的是,上式最后面的pip_{i}pi值就是逻辑斯谛函数,所以我们将逻辑斯谛函数pi=ewxi+b1+ewxi+bp_{i}=\frac{e^{wx_{i}+b}}{1+e^{wx_{i}+b}}pi=1+ewxi+bewxi+b代入上式即可:
log(L)=∑i=1Nyi(wxi+b)−log(1+ewxi+b)\log (L)=\sum_{i=1}^{N} y_{i} (wx_{i}+b)-\log \left(1+e^{wx_{i}+b}\right) log(L)=i=1∑Nyi(wxi+b)−log(1+ewxi+b)
上式就是我们最终得到的式子,这个式子之和www和bbb这两个参数相关,我们可以使用最大似然估计优化方法得到最好的www和bbb这两个参数:
w^,b^=argmaxw,b∑i=1Nyi(wxi+b)−log(1+ewxi+b)\widehat{w}, \widehat{b}=argmax_{w,b}\sum_{i=1}^{N}y_{i}(wx_{i}+b)-\log(1+e^{wx_{i}+b}) w,b=argmaxw,bi=1∑Nyi(wxi+b)−log(1+ewxi+b)
当我们得到最优的参数www和bbb的值后,就可以将x=26x=26x=26代入:
p(26)=ew^×26+b^1+ew^×26+b^p(26)=\frac{e^{\widehat{w}\times 26+ \widehat{b}}}{1+e^{\widehat{w}\times 26+ \widehat{b}}} p(26)=1+ew×26+bew×26+b
这样就可以得到在比赛的第26分钟时,蓝色战队获胜的概率了:

以上就是逻辑斯谛回归的全部过程。
总结
以上就是本文的全部内容了,这个系列还会继续更新,给大家带来更多的关于机器学习方面的算法和知识,下篇博客见!
相关文章:

线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解 文章目录相关文章前言一、线性回归二、逻辑斯谛回归总结前言 今天给大家…...

【网络原理8】HTTP请求篇
在上一篇文章当中,我们也提到了什么是HTTP。 每一个HTTP请求,都会对应一个HTTP响应。 下面这一篇文章,将聊一下HTTP请求的一些内容 目录 一、URL 第一部分:协议名称 第二部分:认证信息(新的版本已经没有了) 第三部分…...
Playbook的用法
目录 Playbook Playbook 与 Ad-Hoc 对比 YAML 语言特性 YAML语法简介 支持的数据类型 写法格式 1 scalar 标量 建议缩进两个空格,可多 2 Dictionary 字典 3 List 列表 三种常见的数据格式 Playbook 核心组件 不要用 tab 可以#注释 hosts remote_us…...
APP优化 —— MMAP内存映射
mmap 一种内存映射文件的方法 mmap将一个文件或者其它对象映射进内存。文件被映射到多个页上,如果文件的大小不是所有页的大小之和,最后一个页不被使用的空间将会清零。mmap在用户空间映射调用系统中作用很大。 头文件 <sys/mman.h> 函数原型 v…...

paddle.vision 与 torchvision 中的box NMS使用方式
torchvision 中有多个用于计算 BBox NMS 的 API, 在本篇氵文中, 使用 torchvision.ops.boxes.batched_nmspaddle.vision 中通过 paddle.vision.ops.nms 来进行多个 Box 的 NMS 操作 1. torchvision 中 batched_nms 操作 torchvision batched_nms def batched_nms(boxes: to…...
php mysql校园帮忙领取快递平台
1、后台管理员用户名hsg 密码hsg 2、开发语言:PHP,数据库为MySql 3、数据库连接字符串在conn.php中修改 4、运行环境wamp5.1.7或者appserv2.5.9 5.程序编码gbk.不支持php5.3以上版本 6.本人发布的程序一律享有免费运行一次…...
C/C++开发,无可避免的内存管理(篇二)-约束好跳脱的内存
一、养成内存管理好习惯 1.1 养成动态对象创建、调用及释放好习惯 开发者手动接管内存分配时,必须处理这两个任务。分配原始内存时,必须在该内存中构造对象;在释放该内存之前,必须保证适当地撤销这些对象。如果你的项目是c项目&am…...
【Java】让我们对多态有深入的了解(九)
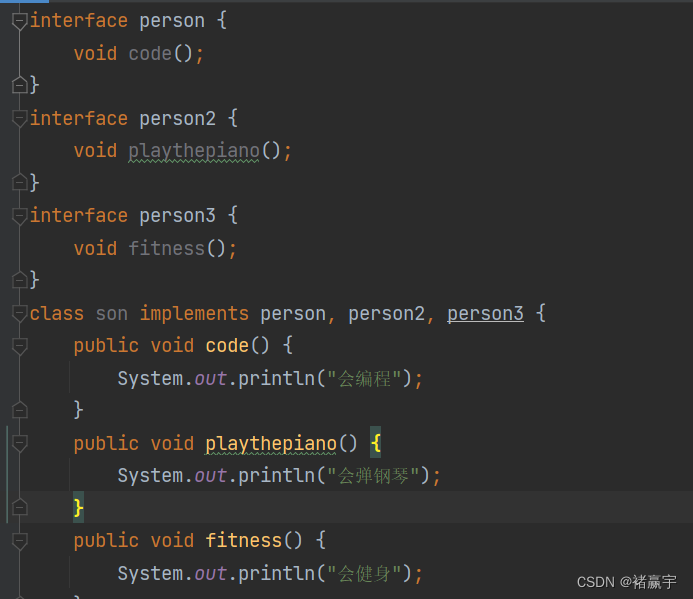
目录 (1)接口的基本介绍编辑 (2)接口的注意事项和细节 1.接口不能被实例化 2.接口中所有方法是public方法,接口中的抽象方法,可以不用abstract修饰 3.一个普通类实现接口,必须将接口所有…...
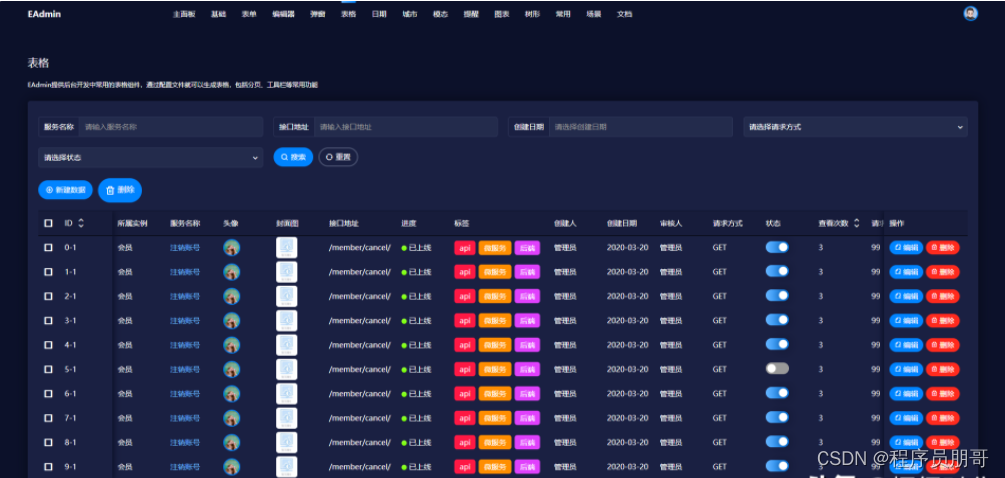
12 个适合做外包项目的开源后台管理系统
1.D2admin 开源地址:https://github.com/d2-projects/d2-admin 文档地址:https://d2.pub/zh/doc/d2-admin/ 效果预览:https://d2.pub/d2-admin/preview/#/index 开源协议:MIT 2.vue-element-admin 开源地址:https…...
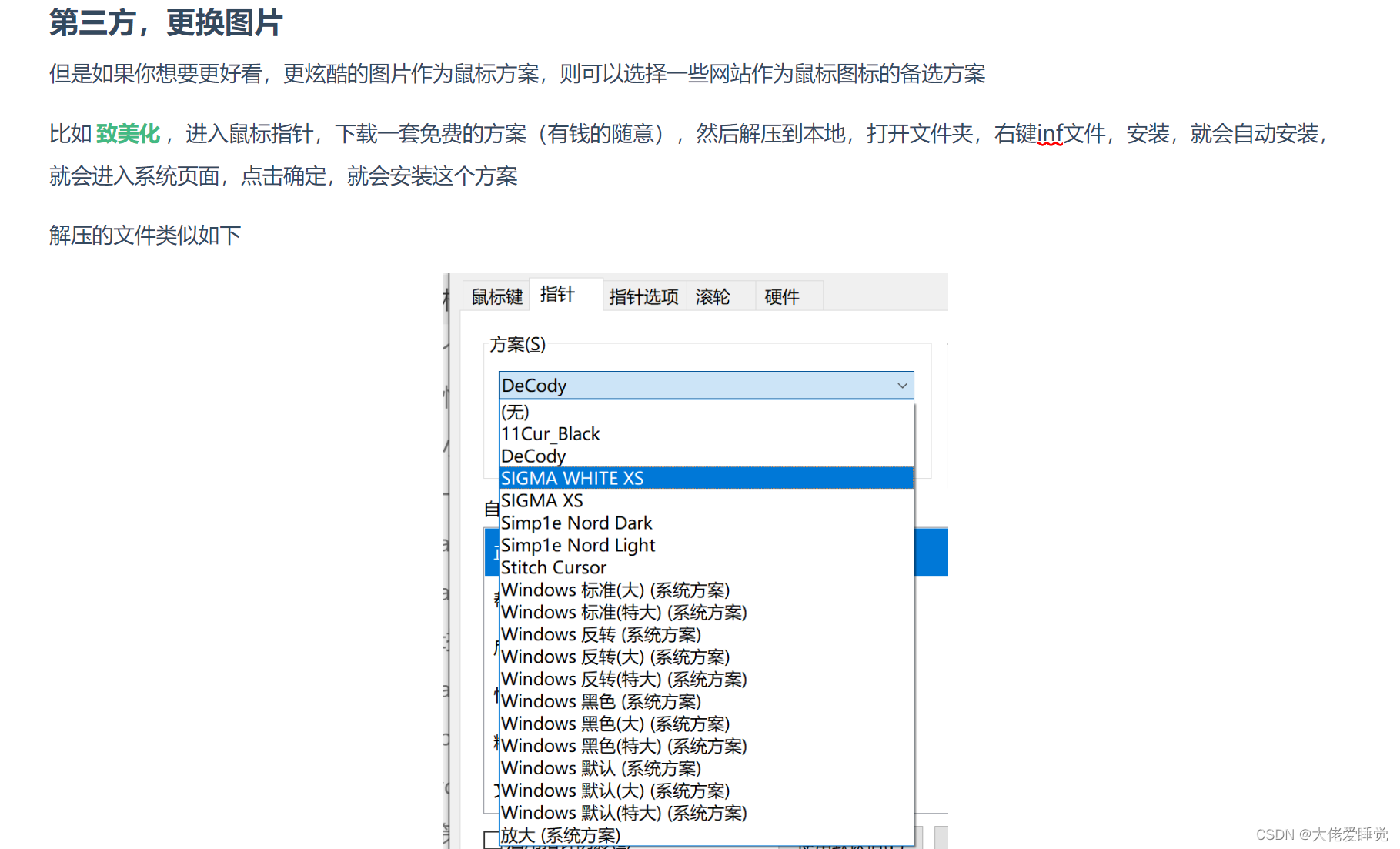
鼠标更换指针图案和更改typora的主题
鼠标更换指针图案 由此偶然看见好几个朋友都使用了新的图案替换掉了原有的鼠标图案,今天寻思自己也换一个图案 主要是觉得鼠标大一点儿会好看一些,所以就找了一些教程 官方教程,小的变动 当然最多的是官方教程,如果你只是想要…...
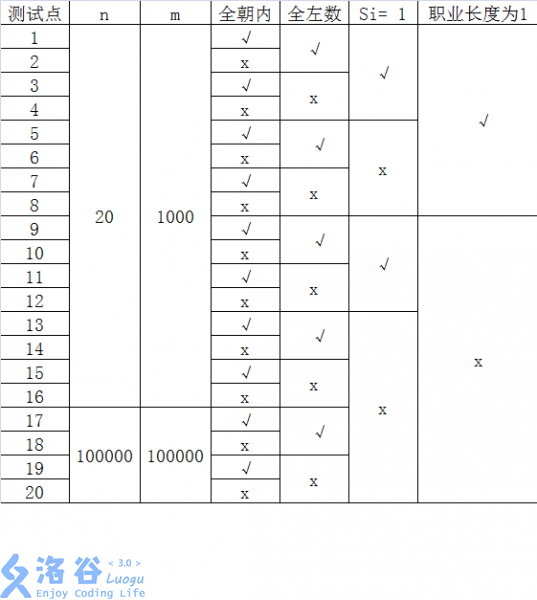
【洛谷 P1563】[NOIP2016 提高组] 玩具谜题(模拟+结构体数组+指针)
[NOIP2016 提高组] 玩具谜题 题目背景 NOIP2016 提高组 D1T1 题目描述 小南有一套可爱的玩具小人, 它们各有不同的职业。 有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图: 这时 singer 告诉小南一个谜…...
阿里测试经验7年,从功能测试到自动化测试,我整理的超全学习指南
做测试七年多,有不少人问过我下面问题: 现在的手工测试真的不行了吗? 测试工程师,三年多快四年的经验,入门自动化测试需要多久? 自学自动化测试到底需要学哪些东西? 不得不说,随着…...
)
Educational Codeforces Round 143 (Rated for Div. 2)
Educational Codeforces Round 143 (Rated for Div. 2) D. Triangle Coloring 思路: 每个环都需要取最大值,那么我们讨论一个环获得最大值选的两条边的可能取法: 显然:如果三边相等,这个环有3种取法。如…...

业务代码编写过程中如何「优雅的」配置隔离
思考 不同的处理方式 1.常规的处理方式,通过某种规则判断区分代码环境 // 获取环境标识 const env getCurrentEnv();if (env dev) {// do something } else if (env test) {// do something } else if (env prod) {// do something } 分析: 1.此种…...

English Learning - L2-2 英音地道语音语调 2023.02.23 周四
English Learning - L2-2 英音地道语音语调 2023.02.23 周四查音标的工具怎么练习效果好准备工作大小声练习大元音开口度的对比舌位对比复习后元音 /ɑː/ /ɔː/ /uː//ɑː//ɔː//uː/前元音 /iː/发音技巧对应单词的发音对应句子的发音常见的字母组合中元音 /ɜː/发音技巧…...
和notify())
java:线程等待与唤醒 - Object的wait()和notify()
java:线程等待与唤醒 - Object的wait()和notify() 1 前言 java使用Object类的wait()和notify()方法,可以实现线程等待和唤醒(Object类为所有类的父类,即所有类天然具有线程等待和唤醒的方法,一般使用Object类的wait(…...
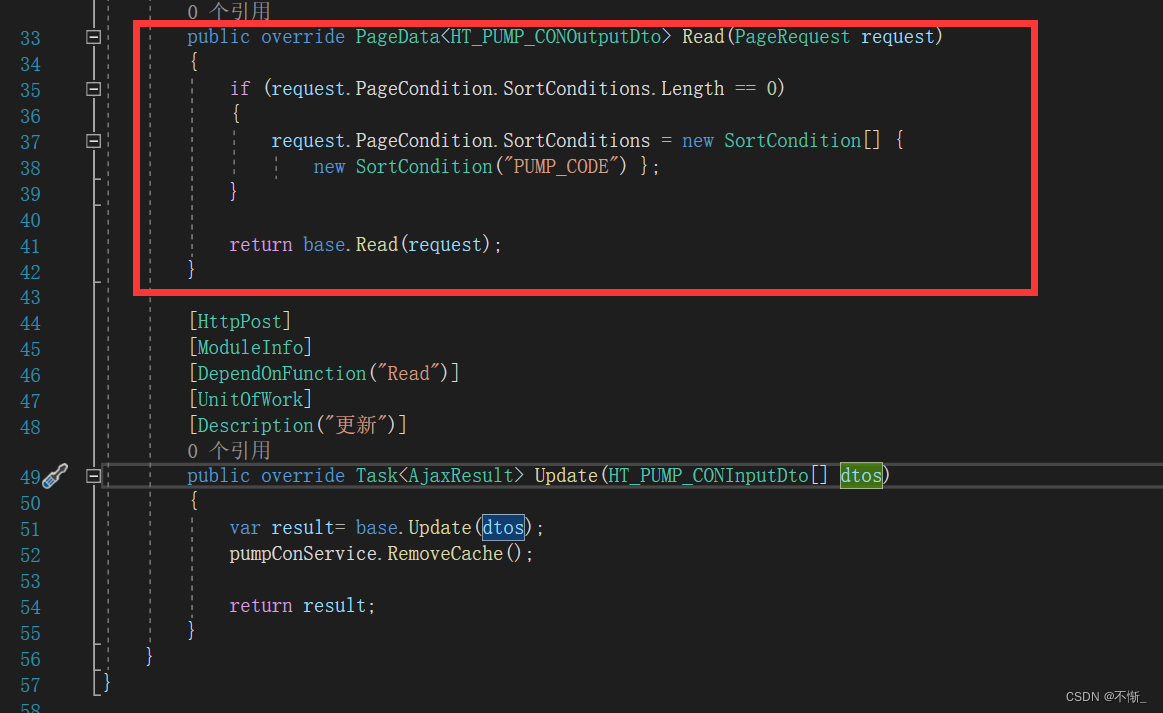
实现弹窗功能并修改其中一个系数
把鼠标放在number-info上面,会是一个delon/chart的类库,可以在NG-ALAIN上找到阅读NG ALAIN的图表,以及number-info样式,数据文本 它拥有[title] [subtitle]两个可以是TemplateRef类型的,而template可以在里面放一些东西,比如按钮,所以可以放一个修改按钮 这里刚开始把template放…...
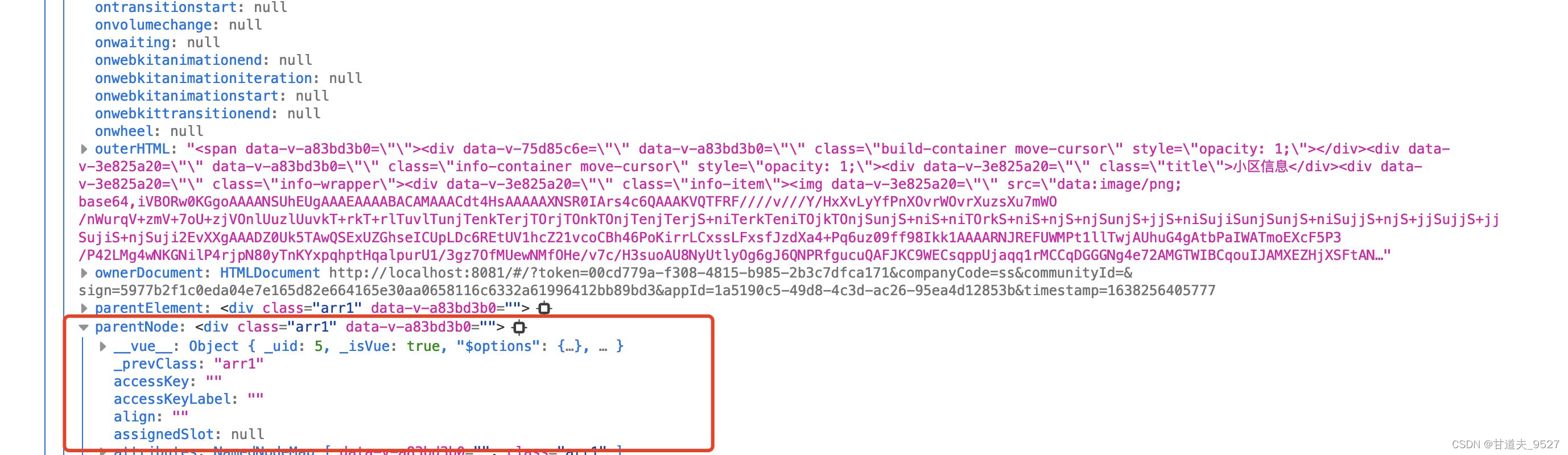
vue-draggable浏览器拖拽event事件对象拖动时 DragEvent path undefined
场景: 在做组件拖拽过程中,需要获取到触发元素冒泡过程中的所有元素,所以使用了event.path属性。在Chrome下正常运行,但是在FireFox下测试时发现,完犊子,失效了,通过问题排查,发现了…...

【云原生】搭建k8s高可用集群—20230225
文章目录多master(高可用)介绍高可用集群使用技术介绍搭建高可用k8s集群步骤1. 准备环境-系统初始化2. 在所有master节点上部署keepalived3.1 安装相关包3.2 配置master节点3.3 部署haproxy错误解决3. 所有节点安装Docker/kubeadm/kubelet4. 部署Kuberne…...

LeetCode121_121. 买卖股票的最佳时机
LeetCode121_121. 买卖股票的最佳时机 一、描述 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
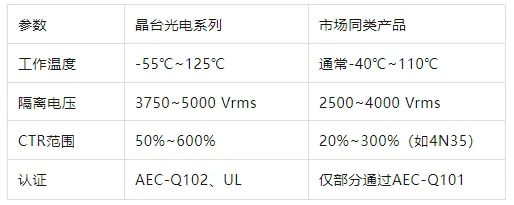
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
