堆(二叉树,带图详解)
一.堆
1.堆的概念
2.堆的存储方式
逻辑结构
物理结构
2.堆的插入问题
3.堆的基本实现(代码)(以小堆为例)
1.堆的初始化
2. 向上调整
3.插入结点
4. 交换函数、堆的打印
5.向下调整
6.删除根节点并调整成小根堆
7.获取堆顶的元素
8.判断栈是否为空
9.另一种初始化数组的方法
10.两种实现堆排序的方法的比较
二、堆的应用与实现
1.堆的升序写法
升序堆:
2.向下调整建堆(大堆)
总结
🗡CSDN主页:d1ff1cult.🗡
🗡代码云仓库:d1ff1cult.🗡
🗡文章栏目:数据结构专栏🗡
一.堆
1.堆的概念
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足: <= 且
<= ( >= 且 >= ) i = 0,1,
2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆是一种非线性结构,是完全二叉树
堆分为小根堆(小堆)和大根堆(大堆)两种,小堆中所有的父节点均小于他的子结点,大堆中所有的父结点均大于子节点。
堆的底层用数组存储
小根堆:
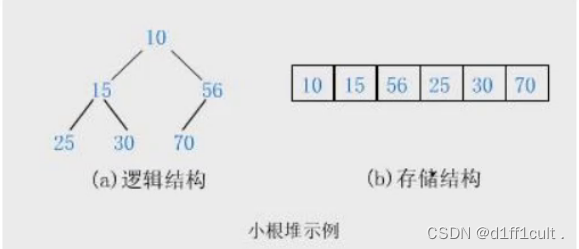
大根堆:
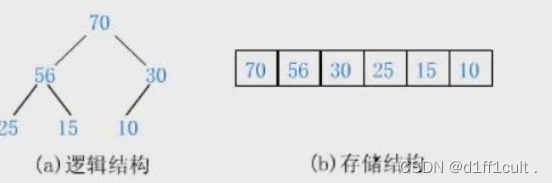
顺序存储下左右子树与父节点之间的关系:
leftchild=parent*2+1;rightchild=parent*2+2;
parent=(child-1)/2;
2.堆的存储方式
🗡逻辑结构
这里的逻辑结构是我们为了可以更好的李姐而想象出来的
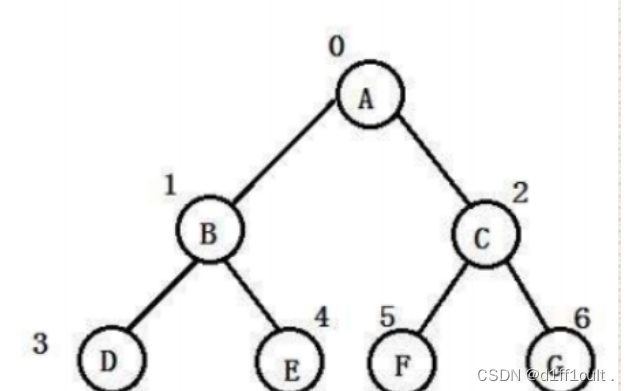
🗡物理结构
堆在内存中就是这样存储的

2.堆的插入问题


插入90我们发现该堆仍然是小堆,其实这是一个巧合,当我们插入50的时候发现该堆不再是一个小堆,我们此时需要不断地对50进行调整才能使得该堆重新成为小堆。
接下来继续向堆中插入一个5
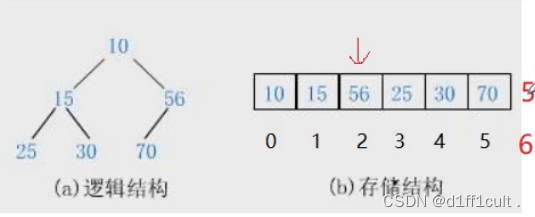
插入数据后调整的基本思路:此时5的下标为6,根据5的下标找到5的父亲结点(5-1)/2=2 ,5的父亲结点为56,再让5与56比较大小,发现56>5所以将56和5的位置进行交换,再继续让交换后的5找父亲节点,5的父亲结点的下标为(2-1)/2=0,5的父亲结点为10,再将5与10继续比较,10>5进行交换,此时5的下标为0为根节点,调整完毕。
第一次进行交换:56与5进行比较 5<56 交换5和56
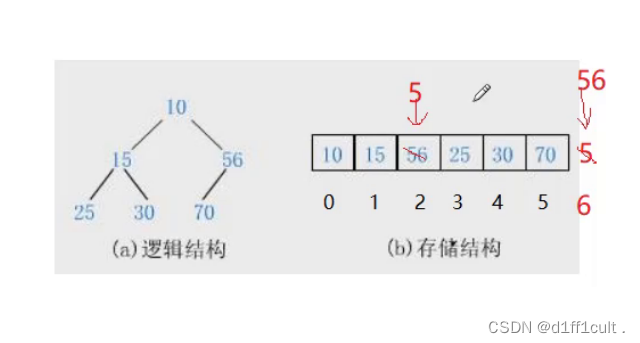
第二次进行交换: 找到交换后的5的父节点10,将10与5进行比较5<10则交换5与10的位置

很奇怪,这个最后插入的5 从孙子一跃成为了爷爷(bushi
3.堆的基本实现(代码)(以小堆为例)
下面介绍几个主要的实现堆的函数。
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
void Swap(HPDataType* a, HPDataType* b);
void HeapPrint(HP* php);
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a,int n,int parent);
bool HeapEmpty(HP* php);
void HeapInitArray(HP* php, int* a, int n);
void HeapSor🗡堆的初始化
将数组和容量以及数组大小全部置空。
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->size = 0;
}🗡向上调整
将插入的结点一步步调整,使该堆再次成为小堆
向上调整的前提:前面的数据是堆
AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}🗡插入结点
插入一个结点,并将其调整成为一个小堆
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);
}🗡交换函数、堆的打印
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//交换函数
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}//堆的打印函数🗡向下调整
向下调整的前提:根结点左右子树都是堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while(child<n){if (child+1<n&&a[child] > a[child + 1])//保证child存的是左右孩子里面较小的那一个{++child;}if (a[child] < a[parent])// 父节点与两个儿子中较小的一个交换位置{Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}else{break;}}
}🗡删除根节点并调整成小根堆
void HeapPop(HP* php)
{assert(php); assert(php->size > 0);Swap(&php->a[0], php->a[php->size - 1]);--php->size;AdjustDowm(php->a, php->size, 0);
}
🗡获取堆顶的元素
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}🗡判断栈是否为空
bool HeapEmpty(HP* php){assert(php);return php->size == 0;}🗡另一种初始化数组的方法
void HeapInitArray(HP* php, int* a, int n){assert(php);assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){perror("malloc fail");exit(-1);}php->size = n;php->capacity = n;memcpy(php->a, a, sizeof(HPDataType) * n); for (int i = 0; i < n; i++){AdjustUp(php->a, i);}}🗡两种实现堆排序的方法的比较
下面是使用HeapPush()函数实现堆排的过程 :
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);
}这种方法是通过malloc函数开辟一块一块的空间,并通过不断地扩容将数据push到数组中,再对数组中的内容进行不断的向上调整从而达到堆排的目的。
下面是用AdjustUp()函数实现堆排的过程:
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}
void HeapSort(int* a, int n)
{for (int i = 0; i < n; i++){AdjustUp(a, i);}
}这种方法与HeapPush函数不同的地方在于该函数传参数时直接传入一个数组,省去了malloc开辟空间的消耗。
二、堆的应用与实现
🗡堆的升序写法
通常这里我们都会问一个问题,实现升序排序我们应该建一个小堆还是一个大堆?
答案是,升序时我们应该建一个大堆,那么为什么呢?
我们都知道小堆的根节点是整棵二叉树中最小的值,选出了最小的值之后,我们还要去找次小的值
首先是建小堆不适用的原因,这里有这样一个数组,我们将这个数组展开:
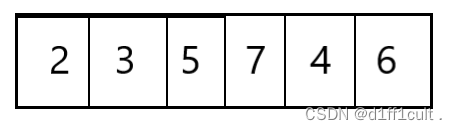
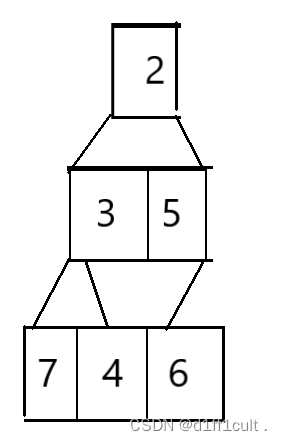
按照我们需要建升序堆的要求,我们会将最小的根节点删除掉,删除后如下图所示
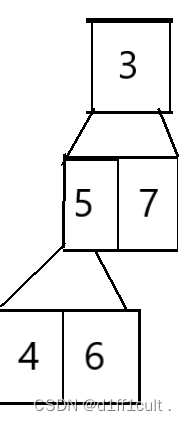
我们发现这个二叉树不再是堆,但是我们要选择次小值的话需要进行调整,就需要重新建堆,建堆的时间复杂度为o(n)=n*logn,代价还是比较大的,甚至不如遍历一遍来的快,所以我们这里摒弃了建小堆的想法,那么接下来就看看建大堆的优势在哪里了
建大堆的基本思想以及优势:
我们排升序,建一个大堆,将根节点和最后一个结点交换位置,那么最大的数就被交换到了数组的最后面,此时一个数字已经排好了,原本根节点的左右子树还是堆,我们就可以通过向下调整,来找出次打的值,此时我们不再把交换到数组最后的根节点看作树的结点,对剩下的数字进行向下调整,找出了次小的值,这里的时间复杂度O(n)仅仅为logn合计起来n个结点的时间复杂度O(n)=n*logn,消耗比较小。再与树的最后一个结点进行交换。过程我们用下面的数组进行演示。

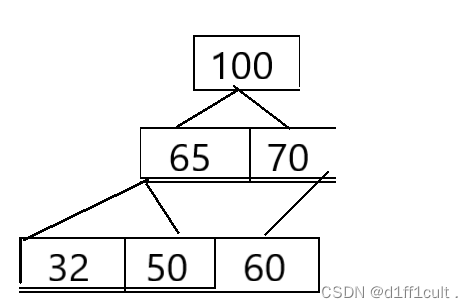
将根节点的数字与树的最后一个结点的数字进行交换,并不再把交换到后面的根节点看作树的内容
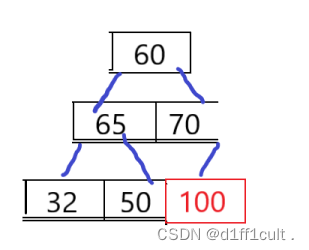
🗡升序堆:
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while(child<n){if (child+1<n&&a[child] > a[child + 1])//保证child存的是左右孩子里面较小的那一个{++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{for (int i = 0; i < n; i++){AdjustUp(a, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}🗡向下调整建堆(大堆)
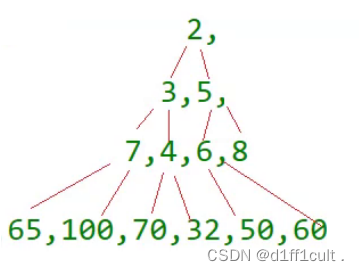
有这样一个数组,我们如果想通过用根节点直接向下调整建大堆,就必须保证根节点的左右子树都是大堆,所以我们就想出了倒着调整树的方法:
需要注意的是:单个叶子结点,既是大堆也是小堆。
这种建堆方法是从树的末尾开始找到第一个非叶子结点然后对其进行向下调整,从数组后面查找的第一个非叶子结点也就是树中最后一个结点的父节点,最后一个结点的下标为n-1,则它的父结点的下标为(n-1-1)/2 ,这棵树从后面查找的第一个非叶子结点是6,对6进行向下调整,如下图
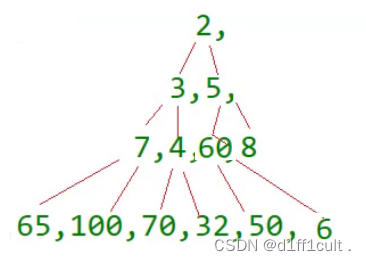
我们发现调整完成之后,结点5的左子树已经成为了大堆,右子树也是大堆,那我们就应该对下一个非叶子结点进行调整了,我们只需要将60位置的下标+1,就得到了下一个非叶子结点的下标,同理也对他进行调整,直到2的左右子树都调整为大堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while(child<n){if (child+1<n&&a[child] > a[child + 1])//保证child存的是左右孩子里面较小的那一个{++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{//向上调整建堆(大堆或者小堆)//for (int i = 0; i < n; i++)//{// AdjustUp(a, i);//}//向下调整建堆for (int i = (n - 2) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}向上调整建堆,时间复杂度O(n)=n*logn,而向下调整建堆的时间复杂度O(n)=n.
总结
上述就是关于堆的一些知识,有不懂的地方欢迎提问。
相关文章:

堆(二叉树,带图详解)
一.堆 1.堆的概念 2.堆的存储方式 逻辑结构 物理结构 2.堆的插入问题 3.堆的基本实现(代码)(以小堆为例) 1.堆的初始化 2. 向上调整 3.插入结点 4. 交换函数、堆的打印 5.向下调整 6.删除根节点并调整成小根堆 7.获取堆…...
vue3 code format bug
vue code format bug vue客户端代码格式化缺陷,为了方便阅读和维护,对代码格式化发现这个缺陷 vue.global.min.3.2.26.js var Vuefunction(r){"use strict";function e(e,t){const nObject.create(null);var re.split(",");for(le…...

7-3、S曲线生成器【51单片机控制步进电机-TB6600系列】
摘要:本节介绍步进电机S曲线生成器的计算以及使用 一.计算原理 根据上一节内容,已经计算了一条任意S曲线的函数。在步进电机S曲线加减速的控制中,需要的S曲线如图1所示,横轴为时间,纵轴为角速度,其中w0为起…...
CDC实时数据同步
一丶CDC实时数据同步介绍 CDC实时数据同步指的是Change Data Capture(数据变更捕获)技术在数据同步过程中的应用。CDC技术允许在数据源发生变化时,实时地捕获这些变化,并将其应用到目标系统中,从而保持数据的同步性。…...
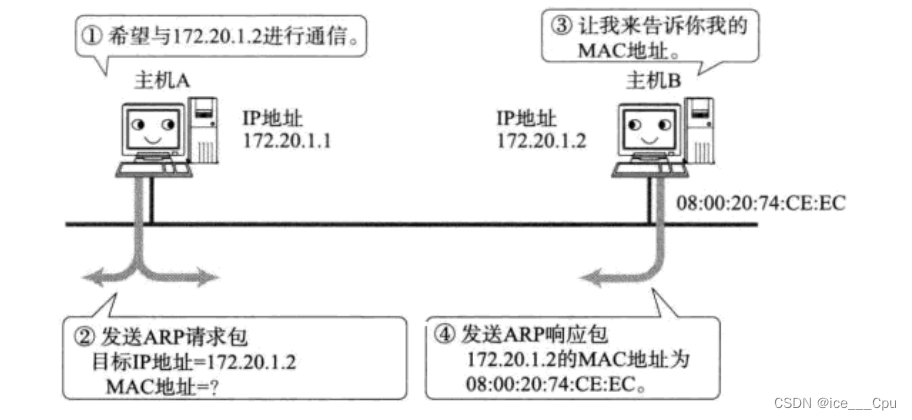
javaEE -10(11000字详解5层重要协议)
一:应用层重点协议 1.1: DNS DNS,即Domain Name System,域名系统。DNS是一整套从域名映射到IP的系统。 TCP/IP中使用IP地址来确定网络上的一台主机,但是IP地址不方便记忆,且不能表达地址组织信息&#x…...

360智慧生活旗舰产品率先接入“360智脑”能力实现升级
10月25日,360智慧生活秋季新品及视觉云方案发布会在深圳召开。360智能硬件产品,诸如 360可视门铃、360智能摄像机、360行车记录仪、360儿童手表和家庭防火墙等,都在各自的行业有着举足轻重得地位,而这次发布的系列新品,…...

【系统架构设计】 架构核心知识: 2 云原生架构
目录 一 云原生架构 1 云计算 2 分类 3 云计算架构 4 云原生架构设计原则...
Unity - 导出的FBX模型,无法将 vector4 保存在 uv 中(使用 Unity Mesh 保存即可)
文章目录 目的问题解决方案验证保存为 Unity Mesh 结果 - OK保存为 *.obj 文件结果 - not OK,但是可以 DIY importer注意References 目的 备忘,便于日后自己索引 问题 为了学习了解大厂项目的效果: 上周为了将 王者荣耀的 杨玉环 的某个皮肤…...

【疯狂Java】数组
1、一维数组 (1)初始化 ①静态初始化:只指定元素,不指定长度 new 类型[] {元素1,元素2,...} int[] intArr; intArr new int[] {5,6,7,8}; ②动态初始化:只指定长度,不指定元素 new 类型[数组长度] int[] princes new in…...

leetcode 503. 下一个更大元素 II、42. 接雨水
下一个更大元素 II 给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。 数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数&…...
【德哥说库系列】-PostgreSQL跨版本升级
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
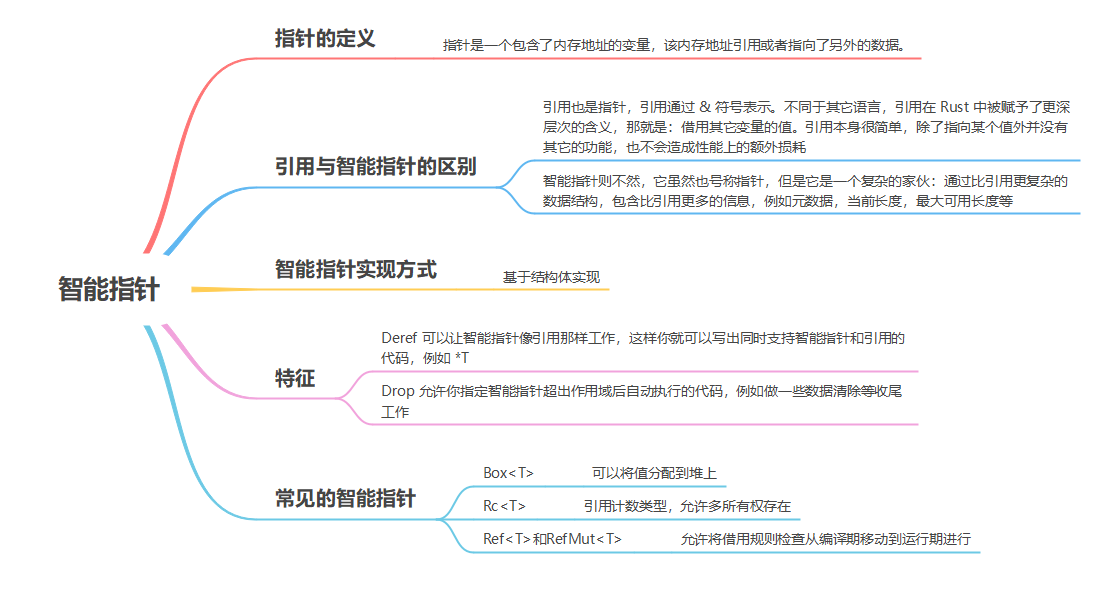
rust学习——智能指针
智能指针 在各个编程语言中,指针的概念几乎都是相同的:指针是一个包含了内存地址的变量,该内存地址引用或者指向了另外的数据。 在 Rust 中,最常见的指针类型是引用,引用通过 & 符号表示。不同于其它语言…...

系列一、Spring Framework
一、谈谈你对Spring的理解 Spring是一个生态,是一个轻量级的开源容器框架,可以构建Java应用所需要的一切基础设施,它的出现是为了解决企业级应用开发中业务逻辑层和其他各层对象与对象之间耦合的问题,通常情况下所说的Spring是指S…...

PULP Ubuntu18.04
1. 安装eda工具:questasim_10.7_linux64,网上有教程和方法,如有问题,可私信我 2. 代码下载: git clone https://github.com/pulp-platform/pulp 编译代码 cd pulp source setup/vsim.sh make checkout make scripts …...

Docker harbor私有仓库部与管理
目录 搭建本地私有仓库 Docker容器的重启策略 Harbor 简介 什么是Harbor Harbor的特性 Harbor的构成 Docker harbor私有仓库部署 Harbor.cfg配置文件中的参数 维护管理Harbor 总结 搭建本地私有仓库 #首先下载 registry 镜像 docker pull registry#在 daemon.json …...
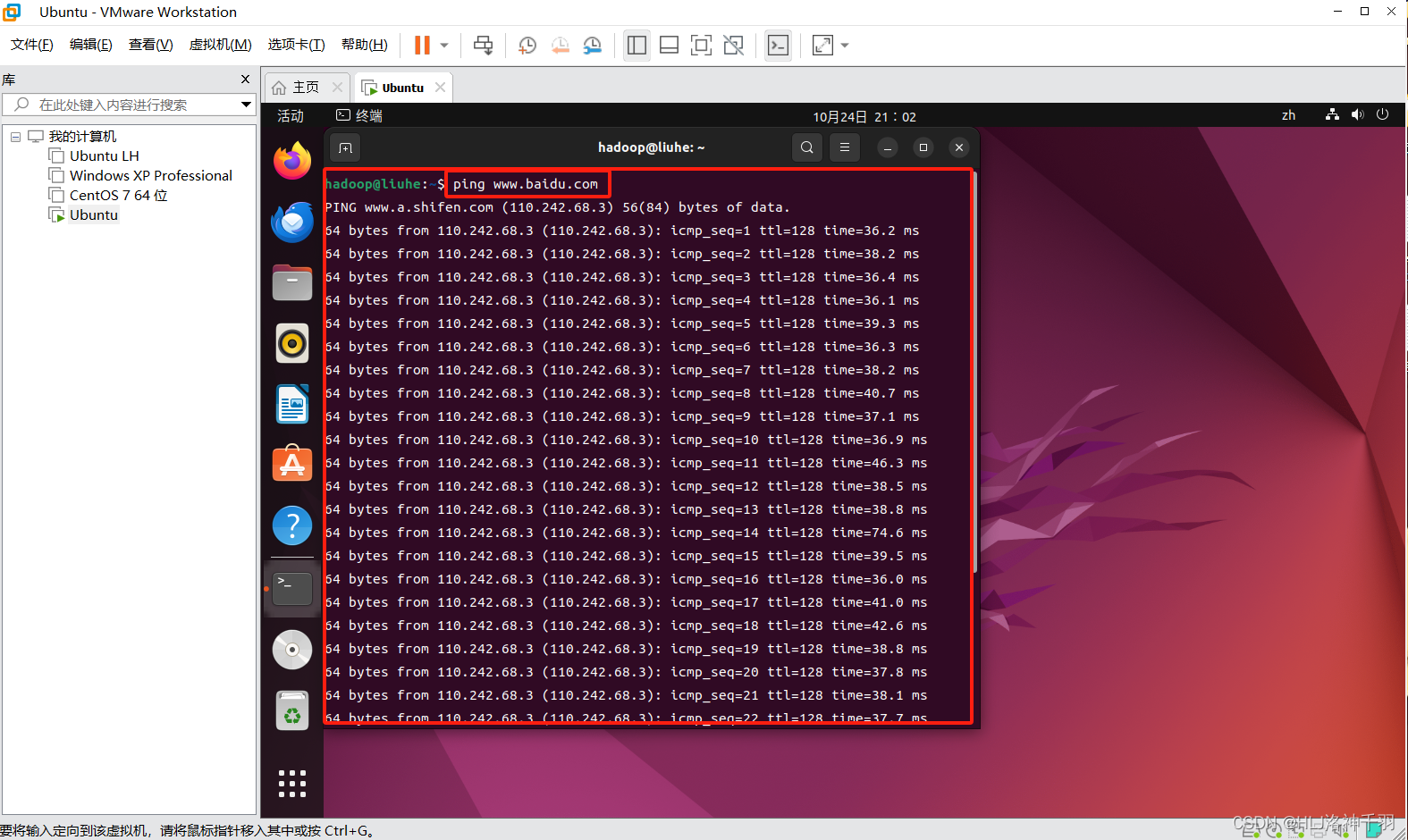
解决虚拟机联网问题
虚拟机开机后发现右上角缺少联网标志(下面有正常联网标志),这样就是连不上网的 不信你可以打开Ubuntu里面的浏览器或ping www.baidu.com 1.编辑虚拟机设置-->网络适配器-->如图所示 2.选择编辑-->虚拟网络编辑器 3.更改设置 4此处可以选择还原默认设置&am…...
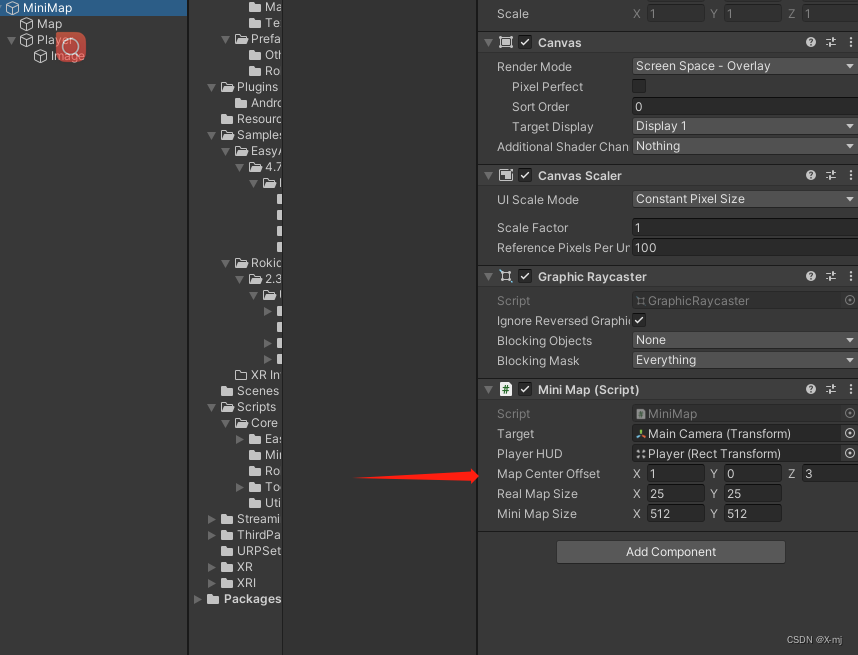
Unity 自定义小地图
最近工作做了个小地图,再此记录下思路。 1、准备所需素材 显示为地图(我们取顶视图)。创建一个Cube,缩放到可以把实际地图包住。实际地图的尺寸和偏移量 。我这里长宽都是25,偏移量(1,0&…...

力扣每日一题66:加一
题目描述: 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。 示例 1: 输…...
项目管理工具ConceptDraw PROJECT mac中文版自定义列功能
ConceptDraw PROJECT Mac是一款专业的项目管理工具,适用于MacOS平台。它提供了成功规划和执行项目所需的完整功能,包括任务和资源管理、报告和变更控制。 这款软件可以与ConceptDraw office集成,利用思维导图和数据可视化的强大功能来改进项目…...

Kafka-Java二:Spring实现kafka消息发送的ack机制
写在前面 如果只有一个kafka实例的话,那么文章中提到kafka集群kafka实例 一、什么是消息发送者端的ack机制 ack机制:消息确认发送成功的标识 由谁发起该标识:kafka集群 发起该标识的场景:kafka集群确认已经收到了消息。 由谁接收…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
