【机器学习合集】激活函数合集 ->(个人学习记录笔记)
文章目录
- 综述
- 1. S激活函数(sigmoid&Tanh)
- 2. ReLU激活函数
- 3. ReLU激活函数的改进
- 4. 近似ReLU激活函数
- 5. Maxout激活函数
- 6. 自动搜索的激活函数Swish
综述
这些都是神经网络中常用的激活函数,它们在非线性变换方面有不同的特点。以下是这些激活函数的主要区别:
Sigmoid和Tanh激活函数:
- Sigmoid函数和Tanh函数都是S型函数,将输入映射到(0,1)或(-1,1)范围内。它们在输入远离零时会饱和,导致梯度消失问题。
- Sigmoid函数输出范围是(0,1),而Tanh函数输出范围是(-1,1)。
- 在深度神经网络中,它们往往不如ReLU等其他激活函数表现出色。
ReLU激活函数(Rectified Linear Unit):
- ReLU是分段线性函数,当输入为正时输出等于输入,而当输入为负时输出为零。
- ReLU激活函数在训练深度神经网络时通常表现良好,因为它不会导致梯度消失问题,并且计算速度快。
- 然而,它也有一些问题,如死亡神经元问题,即某些神经元在训练中可能永远不会激活。
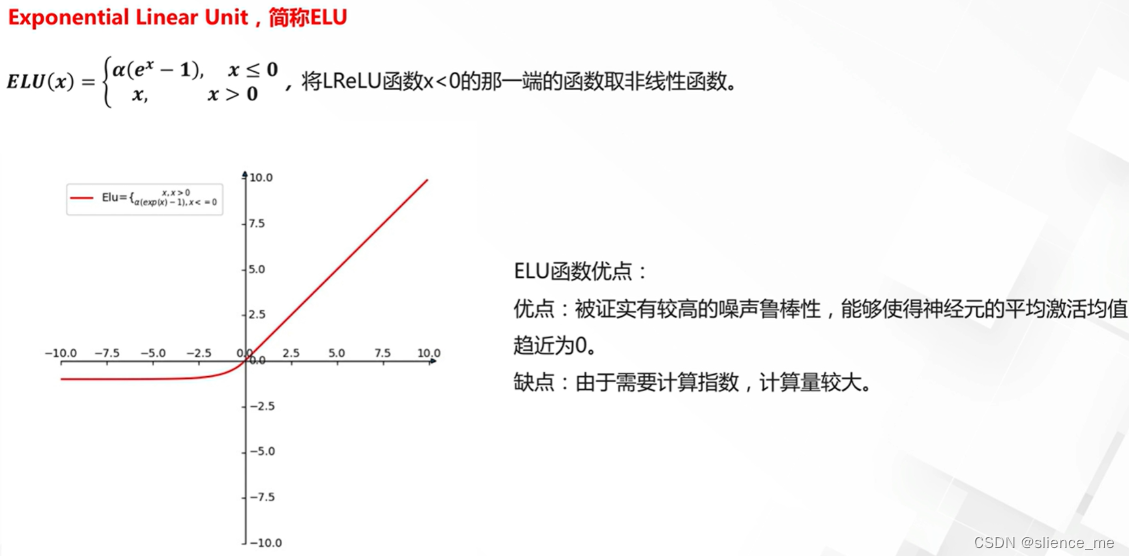
ReLU激活函数的改进(Leaky ReLU、Parametric ReLU、Exponential Linear Unit等):
- 这些是ReLU的改进版本,旨在解决死亡神经元问题。它们允许小的负输入值通过,从而改善了ReLU的性能。
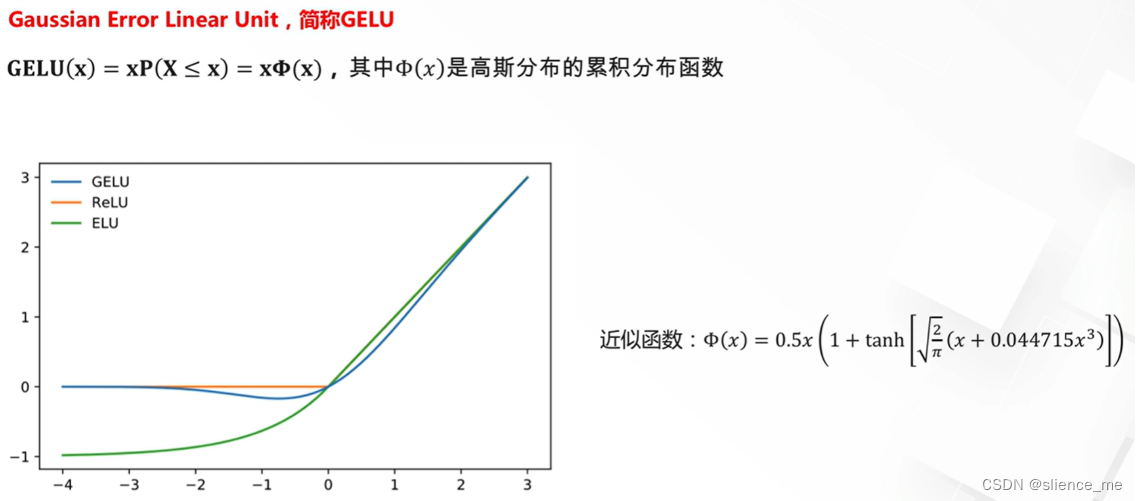
近似ReLU激活函数(Swish、Mish等):
- 近似ReLU函数试图在ReLu的非线性性和平滑性之间取得平衡。Swish和Mish是其中的两个例子,它们在输入大于零时光滑且非线性,但在输入小于零时也具有一定的非线性性。
- Swish是x乘以S型函数,而Mish是x与双曲正切函数的乘积。这些函数在某些情况下可以表现出色,但并不总是适用于所有情况。
Maxout激活函数:
- Maxout是一种非线性激活函数,它在每个神经元的输入中选择最大的那个。它的输出是线性的片段中的最大值。
- Maxout激活函数允许网络自行学习不同的线性片段,从而提高网络的表达能力。
自动搜索的激活函数(Swish等):
- Swish是通过自动搜索和优化得到的激活函数。它的设计基于一定的数学原理和实验结果,旨在提高神经网络的性能。
- 这些自动搜索得到的激活函数通常经过大量实验验证,以确保它们在各种任务中表现良好。
- 每种激活函数都有其适用的场景和优点,选择哪种激活函数通常取决于具体的任务和网络结构。在深度学习中,通常需要进行实验来确定哪种激活函数在特定情况下效果最好
1. S激活函数(sigmoid&Tanh)
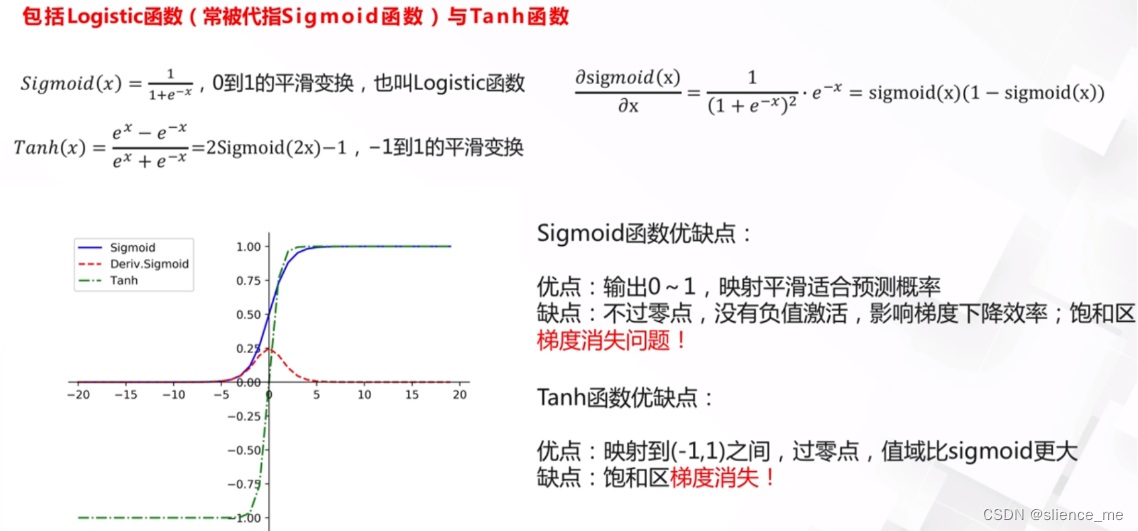
Sigmoid函数在机器学习中经常用作激活函数,但它在某些情况下容易出现梯度消失问题,这是因为它的特性导致了梯度在饱和区域非常接近于零。
Sigmoid函数的数学表达式如下: S(x) = 1 / (1 + e^(-x))
- 当输入x接近正无穷大(x → +∞)时,Sigmoid函数的输出趋近于1,而当输入x接近负无穷大(x → -∞)时,输出趋近于0。这意味着Sigmoid函数具有饱和性质,即在这些极端值附近,它的梯度接近于零。这就是梯度消失问题的根本原因。
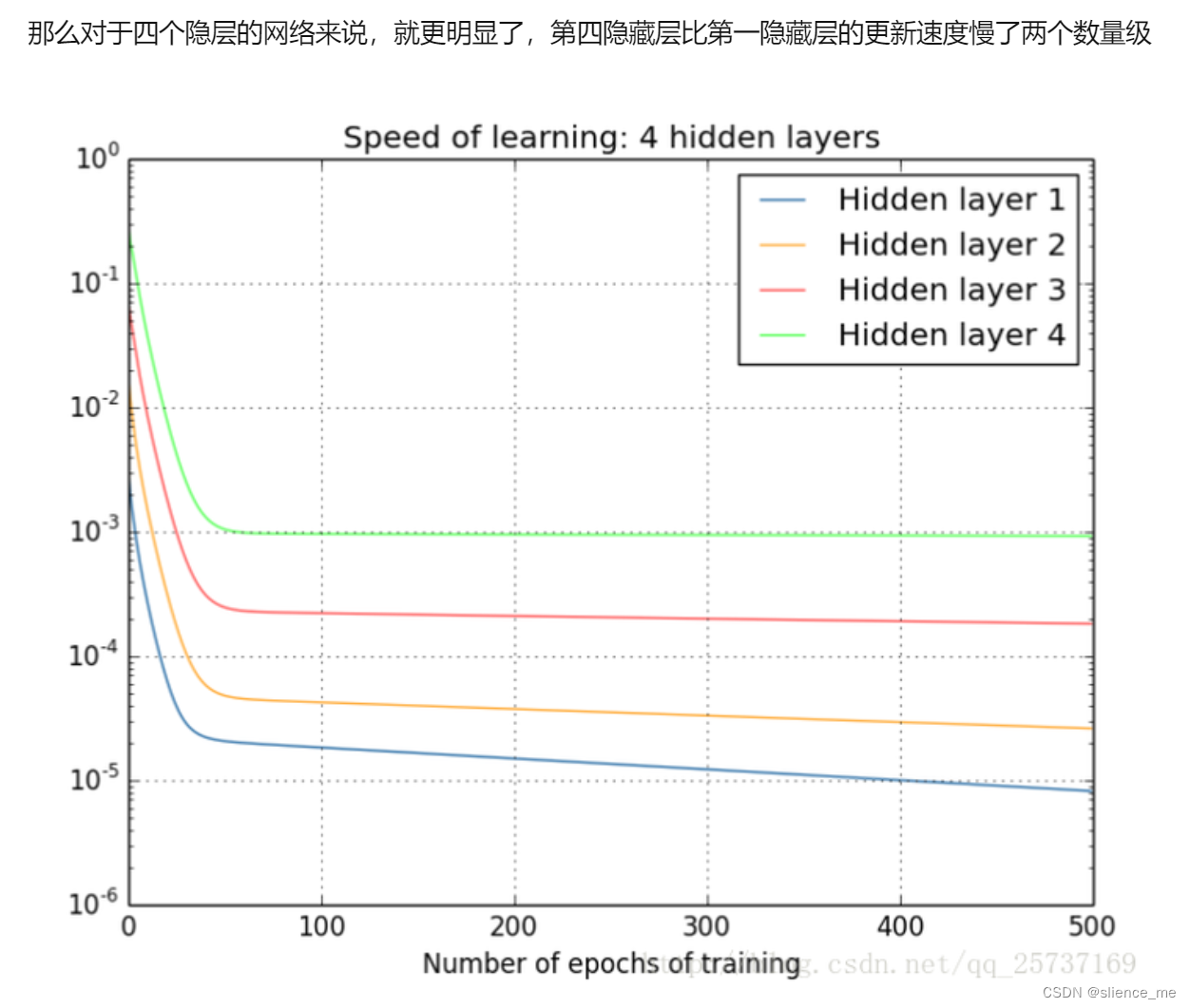
- 当你使用Sigmoid激活函数时,如果输入数据的绝对值非常大,梯度接近于零,这会导致反向传播算法中的梯度变得非常小,从而权重更新几乎不会发生,导致训练变得非常缓慢或根本无法进行有效的学习。这尤其在深度神经网络中更加明显,因为梯度会以指数方式递减,这就是为什么Sigmoid函数在深度神经网络中容易出现梯度消失问题。
- 为了克服这个问题,人们开始使用其他激活函数,如ReLU(Rectified Linear Unit)和其变种,它们不具有Sigmoid函数的饱和性质,因此在训练深度神经网络时更加稳定。ReLU激活函数的导数在正区域始终为1,因此梯度不会在正区域消失。这有助于更有效地进行梯度传播和权重更新,减少了梯度消失问题。


- Tanh(双曲正切)函数在某些情况下也可能出现梯度消失问题,尽管它相对于Sigmoid函数有一些改进,但仍然具有饱和性质,导致梯度在饱和区域接近于零。
- Tanh函数的数学表达式如下: Tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
- Tanh函数的输出范围在-1到1之间,当输入x接近正无穷大时,它的输出趋近于1,当输入x接近负无穷大时,它的输出趋近于-1。这就意味着Tanh函数在极端值附近也具有饱和性质,梯度接近于零。
- 梯度消失问题发生的原因在于反向传播算法中的链式法则,其中导数相乘。当使用Tanh函数时,如果在网络的前向传播过程中输出值位于饱和区域,梯度将变得非常小,反向传播中的梯度也会随之减小。这会导致权重更新非常缓慢,尤其是在深度神经网络中。
- 虽然Tanh函数相对于Sigmoid函数在某些情况下更好,因为它的输出范围在-1到1之间,但在解决梯度消失问题方面,它仍然不如一些其他激活函数,如ReLU(Rectified Linear Unit)及其变种。ReLU在正区域具有恒定梯度,因此不容易出现梯度消失问题。为了克服梯度消失问题,深度神经网络中的一种常见做法是使用ReLU或其变种,同时采用一些正则化技术和初始化策略来稳定训练过程。
2. ReLU激活函数
- ReLU(Rectified Linear Unit)是一种常用的激活函数,它在输入大于零时输出输入值,而在输入小于或等于零时输出零。这意味着ReLU是非零中心化的,因为它的输出的均值(平均值)不是零,而是正的。这与一些其他激活函数,如tanh和Sigmoid不同,它们的输出均值通常接近于零。
- 为什么ReLU是非零中心化的并且没有负激活值,可以归结为其定义方式。ReLU函数的数学表达式如下: f(x) = max(0, x)
- 在这个函数中,当输入x大于零时,它输出x,而当输入x小于等于零时,输出零。这意味着ReLU在正区域(x>0)内有激活值,但在负区域(x<=0)内没有激活值。因为ReLU截断了负值,所以其均值是正的。
- 这种非零中心化的性质有一些影响:
- 梯度消失问题缓解:与tanh和Sigmoid等激活函数不同,ReLU在正区域的梯度始终为1,这有助于减轻梯度消失问题,因为梯度不会在正区域消失。
- 稀疏激活性:由于ReLU在负区域没有激活值,神经元可以学习选择性地激活,这有助于网络的稀疏表示,这意味着每个神经元仅在特定情况下激活,而其他时候保持静止,这对于特征选择和表示学习很有用。
- 尽管ReLU有许多优点,但它也有一些问题,例如死亡神经元问题,其中某些神经元在训练中永远保持非活跃状态。为了克服这些问题,人们发展了一些ReLU的变种,如Leaky ReLU和Parametric ReLU(PReLU),它们允许小的负输入值通过,从而改善了ReLU的性能。这些变种可以使神经网络更容易训练。
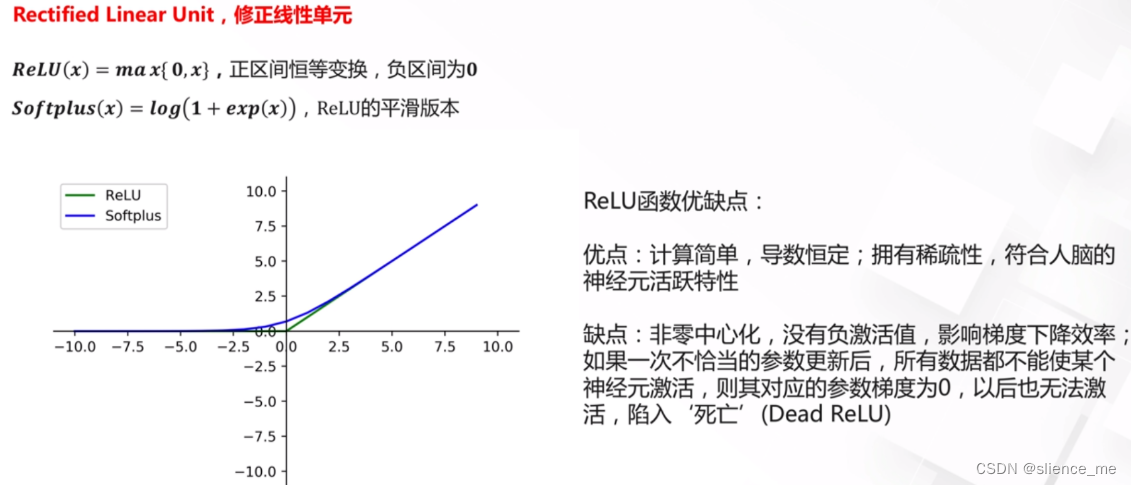
3. ReLU激活函数的改进
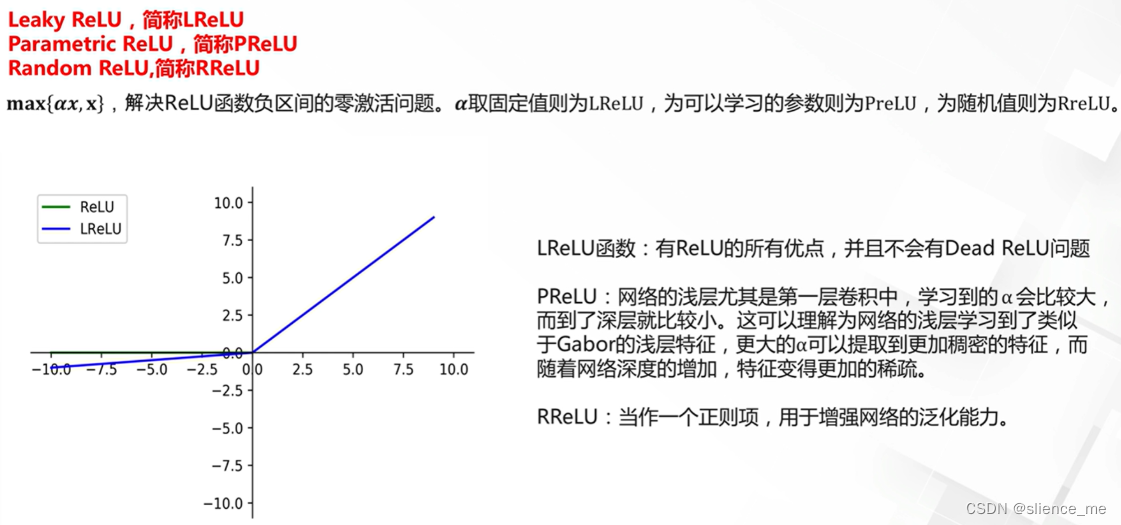
4. 近似ReLU激活函数
5. Maxout激活函数
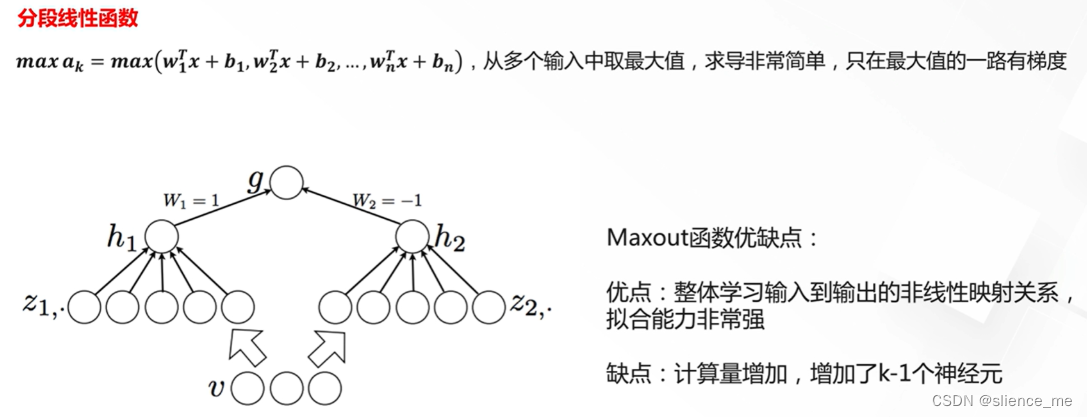
- Maxout是一种激活函数,它在深度学习中用于神经网络的非线性变换。与传统的激活函数如ReLU、Sigmoid和tanh不同,Maxout具有独特的结构,它的主要特点是取输入的最大值,因此可以视为线性片段的极大化。以下是Maxout激活函数的定义:
- 对于Maxout激活函数,给定多个线性组合的输入,它将这些线性组合中的最大值作为输出。具体来说,考虑两个线性组合:
Z1 = w1x + b1
Z2 = w2x + b2- Maxout激活函数输出的值为:Maxout(x) = max(Z1, Z2)
- Maxout的主要特点和优点包括:
- 非线性性质:Maxout函数是一种非线性激活函数,因为它取输入中的最大值,从而引入了非线性性质,使神经网络能够学习更复杂的函数。
- 灵活性:Maxout允许神经网络学习不同的线性片段,而不受限于单一的线性关系。这可以增加模型的表达能力,有助于处理各种数据分布和特征。
- 抗噪声性:Maxout激活函数在一定程度上对噪声具有抗性,因为它取输入中的最大值,可以消除一些不必要的噪声信号。
- 降低过拟合风险:Maxout具有更多的参数,允许网络在训练中拟合更多的数据,从而降低了过拟合的风险。
- 尽管Maxout在理论上具有一些优势,但在实际应用中,它并不像ReLU那样常见。这是因为Maxout的参数数量较多,可能需要更多的数据和计算资源来训练。此外,ReLU和其变种在实践中通常表现得非常出色,因此它们更常见。然而,Maxout仍然是一个有趣的激活函数,特别适用于特定的深度学习任务和研究领域。
6. 自动搜索的激活函数Swish
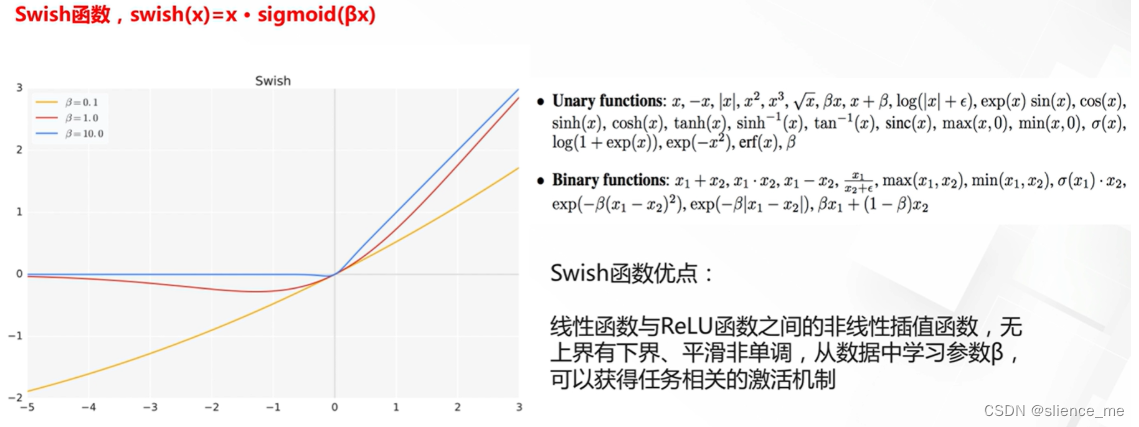
- Swish是一种激活函数,最初由Google研究员在2017年提出。Swish函数的定义如下:Swish(x) = x * sigmoid(x)
- 其中,x是输入,sigmoid(x)表示x经过S型函数(Sigmoid函数)的输出。Swish函数是一种非线性激活函数,它在一定程度上结合了线性和非线性的特性。
- Swish函数的特点和优势包括:
- 平滑性:Swish函数是平滑的,与ReLU等分段线性函数相比,它在激活值的变化上更加平滑。这有助于梯度的更加连续传播,有助于训练深度神经网络。
- 非线性性质:Swish在Sigmoid函数的基础上引入了非线性,这使得它能够捕捉更复杂的数据模式,使神经网络更具表达能力。
- 渐进性:与ReLU不同,Swish函数在输入趋于正无穷大时不会饱和,而是渐进地接近于线性函数x。这意味着Swish函数在正值区域仍然具有一定的非线性性质,从而有助于避免一些梯度消失问题。
- 可学习性:Swish函数是可学习的,它的参数(例如,Sigmoid函数的斜率)可以通过反向传播算法进行调整,以适应特定任务和数据分布。
- 尽管Swish在理论上有一些优势,但在实践中,它的性能通常介于ReLU和Sigmoid之间。因此,选择使用Swish还是其他激活函数取决于具体的任务和实验。有时,Swish可能对某些问题效果很好,但对于其他问题,标准的ReLU或其变种仍然是首选。在深度学习中,激活函数通常是可以调整的超参数,因此可以进行实验来选择最适合特定任务的激活函数。
注意:部分内容来自 阿里云天池
相关文章:

【机器学习合集】激活函数合集 ->(个人学习记录笔记)
文章目录 综述1. S激活函数(sigmoid&Tanh)2. ReLU激活函数3. ReLU激活函数的改进4. 近似ReLU激活函数5. Maxout激活函数6. 自动搜索的激活函数Swish 综述 这些都是神经网络中常用的激活函数,它们在非线性变换方面有不同的特点。以下是这些激活函数的主要区别&am…...

【从0到1设计一个网关】什么是网关?以及为什么需要自研网关?
文章目录 什么是网关?网关类型网关的优缺点目前的网关解决方案有哪些?为什么要自研Gateway网关?自研网关需要注意什么? 注: 这篇文章作为我的网关的第一篇文章,并不涉及任何代码,只是提及了网关…...

Tp框架如何使用事务和锁,还有查询缓存
1.事务 在ThinkPHP框架中,可以使用think\db\Transaction类来实现事务。 use think\Db; use think\db\Transaction;// 开始事务 Db::startTrans();try {// 执行数据库操作Db::table(user)->where(id, 1)->update([name > John]);// 提交事务Db::commit(); }…...
Java IDEA feign调用上传文件MultipartFile以及实体对象亲测可行
Java IDEA feign调用上传文件MultipartFile以及实体对象亲测可行 1. 报错 java.lang.IllegalStateException: Body parameter cannot be used with form parameters2. 解决参考 1. 报错 java.lang.IllegalStateException: Body parameter cannot be used with form parameters …...
【产品经理】APP备案(阿里云)
工信部《关于开展移动互联网应用程序备案工作的通知》 工业和信息化部印发了《关于开展移动互联网应用程序备案工作的通知》,“在中华人民共和国境内从事互联网信息服务的App主办者,应当依照相关法律法规等规定履行备案手续,未履行备案手续的…...

Overmind VS Redux
Overmind Overmind 是一个状态管理库,它可以帮助你管理应用程序的状态和副作用。下面是一个使用 Overmind 的简单示例: 首先,我们需要安装 Overmind 和它的 React 绑定: npm install overmind overmind-react然后,我…...

0基础学习PyFlink——流批模式在主键上的对比
假如我们将《0基础学习PyFlink——使用PyFlink的Sink将结果输出到外部系统》中的模式从批处理(batch)改成流处理(stream),则其在print连接器上产生的输出是不一样。 批处理 env_settings EnvironmentSettings \.new_…...
Java学习笔记(五)——数组、排序和查找
一、数组 (一)数组的使用 1、使用方式1——动态初始化 2、使用方式2——动态初始化 3、使用方式3——静态初始化 (二)数组使用注意事项和细节 (三)数组赋值机制 (四)数组拷贝…...
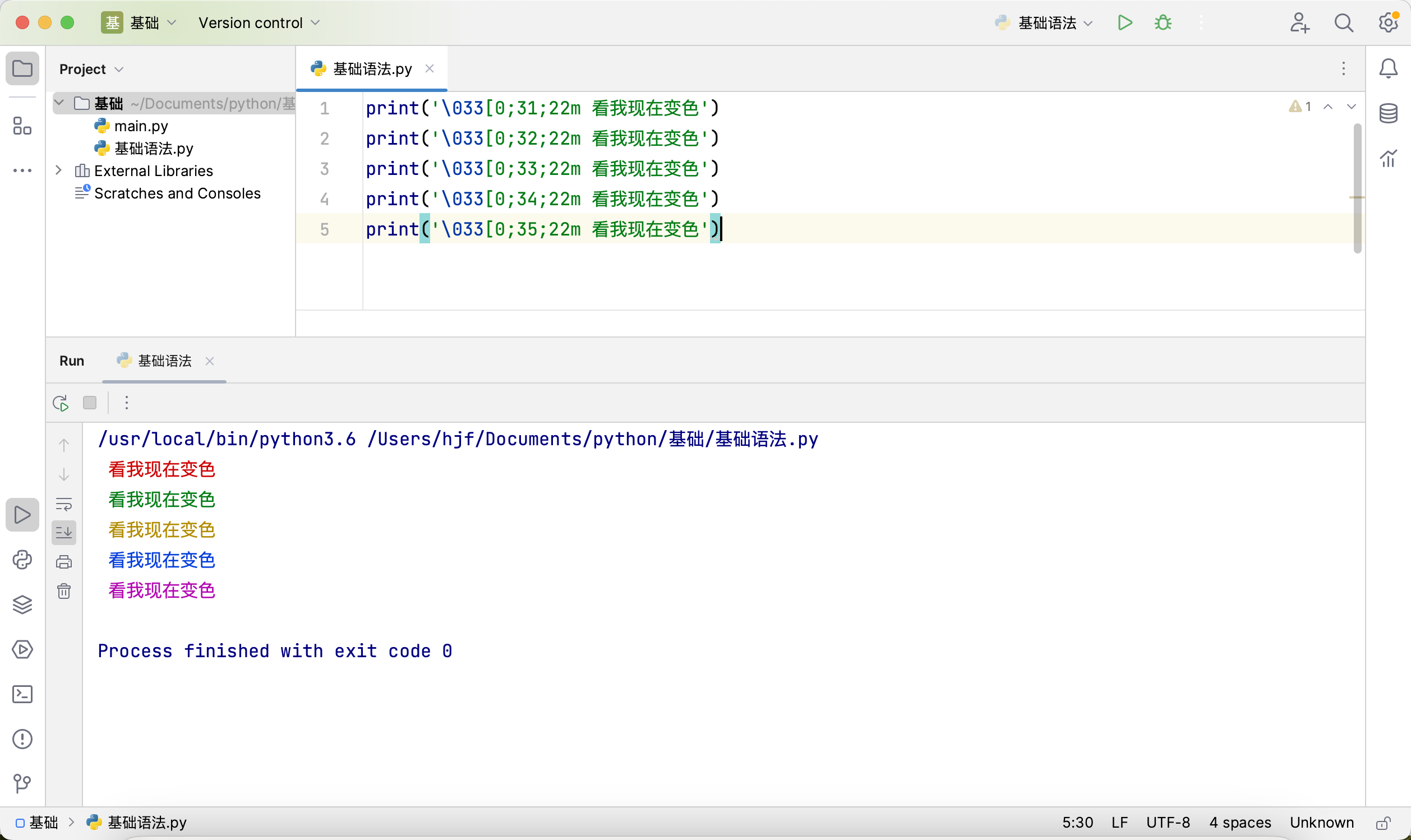
python输出与数据类型
目标 1、使用print输出内容 2、熟悉字符串类型 3、熟悉数字类型 4、熟悉数字与字符串操作 输出 print可控制输出内容也可配合、-、*、/进行运算,和整数型配合可进行运算和字符型配合有不同效果,如为拼接,*为多次输出注:整数型如&…...

React-Redux总结含购物车案例
React-Redux总结含购物车案例 reduc简介 redux是react全家桶的一员,它为react给i共可预测化的状态管理机制。redux是将整个应用状态存储到一个地方,成为store,里面存放着一颗树状态(state,tree),组件可以派发dispatch行为action给store,而不是直接通知其…...

攻克组合优化问题!美国DARPA选中全栈量子经典计算公司Rigetti
(图片来源:网络) 近日,美国量子计算公司Rigetti宣布,它被美国国防高级研究计划局 (DARPA) 选中,加入想象未来量子实际应用 (IMPAQT) 计划,推进先进量子算法的研发,去解决组合优化问…...
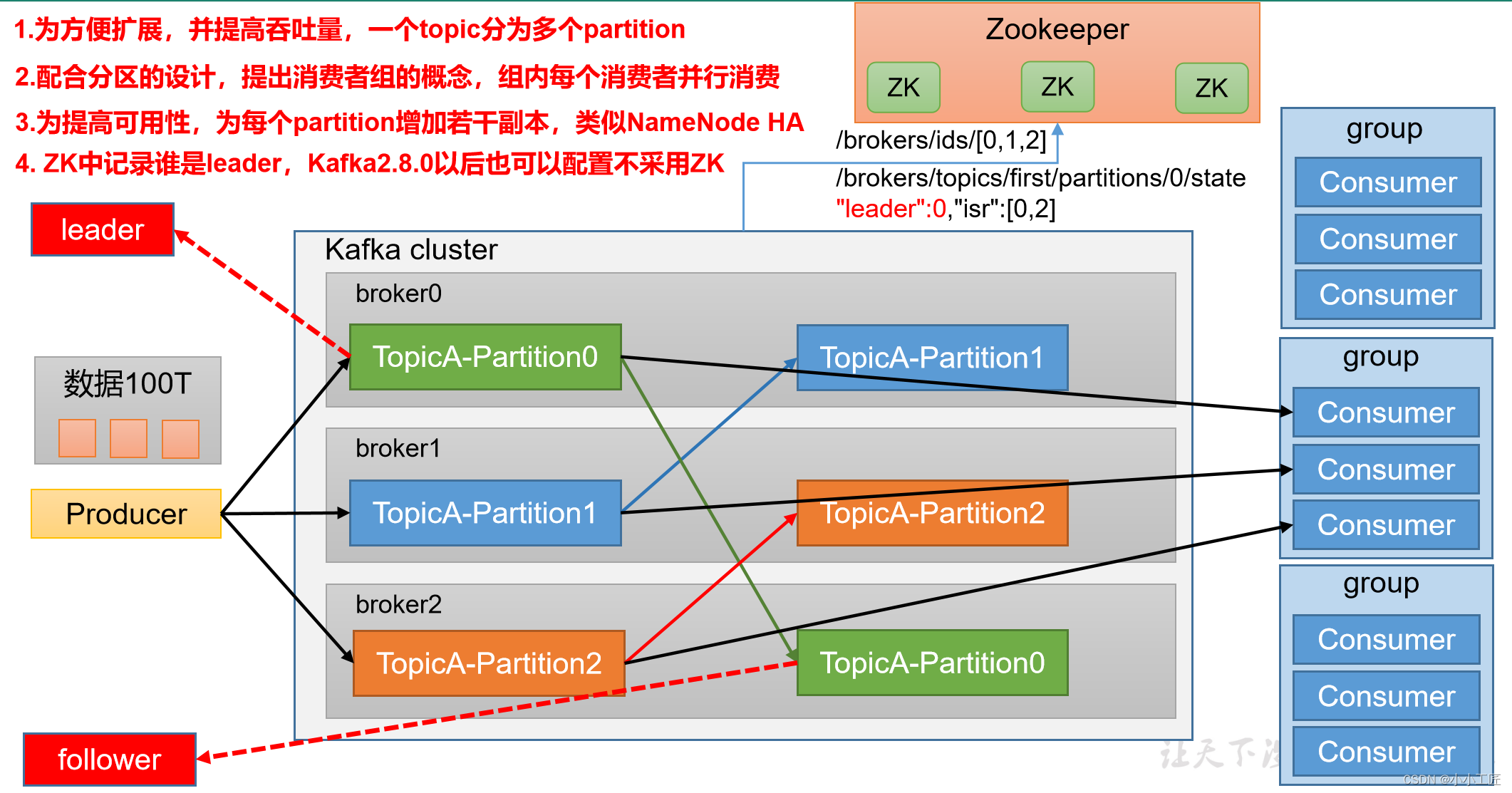
Kafka - 深入了解Kafka基础架构:Kafka的基本概念
文章目录 Kafka的基本概念 Kafka的基本概念 我们首先了解一些Kafka的基本概念。 1)Producer :消息生产者,就是向kafka broker发消息的客户端2)Consumer :消息消费者,向kafka broker获取消息的客户端3&…...
[Docker]二.Docker 镜像,仓库,容器介绍以及详解
一.Docker 镜像,容器,仓库的简单介绍 通俗来讲:镜像相当于VM虚拟机中的ios文件,容器相当于虚拟机系统,仓库相当于系统中的进程或者执行文件,容器是通过镜像创建的 1.镜像 Docker 镜像就是一个 Linux 的文件系统( Root FileSystem ),这个文…...

软考高级系统架构设计师系列之:案例分析典型试题一
软考高级系统架构设计师系列之:案例分析典型试题一 一、案例分析考试大纲二、结构化软件系统建模1.案例试题2.案例试题分析3.案例试题参考答案三、联合需求分析会议1.案例试题2.案例试题分析3.案例试题参考答案四、电子政务1.案例试题2.案例试题分析3.案例试题参考答案五、软件…...

2023年5个美国代理IP推荐,最佳代理花落谁家?
美国代理IP指的是代理服务器位于美国的IP地址,对于跨境业务来说,这些代理IP地址可以用于隐藏用户的真实IP地址,将其网络流量路由通过美国的服务器,以实现一些特定的目的。由于近年来,面向美国市场的跨境商家越来越多&a…...

github.com/holiman/uint256 源码阅读
github.com/holiman/uint256 源码阅读 // uint256: Fixed size 256-bit math library // Copyright 2018-2020 uint256 Authors // SPDX-License-Identifier: BSD-3-Clause// Package math provides integer math utilities.package uint256import ("encoding/binary&…...
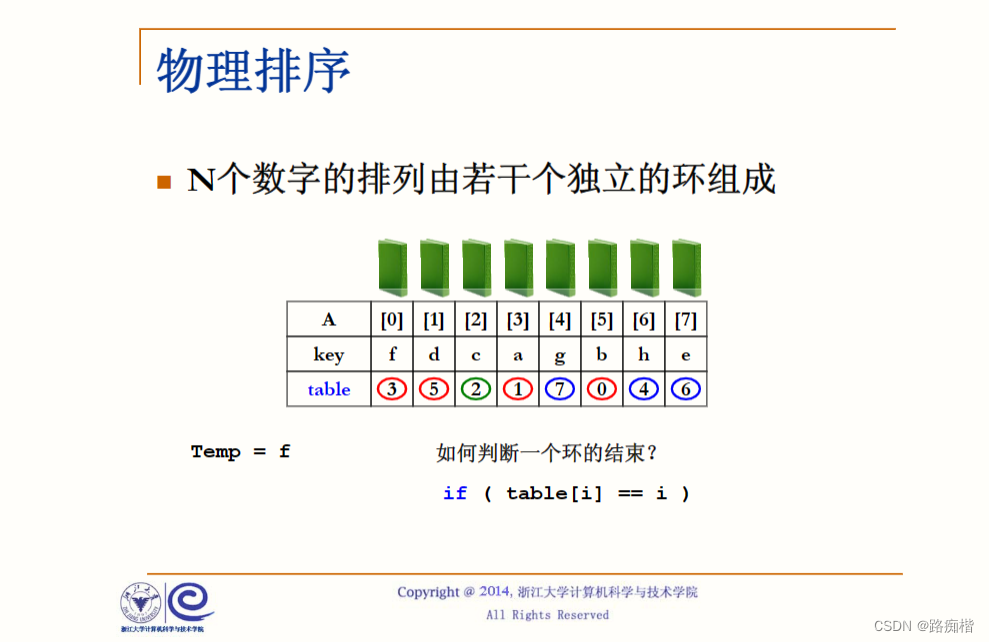
排序-表排序
当我们需要对一个很大的结构体进行排序时,因为正常的排序需要大量的交换,这就会造成时间复杂度的浪费 因此,我们引入指针,通过指针临时变量的方式来避免时间复杂度的浪费 间接排序-排序思路:通过开辟一个指针数组&…...

勒索病毒最新变种.locked1勒索病毒来袭,如何恢复受感染的数据?
引言: 在当今数字化时代,网络威胁不断进化,.locked1勒索病毒就是其中一种常见的恶意软件。这种病毒会加密您的文件,然后勒索赎金以解锁它们。本文将详细介绍.locked1勒索病毒,包括如何恢复被加密的数据文件和如何预防…...
信号补零对信号频谱的影响
文章目录 前言一、 什么是补零二、案例三、补零前仿真及分析1、补零前 MATLAB 源码2、仿真及结果分析①、 x n x_n xn 时域图②、 x n x_n xn 频谱图 四、补零后仿真及分析1、补6000个零且1000采样点①、 MATLAB 源码②、仿真及结果分析 2、波形分辨率3、补6000个零且7000采…...
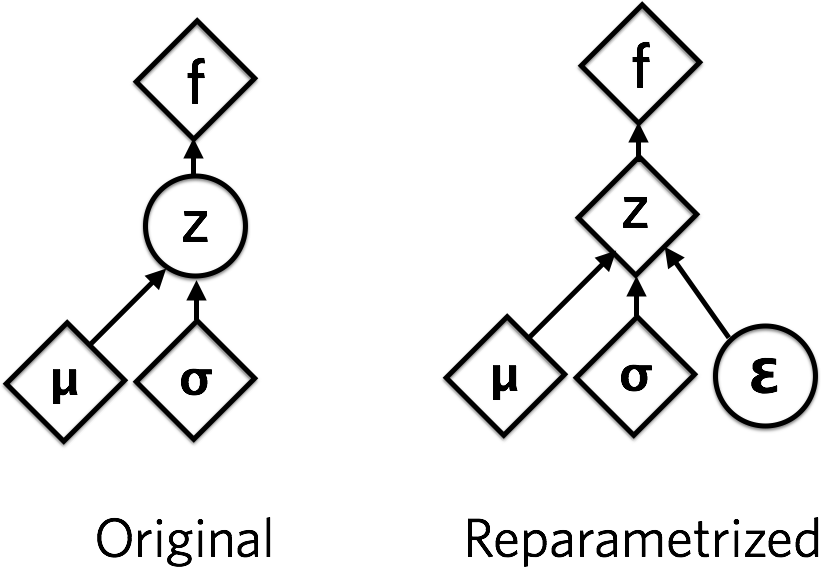
【Gan教程 】 什么是变分自动编码器VAE?
名词解释:Variational Autoencoder(VAE) 一、说明 为什么深度学习研究人员和概率机器学习人员在讨论变分自动编码器时会感到困惑?什么是变分自动编码器?为什么围绕这个术语存在不合理的混淆?本文从两个角度…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
