信号补零对信号频谱的影响
文章目录
- 前言
- 一、 什么是补零
- 二、案例
- 三、补零前仿真及分析
- 1、补零前 MATLAB 源码
- 2、仿真及结果分析
- 四、补零后仿真及分析
- 1、补6000个零且1000采样点
- ①、 MATLAB 源码
- ②、仿真及结果分析
- 2、波形分辨率
- 3、补6000个零且7000采样点
- ①、 MATLAB 源码
- ②、仿真及结果分析
- 4、补7000个零且7000采样点
- ①、 MATLAB 源码
- ②、仿真及结果分析
- 五、补零的好处
- 六、资源自取
前言
本文对信号补零前与补零后分别做 FFT,对频谱进行分析。
先抛出结论:
补 1 次零相当于在原始频谱图中每两个频率之间插入1个频率值,补 2 次零相当于在原始频谱图中每两个频率之间插入 2 个频率值,并且原始频率值的位置及其幅值保持不变。因此, 补零会使频谱图中的频率点的数量增加,从而使得频谱图更加的光滑连续,但是补零不能对频谱图中的频率分辨率、频率值以及幅值有所改善。
一、 什么是补零
FFT 运算点数( M M M) > 采样点数( N N N)时, f f t ( x n , M ) fft(xn,M) fft(xn,M) 函数对信号 x n x_n xn 进行尾补零操作即在该信号尾部添加多个值为 0 的数据点以使信号总点数 N N N 增至 FFT 运算所需点数 M M M。
二、案例
目前有一个信号 ,这个信号中仅包含两个正(余)弦波,一个是 1 M H z 1MHz 1MHz,一个是 1.5 M H z 1.5MHz 1.5MHz,即 x = c o s ( 2 π ∗ 1000000 t ) + c o s ( 2 π ∗ 1050000 t ) x=cos(2\pi*1000000t)+cos(2\pi*1050000t) x=cos(2π∗1000000t)+cos(2π∗1050000t)。设定采样频率为 F s = 100 M H z F_s=100MHz Fs=100MHz,如果采 1000 个点,那么时域信号的时长就有 10 μ s 10\mu s 10μs。(采样率*采样时间=采样点数)
三、补零前仿真及分析
直接对这 1000 个数据点做 FFT
1、补零前 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 1000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [未补零 被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [未补零 被采信号 && 绘制频谱图]
M = 1000; % FFT 运算点数
X = fft(xn, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('xn 频谱图');
ylabel('X(f)');
xlabel('频率/Hz');
2、仿真及结果分析
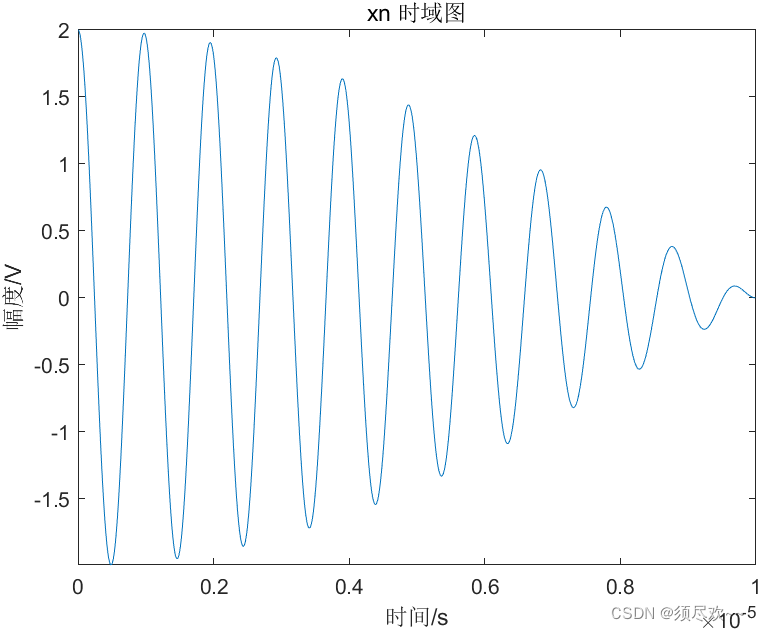
①、 x n x_n xn 时域图
②、 x n x_n xn 频谱图
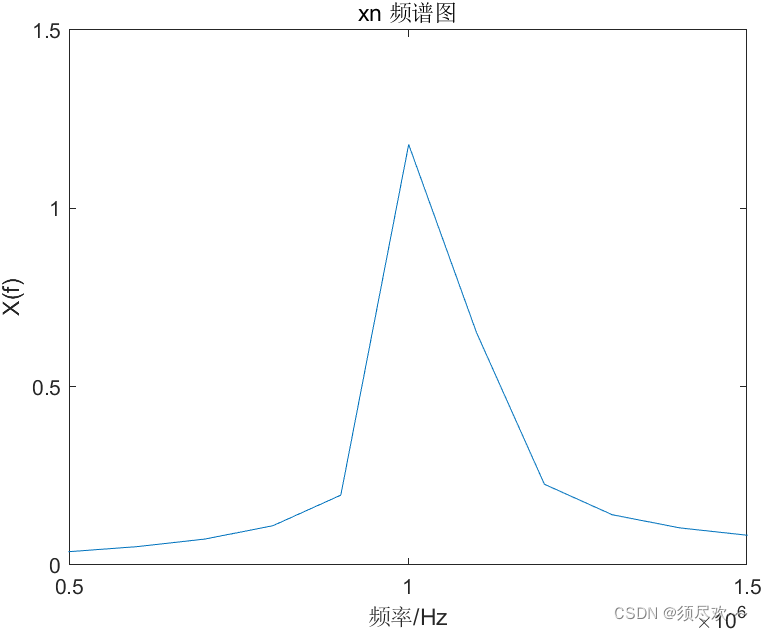
如上图所示,直接对这 1000 个数据点做快速傅里叶变换,将得到频谱,只有一个谱峰,在 1 M H z 1MHz 1MHz 的地方,由于频谱点稀疏,在 1 M H z 1MHz 1MHz 根本无法将 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 的两个频率分开,这是因为频率分辨率不够,采样率 100 M H z 100MHz 100MHz,FFT 点数 1000 个点,频率分辨率 = 采样率 /FFT 点数 = 100 K H z 100 KHz 100KHz,所以无法区分 50 K H z 50KHz 50KHz。
四、补零后仿真及分析
对数据补零,增加 FFT 点数,比如补 6000 个零,做 7000 个点的 FFT。
1、补6000个零且1000采样点
①、 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 1000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [尾补零 被采信号 && 绘制时域波形]
xnwei=[xn zeros(1,6000)]; % 补6000个零
M = length(xnwei); % FFT 运算点数
X = fft(xnwei, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('补零后共7000个数据点做FFT的频谱');
ylabel('X(f)');
xlabel('频率/Hz');
②、仿真及结果分析
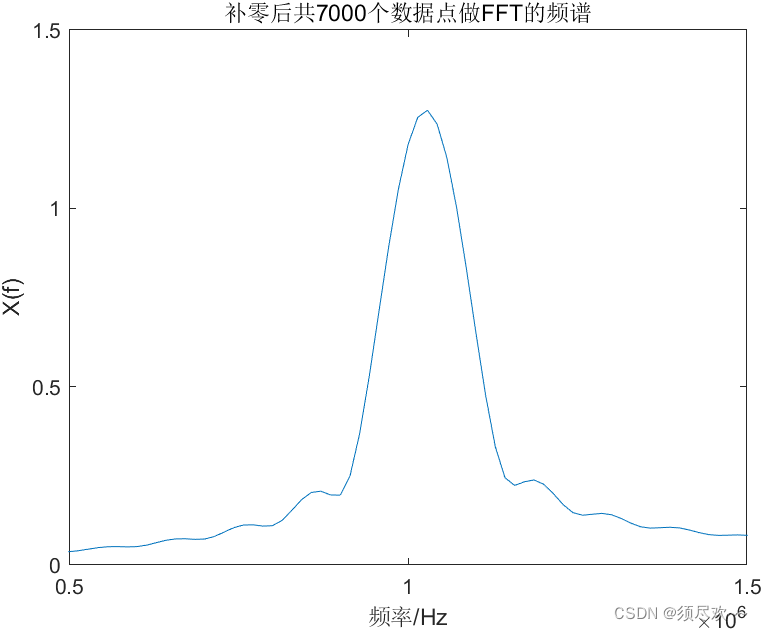
可以看到信号频谱变得平滑了,但是仍然无法区分 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz
这里就要引出一个波形分辨率的概念,虽然补零了,提高了频谱分辨率,但是无法提高波形分辨率
2、波形分辨率
发现频率成分无法被区分开,第一反应就是:频率分辨率不够,那么,如何提高频率分辨率呢?首先要清楚,这里存在两种类型的频率分辨率。
一种叫波形分辨率,其由原始数据的时间长度决定:
Δ R w = 1 T \Delta R_w=\frac{1}{T} ΔRw=T1
另一种可以称之为视觉分辨率或FFT分辨率,其由采样频率和参与 FFT 的数据点数决定:
Δ R f f t = F s N f f t \Delta R_{fft}=\frac{F_s}{N_{fft}} ΔRfft=NfftFs
之所以要区分,就是因为后面要进行 “补零” 操作。如果不补零,直接对原始数据做 FFT,那么这两种分辨率是相等的。
例如上面,有:
Δ R w = 1 10 μ s = Δ R f f t = 100 M H z 1000 = 100 K H z \Delta R_w=\frac{1}{10\mu s}=\Delta R_{fft}=\frac{100MHz}{1000}=100KHz ΔRw=10μs1=ΔRfft=1000100MHz=100KHz
所以要想提高波形分辨率,必须提高信号数据本身的长度
3、补6000个零且7000采样点
采样 7000 个信号数据做 FFT,还是补 6000 个零 ,做 7000 个点的 FFT
①、 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 7000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [尾补零 被采信号 && 绘制时域波形]
xnwei=[xn zeros(1,6000)]; % 补6000个零
M = length(xnwei); % FFT 运算点数
X = fft(xnwei, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('采样点7000且补零后共7000个数据点做FFT的频谱');
ylabel('X(f)');
xlabel('频率/Hz');
②、仿真及结果分析
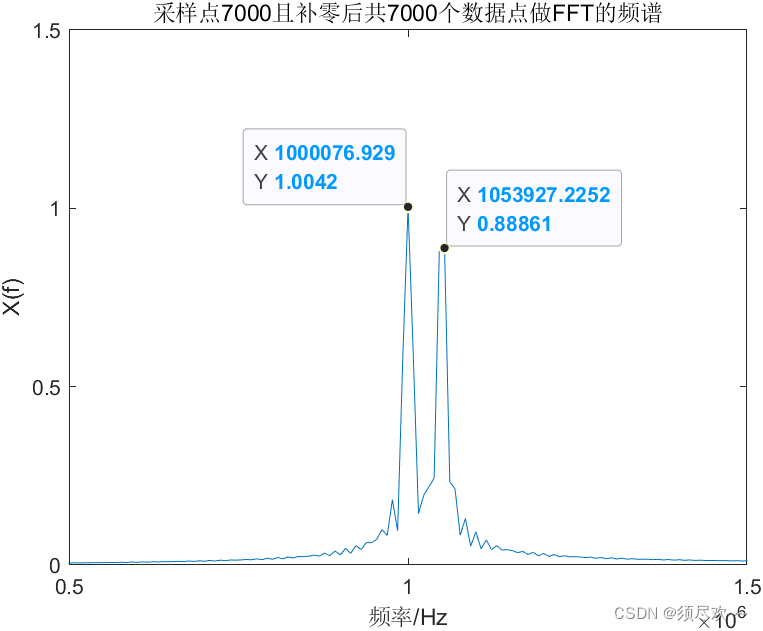
因为此时的波形分辨率为: Δ R w = 1 70 μ s ≈ 14 K H z \Delta R_w=\frac{1}{70 \mu s}\approx14KHz ΔRw=70μs1≈14KHz,小于 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 这两个频率成分之间的举例 50 K H z 50KHz 50KHz,所以可以看出有两个明显的峰值。
但是会发现 1 M H z 1MHz 1MHz 对应的幅值为 1,与原始信号中该频率成分的幅值一致,但是 1.05 M H z 1.05MHz 1.05MHz 对应的幅值明显低于 1,但是其周边的点上确有不小的幅值,这就是所谓的频谱泄露,因为数据点的个数影响,使得在 1 M H z 1MHz 1MHz 处有谱线存在,但在 1.05 M H z 1.05MHz 1.05MHz 处没有谱线存在,使测量结果偏离实际值,同时在实际频率点的能量分散到两侧的其他频率点上,并出现一些幅值较小的假谱。
这是因为在 1.05 M H z 1.05MHz 1.05MHz 那个地方刚好有个频点,也就是出现了所谓的频谱泄漏,还是数据长度不够,但这时是可以通过补零来达到目的。补零 1000 个点,做 8000 点的FFT。
4、补7000个零且7000采样点
采样 7000 个信号数据做 FFT,补 7000 个零 ,做 8000 点的 FFT
①、 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 7000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [尾补零 被采信号 && 绘制时域波形]
xnwei=[xn zeros(1,7000)]; % 补7000个零
M = length(xnwei); % FFT 运算点数
X = fft(xnwei, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('采样点7000且补零后共8000个数据点做FFT的频谱');
ylabel('X(f)');
xlabel('频率/Hz');
②、仿真及结果分析

FFT 分辨率为 F s / N = 100 M H z / 8000 = 12.5 K H z F_s/ N=100MHz/8000=12.5KHz Fs/N=100MHz/8000=12.5KHz,是这两个频率的公约数, 1 M H z = 80 ∗ 12.5 K H z 1MHz = 80*12.5KHz 1MHz=80∗12.5KHz, 1.05 M H z = 84 ∗ 12.5 K H z 1.05MHz=84*12.5KHz 1.05MHz=84∗12.5KHz,所以谱线同时经过 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 这两个点。
从上图也可以看到效果也比较理想,将 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 的两个信号频率分开。
五、补零的好处
- 使数据 N 为 2 的整次幂,便于使用 FFT
- 补零后,其实是对 DFT 结果做了插值,克服“栅栏"效应,使谱外观平滑化。我把“栅栏"效应形象理解为,就像站在栅栏旁边透过栅栏看外面风景,栅栏会挡住比较多风景,此时就可能漏掉较大频域分量,但是补零以后,相当于你站远了,风景就看的越来越清楚了。
- 由于对时域数据的截短必然造成频谱泄露,因此在频谱中可能出现难以辨认的谱峰,补零在一定程度上能消除这种现象。
对信号进行头补零或尾补零再得到的幅频响应相等,相频响应不同
补零会使频谱图中的频率点的数量增加,从而使得频谱图更加的光滑连续,但是补零不能对频谱图中的频率分辨率、频率值以及幅值有所改善。
- 补零(Zero-padding)是在FFT计算中向输入信号序列的末尾添加零值,从而增加信号的长度。这样做的主要目的是在频域中插入更多的零频率样本,以获得更好的频谱分析图。
- 补零可以在一定程度上改善频谱图的可视化效果,使频谱图在频率轴上呈现更平滑的外观。这是因为补零增加了离散傅里叶变换(DFT)点数,从而在频率轴上产生更多的插值点。然而,这并不意味着补零改善了频率分辨率或精确性。
- 频率分辨率由采样率和FFT长度决定,而补零并不改变采样率。补零只是对现有的采样点进行插值,不会增加频率分辨率。实际上,补零只是在现有的频率分辨率上插入了更多的点,而不是提高了分辨率本身。
- 频率值和幅值也不会因为补零而改变。补零只是在现有的频率轴上插入了更多的点,对原有的频率值和幅值进行了插值。这些插值点的值是通过对原始采样点进行插值计算得到的,而不是通过补零本身引入的信息。
- 如果希望改善频率分辨率或精确性,需要增加采样率或使用更长的FFT长度。
六、资源自取
信号补零对信号频谱的影响
我的qq:2442391036,欢迎交流!
相关文章:

信号补零对信号频谱的影响
文章目录 前言一、 什么是补零二、案例三、补零前仿真及分析1、补零前 MATLAB 源码2、仿真及结果分析①、 x n x_n xn 时域图②、 x n x_n xn 频谱图 四、补零后仿真及分析1、补6000个零且1000采样点①、 MATLAB 源码②、仿真及结果分析 2、波形分辨率3、补6000个零且7000采…...
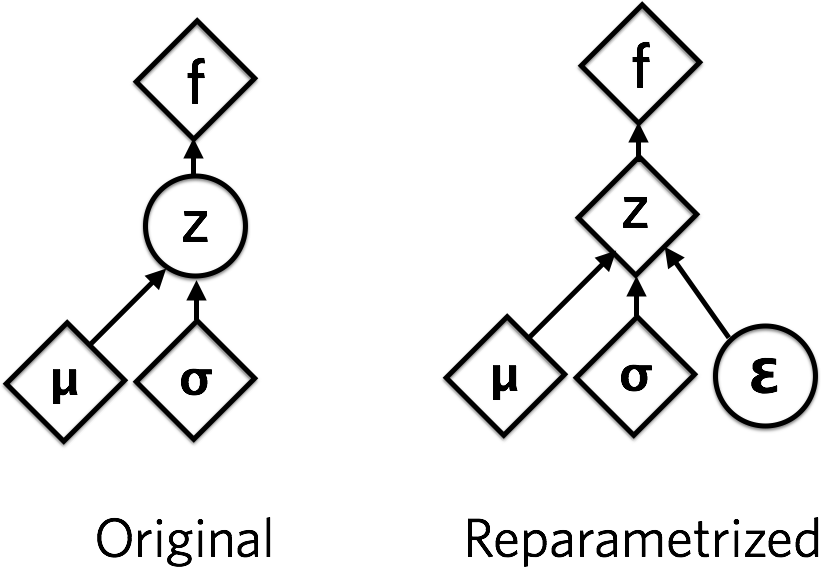
【Gan教程 】 什么是变分自动编码器VAE?
名词解释:Variational Autoencoder(VAE) 一、说明 为什么深度学习研究人员和概率机器学习人员在讨论变分自动编码器时会感到困惑?什么是变分自动编码器?为什么围绕这个术语存在不合理的混淆?本文从两个角度…...
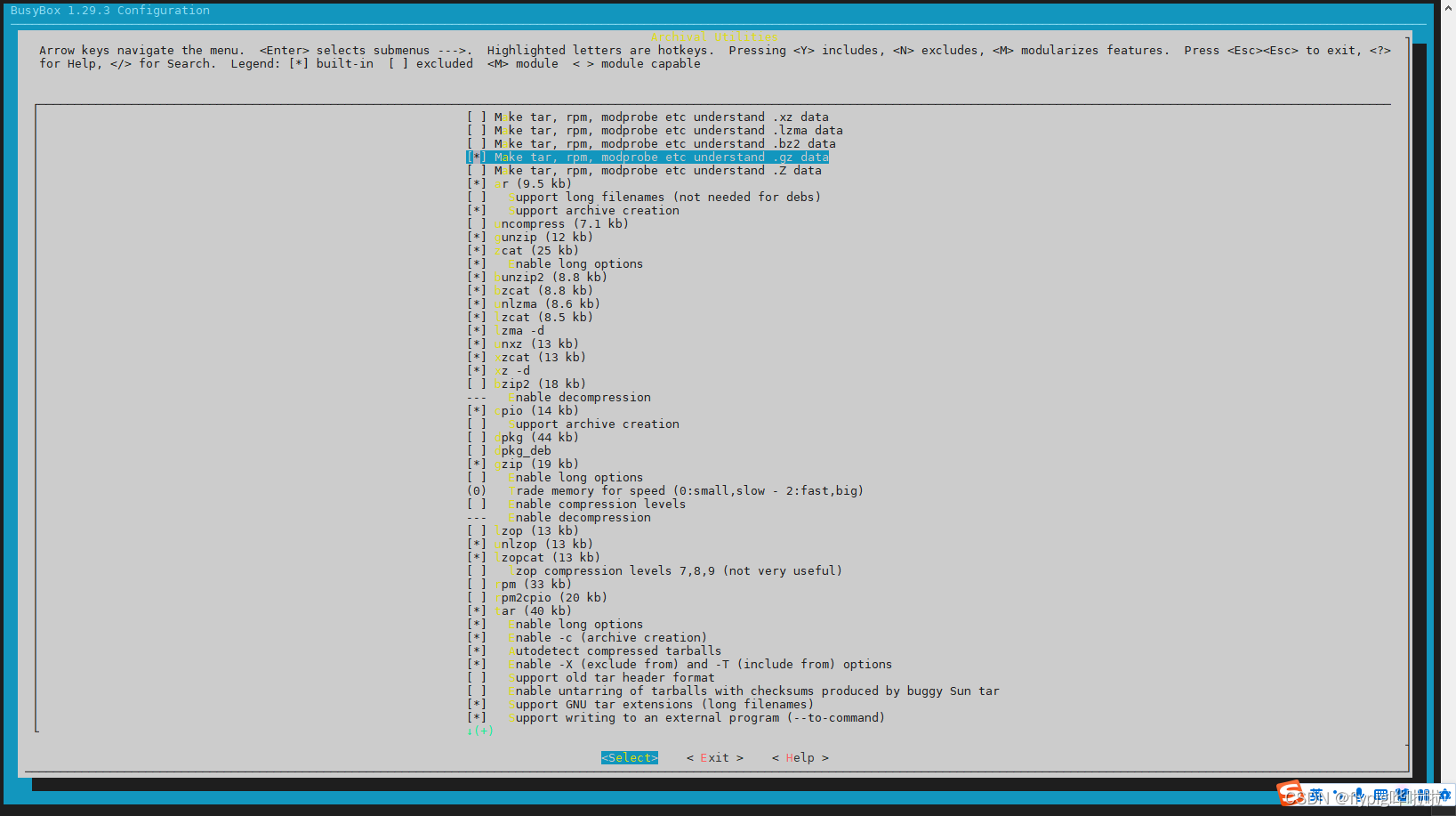
T113-S3-buildroot文件系统tar解压缩gz文件
目录 前言 一、现象描述 二、解决方案 三、tar解压缩.gz文件 总结 前言 本文主要介绍全志T113-S3平台官方SDK,buildroot文件系统tar不支持.gz文件解压缩的问题以及如何配置buildroot文件系统解决该问题的方法介绍。 一、现象描述 在buildroot文件系统中ÿ…...

软件测试面试题:压测时,QPS一直上不去,如何排查?
在进行系统压测时,QPS(Queries Per Second)即每秒查询数,无法达到预期值是一个常见的问题,本文就来介绍下QPS一直上不去时应该如何排查。 一. 检查硬件资源 CPU使用率 使用top或nmon命令来查看CPU使用率。如果CPU使…...

探索JavaScript ES6+新特性
JavaScript是一门十分流行的编程语言,它不断发展演变以适应现代Web开发需求。ES6(也称为ECMAScript 2015)是JavaScript的第六个版本,引入了许多令人兴奋的新特性和语法糖。本文将介绍一些ES6中最有趣和实用的特性。 箭头函数 箭…...

Elasticsearch常见错误
一 read_only_allow_delete" : "true" 当我们在向某个索引添加一条数据的时候,可能(极少情况)会碰到下面的报错: {"error": { "root_cause": [ { "type": "cluster_block_exception", "r…...

mysql源码编译安装
下载地址:http://dev.mysql.com/downloads/mysql/5.1.html#downloads 免费版,只能下载mysql社区版。MySQL Community Server 选择合适的版本迚行下载: 安装前,如果不存在mysql 用户,则建立之 [rootlocalhost ~]# useradd mys…...
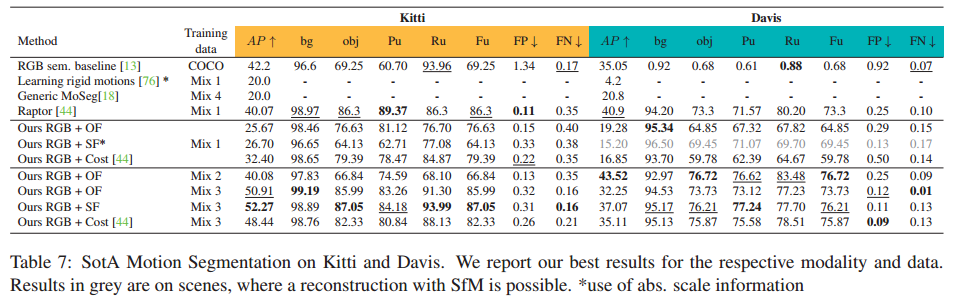
On Moving Object Segmentation from Monocular Video with Transformers 论文阅读
论文信息 标题:On Moving Object Segmentation from Monocular Video with Transformers 作者: 来源:ICCV 时间:2023 代码地址:暂无 Abstract 通过单个移动摄像机进行移动对象检测和分割是一项具有挑战性的任务&am…...

[AutoSar NVM] 存储架构
依AutoSAR及公开知识辛苦整理,禁止转载。 专栏 《深入浅出AutoSAR》, 全文 2900 字. 图片来源: 知乎 汽车的ECU内存中有很多不同类型的变量,这些变量包括了车辆各个系统和功能所需的数据。大部分变量在ECU掉电后就会丢失&#x…...

ES10 新特性
1. Object.fromEntries Object.fromEntries() 方法把可迭代对象的键值对列表转换为一个对象。 语法: Object.fromEntries(iterable)iterable:类似 Array 、 Map 或者其它实现了可迭代协议的可迭代对象。返回值:一个由该迭代对象条目提供对应属性的新对象。相当于 Object.e…...

宝塔安装脚本
Centos安装脚本 yum install -y wget && wget -O install.sh https://download.bt.cn/install/install_6.0.sh && sh install.sh ed8484bec Ubuntu/Deepin安装脚本 wget -O install.sh https://download.bt.cn/install/install-ubuntu_6.0.sh && sud…...
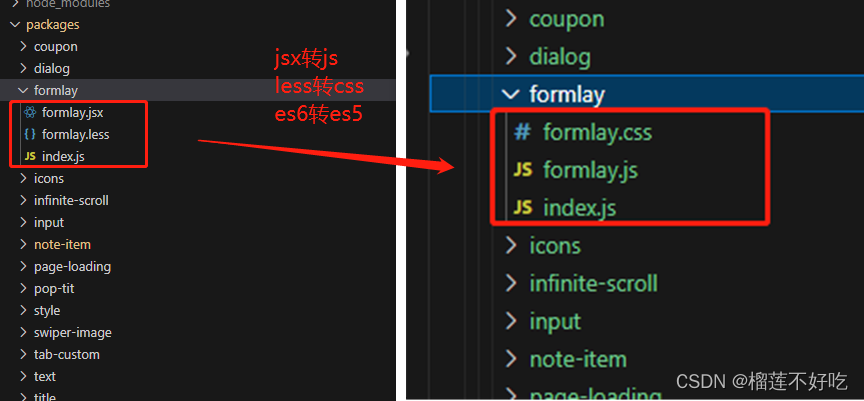
gulp打包vue3+jsx+less插件
最终转换结果如下 在根目录下添加gulpfile.js文件,package.json添加命令npm run gulp var gulp require(gulp) var babel require(gulp-babel) var less require(gulp-less) var del require(del); var spawn require(child_process).spawn;const outDir &…...

华为ICT——第四章深度学习和积卷神经
接第三章的末尾: 目录 接第三章的末尾: 1:自适应阈值分割: 2:形态处理: 4:膨胀: 5:腐蚀 6:开运算 7:闭运算 8:特征描述子 9…...
)
MongoDB 学习笔记(基础)
概论 出现背景:MongoDB 是文档型数据库,由于传统的关系型数据库(如 MySQL),在数据操作的“三高”需求以及应对 web 的网站需求面前显得有些吃力,在此环境下 MongoDB 出世了 三高需求: (1) 对数…...

【TGRS 2023】RingMo: A Remote Sensing Foundation ModelWith Masked Image Modeling
RingMo: A Remote Sensing Foundation Model With Masked Image Modeling, TGRS 2023 论文:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber9844015 代码:https://github.com/comeony/RingMo MindSpore/RingMo-Framework (gitee.com) …...

性能测试 —— 生成html测试报告、参数化、jvm监控
1.生成HTML的测试报告 1.1配置 (1)找到jmeter 的安装目录,下的bin中的jmeter.properties(jmeter配置文件) (2) ctrl f ,搜索jmeter.save.saveservice.output_format,取消井号 并且 把等号后的xml改为csv,…...
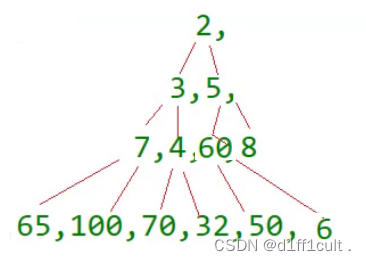
堆(二叉树,带图详解)
一.堆 1.堆的概念 2.堆的存储方式 逻辑结构 物理结构 2.堆的插入问题 3.堆的基本实现(代码)(以小堆为例) 1.堆的初始化 2. 向上调整 3.插入结点 4. 交换函数、堆的打印 5.向下调整 6.删除根节点并调整成小根堆 7.获取堆…...
vue3 code format bug
vue code format bug vue客户端代码格式化缺陷,为了方便阅读和维护,对代码格式化发现这个缺陷 vue.global.min.3.2.26.js var Vuefunction(r){"use strict";function e(e,t){const nObject.create(null);var re.split(",");for(le…...

7-3、S曲线生成器【51单片机控制步进电机-TB6600系列】
摘要:本节介绍步进电机S曲线生成器的计算以及使用 一.计算原理 根据上一节内容,已经计算了一条任意S曲线的函数。在步进电机S曲线加减速的控制中,需要的S曲线如图1所示,横轴为时间,纵轴为角速度,其中w0为起…...
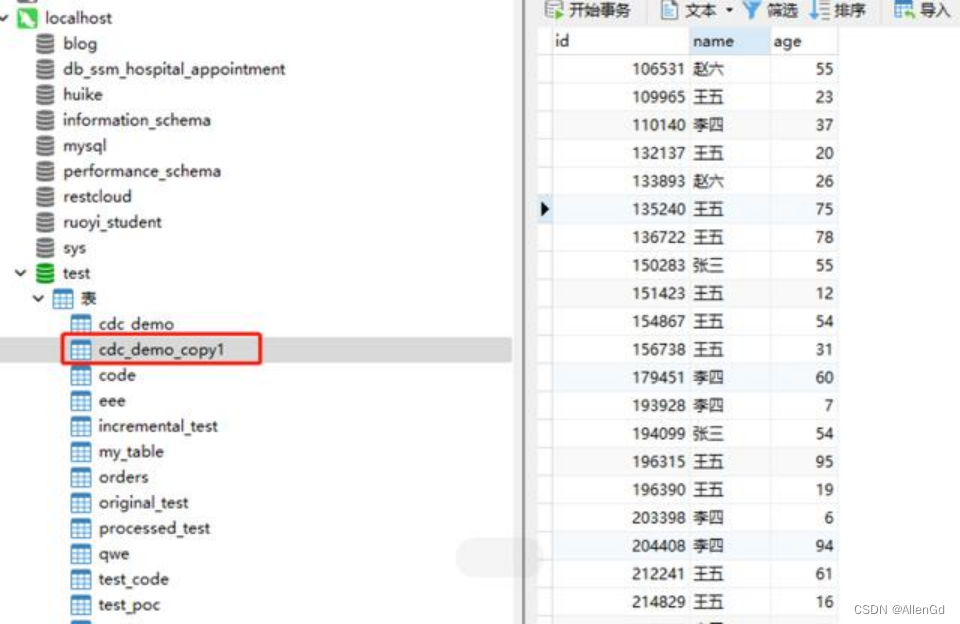
CDC实时数据同步
一丶CDC实时数据同步介绍 CDC实时数据同步指的是Change Data Capture(数据变更捕获)技术在数据同步过程中的应用。CDC技术允许在数据源发生变化时,实时地捕获这些变化,并将其应用到目标系统中,从而保持数据的同步性。…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
