自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例
自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例
在matlab中有自带的离散傅里叶变换程序,即fft程序,但该程序是封装的,无法看到源码。为了比较清楚的了解matlab自带的实现过程,本文通过自建程序实现matlab程序,并与matlab自带的fft进行比较计算。
一、离散傅里叶变换的计算公式
在计算离散傅里叶变换的时候,通常会用到:
{ X ( k ) = ∑ n = 1 N [ x ( n ) ⋅ exp ( − i ⋅ 2 π ( k − 1 ) ( n − 1 ) N ) ] s . t . { 1 ≤ k ≤ N } (1) \left\{ \begin{array}{l}X(k) = \sum\limits_{n = 1}^N {[x(n) \cdot \exp ( - i \cdot 2\pi \frac{{(k - 1)(n - 1)}}{N})]} \\s.t.\{ 1 \le k \le N\} \end{array} \right. \tag1 ⎩ ⎨ ⎧X(k)=n=1∑N[x(n)⋅exp(−i⋅2πN(k−1)(n−1))]s.t.{1≤k≤N}(1)进行求解。
但有时会遇到所求解的向量长度N和变换过程中的长度K,大小不同。此时,会遇到 N ≤ K N\le K N≤K的情况,和N>K的两种情况。
(1) 当 N ≤ K N\le K N≤K时,则需要对向量 x x x补零后,再离散傅里叶变换计算。计算公式为:
{ X ( k ) = ∑ n = 1 N p a d d e d [ x ( n ) ⋅ exp ( − i ⋅ 2 π ( k − 1 ) ( n − 1 ) N p a d d e d ) ] s . t . { 1 ≤ k ≤ N p a d d e d } (2) \left\{ \begin{array}{l}X(k) = \sum\limits_{n = 1}^{{N_{padded}}} {[x(n) \cdot \exp ( - i \cdot 2\pi \frac{{(k - 1)(n - 1)}}{{{N_{padded}}}})]} \\s.t.\{ 1 \le k \le {N_{padded}}\} \end{array} \right. \tag2 ⎩ ⎨ ⎧X(k)=n=1∑Npadded[x(n)⋅exp(−i⋅2πNpadded(k−1)(n−1))]s.t.{1≤k≤Npadded}(2)
易知: N ≤ N p a d d e d = K N \le {N_{padded}}=K N≤Npadded=K.
(2) 当N>K时,,则需要对向量 x x x截断后,再离散傅里叶变换计算。计算公式为:
{ X ( k ) = ∑ n = 1 N t r u n c a t e d [ x ( n ) ⋅ exp ( − i ⋅ 2 π ( k − 1 ) ( n − 1 ) N t r u n c a t e d ) ] s . t . { 1 ≤ k ≤ N t r u n c a t e d } (3) \left\{ \begin{array}{l}X(k) = \sum\limits_{n = 1}^{{N_{truncated}}} {[x(n) \cdot \exp ( - i \cdot 2\pi \frac{{(k - 1)(n - 1)}}{{{N_{truncated}}}})]} \\s.t.\{ 1 \le k \le {N_{truncated}}\} \end{array} \right. \tag3 ⎩ ⎨ ⎧X(k)=n=1∑Ntruncated[x(n)⋅exp(−i⋅2πNtruncated(k−1)(n−1))]s.t.{1≤k≤Ntruncated}(3)
易知: N > N t r u n c a t e d = K N > {N_{truncated}}=K N>Ntruncated=K.
二、基于上述理论编写myfft函数(matlab编程)
将自建的离散傅里叶变换的函数命名为myfft,编写程序如下:
function X=myfft(x,K)
% myfft函数根据傅里叶变换公式编写的离散傅里叶变换程序
% 输入
% x:向量x
% K: 变换后的向量X的长度% 输出
% X: 经过傅里叶变换得到的向量% 变换依据:
% 对于长度为N的输入向量x,其离散傅里叶变换是长度为N的向量X,其具有元素:
% N
% X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N.
% n=1
% myfft(x,K) 是一个K点的FFT,如果x小于K点,则补零后进行傅里叶变换;如果x大于K点,则截断后傅里叶变换。% by zddh and zsm
% 2023.10.24N=length(x)%% 1.如果x小于K点,补零运算
if N<=Kx_padded=[x,zeros(1,K-N)]; %补零N_padded=length(x_padded); %补零后的长度X=zeros(1,N_padded);
for k=1:Kfor n=1:N_paddedtemp1=x_padded(n)*exp(-i*2*pi*(k-1)*(n-1)/N_padded);X(k)=X(k)+temp1;end
end
%% 2.如果x大于K点,则截断计算
elsewarning('K值小于N,则截断后进行傅里叶变换')
x_truncated=x(1:K);
N_truncated=length(x_truncated);
X=zeros(1,N_truncated)
for k=1:Kfor n=1:N_truncatedtemp2=x_truncated(n)*exp(-i*2*pi*(k-1)*(n-1)/N_truncated);X(k)=X(k)+temp2;end
end
end三、自建的函数和matlab自带函数比较举例
(1) 编写程序
clc
clear all
close all
%% 1.构造将要变换的向量
dt=0.1
t=0:dt:10*pi;
x=sin(t)
N=length(x);
figure(1)
plot(t,x,'lineWidth',2)%% 2.自建的离散傅里叶变换求解
K=200
X=myfft(x,K)
%% 3.matlab自带函数求解
X0=fft(x,K)%% 4.比较
D_value=X-X0;figure(2)
subplot(211)
plot(abs(X),'LineWidth',2)
hold on
plot(abs(X0),'LineWidth',2)
legend('myfft','matlabfft')
title('自建myfft和matlab自带函数fft比较')subplot(212)
plot(abs(D_value),'LineWidth',2)
title('|X-X0|')
(2)运行结果
图1 生成的x向量
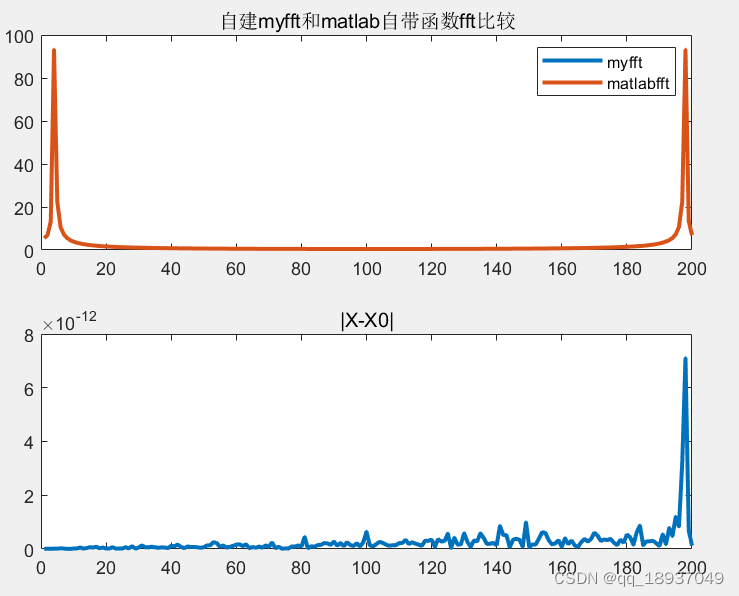
图2 使用两种方法结果
通过对图2两个子图观察比较可知,本文所编写的myfft函数和matlab自带的fft函数之间的误差非常小,在 1 0 − 12 10^{-12} 10−12量级,同时验证了程序的理论公式(1)、(2)和(3).
相关文章:

自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例
自建的离散傅里叶变换matlab程序实现及其与matlab自带函数比较举例 在matlab中有自带的离散傅里叶变换程序,即fft程序,但该程序是封装的,无法看到源码。为了比较清楚的了解matlab自带的实现过程,本文通过自建程序实现matlab程序&…...

Vue图片路径问题(动态引入)
vue项目中我们经常会遇到动态路径的图片无法显示的问题,以下是静态路径和动态路径的常见使用方法。 1.静态路径 在日常的开发中,图片的静态路径通过相对路径和绝对路径的方式引入。 相对路径:以.开头的,例如./、../之类的。就是…...
项目部署Linux步骤
1、最小化安装centos7-环境准备 安装epel-release 安装epel-release,因为有些rpm包在官方库中找不到。前提是保证可以联网 yum install -y epel-release 修改IP net-tools net-tool:工具包集合,包含ifconfig等命令 yum install -y net-…...
UG\NX二次开发 在资源栏(左侧面板)中添加按钮
文章作者:里海 来源网站:王牌飞行员_里海_里海NX二次开发3000例,里海BlockUI专栏,C\C++-CSDN博客 感谢粉丝订阅 感谢 apolloryd 订阅本专栏,非常感谢。 简介 UG\NX二次开发 在资源栏(左侧面板)中添加按钮,下面提供了帮助说明,在 UGOPEN 文件夹下有示例。 C++语言在UG二次…...

Proteus仿真--量程自动切换数字电压表(仿真+程序)
本文主要介绍基于51单片机的量程自动切换数字电压表Proteus仿真设计(完整仿真源文件及代码见文末链接) 简介 硬件电路主要分为单片机主控模块、AD转换模块、量程选择模块以及数码管显示模块 (1)单片机主控模块:单片…...
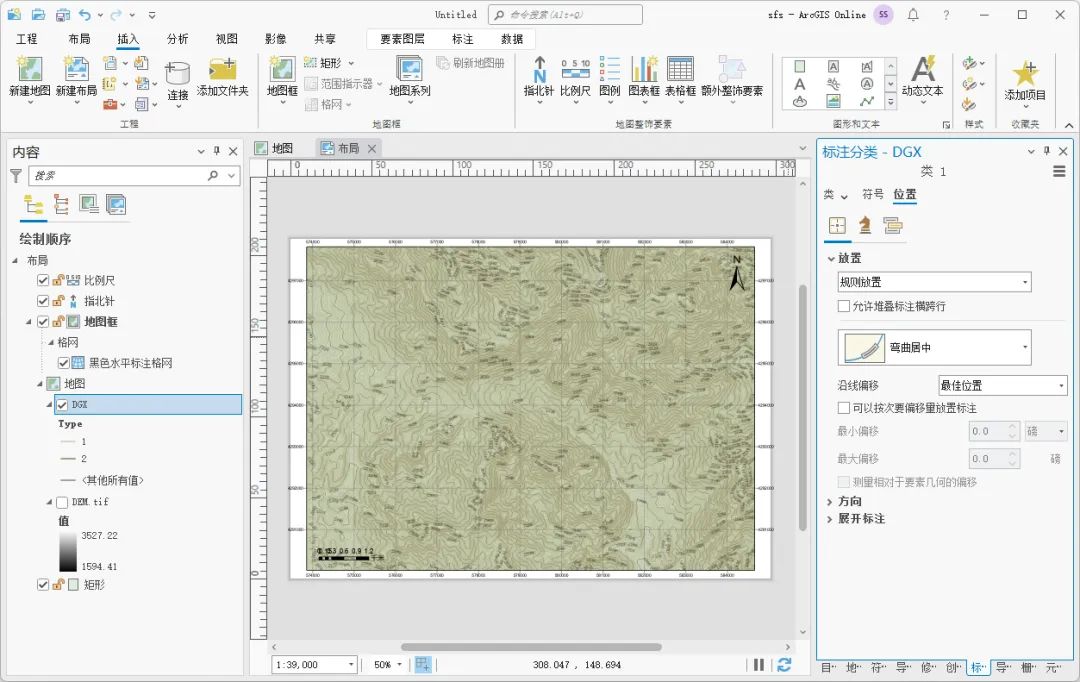
如何使用ArcGIS Pro制作一张地形图
01数据来源 本教程所使用的数据是从水经微图中下载的DEM数据,除了DEM数据,常见的GIS数据都可以从水经微图中下载,你可以通过关注“水经注GIS”,然后在后台回复“微图”即可获取软件下载地址,当然也可以直接在水经注…...

人工智能三要数之算法Transformer
1. 人工智能三要数之算法Transformer 人工智能的三个要素是算法、数据和计算资源。Transformer 模型作为一种机器学习算法,可以应用于人工智能系统中的数据处理和建模任务。 算法: Transformer 是一种基于自注意力机制的神经网络模型,用于处理序列数据的…...

Java ThreadPoolExecutor 线程池
import java.util.concurrent.ThreadPoolExecutor; import java.util.concurrent.TimeUnit; import java.util.concurrent.ArrayBlockingQueue;public class ThreadPoolExample {public static void main(String[] args) {// 创建线程池对象ThreadPoolExecutor threadPool new…...

网络协议--IP选路
9.1 引言 选路是IP最重要的功能之一。图9-1是IP层处理过程的简单流程。需要进行选路的数据报可以由本地主机产生,也可以由其他主机产生。在后一种情况下,主机必须配置成一个路由器,否则通过网络接口接收到的数据报,如果目的地址不…...
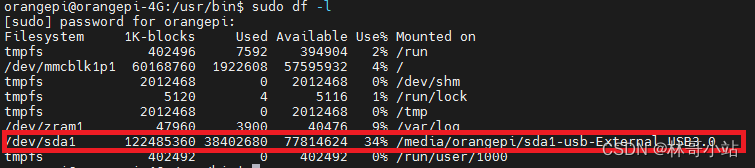
使用udevil自动挂载U盘或者USB移动硬盘
最近在折腾用树莓派(实际上是平替香橙派orangepi zero3)搭建共享文件服务器,有一个问题很重要,如何在系统启动时自动挂载USB移动硬盘。 1 使用/etc/fstab 最开始尝试了用/etc/fstab文件下增加:"/dev/sda1 /home/orangepi/s…...

学习笔记二十二:K8s控制器Replicaset
K8s控制器Replicaset Replicaset控制器:概念、原理解读Replicaset概述Replicaset工作原理:如何管理PodReplicaset控制器三个组成部分 Replicaset资源清单文件编写技巧Replicaset使用案例:部署Guestbook留言板编写一个ReplicaSet资源清单资源清…...

2023-10-25 精神分析-领悟新技术的错误做法-持续数年的错误做法-记录与分析
摘要: 过去数年对于领悟技术, 采取的做法不能说是对达到目的毫无裨益,但是对突破技术和将技术融为自身这个目的来说, 没有达到。 而且随着时间的流逝, 过去已经熟悉的技术, 竟然会被忘掉!就像是没有涉猎过一样! 根本原因出在对技术的领悟的…...
方法)
Arrays 中的 asList()方法
public static <T> List<T> asList( T . . . a ){ return new ArrayList<>(a); } 返回由指定数组支持的固定大小的 list集合。对数组所做的更改将在返回的 l…...
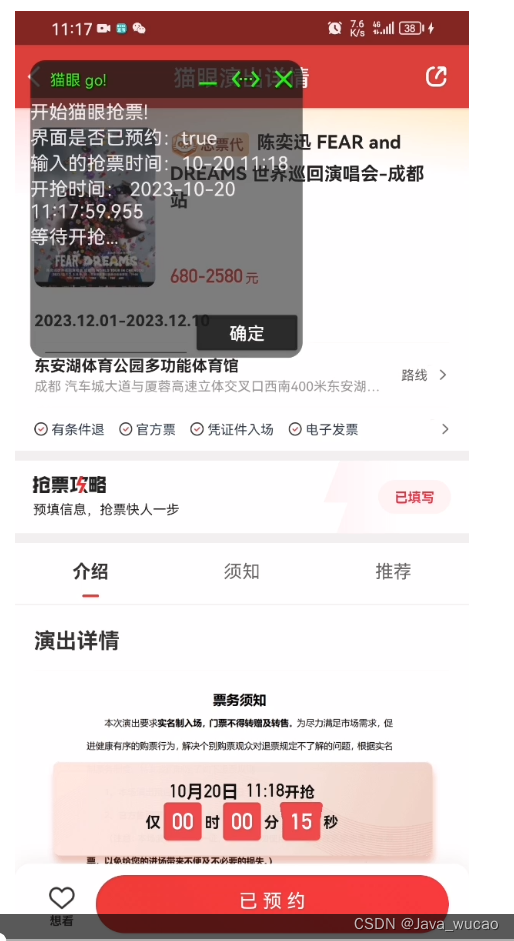
基于自动化工具autox.js的抢票(猫眼)
1.看到朋友圈抢周杰伦、林俊杰演唱会票贼难信息,特研究了一段时间,用autox.js写了自动化抢票脚本,购票页面自动点击下单(仅限安卓手机)。 2.脚本运行图 3.前期准备工作 (1)autox.js社区官网:AutoX.js (2)b站上学习资料:10分钟学会AutoX.js hello world_哔哩哔哩_bi…...

Java架构师内功计算机网络
目录 1 导学2 网络功能和分类3 OSI七层模型3.1 局域网和广域网协议4 TCP/IP协议5 通信技术和交换技术5.1 通信技术5.2 交换技术5.2.1 路由技术5.2.2 传输介质6 通信方式和交换方式7 IP地址7.1 IP地址表示7.2 子网划分8 IPv69 网络规划与设计10 网络存储技术10.1 廉价磁盘几余阵…...

vue 中 mixin 和 mixins 区别
目录 前言 用法 全局Mixin 局部Mixin 代码 理解 高质量的Mixin使用 在Vue.js框架中,Mixin是一种非常重要和强大的功能,它允许开发者创建可复用的代码片段,并将其应用到一个或多个组件中。Vue提供了两种方式来使用Mixin,分别…...
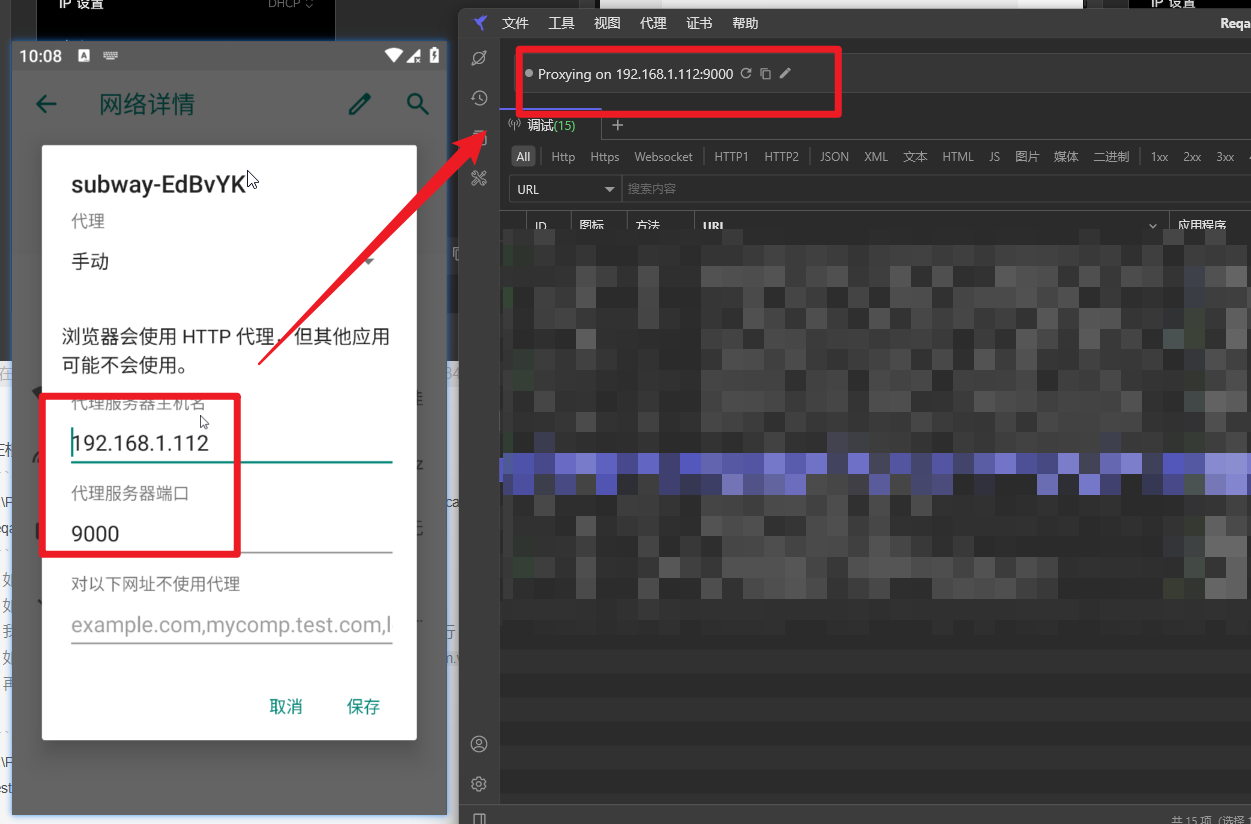
reqable(小黄鸟)+雷电抓包安卓APP
x 下载证书保存到雷电模拟器根目录(安装位置) 为什么? Android7以上,系统允许每个应用可以定义自己的可信CA集,部分的应用默认只会信任系统预装的CA证书,而不会信任用户安装的证书,之前的方法安装Burp/Fiddler证书都是用户证书…...

高等数学啃书汇总重难点(七)微分方程
同济高数上册的最后一章,总的来说,这篇章内容依旧是偏记忆为主,说难不难说简单不简单: 简单的是题型比较死,基本上就是记公式,不会出现不定积分一般花样繁多的情况;然而也就是背公式并不是想的…...

阿里云对象存储OSS文件无法预览,Bucket设置了Referer
您发起的请求头中没有Referer字段或Referer字段为空,与请求Bucket设置的防盗链策略不相符。 解决方案 您可以选择以下任意方案解决该问题。 在请求中增加Referer请求头。 GET /test.txt HTTP/1.1 Date: Tue, 20 Dec 2022 08:48:18 GMT Host: BucketName.oss-examp…...

数字孪生技术:工业数字化转型的引擎
数字孪生是一种将物理实体数字化为虚拟模型的技术,这些虚拟模型与其物理对应物相互关联。这种虚拟模型通常是在数字平台上创建的,它们复制了实际设备、工厂、甚至整个供应链的运作方式。这使工业企业能够实现以下益处: 1. 实时监测和分析 数…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
