机器学习实验三:决策树-隐形眼镜分类(判断视力程度)
决策树-隐形眼镜分类(判断视力程度)
Title : 使用决策树预测隐形眼镜类型
# Description :隐形眼镜数据是非常著名的数据集 ,它包含很多患者眼部状况的观察条件以及医生推荐的隐形眼镜类型 。
# 隐形眼镜类型包括硬材质 、软材质以及不适合佩戴隐形眼镜 。数据来源于UCI数据库
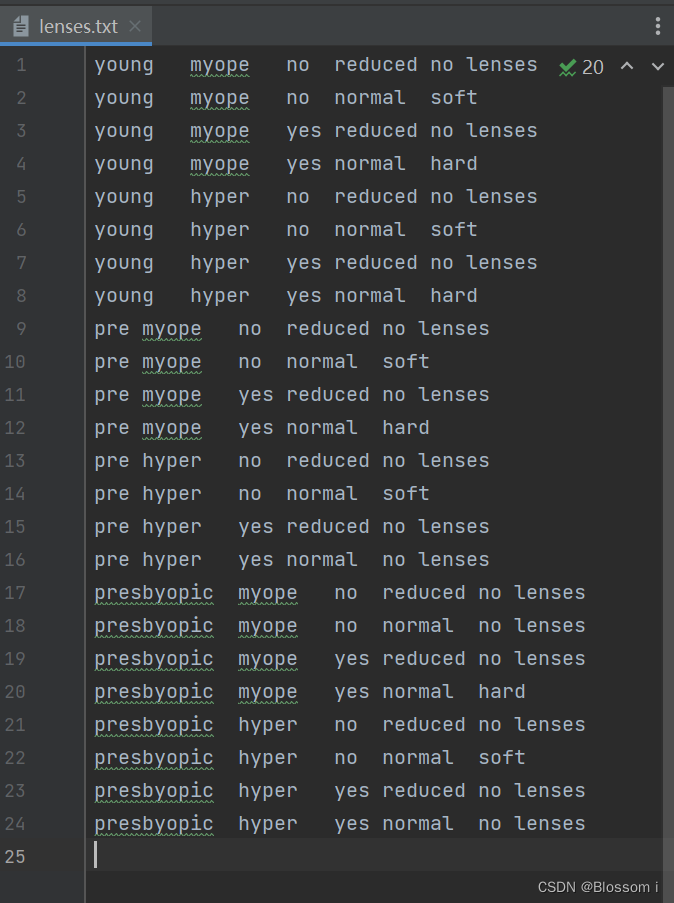
# 为了更容易显示数据,本书对数据做了简单的更改 ,数据存储在源代码下载路径的文本文件中 。
# 本节我们将通过一个例子讲解决策树如何预测患者需要佩戴的隐形眼镜类型。
# 使用小数据集 ,我们就可以利用决策树学到很多知识:眼科医生是如何判断患者需要佩戴的镜片类型;
# 一旦 理解了决策树的工作原理,我们甚至也可以帮助人们判断需要佩戴的镜片类型。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-# Title : 使用决策树预测隐形眼镜类型
# Description :隐形眼镜数据是非常著名的数据集 ,它包含很多患者眼部状况的观察条件以及医生推荐的隐形眼镜类型 。
# 隐形眼镜类型包括硬材质 、软材质以及不适合佩戴隐形眼镜 。数据来源于UCI数据库
# 为了更容易显示数据,本书对数据做了简单的更改 ,数据存储在源代码下载路径的文本文件中 。# 本节我们将通过一个例子讲解决策树如何预测患者需要佩戴的隐形眼镜类型。
# 使用小数据集 ,我们就可以利用决策树学到很多知识:眼科医生是如何判断患者需要佩戴的镜片类型;
# 一旦 理解了决策树的工作原理,我们甚至也可以帮助人们判断需要佩戴的镜片类型。
from math import log
import operator
import matplotlib.pyplot as plt# 计算数据集的香农熵
def calcShannonEnt(dataSet):numEntries = len(dataSet)labelCounts = {}for featVec in dataSet: # 为所有可能分类创建字典currentLabel = featVec[-1] # 取数据集的标签if currentLabel not in labelCounts.keys():labelCounts[currentLabel] = 0 # 分类标签值初始化labelCounts[currentLabel] += 1 # 给标签赋值shannonEnt = 0.0 # 熵初始化for key in labelCounts:prob = float(labelCounts[key])/numEntries # 求得每个标签的概率 # L(Xi) = -log2P(Xi)shannonEnt -= prob * log(prob, 2) # 以2为底求对数 # H = - Σi=1 n P(Xi)*log2P(Xi)# 注意这里是-= 虽然是求和 但是求和值<0 所以这里-=return shannonEnt# 按照给定特征划分数据集
def splitDataSet(dataSet, axis, value):# (待划分的数据集、划分数据集的特征索引、特征的返回值)# 该函数是为了将划分的左右提取出来retDataSet = []for featVec in dataSet:# print("1",featVec)if featVec[axis] == value:# print("2",featVec[axis])reducedFeatVec = featVec[:axis]# print("3",reducedFeatVec)reducedFeatVec.extend(featVec[axis+1:])# print("4",reducedFeatVec)retDataSet.append(reducedFeatVec)# print("5",retDataSet)return retDataSet# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):numFeatures = len(dataSet[0]) - 1 # 计算特征的数目baseEntropy = calcShannonEnt(dataSet) # 计算数据集的原始香农熵 用于与划分完的数据集的香农熵进行比较bestInfoGain = 0.0 # 最佳信息增益初始化bestFeature = -1 # 最佳划分特征初始化 TheBestFeatureToSplitfor i in range(numFeatures): # 遍历所有的特征featList = [example[i] for example in dataSet] # 使用列表推导式创建列表 用于储存每一个数据的第i个特征# [ 表达式 for 变量 in 序列或迭代对象 ] 在这里的执行效果就是 每一列的特征都提取出来# aList = [ x ** 2 for x in range(10) ]# >>>aList [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]uniqueVals = set(featList) # 特征去重newEntropy = 0.0 # 划分后信息熵初始化for value in uniqueVals: # 遍历去重后的特征 分别计算每一个划分后的香农熵subDataSet = splitDataSet(dataSet, i, value) # 划分prob = len(subDataSet)/float(len(dataSet)) # 算概率newEntropy += prob * calcShannonEnt(subDataSet) # 算熵infoGain = baseEntropy - newEntropy # 计算信息增益if (infoGain > bestInfoGain): # 比较划分后的数据集的信息增益是否大于0 大于0 证明划分的有效bestInfoGain = infoGain # 储存最佳信息增益值bestFeature = i # 储存最佳特征值索引return bestFeature # 返回最佳特征值索引"""
函数名称:majorityCnt()
函数说明:统计classList中出现次数最多的元素(类标签)与K-近邻邻近K个元素排序函数功能一致
背景:如果数据集已经处理了所有属性,但是类标签依然不是唯一的
此时我们需要决定如何定义该叶子节点,在这种情况下,我们通常会采用多数表决的方法决定该叶子节点的分类。
Parameters:classList:类标签列表
Returns:sortedClassCount[0][0]:出现次数最多的元素(类标签)
"""
def majorityCnt(classList):classCount = {}for vote in classList:if vote not in classCount.keys():classCount[vote] = 0classCount[vote] += 1sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)return sortedClassCount[0][0]"""函数名称:createTree()函数说明:递归构建决策树 对算法步骤和具体递归赋值操作要多注意parameters:dataSet:数据集 labels:分类属性标签 returns:myTres:决策树
"""
def createTree(dataSet, labels):classList = [example[-1] for example in dataSet]if classList.count(classList[0]) == len(classList): # ["yes","yes"]return classList[0] # 结束划分 如果只有一种分类属性 属性标签重复if len(dataSet[0]) == 1: # 结束划分 如果没有更多的特征了 都为同一类属性标签了return majorityCnt(classList) # 计数排序 取最大数特征bestFeat = chooseBestFeatureToSplit(dataSet) # 获取最优特征索引bestFeatLabel = labels[bestFeat] # 获取最优特征属性标签myTree = {bestFeatLabel: {}} # 决策树初始化 嵌套字典# print("0tree", myTree)del(labels[bestFeat]) # 删除已经使用的特征标签 这时应只剩下有脚蹼特征了featValues = [example[bestFeat] for example in dataSet] # 取出数据集所有最优属性值uniqueVals = set(featValues) # 去重# print("标签%s,标签值%s" % (bestFeatLabel, uniqueVals))# 开始构建决策树for value in uniqueVals:subLabels = labels[:] # 得到剩下的所有特征标签 作为我们的子节点可用# print("1tree", myTree)myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)# 对no surfacing特征 值为1时的赋值是最后一次filppers特征全部分类完毕后# 才将整个filppers的字典值给了关键字1# abc = {"s":{}}# abc["s"][0] = "2"# print(abc) {'s': {0: '2'}}# print("2tree", myTree)return myTree"""函数说明:得到树的叶子结点个数绘制一棵完整的树需要一些技巧。我们虽然有x、y坐标,但是如何放置所有的树节点却是个问题。我们必须知道有多少个叶节点,以便可以正确确定x轴的长度.Parameters:myTree:决策树Return:numLeafs:叶子结点个数
"""
def getNumLeafs(myTree):numLeafs = 0 # 结点数目初始化# firstStr = myTree.keys()[0]# TypeError: 'dict_keys' object does not support indexing# 原因:这是由于python3.6版本改进引起的。# 解决方案:# temp_keys = list(myTree.keys())# firstStr = temp_keys[0]# 在这里 只能取到第一个Key值 其他的key值嵌套在字典里 该方法识别不了 不过正是我们想要的temp_keys = list(myTree.keys()) # mytree: {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}firstStr = temp_keys[0] # 这里我们取到决策树的第一个key值secondDict = myTree[firstStr] # 由于树的嵌套字典格式 我们通过第一个key得到了其value部分的另一个字典for key in secondDict.keys(): # 取出第二字典的key 0和1if type(secondDict[key]).__name__ == 'dict':# 判断是否相应key的value是不是字典 是字典就不是叶子结点# 继续调用本函数拆分该字典直到不是字典 即为叶子结点 进行记录numLeafs += getNumLeafs(secondDict[key])else: # 不是字典直接记录为叶子结点numLeafs += 1return numLeafs"""函数说明:得到树的深度我们还需要确定树的深度,以便于确定y轴的高度Parameters:myTree:决策树Return:maxDepth:树高
"""
def getTreeDepth(myTree):maxDepth = 0# firstStr = myTree.keys()[0]firstStr = next(iter(myTree)) # 这里有第二种方法可以取到到第一个key值secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':# 与记录叶子结点数目类似 一个字典算是一层的代表(因为字典必有分支)thisDepth = 1 + getTreeDepth(secondDict[key])else:# 是叶子结点也给他记作一层 但是要注意 当同一层不单单只是叶子结点 有下层分支时# 会将本来有两层的计数重置为一层 为了避免这一错误 我们有了下面的if判断thisDepth = 1if thisDepth > maxDepth:maxDepth = thisDepthreturn maxDepth"""函数说明:模拟树的创建(自定义的方式)为了避免每次调用都要通过数据集创建树的麻烦Parameters:i:哪个树我们可以多模拟几个数来检测函数的可行性Return:listOfTrees[i]:第i个树
"""
def retrieveTree(i):listOfTrees = [{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}]return listOfTrees[i]decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")"""函数说明:使用文本注解绘制树节点parameters:nodeTxt:注释文段centerPt:文本中心坐标parentPt:箭头尾部坐标nodeType:注释文本类型Return:无返回 执行annotate()画布"""
def plotNode(nodeTxt, centerPt, parentPt, nodeType):createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )"""函数说明:在父子结点间填充文本信息Parameters:cntrPt,parentPt:用于计算标注位置(我们取父子连线的中点作为标注位置)txtString:标注内容Return:None
"""
def plotMidText(cntrPt, parentPt, txtString):xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]# (parentPt[0]+cntrPt[0])/2.0 考虑:# 这次案例中 发现两个公式的树画出来的是相互对称的createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)"""函数说明:绘制决策树---筹备Parameters:myTree:决策树parentPt:父节点位置(在上节中是箭头尾部 箭头头部是子节点)父节点----->子节点nodeTxt:标注信息Special:numLeafs:当前结点的叶子节点数(是在变的)tatalW:树的总叶子数Return:None
"""
def plotTree(myTree, parentPt, nodeTxt):numLeafs = getNumLeafs(myTree) # 得到叶子结点计算树的宽度depth = getTreeDepth(myTree) # 得到树深度firstStr = list(myTree.keys())[0] # 得到根结点(父节点)注释内容cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)# 根节点位置# 第一次看非常之疑惑 plotTree.xOff、plotTree.totalW、plotTree.yOff 三个突兀的东西就这样出现了# 一开始以为是定义函数对象的调用 又想了想不太对劲 自己调用自己啥的也没有对三变量定义的过程啊 还是重复这样# 搜了很多没发现什么雷同的 看书上解释是一种全局变量 但还是不理解 毕竟是第一次见# 换了个方向搜索 仍然无果而终 最后用type()检测变量 的确是个变量 好吧 难受的心路历程# 由于按顺序去看的函数没有先看下面的执行函数 发现 执行函数中确实有提前定义这几个变量 全局变量石锤# 现在唯一的疑惑就是 为什么可以这样定义?有什么意义?# 猜测:由于执行函数会调用多个函数来实现总的绘图 所以我们需要用函数名.变量 这样的形式来区分应用于哪个函数# 当然这种变量也可以放在需求函数里面定义 但是由于此处变量需要inTree变量来计算值所以就干脆放在执行函数里面了# 执行函数的参数恰好就是inTree (图个方便?)# 巧妙的分析一波 哈哈啊哈哈plotMidText(cntrPt, parentPt, nodeTxt) # 画连线标注plotNode(firstStr, cntrPt, parentPt, decisionNode) # 画结点 画线secondDict = myTree[firstStr] # 解析下一个字典(根节点)/叶子plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD # 计算下一个结点的yfor key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict': # 子树plotTree(secondDict[key], cntrPt, str(key))else: # 叶子节点plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalWplotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD# 递归完后需要回退到上层,绘制当前树根节点的其他分支节点。"""函数说明:绘制决策树---执行Parameters:inTree:决策树Return:None 展示画布
"""
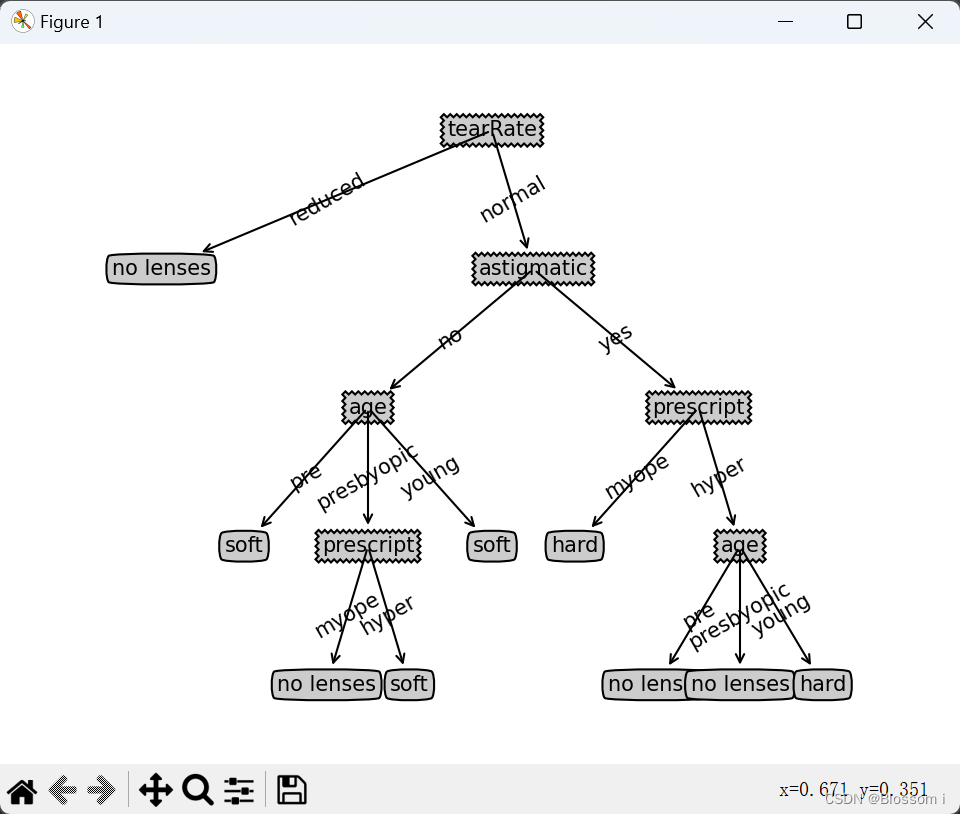
def createPlot(inTree):fig = plt.figure(1, facecolor='white')fig.clf()axprops = dict(xticks=[], yticks=[]) # 定义x,y轴为空 为后面不显示轴作准备createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # 传入刚才定义参数 构造子图# createPlot.ax1 = plt.subplot(111, frameon=False) # 有轴的plotTree.totalW = float(getNumLeafs(inTree))# tatalW:树的宽度初始化 = 叶子节点plotTree.totalD = float(getTreeDepth(inTree))# tatalD:树的深度 = 树高plotTree.xOff = -0.5/plotTree.totalW # 为开始x位置为第一个表格左边的半个表格距离位置plotTree.yOff = 1.0 # y位置1# 使用两个全局变量plotTree.xOff、plotTree.yOff追踪已经绘制的节点位置# 这部分代码直接去看很难理解 之后会有注解plotTree(inTree, (0.5, 1.0), '') # 调用函数开始绘图 一开始标注为空 因为第一个就是根结点plt.show()def prodict():# str通过encode()方法可以编码为指定的bytes;# 反过来,如果我们从网络或磁盘上读取了字节流,那么读到的数据就是bytes。要把bytes变为str,就需要用decode()方法# 这里读文件读到的是字节 需要转化为strwith open("lenses.txt", "rb") as fr: # 取出数据集lenses = [inst.decode().strip().split('\t')for inst in fr.readlines()]# 解析由tap键分割的数据 去除数据左右的空格# 这里强调一下 决策树的数据集是由 特征属性值和分类标签两部分组成的lensesLabels = ['age', 'prescript', 'astigmatic', "tearRate"] # 设置特征属性lensesTree = createTree(lenses, lensesLabels) # 创造样本决策树(分类器)createPlot(lensesTree)return lensesTree# , lensesLabels"""
函数说明:对决策树进行分类
Parameters:inputTree:决策树featLabels:数据集中label顺序列表testVec:两个特征的属性值[特征一,特征二]
Rertun:classLabel:预测结果根据两个特征的属性值来预测分类
"""
def classify(inputTree, featLabels, testVec):firstStr = list(inputTree.keys())[0] # 得到首key值secondDict = inputTree[firstStr] # 首key的value--->下一个分支featIndex = featLabels.index(firstStr) # 确定根节点是标签向量中的哪一个(索引)key = testVec[featIndex] # 确定一个条件后的类别或进入下一个分支有待继续判别# 这里要注意 我们并不知道目前的这个结点(也就是特征)在数据集中的具体位置 [0,1,no]# 是第一个 还是第二个 所以需要用具体值再找索引的方式# 找到了索引之后 我们就可以确定他是数据集中的哪一个值# (这里再强调一下 数据集中特征的属性值的顺序 与 标签向量label中特征的顺序是一致的)# dataSet = [[1, 1, 'yes']]# labels = ['no surfacing', 'flippers']# 这样一来计算机就知道了该在你放入的测试数据集寻找哪一个作为当前节点的预测值了# 我们又用该索引去查找测试列表处该结点给的预测值是0还是1# 是0相当于找了no预测值 是1 证明还需要判断或者是yes预测值valueOfFeat = secondDict[key]if isinstance(valueOfFeat, dict): # 判断实例函数 和 type函数类似 但是这个更好一点classLabel = classify(valueOfFeat, featLabels, testVec)else:classLabel = valueOfFeatreturn classLabelif __name__ == "__main__":# mytree, labels = prodict() 这里返回的标签不完整 因为之前调用createTree()时 取最优特征后删除了它在列表中的存在# 另外 只要一个返回值就删除另一个 不然只接受一个返回值# 计算机会将返回值变成元组类型 会在其他函数中需求取到列表的key值的时候 产生不必要的麻烦mytree = prodict()labels = ['age', 'prescript', 'astigmatic', "tearRate"]result = classify(mytree, labels, ["presbyopic", "hyper", "yes", "normal"])if result == 'no lenses':print("实力良好")if result == 'soft':print("轻微近视")if result == 'hard':print("重度近视")# >>>视力良好
运行大概15分钟左右
相关文章:

机器学习实验三:决策树-隐形眼镜分类(判断视力程度)
决策树-隐形眼镜分类(判断视力程度) Title : 使用决策树预测隐形眼镜类型 # Description :隐形眼镜数据是非常著名的数据集 ,它包含很多患者眼部状况的观察条件以及医生推荐的隐形眼镜类型 。 # 隐形眼镜类型包括硬材质 、软材质以及不适合佩…...

广州华锐互动:VR技术应用到工程项目施工安全培训的好处
随着科技的飞速发展,虚拟现实(VR)技术已经深入到各个领域。在建筑施工领域,VR技术的应用为工程项目施工安全培训带来了许多好处。本文将探讨VR技术在这方面的优势和应用。 首先,VR技术能够提供沉浸式的安全培训体验。通过VR设备,学…...

Hadoop3.0大数据处理学习1(Haddop介绍、部署、Hive部署)
Hadoop3.0快速入门 学习步骤: 三大组件的基本理论和实际操作Hadoop3的使用,实际开发流程结合具体问题,提供排查思路 开发技术栈: Linux基础操作、Sehll脚本基础JavaSE、Idea操作MySQL Hadoop简介 Hadoop是一个适合海量数据存…...
C笔记:引用调用,通过指针传递
代码 #include<stdio.h> int max1(int num1,int num2) {if(num1 < num2){num1 num2;}else{num2 num1;} } int max2(int *num1,int *num2) {if(num1 < num2){*num1 *num2; // 把 num2 赋值给 num1 }else{*num2 *num1;} } int main() {int num1 0,num2 -2;int…...
【方法】如何给PDF文件添加“打开密码”?
PDF文件可以在线浏览,但如果想要给文件添加“打开密码”,就需要用到软件工具,下面小编分享两种常用的工具,小伙伴们可以根据需要选择。 工具一:PDF编辑器 PDF阅读器一般是没有设置密码的功能模块,PDF编辑器…...
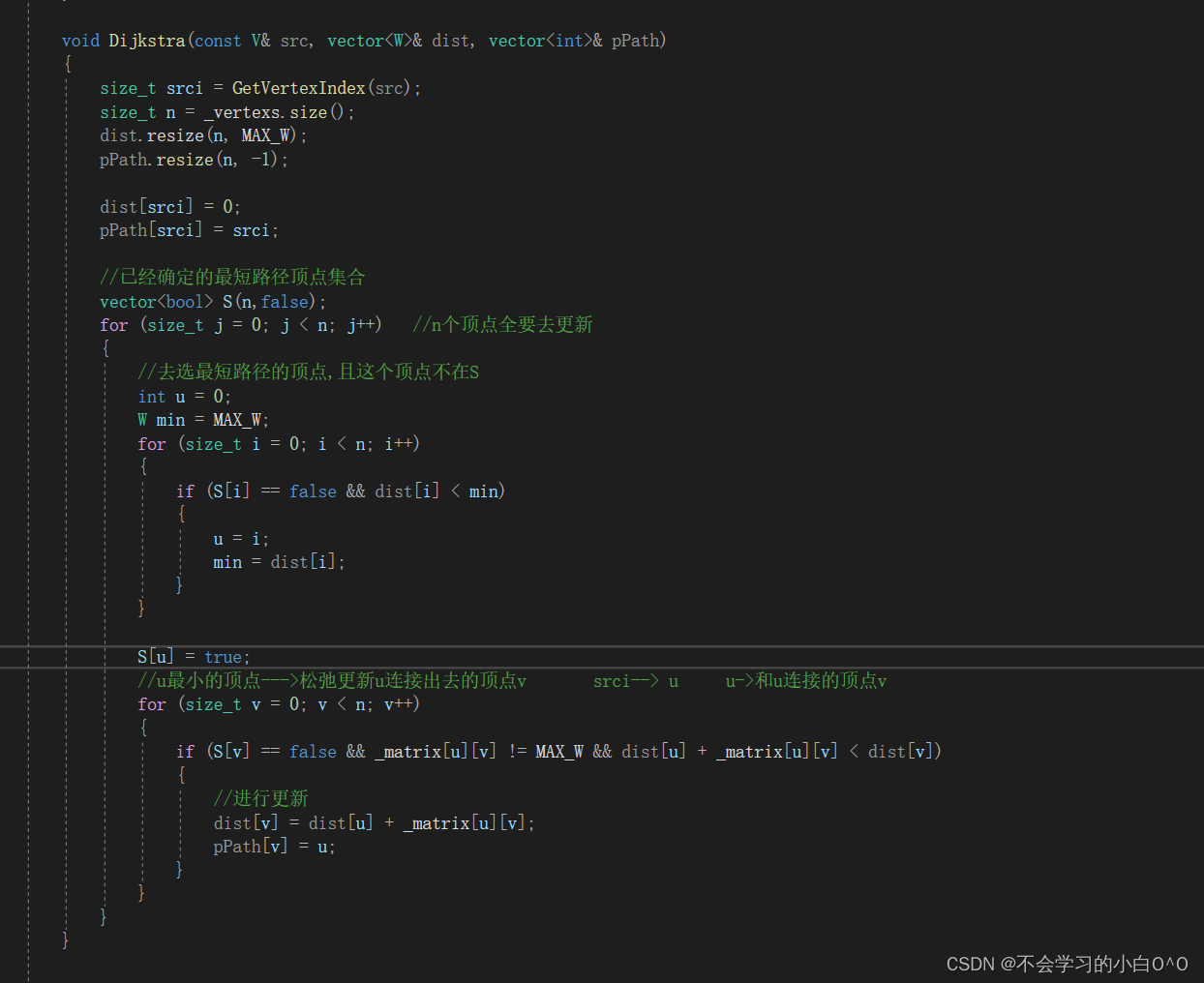
单源最短路径 -- Dijkstra
Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题 -- 同时算法要求图中所有边的权重非负(这个很重要) 针对一个带权有向图G , 将所有节点分为两组S和Q , S是已经确定的最短路径的节点集合,在初始时为空&…...

Java--多态及抽象类与接口
1.多态 以不同参数调用父类方法,可以得到不同的处理,子类中无需定义相同功能的方法,避免了重复代码编写,只需要实例化一个继承父类的子类对象,即可调用相应的方法,而只需要维护附父类方法即可。 package c…...
Python手搓C4.5决策树+Azure Adult数据集分析
前言 课上的实验 由于不想被抄袭,所以暂时不放完整代码 Adult数据集可以在Azure官网上找到 Azure 开放数据集中的数据集 - Azure Open Datasets | Microsoft Learn 数据集预处理 删除难以处理的权重属性fnlwgt与意义重复属性educationNum去除重复行与空行删除…...

【tg】6: MediaManager的主要功能
【tg】2:视频采集的输入和输出 的管理者是 media manager‘ media 需要 network的支持:NetworkInterface friend class MediaManager::NetworkInterfaceImpl;NetworkInterfaceImpl 直接持有 MediaManager 的指针即可:发送rtp包、rtcp包、设置socket选项?...

NPM-安装报错connect ETIMEDOUT
报错信息request to https://registry.npm.taobao.org/yarn failed, reason: connect ETIMEDOUT 解决方案: 1、npm set strict-ssl false 2、设置代理 npm config set proxy http://xxx:xxxopenproxy.ali.com:8080npm如何在安装的时候指定源 npm install -g yarn1.…...

机器学习之查准率、查全率与F1
文章目录 查准率(Precision):查全率(Recall):F1分数(F1 Score):实例P-R曲线F1度量python实现 查准率(Precision): 定义: …...
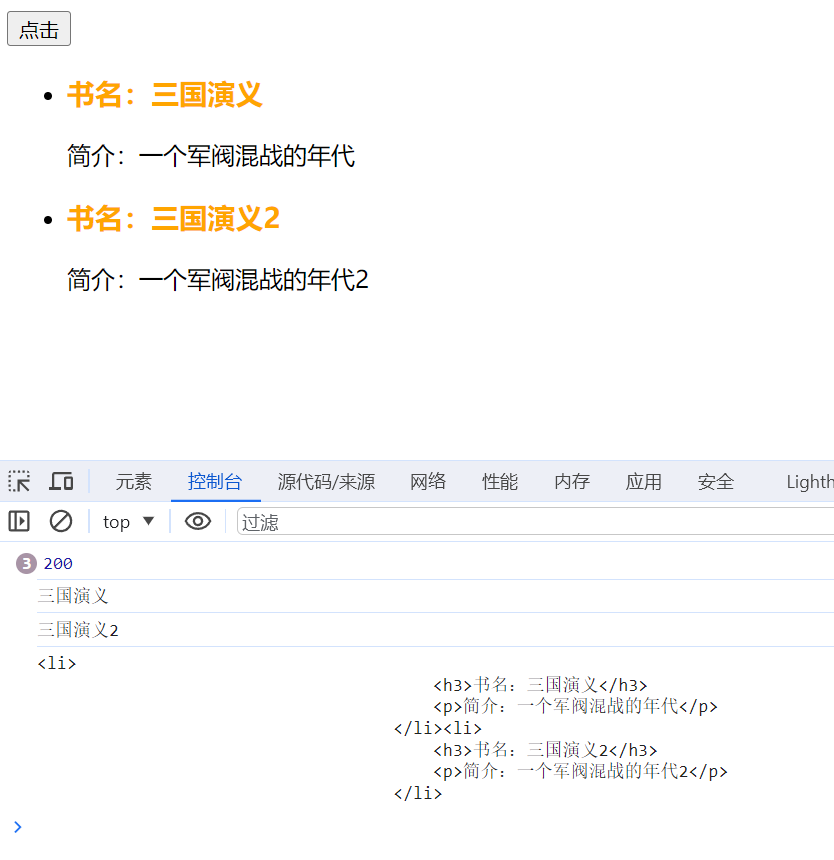
*Django中的Ajax 纯js的书写样式1
搭建项目 建立一个Djano项目,建立一个app,建立路径,视图函数大多为render, Ajax的创建 urls.py path(index/,views.index), path(index2/,views.index2), views.py def index(request):return render(request,01.html) def index2(requ…...

谈谈node架构中的线程进程的应用场景、事件循环及任务队列
本文作者系360奇舞团前端开发工程师 文章标题:谈谈node架构中的线程进程的应用场景、事件循环及任务队列 Node.js是一个基于Chrome V8引擎的JavaScript运行时环境,nodejs是单线程执行的,它基于事件驱动和非阻塞I/O模型进行多任务的执行。在理…...

http代理IP它有哪些应用场景?如何提升访问速度?
随着互联网的快速发展,越来越多的人开始关注网络速度和安全性。其中,代理IP技术作为一种有效的网络加速和安全解决方案,越来越受到人们的关注。那么,http代理IP有哪些应用场景?又如何提升访问速度呢? 一、h…...

Armv8/Armv9的VIPT的别名问题是如何解决的
https://www.cse.unsw.edu.au/~cs9242/02/lectures/03-cache/node8.html https://developer.arm.com/documentation/ddi0406/b/System-Level-Architecture/Virtual-Memory-System-Architecture–VMSA-/Address-mapping-restrictions...
java/javaswing/窗体程序,人脸识别系统,人脸追踪,计算机视觉
源码下载地址 支持:远程部署/安装/调试、讲解、二次开发/修改/定制 源码下载地址...
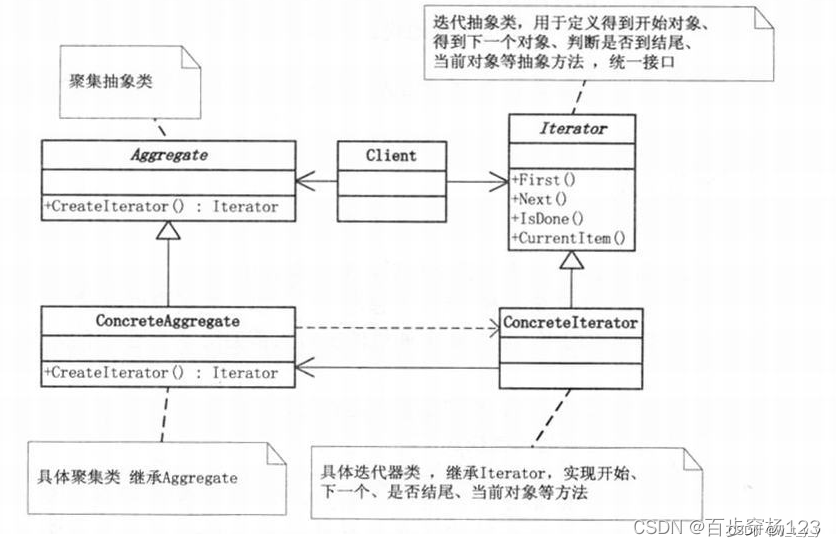
设计模式(16)迭代器模式
一、介绍: 1、定义:迭代器模式 (Iterator Pattern) 是一种行为型设计模式,它提供一种顺序访问聚合对象(如列表、集合等)中的元素,而无需暴露聚合对象的内部表示。迭代器模式将遍历逻辑封装在一个迭代器对象…...
Openssl数据安全传输平台011:秘钥协商服务端
0. 代码仓库 https://github.com/Chufeng-Jiang/OpenSSL_Secure_Data_Transmission_Platform/tree/main/Preparation 编译protobuf类文件 VS2022 protobuf3.17 Message.proto protoc Message.proto --cpp_out./...

【23种设计模式】里氏替换原则
个人主页:金鳞踏雨 个人简介:大家好,我是金鳞,一个初出茅庐的Java小白 目前状况:22届普通本科毕业生,几经波折了,现在任职于一家国内大型知名日化公司,从事Java开发工作 我的博客&am…...

嵌入式系统设计师考试笔记之操作系统基础复习笔记一
目录 1、嵌入式软件基础 (1)嵌入式软件的特点: (2)嵌入式软件分类: (3)无操作系统的嵌入式软件的两种实现方式: (4)有操作系统的三大优点&am…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
