67 跳跃游戏 II
跳跃游戏 II
- 题解1 贪心1 正向
- 题解2 贪心2 反向
- 题解3 DP
给定一个长度为
n 的
0 索引整数数组
nums。初始位置为
nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达nums[n - 1]的最小跳跃次数。生成的测试用例可以到达nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
- 1 <=
nums.length<= 1 0 4 10^4 104 - 0 <=
nums[i]<= 1000
题目保证可以到达nums[n-1]
题解1 贪心1 正向
class Solution {
public:int jump(vector<int>& nums) {const int s = nums.size();if(1 == s) return 0;// 用 i 和 tmpend 标记了可以选择的跳跃步数// maxrl标记了所有选择 [i..end] 中能够跳到的最远距离// step 记录跳跃次数。int maxrl = 0;int step = 0;int tmpend = 0;// 不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了for(int i = 0; i < s-1; i++){maxrl = max(maxrl, i+nums[i]);if(i == tmpend){step ++;tmpend = maxrl;// 如果不限制i是否到最后一个位置即 i < s 加上这段/**if(tmpend >= s-1)return step;**/}}return step;}
};

题解2 贪心2 反向
如果有多个位置通过跳跃都能够到达最后一个位置,那么我们应该如何进行选择呢?
直观上来看,我们可以「贪心」地选择距离最后一个位置最远的那个位置,也就是对应下标最小的那个位置。
因此,我们可以从左到右遍历数组,选择第一个满足要求的位置。
class Solution {
public:int jump(vector<int>& nums) {const int s = nums.size();int step = 0;int pos = s-1;while(pos > 0){// i<pos :考虑最后一步跳跃前所在的位置,该位置通过跳跃能够到达最后一个位置for(int i = 0; i < pos; i++){if(i + nums[i] >= pos){pos = i;step ++;break; // 回到while}}}return step;}
};

题解3 DP
class Solution {
public:int jump(vector<int>& nums) {const int s = nums.size();vector<int> dp(s, INT_MAX-1);// 初始化dp[0] = 0;for(int i = 1; i < s; i++){for(int j = 0; j < i; j++){if(nums[j] >= i-j)dp[i] = min(dp[i], dp[j]+1);}}return dp[s-1];}
};

相关文章:

67 跳跃游戏 II
跳跃游戏 II 题解1 贪心1 正向题解2 贪心2 反向题解3 DP 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 &…...
rust解法)
客户中心模拟(Queue and A, ACM/ICPC World Finals 2000, UVa822)rust解法
你的任务是模拟一个客户中心运作情况。客服请求一共有n(1≤n≤20)种主题,每种主题用5个整数描述:tid, num, t0, t, dt,其中tid为主题的唯一标识符,num为该主题的请求个数,t0为第一个请求的时刻&…...

方案聚焦:高可用的F5分布式云DNS负载均衡
DNS是实现互联网的主要技术之一。它也是网络基础设施的重要组成部分,DNS管理一个分布式和冗余的架构,确保高可用性和高质量的用户响应时间,因此拥有一个可用的、智能的、安全和可扩展的DNS基础设施是至关重要的。然而DNS没有真正的能力来分配…...

大数据性能测试方案-V1.0
XXX大数据平台 性能测试方案 [V1-1.0] 拟 制 人: 审 核 人: 批 准 人: [xxxx年xx月xx日]...

Kafak - 单机/集群快速安装指北(3.x版本)
文章目录 官方下载地址上传安装包解压安装包到指定目录修改解压包名为kafka修改config目录下的配置文件server.propertie配置环境变量其他机器同上 - 修改配置文件中的brokerid启动集群停止Kraft 方式部署集群----(不使用zookeeper) 官方下载地址 http://kafka.apache.org/dow…...

互联网Java工程师面试题·Spring篇·第五弹
目录 1、什么是 spring? 2、使用 Spring 框架的好处是什么? 3、Spring 由哪些模块组成? 4、核心容器(应用上下文) 模块。 5、BeanFactory – BeanFactory 实现举例。 6、XMLBeanFactory 7、解释 AOP 模块 8、解释 JDBC 抽象和 DAO 模块。 9、…...

XTU-OJ 1221-Binary
题目描述 给你一个非负整数n(0≤n≤232-1),求其二进制里面最长连续1数码的长度。 比如,7的二进制为111,所以最长连续1数码的长度为3;13的二进制为1101,所以最长连续1数码的长度为2. 输入 第一行是一个整数K(K≤20000),表示样例的个…...
)
Chromium源码由浅入深(三)
接前一篇文章:Chromium源码由浅入深(二) 上一回说到了关键的“钥匙”:browserBridge.gpuInfo,本文就针对其进行深入探究。 先来看前半部分,browserBridge。 在content/browser/resources/gpu/gpu_interna…...
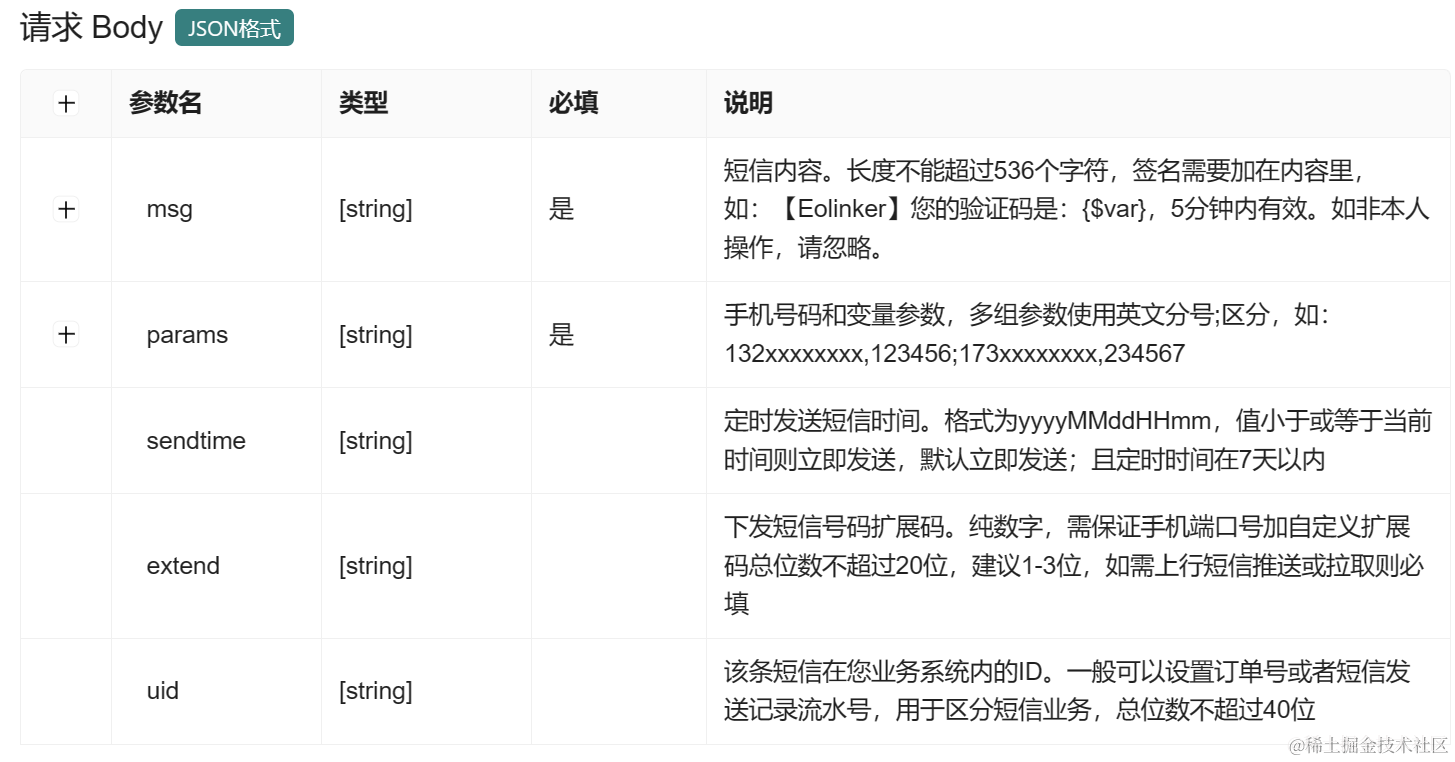
如何集成验证码短信API到你的应用程序
引言 当你需要为你的应用程序增加安全性和用户验证功能时,集成验证码短信API是一个明智的选择。验证码短信API可以帮助你轻松实现用户验证、密码重置和账户恢复等功能,提高用户体验并增强应用程序的安全性。本文将介绍如何将验证码短信API集成到你的应用…...
)
Linux- 由映射文件I/O问题引出的SIGBUS 空洞文件(Sparse File)
SIGBUS SIGBUS是一个在Unix-like操作系统中的信号,它通常表示非法访问内存,而这种非法访问的原因与常见的SIGSEGV(段错误)有所不同。以下是可能导致SIGBUS的常见情况: 未对齐的内存访问:某些硬件平台要求数…...

代码随想录图论 第二天 | 695. 岛屿的最大面积 1020. 飞地的数量
代码随想录图论 第二天 | 695. 岛屿的最大面积 1020. 飞地的数量 一、695. 岛屿的最大面积 题目链接:https://leetcode.cn/problems/max-area-of-island/ 思路:典型的遍历模板题,我采用深度优先,每块岛屿递归遍历的时候计数&…...

R语言代码示例
以下是一个使用R语言和httrOAuth库的下载器程序,用于下载的内容。程序使用以下代码。 # 安装和加载必要的库 install.packages("httr") install.packages("httrOAuth") library(httr) library(httrOAuth) # 设置 http_proxy <- "du…...

ESP32网络开发实例-将 ESP32 连接到 EMQX Cloud MQTT Broker
将 ESP32 连接到 EMQX Cloud MQTT Broker 文章目录 将 ESP32 连接到 EMQX Cloud MQTT Broker1、MQTT介绍2、软件准备3、硬件准备4、代码实现5、MQTT测试在本文中,将介绍使用 EMQX Cloud MQTT 服务器。 首先,我们将介绍如何将 ESP32 开发板连接到 EMQX Cloud MQTT 服务器。 我…...
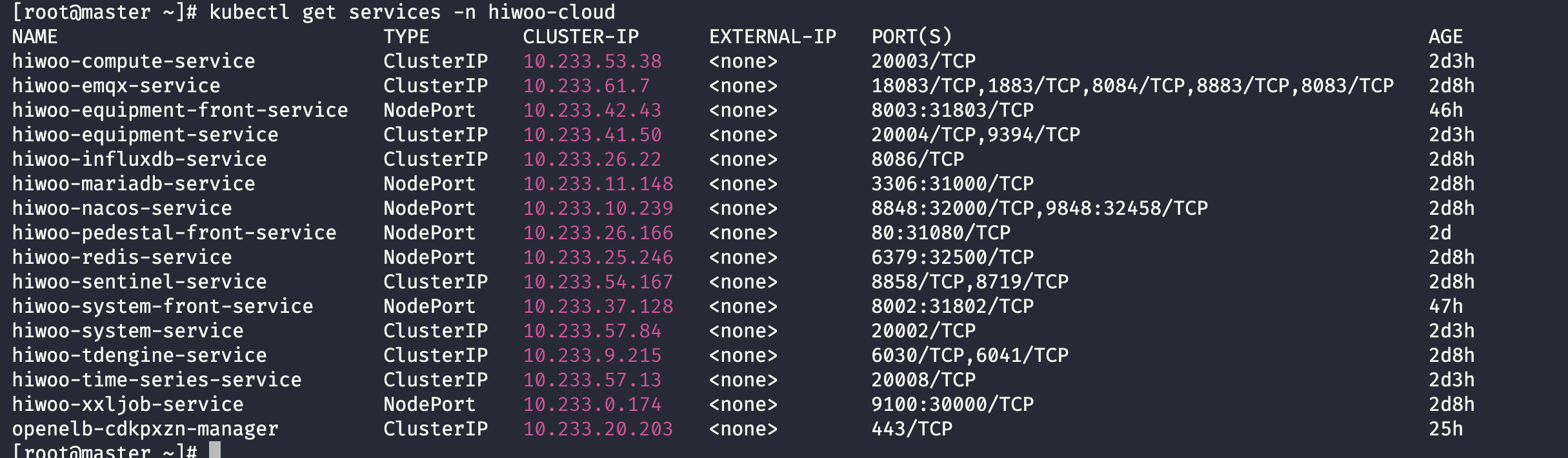
基于Kubesphere容器云平台物联网云平台Devops实践
基于Kubesphere容器云平台物联网云平台Devops实践 项目背景 公司是做工业物联网相关业务的,现业务是云平台,技术栈 后端为 Springboot2.7JDK11 ,前端为 Vue3Ts,需要搭建自动化运维平台以实现业务代码自动部署上线,…...
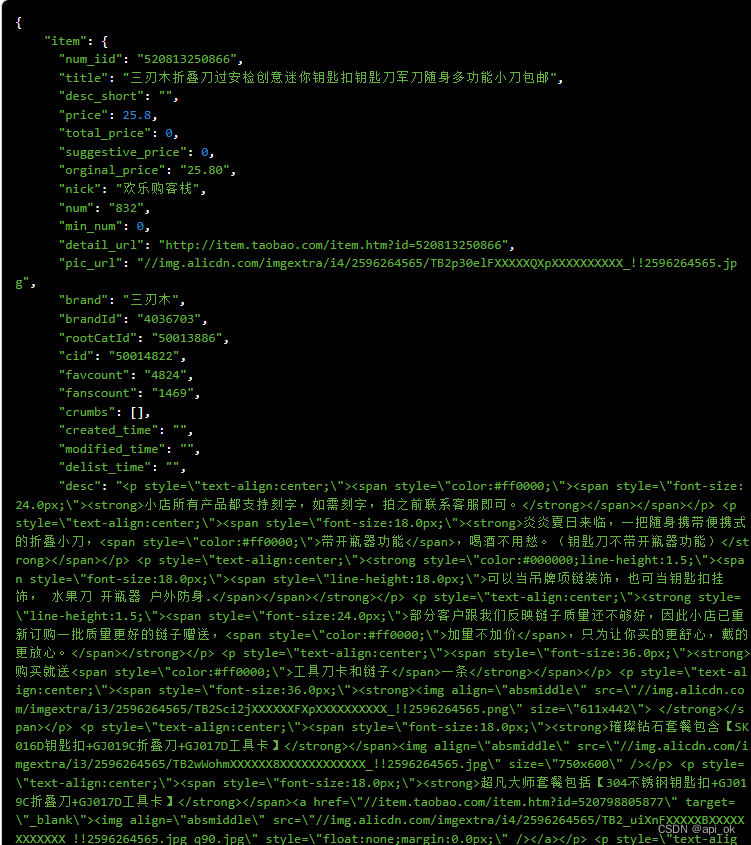
淘宝商品详情页API接口|tb获取商品主图接口
淘宝的 API 开发接口,我们需要做下面几件事情。 1)开放平台注册开发者账号; 2)然后为每个淘宝应用注册一个应用程序键(App Key) ; 3)下载淘宝 API 的 SDK 并掌握基本的 API 基础知识和调用&a…...
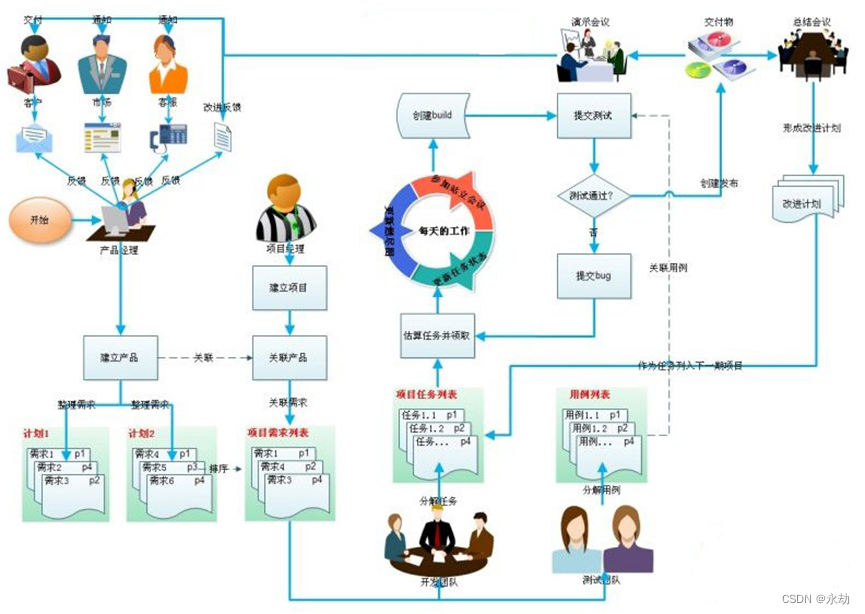
JAVA面试笔记
JAVA就业课程 面试整体流程 1.1 简单的自我介绍 我是xxxx,工作xxx年.我先后在xxxx公司、yyyy公司工作。先后做个xxxx项目、yyyy项目。 1.2 你简单介绍一下xxxx项目 为了解决xxxx问题,开发了一套xxxx系统,该系统主要有那些部分组成。简单介绍项目的整体架…...

尚硅谷Flume(仅有基础)
q 1 概述 1.1 定义 Flume 是Cloudera 提供的一个高可用的,高可靠的,分布式的海量日志采集、聚合和传输的系统。Flume 基于流式架构,灵活简单。 Flume最主要的作用就是,实时读取服务器本地磁盘的数据,将数据写入到HD…...

JS中this的绑定规则
如果有人问你this指向哪里?但又不给你说调用位置,那他就是在耍流氓。 – 龚港浩 1、默认绑定 首先要介绍的是最常用的函数调用类型:独立函数调用。可以把这条规则看作是无法应用其他规则时的默认规则。 function foo() {console.log( this…...
酷开科技 | 酷开系统大屏电视,打造精彩家庭场景
在信息资讯不发达的年代,电视机一直都是个人及家庭重要的信息获取渠道和家庭娱乐中心,是每个家庭必不可少的大家电之一!在快节奏的现代生活中,受手机和平板的冲击,电视机这个曾经的客厅“霸主”一度失去了“主角光环”…...

GDPU 数据结构 天码行空6
一、实验目的 1、掌握串的顺序存储结构 2、掌握顺序串的基本操作方法(插入、删除等)。 3、掌握串的链式存储结构。 4、掌握链式串的几种基本操作(插入、删除等)。 5、掌握Brute-Force算法 二、实验内容 1、编写函数BFIndex(Str…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
