synchronized 、ReentrantLock
synchronized 和 ReentrantLock 都是用于实现多线程同步的机制:
-
锁的获取方式:
synchronized是内置的 Java 关键字,它通过对象的内置监视器来获取锁。每个对象都有一个关联的监视器,只有一个线程可以获得对象的监视器,其他线程必须等待。ReentrantLock是一个类,它提供了显式的锁,通过创建ReentrantLock实例并调用其lock()方法来获取锁。
-
可中断性:
ReentrantLock支持可中断的锁获取,即线程可以在等待锁的过程中响应中断。synchronized不支持可中断性,一旦线程等待锁,只能等待锁被释放或线程被中断。
-
公平性:
ReentrantLock可以选择是否使用公平锁。公平锁会按照请求锁的顺序分配锁,确保所有线程都有机会获得锁。非公平锁则不考虑等待线程的顺序。synchronized是非公平锁,不考虑等待线程的顺序。
-
灵活性:
ReentrantLock提供了更多的灵活性,如超时获取锁、尝试获取锁、条件等待等功能。这使得它在某些复杂的同步需求下更有优势。synchronized提供的功能相对较少。 </
相关文章:

synchronized 、ReentrantLock
synchronized 和 ReentrantLock 都是用于实现多线程同步的机制: 锁的获取方式: synchronized 是内置的 Java 关键字,它通过对象的内置监视器来获取锁。每个对象都有一个关联的监视器,只有一个线程可以获得对象的监视器,其他线程必须等待。ReentrantLock 是一个类,它提供了…...
用VSCODE启动Java项目
下载插件 推荐下载插件 启动 在vscode中打开项目或将项目拖进vscode,等进度条加载完成即成启动项目...

最简单的修改linux系统上Docker的镜像源
前言 是不是从docker上下载镜像总是很慢 我有两个物理服务器,两个都在本地不能访问国际网络,那只能使用国内网络,就是下载docker镜像太慢了,慢的我心情都不好了,所以就出了这篇文章用来解决docker下载慢的问题 正文 1.首先你得下载好docker,在Linux上,下载Docker的命令是下面这…...

layui移除(删除)table表格的一行
表格里添加删除按钮: , {field: wealth, width: 150, title: 操作, align: center, fixed: right,templet: function (item) {return <a style"margin:0px 5px; color:red; cursor: pointer;" lay-event"delete" id"DeleteTr" >…...

67 跳跃游戏 II
跳跃游戏 II 题解1 贪心1 正向题解2 贪心2 反向题解3 DP 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 &…...
rust解法)
客户中心模拟(Queue and A, ACM/ICPC World Finals 2000, UVa822)rust解法
你的任务是模拟一个客户中心运作情况。客服请求一共有n(1≤n≤20)种主题,每种主题用5个整数描述:tid, num, t0, t, dt,其中tid为主题的唯一标识符,num为该主题的请求个数,t0为第一个请求的时刻&…...

方案聚焦:高可用的F5分布式云DNS负载均衡
DNS是实现互联网的主要技术之一。它也是网络基础设施的重要组成部分,DNS管理一个分布式和冗余的架构,确保高可用性和高质量的用户响应时间,因此拥有一个可用的、智能的、安全和可扩展的DNS基础设施是至关重要的。然而DNS没有真正的能力来分配…...

大数据性能测试方案-V1.0
XXX大数据平台 性能测试方案 [V1-1.0] 拟 制 人: 审 核 人: 批 准 人: [xxxx年xx月xx日]...

Kafak - 单机/集群快速安装指北(3.x版本)
文章目录 官方下载地址上传安装包解压安装包到指定目录修改解压包名为kafka修改config目录下的配置文件server.propertie配置环境变量其他机器同上 - 修改配置文件中的brokerid启动集群停止Kraft 方式部署集群----(不使用zookeeper) 官方下载地址 http://kafka.apache.org/dow…...

互联网Java工程师面试题·Spring篇·第五弹
目录 1、什么是 spring? 2、使用 Spring 框架的好处是什么? 3、Spring 由哪些模块组成? 4、核心容器(应用上下文) 模块。 5、BeanFactory – BeanFactory 实现举例。 6、XMLBeanFactory 7、解释 AOP 模块 8、解释 JDBC 抽象和 DAO 模块。 9、…...

XTU-OJ 1221-Binary
题目描述 给你一个非负整数n(0≤n≤232-1),求其二进制里面最长连续1数码的长度。 比如,7的二进制为111,所以最长连续1数码的长度为3;13的二进制为1101,所以最长连续1数码的长度为2. 输入 第一行是一个整数K(K≤20000),表示样例的个…...
)
Chromium源码由浅入深(三)
接前一篇文章:Chromium源码由浅入深(二) 上一回说到了关键的“钥匙”:browserBridge.gpuInfo,本文就针对其进行深入探究。 先来看前半部分,browserBridge。 在content/browser/resources/gpu/gpu_interna…...
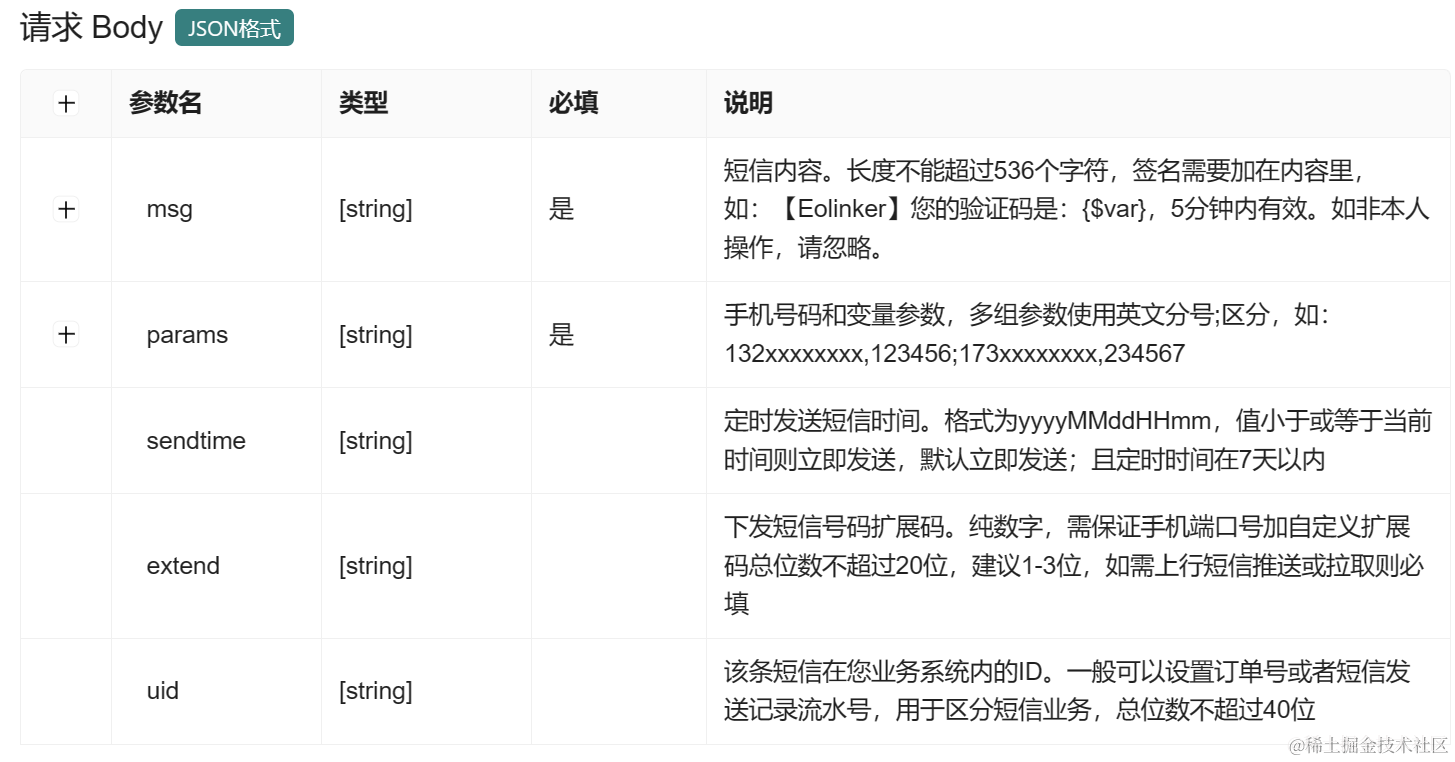
如何集成验证码短信API到你的应用程序
引言 当你需要为你的应用程序增加安全性和用户验证功能时,集成验证码短信API是一个明智的选择。验证码短信API可以帮助你轻松实现用户验证、密码重置和账户恢复等功能,提高用户体验并增强应用程序的安全性。本文将介绍如何将验证码短信API集成到你的应用…...
)
Linux- 由映射文件I/O问题引出的SIGBUS 空洞文件(Sparse File)
SIGBUS SIGBUS是一个在Unix-like操作系统中的信号,它通常表示非法访问内存,而这种非法访问的原因与常见的SIGSEGV(段错误)有所不同。以下是可能导致SIGBUS的常见情况: 未对齐的内存访问:某些硬件平台要求数…...

代码随想录图论 第二天 | 695. 岛屿的最大面积 1020. 飞地的数量
代码随想录图论 第二天 | 695. 岛屿的最大面积 1020. 飞地的数量 一、695. 岛屿的最大面积 题目链接:https://leetcode.cn/problems/max-area-of-island/ 思路:典型的遍历模板题,我采用深度优先,每块岛屿递归遍历的时候计数&…...

R语言代码示例
以下是一个使用R语言和httrOAuth库的下载器程序,用于下载的内容。程序使用以下代码。 # 安装和加载必要的库 install.packages("httr") install.packages("httrOAuth") library(httr) library(httrOAuth) # 设置 http_proxy <- "du…...

ESP32网络开发实例-将 ESP32 连接到 EMQX Cloud MQTT Broker
将 ESP32 连接到 EMQX Cloud MQTT Broker 文章目录 将 ESP32 连接到 EMQX Cloud MQTT Broker1、MQTT介绍2、软件准备3、硬件准备4、代码实现5、MQTT测试在本文中,将介绍使用 EMQX Cloud MQTT 服务器。 首先,我们将介绍如何将 ESP32 开发板连接到 EMQX Cloud MQTT 服务器。 我…...
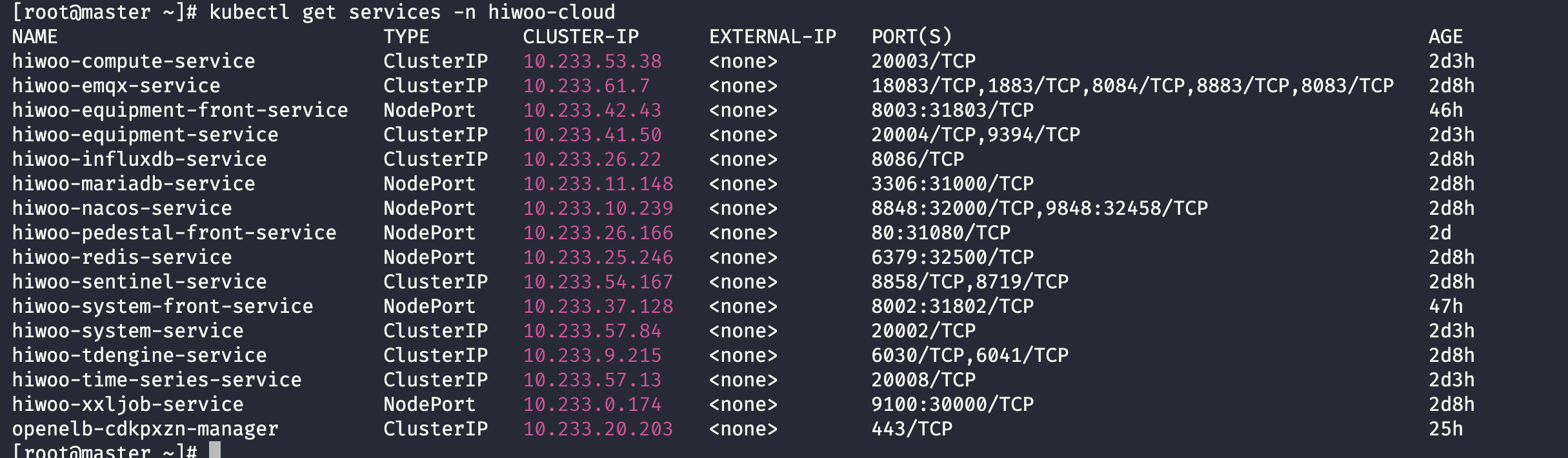
基于Kubesphere容器云平台物联网云平台Devops实践
基于Kubesphere容器云平台物联网云平台Devops实践 项目背景 公司是做工业物联网相关业务的,现业务是云平台,技术栈 后端为 Springboot2.7JDK11 ,前端为 Vue3Ts,需要搭建自动化运维平台以实现业务代码自动部署上线,…...
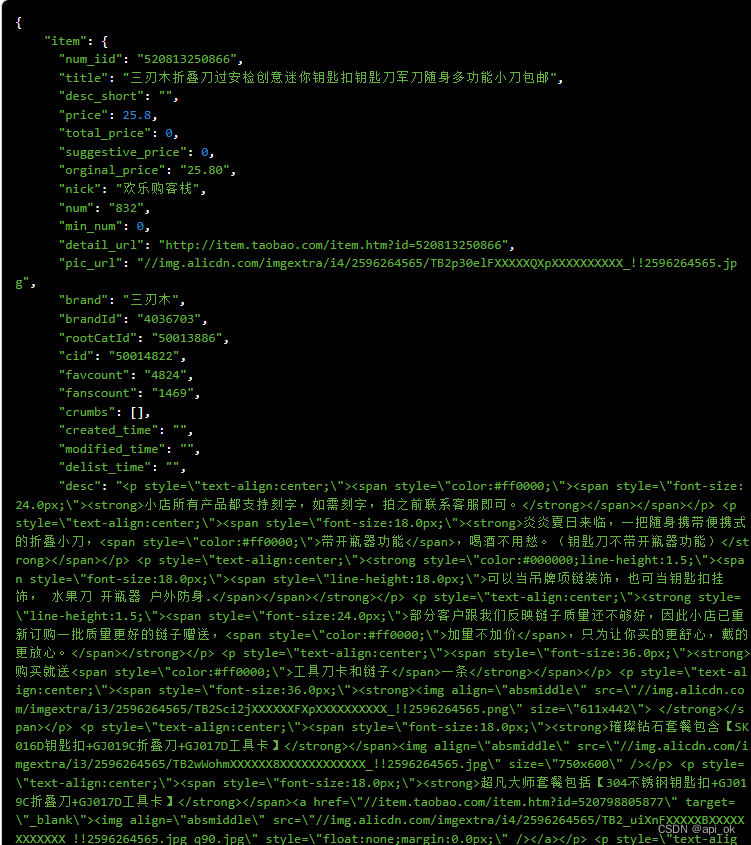
淘宝商品详情页API接口|tb获取商品主图接口
淘宝的 API 开发接口,我们需要做下面几件事情。 1)开放平台注册开发者账号; 2)然后为每个淘宝应用注册一个应用程序键(App Key) ; 3)下载淘宝 API 的 SDK 并掌握基本的 API 基础知识和调用&a…...
JAVA面试笔记
JAVA就业课程 面试整体流程 1.1 简单的自我介绍 我是xxxx,工作xxx年.我先后在xxxx公司、yyyy公司工作。先后做个xxxx项目、yyyy项目。 1.2 你简单介绍一下xxxx项目 为了解决xxxx问题,开发了一套xxxx系统,该系统主要有那些部分组成。简单介绍项目的整体架…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
