【数据结构】数组和字符串(四):特殊矩阵的压缩存储:稀疏矩阵——三元组表
文章目录
- 4.2.1 矩阵的数组表示
- 4.2.2 特殊矩阵的压缩存储
- a. 对角矩阵的压缩存储
- b~c. 三角、对称矩阵的压缩存储
- d. 稀疏矩阵的压缩存储——三元组表
- 结构体
- 初始化
- 元素设置
- 打印矩阵
- 主函数
- 输出结果
- 代码整合
4.2.1 矩阵的数组表示
【数据结构】数组和字符串(一):矩阵的数组表示
4.2.2 特殊矩阵的压缩存储
矩阵是以按行优先次序将所有矩阵元素存放在一个一维数组中。但是对于特殊矩阵,如对称矩阵、三角矩阵、对角矩阵和稀疏矩阵等, 如果用这种方式存储,会出现大量存储空间存放重复信息或零元素的情况,这样会造成很大的空间浪费。为节约存储空间和算法(程序)运行时间,通常会采用压缩存储的方法。
- 对角矩阵:指除了主对角线以外的元素都为零的矩阵,即对 任意 i ≠ j (1≤ i , j ≤n),都有M(i, j)=0。由于只有主对角线上有非零元素,只需存储主对角线上的元素即可。
- 三角矩阵:指上三角或下三角的元素都为零的矩阵。同样地,只需存储其中一部分非零元素,可以节省存储空间。
- 对称矩阵:指矩阵中的元素关于主对角线对称的矩阵。由于对称矩阵的非零元素有一定的规律,可以只存储其中一部分元素,从而减少存储空间。
- 稀疏矩阵:指大部分元素为零的矩阵。传统的按行优先次序存储方法会浪费大量空间来存储零元素,因此采用压缩存储的方法更为合适。常见的压缩存储方法有:压缩稠密行(CSR)、压缩稠密列(CSC)、坐标列表(COO)等。
a. 对角矩阵的压缩存储
【数据结构】数组和字符串(二):特殊矩阵的压缩存储:对角矩阵——一维数组
b~c. 三角、对称矩阵的压缩存储
【数据结构】数组和字符串(三):特殊矩阵的压缩存储:三角矩阵、对称矩阵——一维数组
d. 稀疏矩阵的压缩存储——三元组表
对于稀疏矩阵的压缩存储,由于非零元素的个数远小于零元素的个数,并且非零元素的分布没有规律,无法简单地利用一维数组和映射公式来实现压缩存储。针对稀疏矩阵,通常采用特定的数据结构来进行压缩存储,以减少存储空间的占用。
一种常见的稀疏矩阵压缩存储方法是使用"三元组"表示法,也称为COO(Coordinate)格式,只存储非零元素的值以及它们的行列坐标。通过使用三元组(Triplet)来表示非零元素的位置和值,每个三元组包含三个信息:非零元素的行索引、非零元素的列索引以及非零元素的值。
结构体
typedef struct {int row;int col;int value;
} Triple;typedef struct {Triple data[MAX_SIZE];int rows;int cols;int length;
} TripletTable;
定义了两个结构体:Triple 和 TripletTable。
Triple结构体表示稀疏矩阵的非零元素,包含三个字段:row表示行号,col表示列号,value表示元素的值。TripletTable结构体用于存储稀疏矩阵的数据,包含一个data数组用于存储非零元素的Triple结构体,以及rows、cols和length字段分别表示矩阵的行数、列数和非零元素的数量。
初始化
void initTable(TripletTable* table, int rows, int cols) {table->rows = rows;table->cols = cols;table->length = 0;
}
initTable 函数用于初始化 TripletTable 结构体,指定矩阵的行数和列数,并将 length 字段置为 0。
元素设置
void insertElement(TripletTable* table, int row, int col, int value) {if (table->length >= MAX_SIZE) {printf("Table is full. Cannot insert more elements.\n");return;}Triple* element = &(table->data[table->length]);element->row = row;element->col = col;element->value = value;table->length++;
}
insertElement 函数用于向稀疏矩阵中插入一个元素,传入参数为行号、列号和元素的值。
- 函数首先检查当前非零元素的数量是否已达到上限
MAX_SIZE- 如果达到上限则输出错误信息并返回。
- 否则,将新元素插入到
data数组的末尾,并更新length字段。
打印矩阵
void displayTable(TripletTable* table) {int matrix[table->rows][table->cols];for (int i = 0; i < table->rows; i++) {for (int j = 0; j < table->cols; j++) {matrix[i][j] = 0;}}printf("Row\tColumn\tValue\n");for (int i = 0; i < table->length; i++) {Triple* element = &(table->data[i]);printf("%d\t%d\t%d\n", element->row, element->col, element->value);matrix[element->row][element->col] = element->value;}printf("Matrix:\n");for (int i = 0; i < table->rows; i++) {for (int j = 0; j < table->cols; j++) {printf("%d\t", matrix[i][j]);}printf("\n");}
}
displayTable 函数用于显示稀疏矩阵的内容:
- 创建一个与稀疏矩阵相同大小的二维数组
matrix,并将其所有元素初始化为 0; - 遍历
data数组中的非零元素,输出每个元素的行号、列号和值,并将相应位置的matrix数组元素更新为对应的值; - 输出整个矩阵的内容。
主函数
int main() {TripletTable table;initTable(&table, 3, 3);insertElement(&table, 0, 0, 1);insertElement(&table, 0, 1, 2);insertElement(&table, 1, 1, 3);insertElement(&table, 2, 2, 4);displayTable(&table);return 0;
}
- 创建一个
TripletTable结构体table,并使用initTable函数初始化它,指定矩阵的行数和列数为3。 - 调用
insertElement函数向table中插入四个非零元素,分别位于 (0, 0)、(0, 1)、(1, 1) 和 (2, 2) 位置。 - 通过调用
displayTable函数,打印出稀疏矩阵的内容和对应的完整矩阵表示。
输出结果
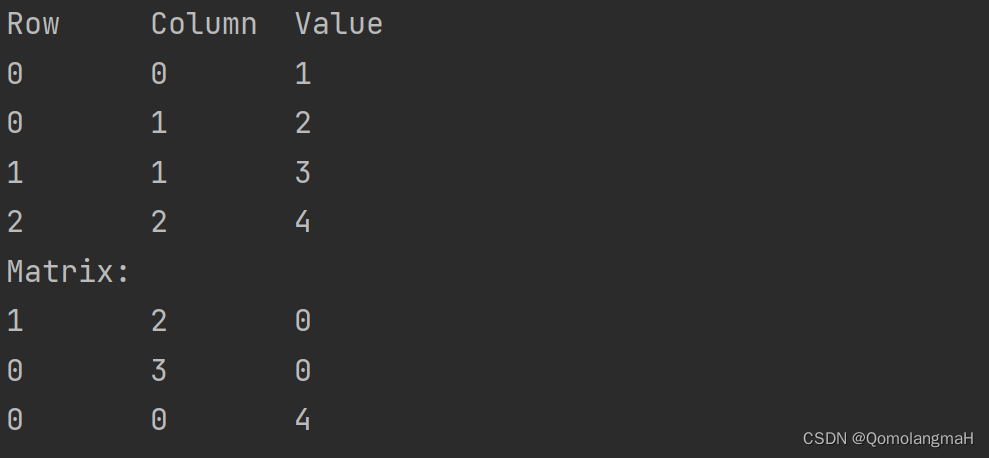
代码整合
#include <stdio <stdio.h>
#include <stdlib#include <stdlib.h>typedef struct {int row;int col;int value;
} Element;typedef struct {int rows;int cols;int numElements;Element* elements;
} SparseMatrix;SparseMatrix* createSparseMatrix(int rows, int cols, int numElements) {SparseMatrix* matrix = (SparseMatrix*)malloc(sizeof(SparseMatrix));matrix->rows = rows;matrix->cols = cols;matrix->numElements = numElements;matrix->elements = (Element*)malloc(numElements * sizeof(Element));return matrix;
}void destroySparseMatrix(SparseMatrix* matrix) {free(matrix->elements);free(matrix);
}void setElement(SparseMatrix* matrix, int row, int col, int value) {if (row >= matrix->rows || col >= matrix->cols) {printf("Error: Invalid row or column index.\n");return;}int index = row * matrix->cols + col;matrix->elements[index].row = row;matrix->elements[index].col = col;matrix->elements[index].value = value;
}int getElement(SparseMatrix* matrix, int row, int col) {if (row >= matrix->rows || col >= matrix->cols) {printf("Error: Invalid row or column index.\n");return 0;}int index = row * matrix->cols + col;return matrix->elements[index].value;
}int main() {int rows = 3;int cols = 3;int numElements = 4;SparseMatrix* matrix = createSparseMatrix(rows, cols, numElements);setElement(matrix, 0, 0, 1);setElement(matrix, 0, 2, 2);setElement(matrix, 1, 1, 3);setElement(matrix, 2, 2, 4);printf("Matrix:\n");for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {int value = getElement(matrix, i, j);printf("%d ", value);}printf("\n");}destroySparseMatrix(matrix);return 0;
}
相关文章:

【数据结构】数组和字符串(四):特殊矩阵的压缩存储:稀疏矩阵——三元组表
文章目录 4.2.1 矩阵的数组表示4.2.2 特殊矩阵的压缩存储a. 对角矩阵的压缩存储b~c. 三角、对称矩阵的压缩存储d. 稀疏矩阵的压缩存储——三元组表结构体初始化元素设置打印矩阵主函数输出结果代码整合 4.2.1 矩阵的数组表示 【数据结构】数组和字符串(一ÿ…...

为什么POST请求经常发送两次?
大多数初级前端程序员,在通过浏览器F12的调试工具调试网络请求时,可能都会有一个发现,在进行POST请求时,明明代码里只请求了一次,为什么network里发送了两次呢,难道我代码出bug了?带着疑问点开第…...

打破总分行数据协作壁垒,DataOps在头部股份制银行的实践|案例研究
从银行开始建设数据仓库至今已近20年,当前各银行机构在数据能力建设中面临诸多困扰:如何保证数据使用时的准确性?如何让数据敏捷响应业务变化?如何让更多的业务人员使用数据? 这些问题极大影响了经营指标的达成与业务…...
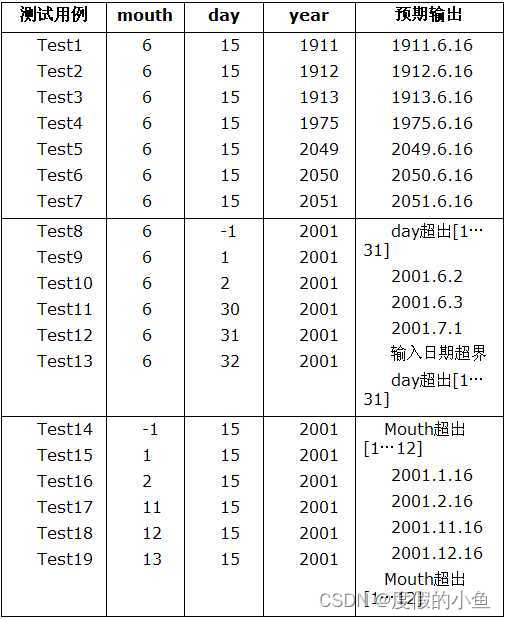
测试用例的设计方法(全):边界值分析方法
一.方法简介 1.定义:边界值分析法就是对输入或输出的边界值进行测试的一种黑盒测试方法。通常边界值分析法是作为对等价类划分法的补充,这种情况下,其测试用例来自等价类的边界。 2.与等价划分的区别 1)边界值分析不是从某等价类中随便挑…...
酷开科技 | 酷开系统沉浸式大屏游戏更解压!
随着家庭娱乐需求日益旺盛,越来越多的家庭消费者和游戏玩家开始追求大屏游戏带来的沉浸感。玩家在玩游戏的时候用大屏能获得更广阔的视野和更出色的视觉包围感,因此用大屏玩游戏已经成为了一种潮流。用酷开系统玩大屏游戏,过瘾又刺激…...
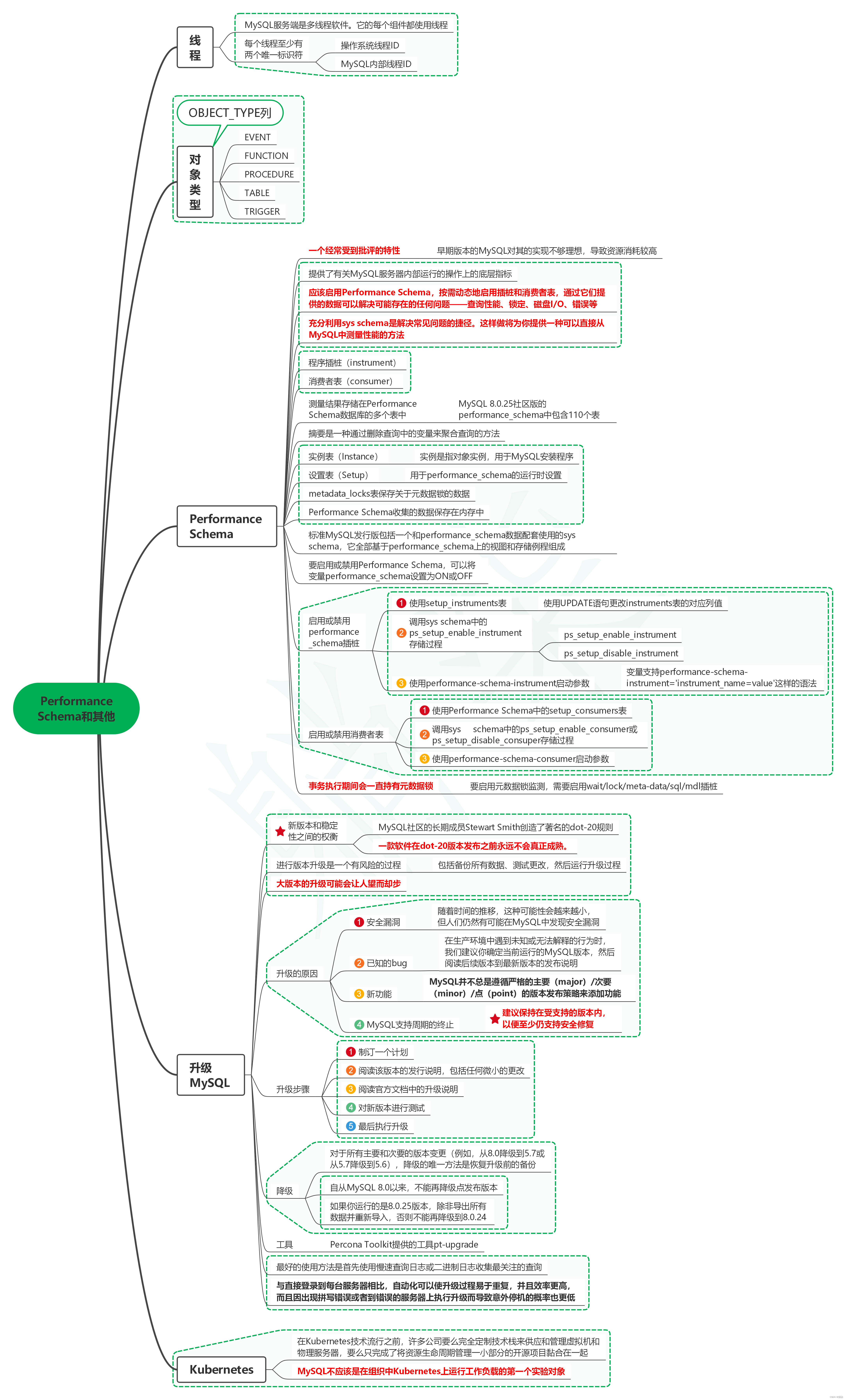
读高性能MySQL(第4版)笔记20_Performance Schema和其他
1. 线程 1.1. MySQL服务端是多线程软件。它的每个组件都使用线程 1.2. 每个线程至少有两个唯一标识符 1.2.1. 操作系统线程ID 1.2.2. MySQL内部线程ID 2. 对象类型 2.1. OBJECT_TYPE列 2.2. EVENT 2.3. FUNCTION 2.4. PROCEDURE 2.5. TABLE 2.6. TRIGGER 3. Perfor…...
《二》)
spring cloud Eureka集群模式搭建(IDEA中运行)《二》
上一篇集群配置文件完善 上一篇博客,想必大家都学会了Eureka集群模式的搭建和运行,针对上一篇的配置文件进行了优化,在这里分享给大家。上一篇主要有3个配置文件,分别对应3个不同的服务,这种形式配置文件分别写在了不…...

大模型(LLM)在电商推荐系统的探索与实践
本文对LLM推荐的结合范式进行了梳理和讨论,并尝试将LLM涌现的能力迁移应用在推荐系统之中,利用LLM的通用知识来辅助推荐,改善推荐效果和用户体验。 背景 电商推荐系统(Recommend System,RecSys)是一种基于…...
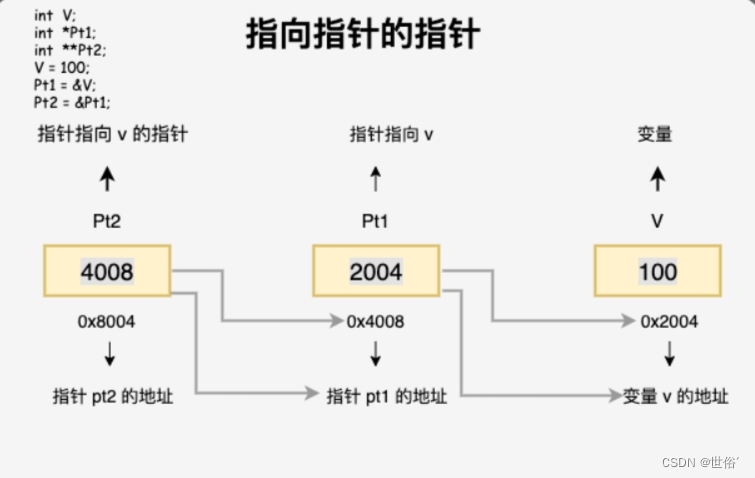
C语言之指针详解
目录 地址 指针的定义和使用 数组与指针的区别与联系 字符串与指针的用法 C 中的 NULL 指针 指针的算术运算 指向指针的指针 传递指针给函数 从函数返回指针 在学习指针之前,我们先弄清楚一个概念: 地址 地址在计算机内存中是一个唯一的标识符…...
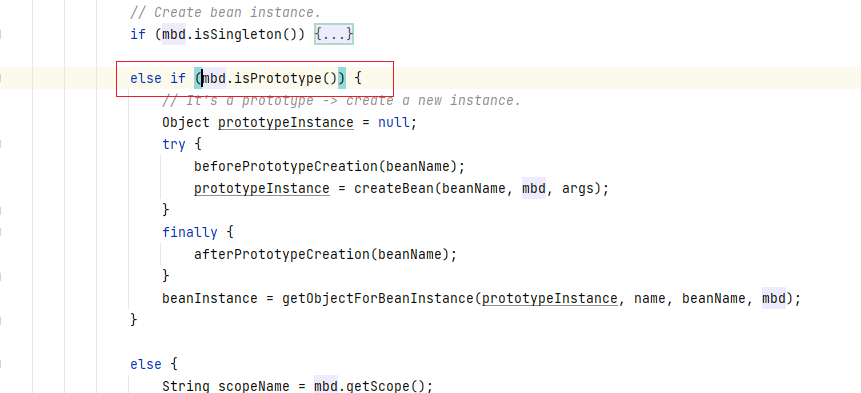
【Java笔记+踩坑】设计模式——原型模式
导航: 【Java笔记踩坑汇总】Java基础JavaWebSSMSpringBootSpringCloud瑞吉外卖/黑马旅游/谷粒商城/学成在线设计模式面试题汇总性能调优/架构设计源码-CSDN博客 目录 零、经典的克隆羊问题(复制10只属性相同的羊) 一、传统方案࿱…...

Flutter GetX使用详解
介绍 GetX是一款功能强大且轻量级的Flutter状态管理和路由管理库。它提供了一种简单而强大的方式来构建Flutter应用程序,无需大量的模板代码。GetX不仅提供了状态管理和路由管理,还包括其他实用工具,如国际化和依赖注入。 在本文中…...

【ARM Coresight 系列文章 3.3 - ARM Coresight SWD 协议详细介绍】
文章目录 1.1 SWD 协议框图1.2 读/写时序及命令1.2.1 SWD 时序1.2.2 SWD 命令详情1.3 芯片探测1.3.1 获取芯片 ID1.4 读/写操作1.1 SWD 协议框图 SWD协议可以配置SoC内部几乎所有的寄存器。时钟信号由SWCLK 管脚输入,数据信号从SWDIO管脚输入输出。首先 HOST 对SW-DP 进行操作…...

作为开发者,可视化开发工具了解一下
你是否为编程世界的各种挑战感到头痛?想要以更高效、简单的方式开发出专业级的项目? JNPF低代码工具正是你苦心寻找的产品!它是一款专为稍微懂一点点编程思想的入门级人员设计的神奇工具,集成了丰富的功能和组件,让你轻…...

Python:实现日历功能
背景 日常生活中,每天都要用到日历,日历成为我们生活中的必需品,那么如何制作日历呢,其实方法有很多,可以直接在excel中制作,也可以手画等等。 学习过编程的朋友,能否想到用Python编写一…...
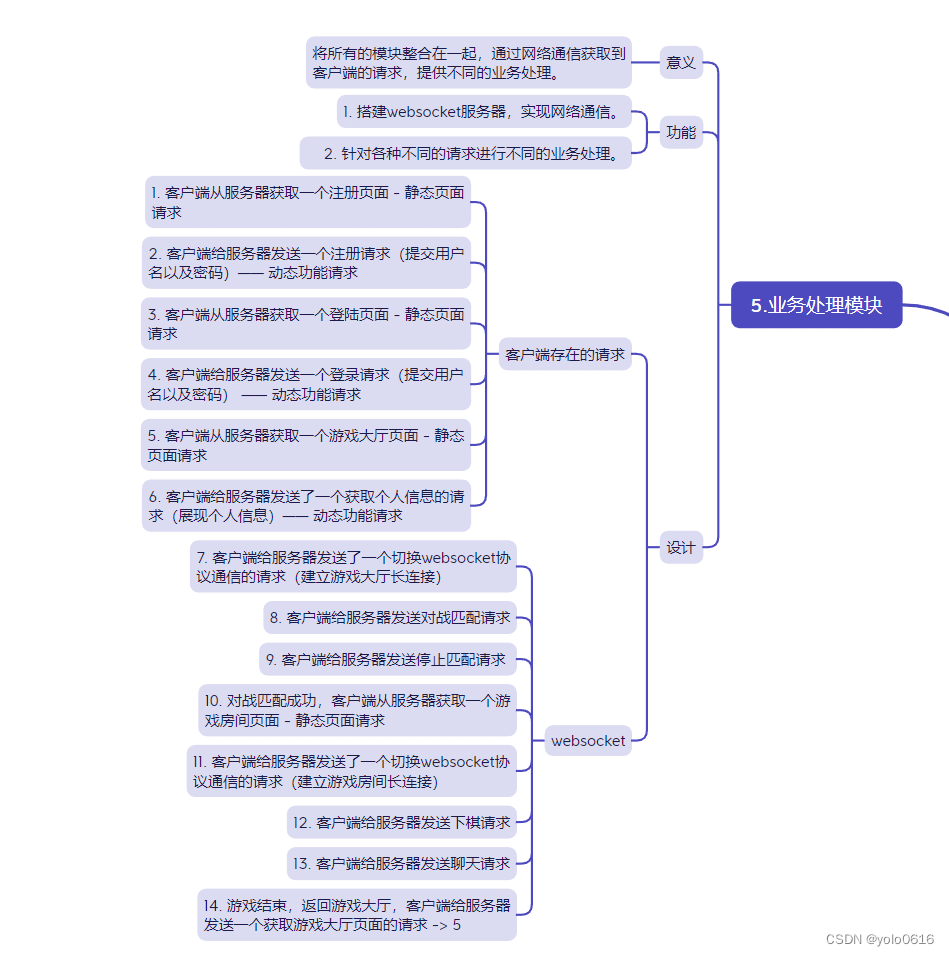
2.9.C++项目:网络版五子棋对战之业务处理模块的设计
文章目录 一、意义二、功能三、管理(一)客户端请求(二)websocket 四、框架五、完整代码 一、意义 将所有的模块整合在一起,通过网络通信获取到客户端的请求,提供不同的业务处理。 服务器模块,是…...

springboot actuator 常用接口
概述 微服务作为一项在云中部署应用和服务的新技术是当下比较热门话题,而微服务的特点决定了功能模块的部署是分布式的,运行在不同的机器上相互通过服务调用进行交互,业务流会经过多个微服务的处理和传递,在这种框架下࿰…...

知识点滴 - Email地址不区分大小写
电子邮件地址本身对字符大小写不敏感。这意味着实际的电子邮件地址,如 "exampleemail.com",并不区分字母的大小写。无论你输入的是大写字母还是小写字母,它仍然会到达同一个电子邮件账户。例如,如果您的电子邮件地址是 …...
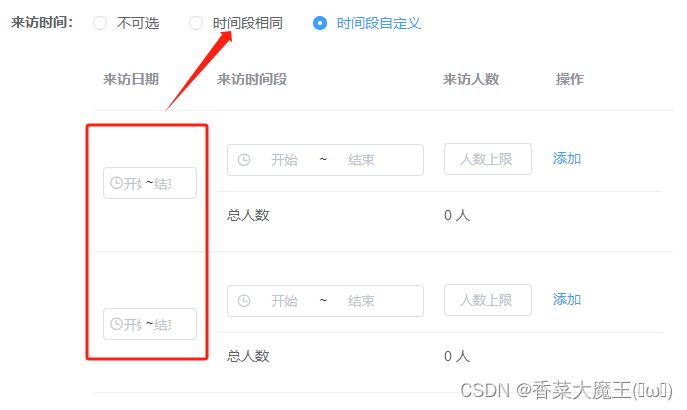
同一个页面同一区域两个el-table在v-if下样式重叠问题
🍉正常情况下在radio切换时两个表格的样式应如下 🍉实际上用v-if显示时会出现以下问题(本该属于时间段相同模块的表格却出现在时间段自定义的表格中) 🍉解决方案: 🍃一、将v-if替换成v-show(…...

ExoPlayer架构详解与源码分析(6)——MediaPeriod
系列文章目录 ExoPlayer架构详解与源码分析(1)——前言 ExoPlayer架构详解与源码分析(2)——Player ExoPlayer架构详解与源码分析(3)——Timeline ExoPlayer架构详解与源码分析(4)—…...

【开题报告】基于Spring Boot的课程在线预约系统的设计与实现
1.引言 随着互联网的发展,线上教育和课程培训变得越来越普遍。然而,很多学生在选择课程时面临一些困扰,例如如何找到适合自己的课程,如何与老师进行预约等。因此,设计一个基于Spring Boot的课程在线预约系统具有重要的…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
