VO,BO,PO,DO,DTO,AO的区别
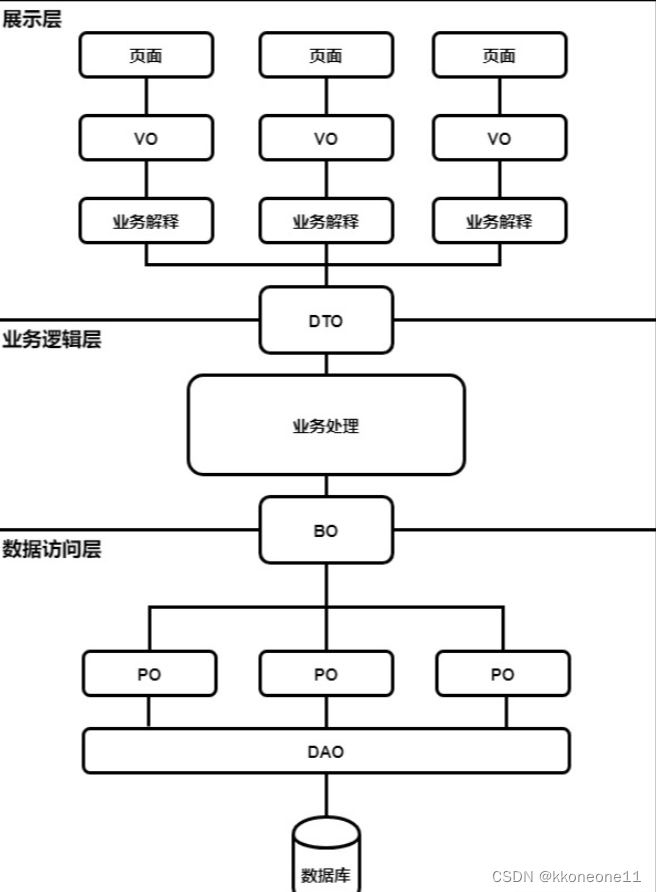
DTO(Data Transfer Object)数据传输对象
这个传输通常指的前后端之间的传输
1.在前端的时候:
存在形式通常是js里面的对象(也可以简单理解成json),也就是通过ajax请求的那个数据体
2.在后端的时候:
存在形式是java对象,也就是在controller里面定义的,通常在后端不需要关心怎么从json转成java对象的,这个都是由一些成熟的框架转化了,比如spring框架
这也是图片里它可以两层都占的原因。
DTO本身的一个隐含的意义是要能够完整的表达一个业务模块的输出,通常用于不同服务或服务不同分层之间的数据传输。如果两个服务不能互相独立那么之间传输的数据就不能叫DTO。
VO(View Object)表现对象
VO主要的存在形式就是js里面的对象(也可以简单理解成json),VO就是前端展示用的数据
PO(Persistant Object)持久对象
简单说PO就是数据库中的记录,一个PO的数据结构对应着库中表的结构,表中的一条记录就是一个PO对象。表示数据库中的一条记录映射成的 java 对象。PO 仅仅用于表示数据,没有任何数据操作。
BO(Business Object)业务对象
BO就是PO的组合,对多个PO对象的封装,形成一个业务逻辑。BO 包括了业务逻辑,常常封装了对 DAO、RPC 等的调用(因此除了setter和getter外还有自己的调用方法),可以进行 PO 与 VO/DTO 之间的转换。通常位于业务层,是被上层的服务层调用的。
比如PO1是交易记录,PO2是登录记录,PO3是商品浏览记录。那么BO就是人网站行为对象。除了外
AO( Application Object)应用对象
在Web层与Service层之间抽象的复用对象模型,极为贴近展示层,复用度不高。
POJO(Plain ordinary java object) 简单java对象
一个POJO持久化以后就是PO;直接用它传递、传递过程中就是DTO;直接用来对应表示层就是VO。
DO( Data Object)领域对象
通过DAO层向上传输数据源对象,就是从现实世界中抽象出来的有形或无形的业务实体。一般和数据中的表结构对应
DTO和VO区别
通常情况下字段基本一致,但DTO更多是VO(一个实体类如User类)的一个拓展和补充,也可以是VO是实体类(User类)的拓展(在代码业务开发的时候)。当一张表有20个字段,即PO有20个属性。但页面展示我们只需要5个字段。客户端用WEB service来获取数据,没有必要把整个PO对象传递到客户端,这时我们就可以用只有这5个属性的DTO来传递结果到客户端,这样也不会暴露服务端表结构.到达客户端以后,如果用这个对象来对应界面显示,那此时它的身份就转为VO.
参考文章
一篇文章讲清楚VO,BO,PO,DO,DTO的区别 - 知乎 (zhihu.com)
相关文章:

VO,BO,PO,DO,DTO,AO的区别
DTO(Data Transfer Object)数据传输对象 这个传输通常指的前后端之间的传输 1.在前端的时候: 存在形式通常是js里面的对象(也可以简单理解成json),也就是通过ajax请求的那个数据体 2.在后端的时候&…...

JavaSE学习笔记day15
零、 复习昨日 HashSet 不允许重复元素,无序 HashSet去重原理: 先比较hashcode,如果hashcode不一致,直接存储如果hashcode值一样,再比较equals如果equals值为true,则认为完全一样,不存储即去重否则存储 如果使用的是空参构造创建出的TreeSet集合,那么它底层使用的就是自然排序,…...
Spring Security认证研究
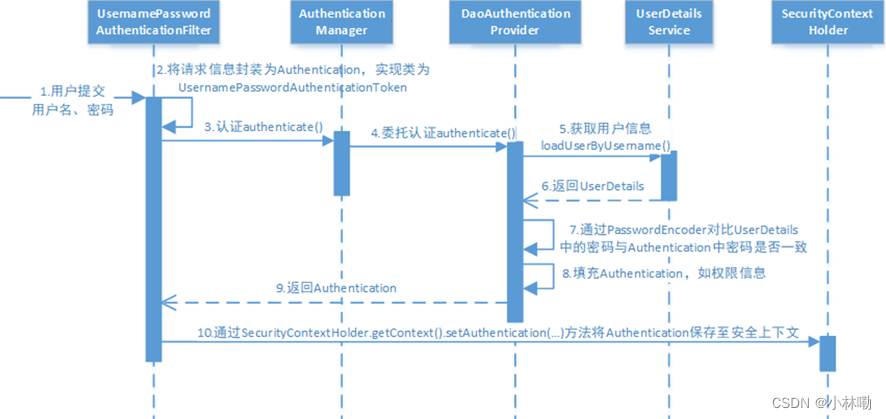
1.项目中认证的三种方式: 1.统一认证 认证通过由认证服务向给用户颁发令牌,相当于访问系统的通行证,用户拿着令牌去访问系统的资源。 2.单点登录,对于微服务项目,因为包含多个模块,所以单点登录就是使得用户…...

BigKey、布隆过滤器、分布式锁、红锁
文章目录 BigKey发现 BigKey如何删除BigKeyunlinkdelBigKey配置优化布隆过滤器布隆过滤器构建、使用、减少误判布隆过滤器二进制数组,如何处理删除?实现白名单 whitelistCustomer解决缓存穿透分布式锁依赖Redis 分布式锁代码使用红锁POM依赖yaml使用其他redis分布式锁容错率公…...
一文让你彻底理解Linux内核调度器进程优先级
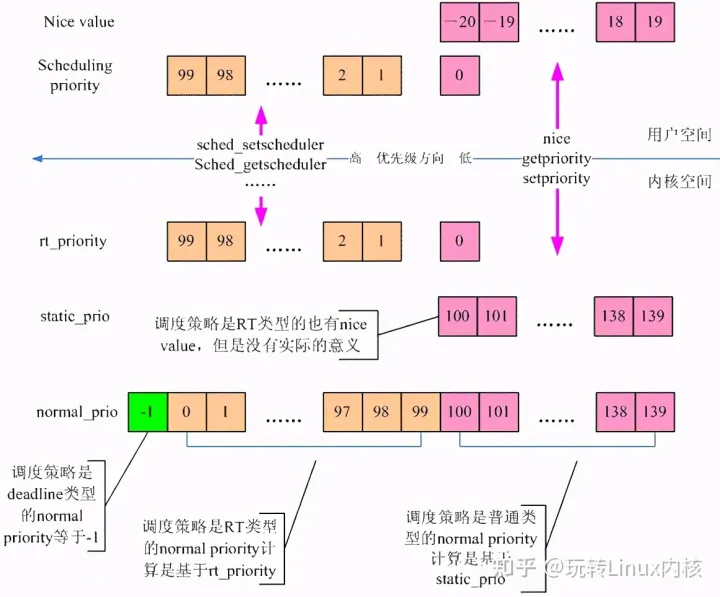
一、前言 本文主要描述的是进程优先级这个概念。从用户空间来看,进程优先级就是nice value和scheduling priority,对应到内核,有静态优先级、realtime优先级、归一化优先级和动态优先级等概念。我们希望能在第二章将这些相关的概念描述清楚。…...

Java 抽象类和接口
文章目录一、抽象类1. 抽象类定义2. 抽象类成员特点二、接口1. 接口概述2. 接口成员特点3. 类和接口的关系4. 抽象类和接口的区别5. 接口案例三、形参和返回值一、抽象类 1. 抽象类定义 在 Java 中,一个没有方法体的方法应该定义为抽象方法,而类中如果…...
三行代码让你的git记录保持整洁
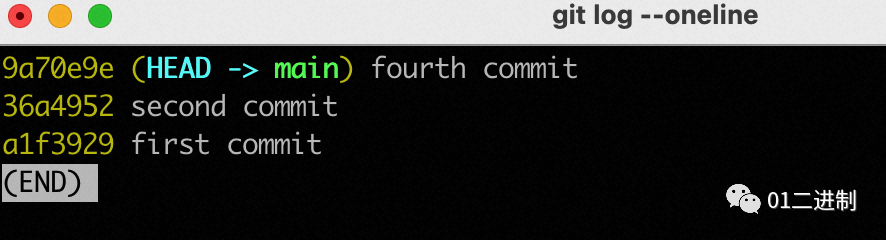
前言笔者最近在主导一个项目的架构迁移工作,由于迁移项目的历史包袱较重,人员合作较多,在迁移过程中免不了进行多分支、多次commit的情况,时间一长,git的提交记录便混乱不堪,随便截一个图形化的git提交历史…...

阿里巴巴内网 Java 面试 2000 题解析(2023 最新版)
前言 这份面试清单是今年 1 月份之后开始收集的,一方面是给公司招聘用,另一方面是想用它来挖掘在 Java 技术栈中,还有一些知识点是我还在探索的,我想找到这些技术盲点,然后修复它,以此来提高自己的技术水平…...
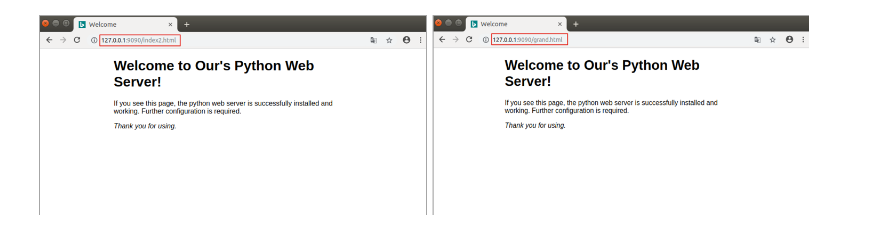
网络应用之静态Web服务器
静态Web服务器-返回固定页面数据学习目标能够写出组装固定页面数据的响应报文1. 开发自己的静态Web服务器实现步骤:编写一个TCP服务端程序获取浏览器发送的http请求报文数据读取固定页面数据,把页面数据组装成HTTP响应报文数据发送给浏览器。HTTP响应报文数据发送完…...

IndexDB 浏览器服务器
IndexDB 浏览器服务器 文章部分内容引用: https://www.ruanyifeng.com/blog/2018/07/indexeddb.html https://juejin.cn/post/7026900352968425486#heading-15 基本概念 数据库:IDBDatabase 对象对象仓库:IDBObjectStore 对象索引࿱…...
追梦之旅【数据结构篇】——详解C语言实现链队列
详解C语言实现链队列~😎前言🙌整体实现内容分析💞预备小知识🙌1.链队列头文件编写🙌2.链队列功能文件(Queue.c )编写:🙌1)初始化函数实现2)销毁函…...
SpringMVC - 13 - SpringMVC执行流程
文章目录1、SpringMVC常用组件2、DispatcherServlet初始化过程a>初始化WebApplicationContextb>创建WebApplicationContextc>DispatcherServlet初始化策略3、DispatcherServlet调用组件处理请求a>processRequest()b>doService()c>doDispatch()d>processDi…...

6091: 斐波那契数列
描述一个斐波那契序列,F(0) 0, F(1) 1, F(n) F(n-1) F(n-2) (n>2),根据n的值,计算斐波那契数F(n)。输入输入数据的第一行为测试用例的个数t,接下来为t行,每行为一个整数n(2≤n≤40)。输出…...
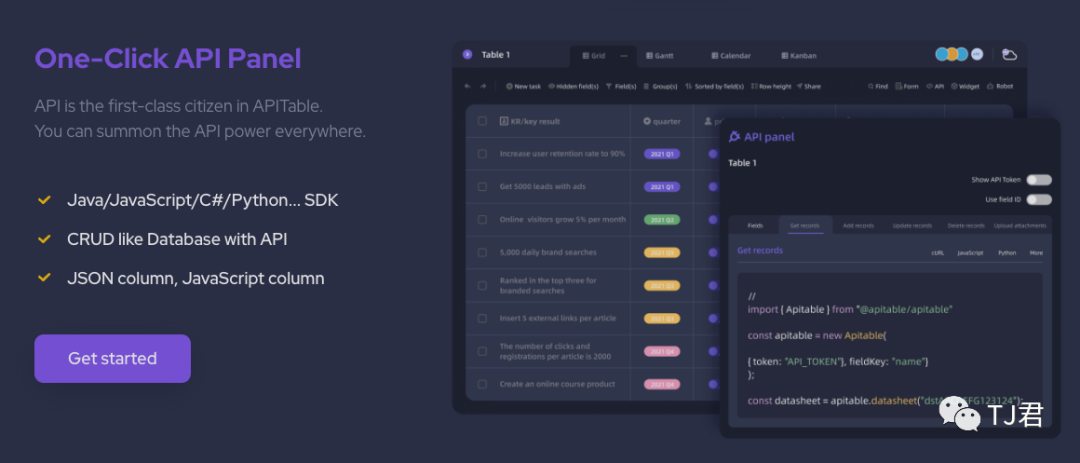
任何人均可上手的数据库与API搭建平台
编写API可能对于很多后端开发人员来说,并不是什么难事儿,但如果您主要从事前端功能,那么可能还是有一些门槛。 那么有没有工具可以帮助我们降低编写API的学习门槛和复杂度呢? 今天就来给大家推荐一个不错的开源工具:…...

Ubuntu(虚拟机)的Anaconda 及使用
安装Anaconda 使用firefox打开Ananconda网址Anaconda | The Worlds Most Popular Data Science Platform 下载后有.sh文件: Anaconda3-2022.10-Linux-x86_64.sh 进入所在目录打开终端并输入 $ bash Anaconda3-2022.10-Linux-x86_64.sh 然后开始安装。 对于给…...
Git ---- IDEA集成 GitHub
Git ---- IDEA集成 GitHub1. 设置 GitHub 账号2. 分享工程到 GitHub3. push 推送本地库到远程库4. pull 拉取远程库到本地库5. clone 克隆远程库到本地1. 设置 GitHub 账号 新版的 IDEA 选择之后会自动登录,就不需要设置 token 了。 如果是老版的 IDEA 的话&…...

opencv提取结构化文本总结
扫描文件表格识别 1.识别结构 situation1 有明确表格结构 1.纠正表格偏移角度(获取最大轮廓,计算最小的矩形,变换坐标截取矩形) 获取面积最大轮廓 _, contours, HIERARCHY cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2…...
JVM知识体系学习八:OOM的案例(承接上篇博文,可以作为面试中的案例)
文章目录前言一、概述二、案例二三、案例:方法区内存溢出1、代码:LambdaGC.java2、元空间内存溢出日志3、分析4、疑问*****四、案例:直接内存溢出问题(少见)(尽量不说)五、案例:栈内存溢出问题1…...
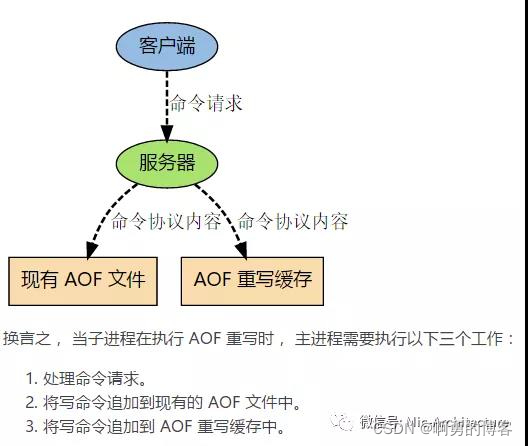
Redis的持久化方式
Redis支持两种方式的持久化,一种是RDB方式、另一种是AOF(append-only-file)方式,两种持久化方式可以单独使用其中一种,也可以将这两种方式结合使用。 •RDB:根据指定的规则“定时”将内存中的数据存储在硬…...

【unity游戏制作-mango的冒险】-4.场景二的镜头和法球特效跟随
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:unity游戏制作 ⭐mango的冒险场景二——镜头和法球特效跟随⭐ 文章目录⭐mango的冒险场景二——镜…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
