NPDP产品经理证书是什么行业的证书?
NPDP是一个跨行业的证书,它适用于各种不同类型和规模的组织。无论是制造业、服务业还是科技领域,都可以从NPDP认证中获益。

1. 制造业:
制造业涉及大量的产品开发和创新活动。从汽车制造到电子设备制造,从家居用品到航天航空,制造业中的专业人士可以通过获得NPDP认证,提高他们在产品开发过程中的能力,更好地满足市场需求,并推动公司的竞争力。
2、科技行业:
科技行业需要不断引入新产品和创新解决方案来应对快速变化的市场需求。软件开发、硬件设计、通信技术等领域的专业人员可以通过NPDP认证,掌握产品开发的最佳实践,加强项目管理能力,提高产品质量和交付效率。
3、服务业:
服务业也需要创新和新产品开发来满足客户需求并保持竞争优势。例如,银行业可以通过开发新的金融产品和服务增加客户价值;零售业可以通过新产品的设计和营销策略来吸引更多消费者。获得NPDP认证的服务业专业人士可以提升他们在产品开发和创新方面的能力,从而为公司带来更多机会和竞争优势。
总之,NPDP认证适用于各种行业和组织类型。它的目标是培养和认可专业人士在新产品开发领域的知识和技能,帮助他们推动创新、提高产品质量,并增强个人职业竞争力。不论所属行业如何,掌握新产品开发的最佳实践对于专业人士和组织的长期成功都至关重要。
相关文章:

NPDP产品经理证书是什么行业的证书?
NPDP是一个跨行业的证书,它适用于各种不同类型和规模的组织。无论是制造业、服务业还是科技领域,都可以从NPDP认证中获益。 1. 制造业: 制造业涉及大量的产品开发和创新活动。从汽车制造到电子设备制造,从家居用品到航天航空&…...
37 深度学习(一):查看自己显卡的指令|张量|验证集|分类问题|回归问题
文章目录 查看自己显卡的指令框架选什么张量的阶数验证集存在的意义分类问题一般的全连接的代码格式(板子)上面训练的详解一些省略梯度消失和梯度爆炸Dropout 回归问题一般回归的全连接的板子 batch-size超参数搜索策略 此系列的深度学习主要是理论性的介…...

用C语言解决三个整数比大小,x,y,z三个整数求最小整数,从键盘上输入3个不同的整数×,y,Z,请设计一个算法找出其中最小的数,并画出流程图。
用C语言解决三个整数比大小,x,y,z三个整数求最小整数,从键盘上输入3个不同的整数,y,Z,请设计一个算法找出其中最小的数,并画出流程图。 以下是一个用C语言解决三个整数比大小的示例代码: #include <stdio.h>int main() {i…...
操作系统进程调度算法的模拟实现(c语言版本)
前言:本文旨在分享如何使用c语言对操作系统中的部分进程调度算法进行模拟实现,以及算法描述的讲解,完整代码放在文章末尾,欢迎大家自行拷贝调用 目录 常见的调度算法 数据结构 先来先服务调度算法 算法模拟思路: …...

webbench压测工具
介绍 webbench是Linux下的一个网站压力测试工具,最多可以模拟3万个并发连接去测试网站的负载能力。 https://soft.lnmp.com/test/webbench/ 安装非常简单 tar zxvf webbench-1.5.tar.gz cd webbench-1.5 make && make install会在当前目录生成webbench可执…...

HarmonyOS 音频开发指导:使用 OpenSL ES 开发音频播放功能
OpenSL ES 全称为 Open Sound Library for Embedded Systems,是一个嵌入式、跨平台、免费的音频处理库。为嵌入式移动多媒体设备上的应用开发者提供标准化、高性能、低延迟的 API。HarmonyOS 的 Native API 基于Khronos Group开发的OpenSL ES 1.0.1 API 规范实现&am…...

docker搭建个人镜像仓库
docker搭建个人镜像仓库 安装registry mkdir docker-registry cd docker-registry mkdir registry mkdr auth vim docker-compose.ymldocker-compose.yml的内容如下: version: 3 services:registry:image: registrycontainer_name: registryvolumes:- ./registry…...
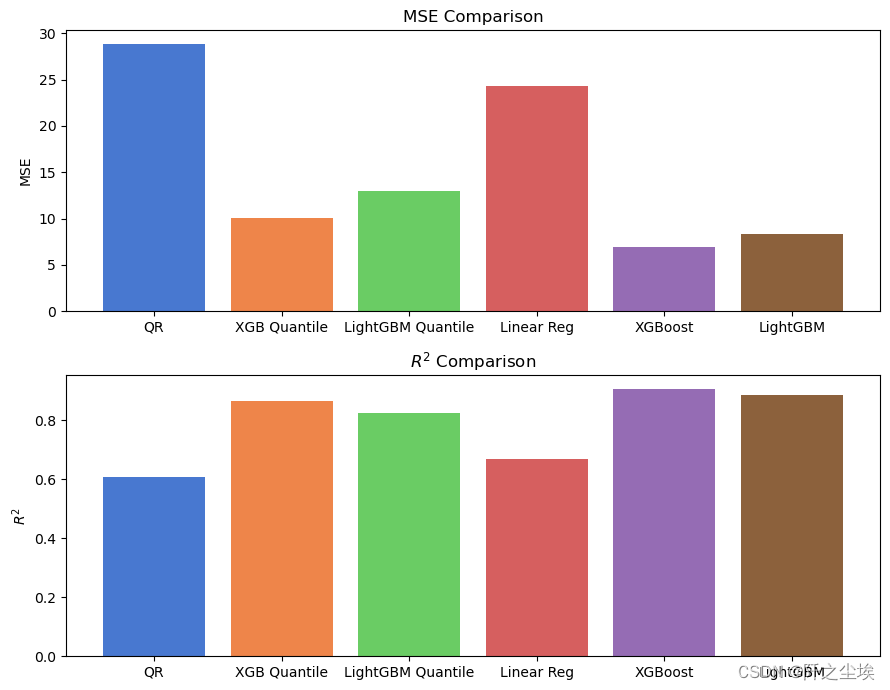
Python机器学习17——Xgboost和Lightgbm结合分位数回归(机器学习与传统统计学结合)
最近XGboost支持分位数回归了,我看了一下,就做了个小的代码案例。毕竟学术市场上做这种新颖的机器学习和传统统计学结合的方法还是不多,算的上创新,找个好数据集可以发论文。 代码实现 导入包 import numpy as np import pandas…...

C#编程学习
1. **C#简介**: - C#是一种现代的、面向对象的编程语言,由Microsoft开发。 - 它是.NET框架的一部分,用于开发Windows应用程序、Web应用程序和服务等。 2. **开发环境**: - 你可以使用Visual Studio或Visual Studio Code…...
)
关于vue 父级不使用子级某模块 (插槽替换)
父级: <template><div><MoreSupplements code"Xmgk" message"补充内容越多,越精准"><template #r-btn>xxx</template></MoreSupplements></div> </template> <script> import MoreSupplements fr…...

睿趣科技:抖音小店在哪里选品
随着抖音平台的日益火爆,越来越多的商家选择在抖音小店开设自己的店铺。然而,对于许多新手来说,如何选品却成为了一个难题。那么,抖音小店应该在哪里选品呢? 首先,我们可以从抖音平台上的热门商品入手。通过观察抖音上…...

量变引起质变:安卓改多了,就是自己的OS
最近小米也发布了自己的OS,其他也有厂家跟进。这是自华为鸿蒙之后,大家都说自己开发OS。对此,也是有很多争论的。 有人说,这些东西不都是安卓套壳或者改名吗?怎么就变成了自己的OS?这种观点对不对呢&#x…...

IDEA 之 在不更改操作系统用户名的情况下更改 ${USER} 变量?
如何在不更改操作系统用户名的情况下更改 IntelliJ IDEA 中的 ${USER} 变量 IDEA -> Help -> Edit Custom VM 添加如下内容 -Duser.nameusername这样在文件或者函数注释的时候会读取这个配置,而不会读取电脑登录用户名...
基于JAVA的天猫商场系统设计与实现,springboot+jsp,MySQL数据库,前台用户+后台管理,完美运行,有一万五千字论文
目录 演示视频 基本介绍 论文目录 系统截图 演示视频 基本介绍 基于JAVA的天猫商场系统设计与实现,springbootjsp,MySQL数据库,前台用户后台管理,完美运行,有一万五千字论文。 本系统在HTML和CSS的基础上…...
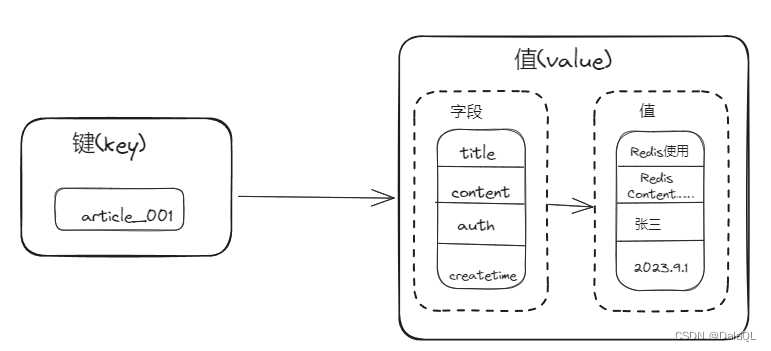
Redis学习
缓存定义 缓存是一个告诉数据交换的存储器,使用它可以快速的访问和操作数据。 常见缓存使用 本地缓存的常见使用:Spring Cache、MyBatis的缓存等 我的session存储和redis都放到缓存里面的,所有程序不管部署多少份,访问的都是r…...
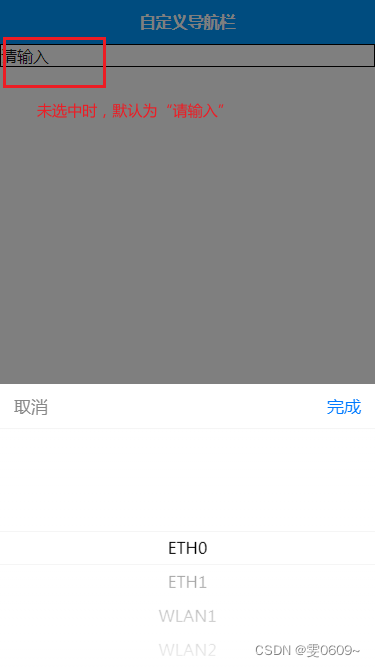
uni-app:实现picker下拉列表的默认值设置
效果 分析 1、在data中将index8的初始值设置为-1,表示未选择任何选项: index8: -1, //选择的下拉列表下标 2、在bindPickerChange8事件处理函数中添加条件判断。如果选择的值是-1,则将this.index8设置为"请输入",否则将…...
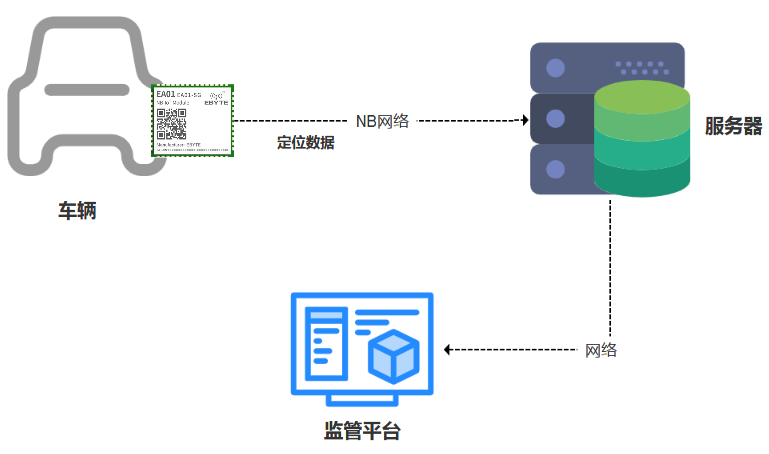
基于NB-iot技术实现财物跟踪的EA01-SG定位模块方案
NB-iot无线数传模块可做财物防盗窃器,让你的财物可定位跟踪! 随着社会的发展,公共资源及共享资源的蓬勃发展,对资产管理和资产追踪有了新的需求,如:某儿童玩具车在商场外面提供车辆乘坐游玩服务࿰…...

挑战吧,HarmonyOS应用开发工程师
一年一度属于工程师的专属节日1024,多重活动亮相啦~ 参与活动即有机会获得HUAWEI Freebuds 5i 耳机等精美礼品! 点击“阅读原文”查看更多活动详情!...
图论05-【无权无向】-图的广度优先BFS遍历-路径问题/检测环/二分图/最短路径问题
文章目录 1. 代码仓库2. 单源路径2.1 思路2.2 主要代码 3. 所有点对路径3.1 思路3.2 主要代码 4. 联通分量5. 环检测5.1 思路5.2 主要代码 6. 二分图检测6.1 思路6.2 主要代码6.2.1 遍历每个联通分量6.2.2 判断相邻两点的颜色是否一致 7. 最短路径问题7.1 思路7.2 代码 1. 代码…...
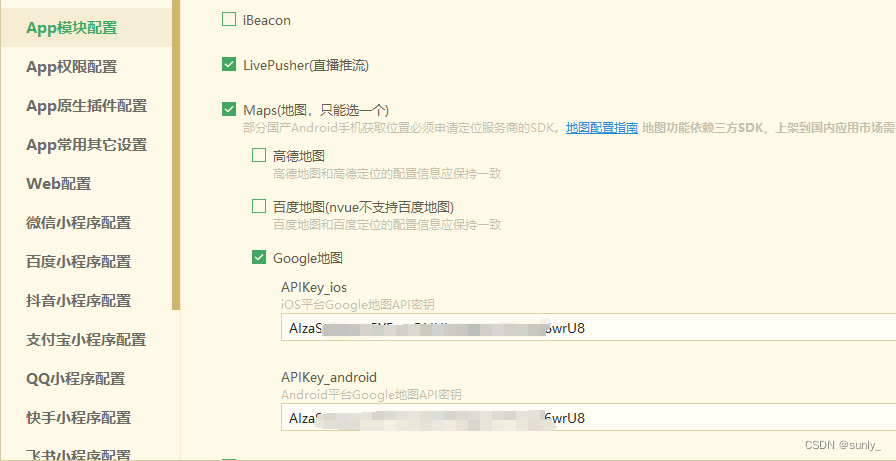
uniapp:谷歌地图,实现地图展示,搜索功能,H5导航
页面展示 APP H5 谷歌地图功能记录,谷歌key申请相对复杂一些,主要需要一些国外的身份信息。 1、申请谷歌key 以下是申请谷歌地图 API 密钥的流程教程: 登录谷歌开发者控制台:打开浏览器,访问 Google Cloud Platform Console。 1、创建或选择项目:如果你还没有创建项目…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
