2023NOIP A层联测18 划分
题目大意
对于一个长度为 n n n的 01 01 01字符串 S S S,请求出将其分为至少 k k k段,将每段看成二进制数求和后的最大值以及取到这个最大值的划分方案的数量。
输出最大值模 998244353 998244353 998244353后的值和划分方案的数量模 998244353 998244353 998244353后的值。
1 ≤ n , k ≤ 2 × 1 0 6 1\leq n,k\leq 2\times 10^6 1≤n,k≤2×106
题解
如果前 k k k位没有 1 1 1,则最优解一定是第一个 1 1 1之前所有间隔中选 k − 1 k-1 k−1个及以上的间隔(因为把最后一段形成的二进制数从中间分开一定会减小),可以用组合数来计算。如果一个 1 1 1都没有,则最优解就是 n − 1 n-1 n−1个间隔中选 k − 1 k-1 k−1个及以上的间隔。
如果不满足上面的条件,则最优解一定是选出一段长度为 n − k + 1 n-k+1 n−k+1子串,剩下的每一个数单独分一段。我们考虑比较两种划分方案的大小。
设第一种划分方案的 n − k + 1 n-k+1 n−k+1的串看成的二进制数为 v 1 v_1 v1,其余 k − 1 k-1 k−1段中 1 1 1的个数为 t 1 t_1 t1,第二种划分方案的 n − k + 1 n-k+1 n−k+1的串看成的二进制数为 v 2 v_2 v2,其余 k − 1 k-1 k−1段中 1 1 1的个数为 t 2 t_2 t2。当 v 1 > v 2 v_1>v_2 v1>v2时
- 如果 v 1 v_1 v1和 v 2 v_2 v2的前 n − k n-k n−k位相同,而 v 1 v_1 v1的最后一位为 1 1 1, v 2 v_2 v2的最后一位为 0 0 0,则 t 1 + 1 = t 2 t_1+1=t_2 t1+1=t2,两种划分方案的结果是相同的
- 如果 v 1 v_1 v1和 v 2 v_2 v2的前 n − k n-k n−k位存在不同,则设第一个不同的位为 t t t
- 如果 t 1 ≥ t 2 t_1\geq t_2 t1≥t2,则显然第一种方案更优
- 如果 t 1 < t 2 t_1<t_2 t1<t2,则我们将 S S S中的每个 1 1 1减去对答案的贡献 1 1 1,两种划分方案的大小关系不变。此时其余 k − 1 k-1 k−1段中的 1 1 1都不算贡献,最大段中每一个为 1 1 1的位 i i i的贡献为 2 i − 1 2^i-1 2i−1,那么两种方案中前 t − 1 t-1 t−1个位置的贡献相同,第一种方案中第 t t t位的贡献为 2 t − 1 2^t-1 2t−1,而第二种划分方案中第 t t t位为 0 0 0,之后的位之和小于等于 2 t − 1 2^t-1 2t−1,因为每个 1 1 1的贡献都被减去了 1 1 1,所以之后的位的贡献之和小于 2 t − 1 2^t-1 2t−1,得第一种方案更优
由此可得,以 1 , 2 , … , k 1,2,\dots,k 1,2,…,k开头,长度为 n − k + 1 n-k+1 n−k+1的串中,划分出的串为字典序最大的串的结果最优。如果字典序最大的串的最后一位为 1 1 1,前面 n − k n-k n−k位与其相同,最后一位为 0 0 0的串也是最优的。
那我们怎么求字典序最大的串呢?可以用二分哈希。从 1 1 1到 k k k枚举 i i i,设 l l l为以 1 1 1到 i − 1 i-1 i−1为起点的串中字典序最大的串的起点,那么对于当前的 i i i,我们要比较 l l l开头的串和 i i i开头的串的字典序的大小。那么,我们可以二分两个串最长的公共前缀,假设公共前缀为 1 1 1到 t t t,则 t + 1 t+1 t+1即为两个串中第一个不同的位置,比较这个位置的大小即可知道两个串的大小关系。用哈希可以 O ( 1 ) O(1) O(1)判断两个字符串是否相同,所以处理一个 i i i的时间复杂度是 O ( log n ) O(\log n) O(logn)的。
求出字典序最大的串之后,判断这个串的最后一位是否为 1 1 1。如果是的话,将 1 1 1改为 0 0 0,再判断以 1 , 2 , … , k 1,2,\dots,k 1,2,…,k开头,长度为 n − k + 1 n-k+1 n−k+1的串中是否有与这个修改后的串相同的,这同样可以用哈希来 O ( 1 ) O(1) O(1)比较。
最大值可以用字典序最大的串对应的二进制数加其余部分的 1 1 1的个数来得到,方案数可以在比较大小和是否相同的时候得到,那么这道题就解决了。
注意要特判 n = = k n==k n==k的情况,此时最大值为 S S S中 1 1 1的个数,方案数为 1 1 1。
注意代码中虽然使用了单哈希,但这样有一定可能将两个不同的串判断为相同的串(有可能,但可能性不大),所以最好使用双哈希。
时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=2000000;
const long long mod=998244353;
int n,k,len,sum[N+5];
long long ans1,ans2,p[N+5],pw[N+5],jc[N+5],ny[N+5];
char s[N+5];
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
void init(){jc[0]=1;pw[0]=1;for(int i=1;i<=N;i++){jc[i]=jc[i-1]*i%mod;pw[i]=pw[i-1]*2%mod;}ny[N]=mi(jc[N],mod-2);for(int i=N-1;i>=0;i--) ny[i]=ny[i+1]*(i+1)%mod;
}
long long C(int x,int y){return jc[x]*ny[y]%mod*ny[x-y]%mod;
}
long long hsh(int l,int r){return (p[r]-p[l-1]*pw[r-l+1]%mod+mod)%mod;
}
int gt(int i,int j){int l=1,r=len,mid;while(l<=r){mid=l+r>>1;if(hsh(i,i+mid-1)==hsh(j,j+mid-1)) l=mid+1;else r=mid-1;}return l-1;
}
int main()
{
// freopen("divide.in","r",stdin);
// freopen("divide.out","w",stdout);init();scanf("%d%d",&n,&k);len=n-k+1;scanf("%s",s+1);for(int i=1;i<=n;i++){sum[i]=sum[i-1]+s[i]-'0';p[i]=(p[i-1]*2+s[i]-'0')%mod;}if(!sum[n]){for(int i=k;i<=n;i++){ans2=(ans2+C(n-1,i-1))%mod;}printf("0 %lld",ans2);return 0;}if(k==n){printf("%lld 1",sum[n]);return 0;}if(sum[n-len+1]==0){int fst=1;while(s[fst]!='1') ++fst;ans1=hsh(fst,n);for(int i=k;i<=fst;i++){ans2=(ans2+C(fst-1,i-1))%mod;}printf("%lld %lld",ans1,ans2);return 0;}int l=1;ans2=1;for(int i=2;i+len-1<=n;i++){int vt=gt(l,i);if(vt==len) ++ans2;else if(s[l+vt]<s[i+vt]){l=i;ans2=1;}}if(s[l+len-1]=='1'){int hs=(hsh(l,l+len-1)-1)%mod;for(int i=1;i+len-1<=n;i++){if(hs==hsh(i,i+len-1)) ++ans2;}}ans1=hsh(l,l+len-1)+sum[l-1]+sum[n]-sum[l+len-1];printf("%lld %lld",ans1,ans2);return 0;
}
相关文章:

2023NOIP A层联测18 划分
题目大意 对于一个长度为 n n n的 01 01 01字符串 S S S,请求出将其分为至少 k k k段,将每段看成二进制数求和后的最大值以及取到这个最大值的划分方案的数量。 输出最大值模 998244353 998244353 998244353后的值和划分方案的数量模 998244353 998244…...

pc与android设备进行通信
首先:根据此博客 Android模拟器调试TCP通讯_.emulator_console_auth_token-CSDN博客 思考: 只在本机电脑中: 服务器IP地址设为为0.0.0.0,并开始监听,客户端IP地址127.0.0.1,192.168.1.114都可连接。 12…...

【网安大模型专题10.19】论文6:Java漏洞自动修复+数据集 VJBench+大语言模型、APR技术+代码转换方法+LLM和DL-APR模型的挑战与机会
How Effective Are Neural Networks for Fixing Security Vulnerabilities 写在最前面摘要贡献发现 介绍背景:漏洞修复需求和Java漏洞修复方向动机方法贡献 数据集先前的数据集和Java漏洞Benchmark数据集扩展要求数据处理工作最终数据集 VJBenchVJBench 与 Vul4J 的…...
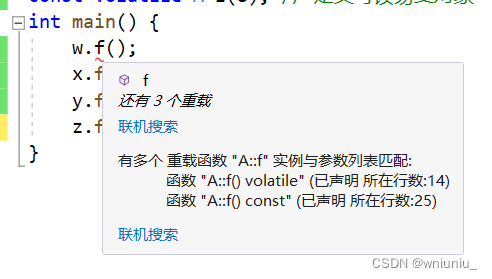
const 和 volatile 在实例成员函数的应用
const 和 volatile 的使用范围几乎没有限制 实例成员函数的参数后面可以出现 const 或 volatile,它们都用于修饰函数隐含参数 this 指向的对象 实例函数对象的参数表后面出现 const 说明this 所指向的对象是不能修改的只读对象 但是可以修改this所指向对象的非只读类…...
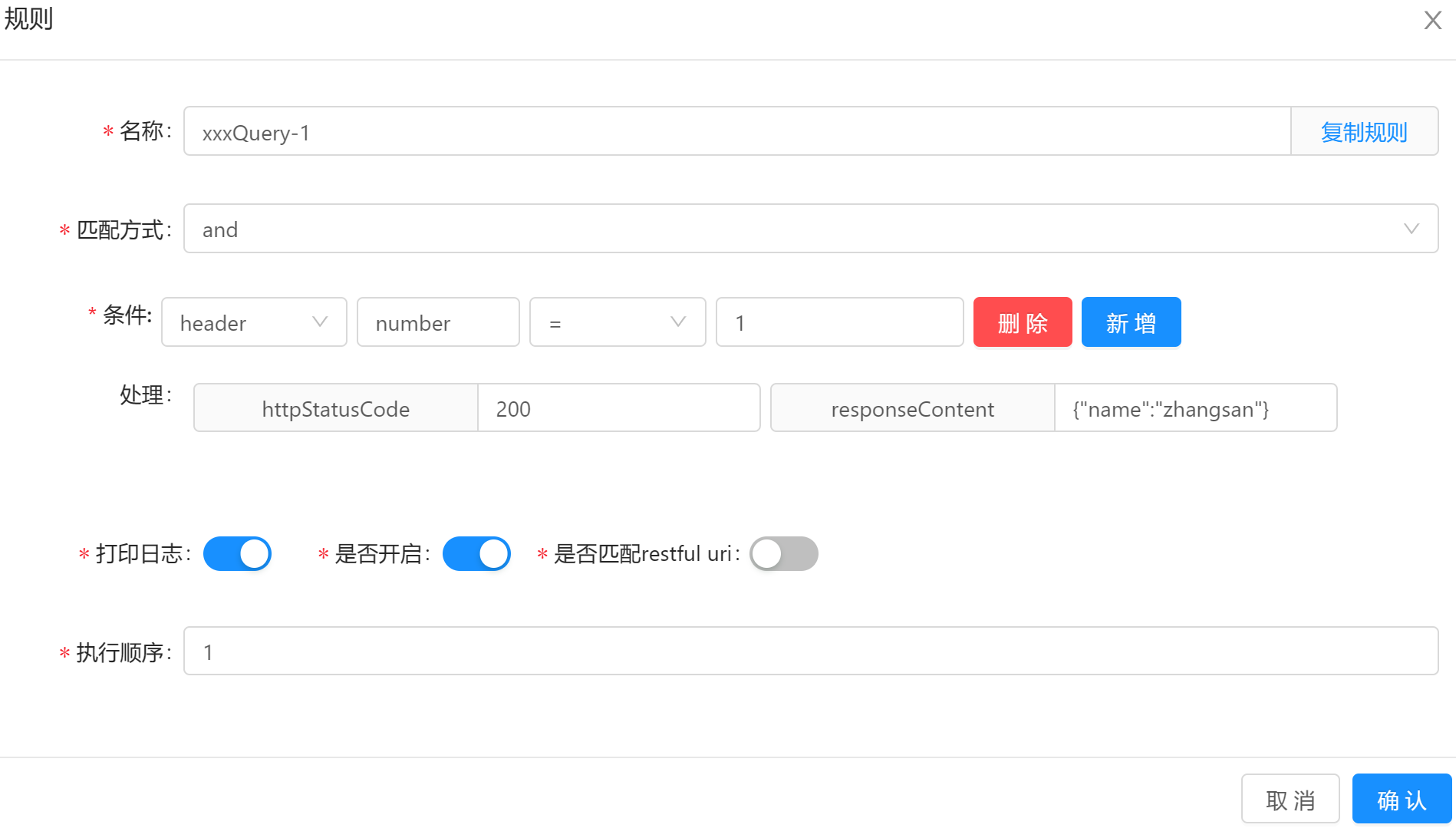
比Nginx测试桩更方便,ShenYu网关的Mock插件
有时候为了方便测试,我们需要模拟 HTTP 外部接口的返回结果。通常情况下,我们可以使用 Nginx 测试桩来实现这个目的。然而,Nginx 的使用门槛较高,可能对一些初级开发和测试人员来说有一定的难度。相比之下,Apache Shen…...
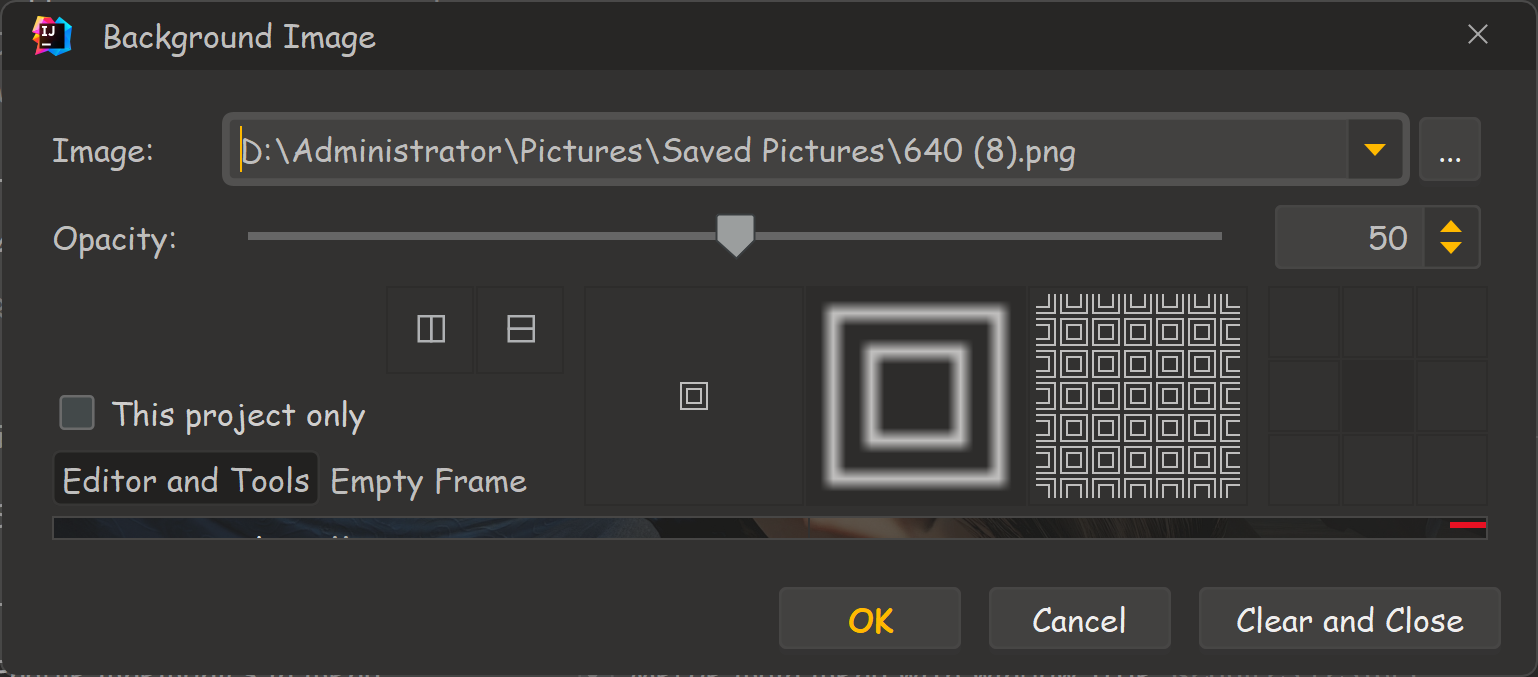
IDEA: 自用主题及字体搭配推荐
文章目录 1. 字体设置推荐2. 主题推荐3. Rainbow Brackets(彩虹括号)4. 设置背景图片 下面是我的 IDEA 主题和字体,它们的搭配效果如下: 1. 字体设置推荐 在使用 IntelliJ IDEA 进行编码和开发时,一个合适的字体设置可以提高你的工作效率和舒…...

Qt中的枚举变量,Q_ENUM,Q_FLAG以及Qt中自定义结构体、枚举型做信号参数传递
Qt中的枚举变量,Q_ENUM,Q_FLAG,Q_NAMESPACE,Q_ENUM_NS,Q_FLAG_NS以及其他 理论基础:一、Q_ENUM二、QMetaEnum三、Q_FLAG四、示例 Chapter1 Qt中的枚举变量,Q_ENUM,Q_FLAG,Q_NAMESPACE,Q_ENUM_NS,Q_FLAG_NS以及其他前言Q_ENUM的使用Q_FLAG的引入解决什么问题…...
【C++】priority_queue仿函数
今天我们来学习C中另一个容器适配器:优先级队列——priority_queue;和C一个重要组件仿函数: 目录 一、priority_queue 1.1 priority_queue是什么 1.2 priority_queue的接口 1.2.1 priority_queue使用举例 二、仿函数 三、关于priority…...

如何驾驭ChatGPT:掌控有效对话!
📢📢📢📣📣📣 哈喽!大家好,我是【一心同学】,一位上进心十足的【后端领域博主】!😜😜😜 ✨【一心同学】的写作风格&#x…...

LeetCode 面试题 16.03. 交点
文章目录 一、题目二、C# 题解 一、题目 给定两条线段(表示为起点 start {X1, Y1} 和终点 end {X2, Y2}),如果它们有交点,请计算其交点,没有交点则返回空值。 要求浮点型误差不超过 10^-6。若有多个交点(…...

【码银送书第九期】《ChatGPT 驱动软件开发:AI 在软件研发全流程中的革新与实践》
计算机技术的发展和互联网的普及,使信息处理和传输变得更加高效,极大地改变了金融、商业、教育、娱乐等领域的运作方式。数据分析、人工智能和云计算等新兴技术,也在不断地影响和改变着各个行业。 如今,我们正在见证人工智能技术的…...
Hadoop3.0大数据处理学习4(案例:数据清洗、数据指标统计、任务脚本封装、Sqoop导出Mysql)
案例需求分析 直播公司每日都会产生海量的直播数据,为了更好地服务主播与用户,提高直播质量与用户粘性,往往会对大量的数据进行分析与统计,从中挖掘商业价值,我们将通过一个实战案例,来使用Hadoop技术来实…...

华为机试题:HJ3 明明的随机数
目录 第一章、算法题1.1)题目描述1.2)解题思路与答案1.3)牛客链接 友情提醒: 先看文章目录,大致了解文章知识点结构,点击文章目录可直接跳转到文章指定位置。 第一章、算法题 1.1)题目描述 题目描述&…...

Python OpenCV将n×n的小图拼接成m×m的大图
Python OpenCV将nn的小图拼接成mm的大图 前言前提条件相关介绍实验环境n \times n的小图拼接成m \times m的大图代码实现 前言 由于本人水平有限,难免出现错漏,敬请批评改正。更多精彩内容,可点击进入Python日常小操作专栏、OpenCV-Python小…...
wkhtmltoimage/wkhtmltopdf 使用实践
1. 介绍 wkhtmltopdf/wkhtmltoimage 用于将简单的html页面转换为pdf或图片; 2.安装 downloads 2.1. mac os 下载64-bit 版本然后按照指示安装, 遇到 untrust developers 时,需要在 Settings -> Privacy 处信任下该安装包。 2.2. debian # 可用…...
Rclone连接Onedrive
一、Rclone介绍 Rclone是一款的命令行工具,支持在不同对象存储、网盘间同步、上传、下载数据。 我们这里连接的onedrive,其他网盘请查看官方文档。 注意: 需要先在Windows下配置好了,然后再将rclone配置文件复制到Linux的rclone配…...
RK356X/RK3588构建Ubuntu20.04根文件系统
文章目录 前言一、官网下载ubuntu-base二、挂载并构建文件系统2.1、配置构建文件系统环境2.2、编写挂载脚本mount.sh并安装相关工具2.3、轻量级的桌面环境 lubuntu-desktop2.4、卸载一些不必要的软件2.5、添加用户2.6 、允许root用户登录桌面2.7、串口自动登录2.8、添加分区释放…...

本地新建项目如何推到码云上去
1.先在码云上建立一个空仓库,正常步骤就行。建立完成有readme.md. 2.然后本地建立项目文件,正常脚手架搭建VUE\REACT等。记得要项目git init一下。 3.本地改好的内容commit 一下。 4.本地文件与远端仓库建立连接。git remote add origin https://gite…...
加密解密)
RSAUtil 前端 JavaScript JSEncrypt 实现 RSA (长文本)加密解密
文章归档:https://www.yuque.com/u27599042/coding_star/cl4dl599pdmtllw1 依赖 import JSEncrypt from ‘jsencrypt’ pnpm i jsencryptimport {stringIsNull} from “/utils/string_utils.js”:https://www.yuque.com/u27599042/coding_star/slncupw…...
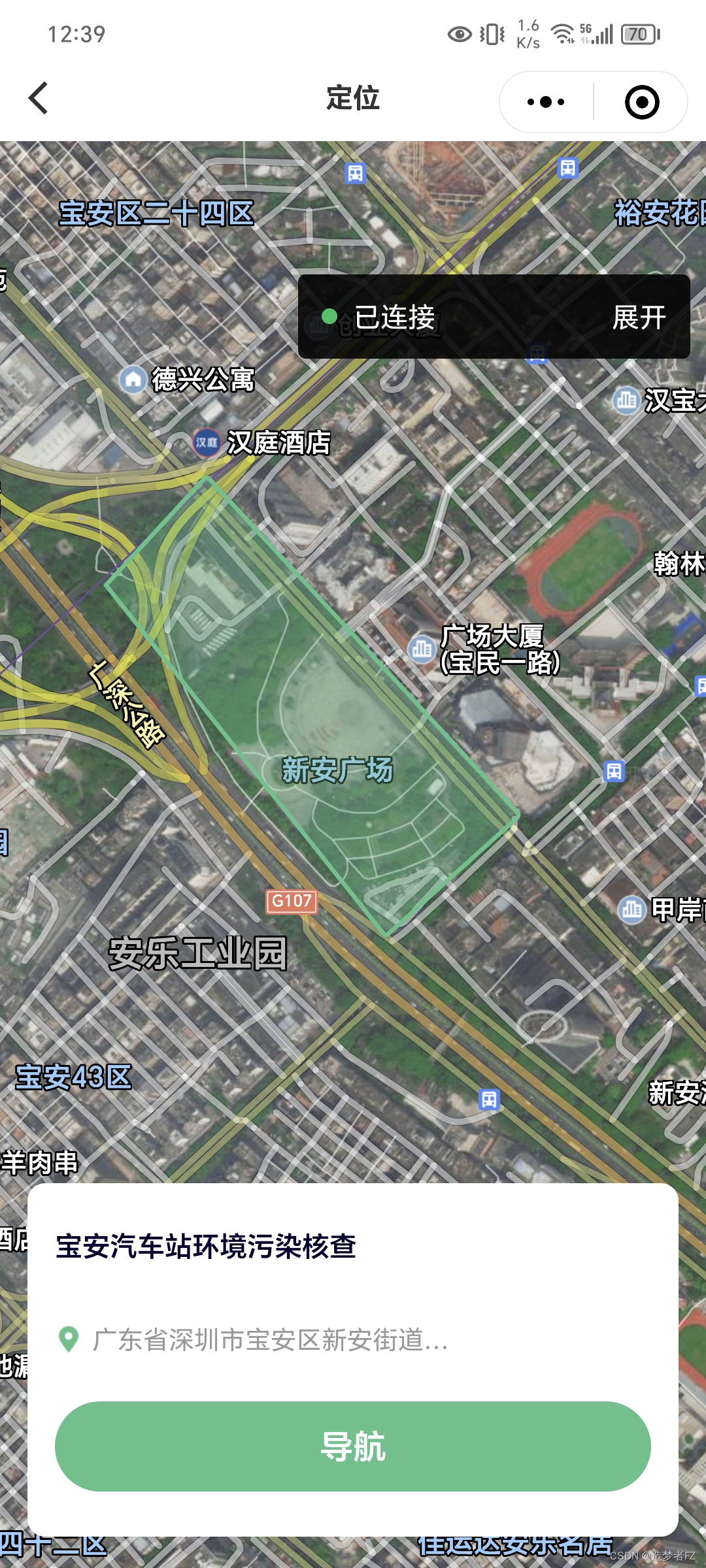
uniapp map polygons 区域填充色(fillColor)在ios显示正常,但在安卓手机显示是黑色的,怎么解决?
uniapp map polygons 区域填充色(fillColor)在ios显示正常,但在安卓手机显示是黑色的,怎么解决? <MapPage :longitude"item.centerCoord[0]" :latitude"item.centerCoord[1]":polygons"[{ points: it…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
