深度学习_5_模型拟合_梯度下降原理
需求:
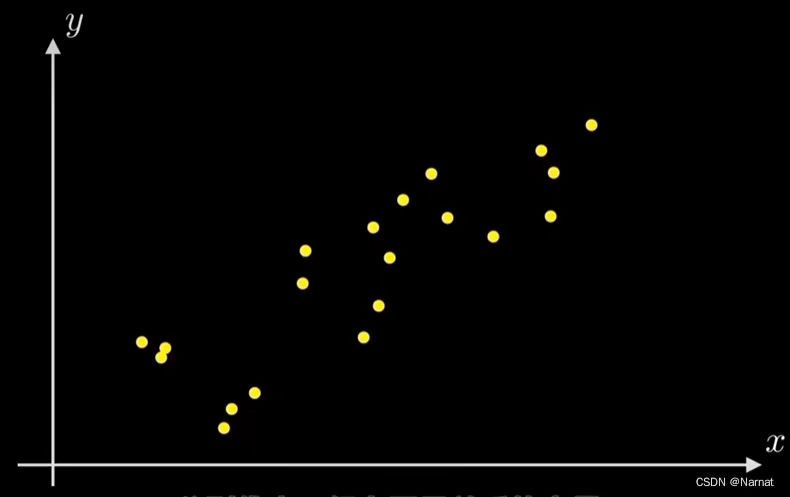
想要找到一条直线,能更好的拟合这一些点

如何确定上述直线就是最优解呢?
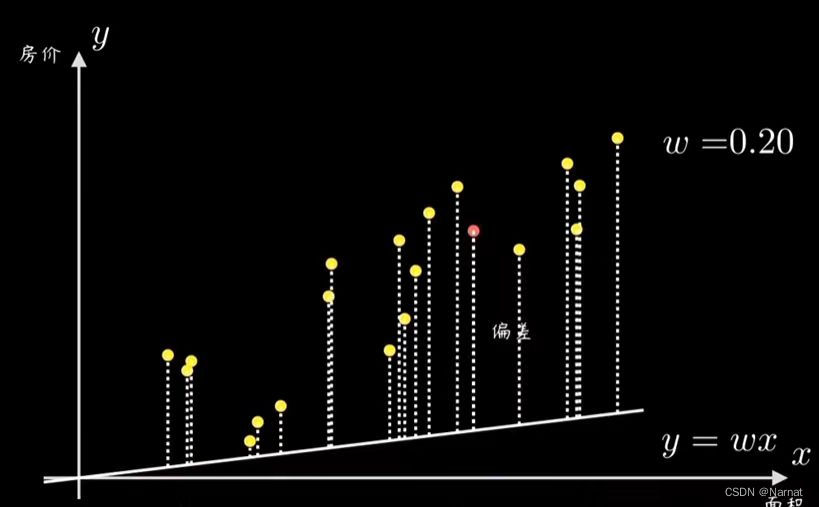
由计算机算出所有点与我们拟合直线的误差,常见的是均方误差
例如:P1与直线之间的误差为e1

将P1坐标带入直线并求误差得:
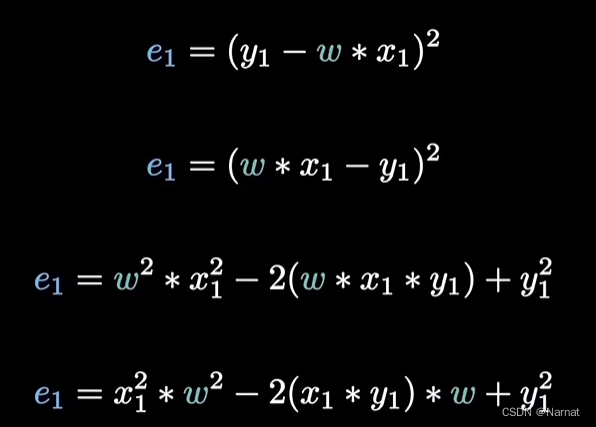
推广到所有点:
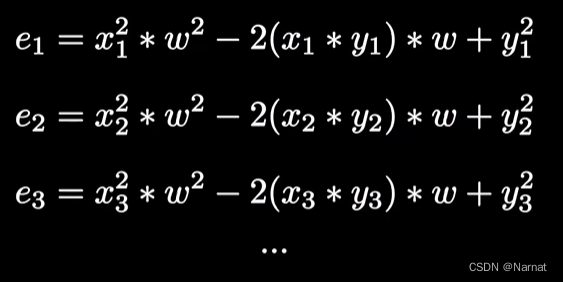
整合:
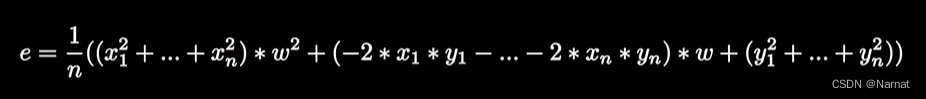
由于xi, yi都为已知点,那么它们就是常数
化简:
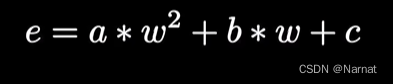
这个误差函数就称为代价函数,其中a, b, c为常数,w为直线得斜率
目标:
找到一个斜率w能使这条直线能更好得拟合上述所有点,反应出来的实质就是e最小
简而言之就是找到一个最优解w0使e最小
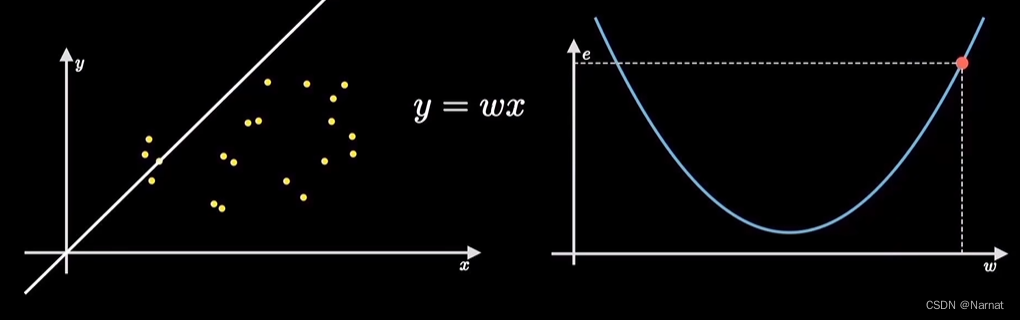
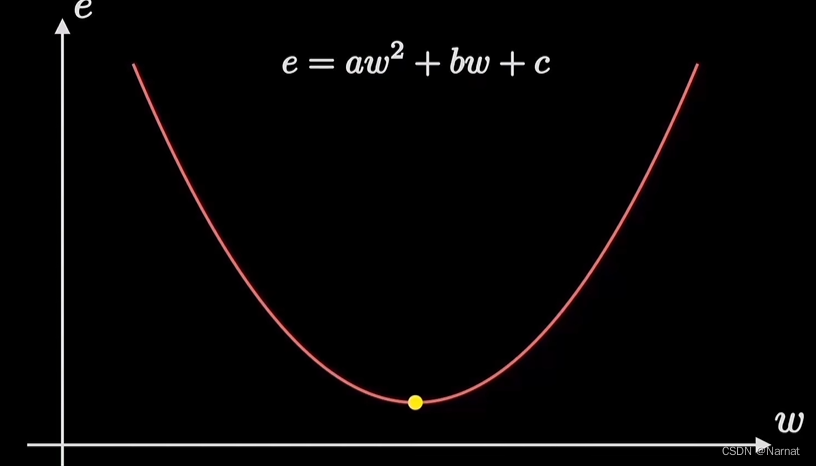
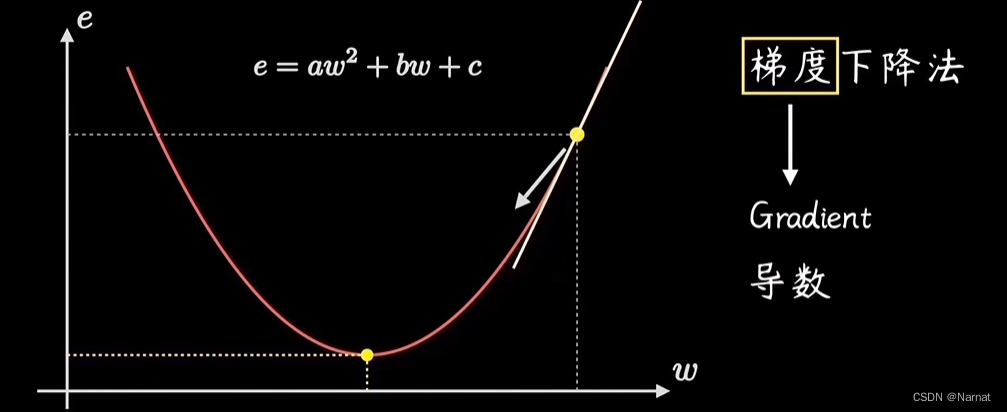
对于最优解w0,当w > w0时w位置所对应导数(也称斜率或梯度)大于零,w < w0时导数小于零
所以为了更好的迭代出最优解,得出以下迭代公式:

等高线大致可以这样理解:
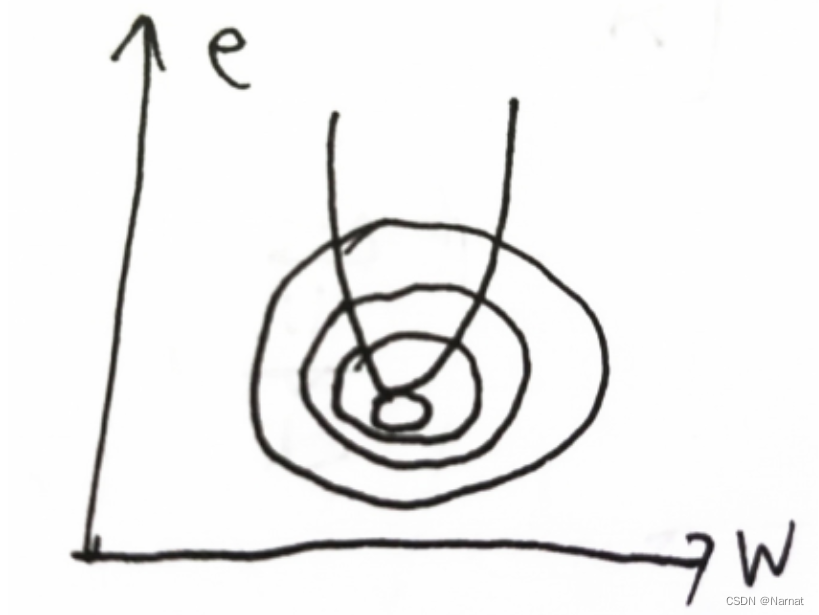
学习率过大过小都不行,太大了下降过快,太小了太慢
为什么不直接用 w = -b/2*a求解?
要拟合这些点,直线就得是y = k * x + b,这可有两个变量
按照上述理论求代价函数为了防止与常数向量表示重复,我用x = k, y = b
最后得到:
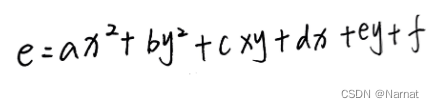
其中a,b,c,d,e,f均为常数
那么此方程就一个三维的了,x = -b/2a也不顶用了
求解过程:
使用梯度下降优化 k 和 b 的基本步骤:1.初始化 k 和 b 的值。2.定义损失函数,常见的选择是均方误差(Mean Squared Error)损失函数。
它可以表示为 loss = (1/N) * sum( (y - (kx + b))^2 ),其中 N 是点的数量,y 是真实的 y 值,x 是对应的 x 值。3.计算损失函数关于 k 和 b 的梯度。这可以通过计算损失函数对 k 和 b 的偏导数来实现。4.使用梯度下降算法更新 k 和 b。梯度下降的更新规则为 k = k - learning_rate * gradient_k,b = b - learning_rate * gradient_b,其中 learning_rate 是学习率,
gradient_k 和 gradient_b 是损失函数关于 k 和 b 的梯度。重复步骤 3 和 4,直到达到停止条件(例如达到一定的迭代次数或损失函数的变化小于某个阈值)。
计算机会不断得通过这个梯度下降的过程找到最优解x, y,这也就是为什么学习次数达到一定量构建出来的模型也更精确
疑惑:
1、为什么损失函数最小对应的损失函数对k的偏导与损失函数对应b的偏导值趋近于零?
当损失函数对模型参数的偏导数趋近于零时,意味着在该参数值附近,损失函数的变化非常小,再进行参数更新可能不会有明显的改进。这时,我们可以认为模型已经接近局部最优解,损失函数的值也趋近于最小值。
具体来说,对于线性回归模型中的参数 k 和 b,损失函数对 k 的偏导数和对 b
的偏导数的趋近于零表示在当前参数值附近,沿着每个参数的变化方向,损失函数的变化非常小。这可以解释为损失函数对参数的梯度几乎为零,即在该点附近的斜率几乎为零,导致参数不会有太大的变化。当参数的梯度趋近于零时,梯度下降算法会收敛,即停止参数更新,认为找到了局部最优解或者接近最优解。这是梯度下降算法的终止条件之一。但需要注意的是,梯度下降可能会停在局部最优解而非全局最优解,因此在实际应用中,可以通过调节学习率等参数来控制梯度下降的迭代过程,以更好地找到最优解。
2、什么是局部最优解和全局最优解?
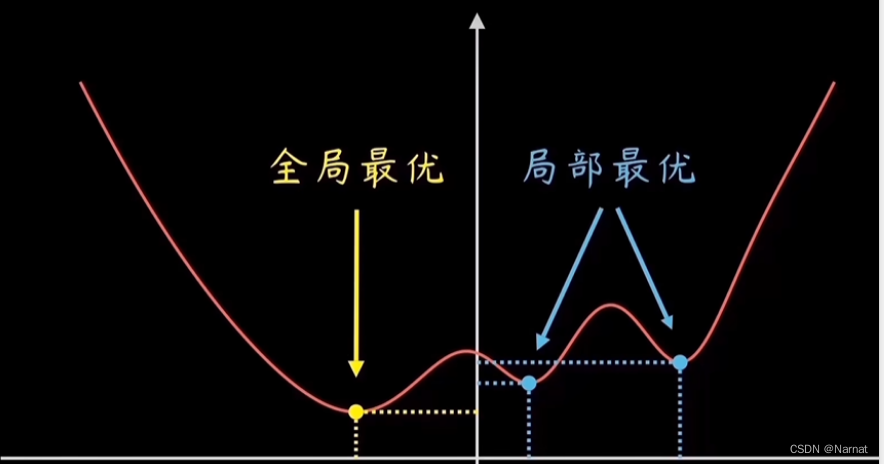
这也正是为什么利用机器学习产生的模型会产生大的误差
3、怎么能确保这个最小值e是全局最小而不是局部最小
为了确保找到的最小值是全局最小而不是局部最小,我们可以采用以下方法:
1、使用随机初始化参数的方法。通过多次运行算法并随机初始化参数,可以增加找到全局最小的概率。
2、调整学习率。如果学习率过大,可能会导致算法在最小值附近震荡而无法收敛到全局最小;如果学习率过小,则算法可能会陷入局部最小。因此,需要适当调整学习率的大小。
3、使用动量法或自适应学习率法等优化算法。这些算法可以在梯度变化缓慢时加速收敛,而在梯度变化剧烈时减小更新幅度,从而避免陷入局部最小。
4、添加正则化项。正则化项可以限制模型的复杂度,防止模型过度拟合训练数据,从而提高模型的泛化能力。同时,正则化项也可以使损失函数更加平滑,减少陷入局部最小的可能性。
学习渠道:梯度下降 & Chatgdp
相关文章:

深度学习_5_模型拟合_梯度下降原理
需求: 想要找到一条直线,能更好的拟合这一些点 如何确定上述直线就是最优解呢? 由计算机算出所有点与我们拟合直线的误差,常见的是均方误差 例如:P1与直线之间的误差为e1 将P1坐标带入直线并求误差得: 推广到所有点&a…...

大模型时代,AI如何成为数实融合的驱动力?
10月25日,百度APP、百家号联合中兴通讯举办的“时代的增量“主题沙龙第二期在北京顺利召开。本期沙龙围绕“数实融合新视角”邀请学界、业界、媒体从业者等领域专家出席,以产学研相结合的视角深入探讨数实融合的最新技术趋势,并围绕数实融合在…...

MS COCO数据集的评价标准以及不同指标的选择推荐(AP、mAP、MS COCO、AR、@、0.5、0.75、1、目标检测、评价指标)
目标检测模型性能衡量指标、MS COCO 数据集的评价标准以及不同指标的选择推荐 0. 引言 0.1 COCO 数据集评价指标 目标检测模型通过 pycocotools 在验证集上会得到 COCO 的评价列表,具体参数的含义是什么呢? 0.2 目标检测领域常用的公开数据集 PASCAL …...

css实现鼠标多样化
cursor pointer: 手型default: 箭头text: 文本输入光标move: …...
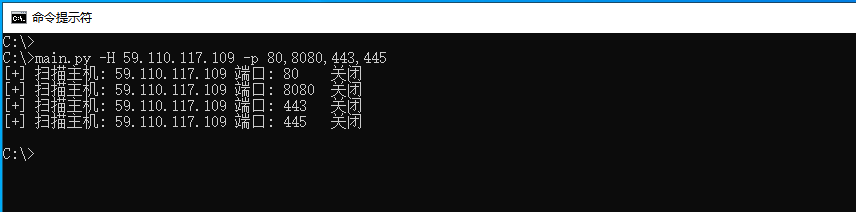
21.2 Python 使用Scapy实现端口探测
Scapy 是一款使用纯Python编写的跨平台网络数据包操控工具,它能够处理和嗅探各种网络数据包。能够很容易的创建,发送,捕获,分析和操作网络数据包,包括TCP,UDP,ICMP等协议,此外它还提…...
Qt设计一个自定义的登录框窗口
今天写了一个Qt登录、注册的小demo,后续完善会连接MySQL使用,过几天写完我会放在github上。 主要页面: 动态演示: 写完这个界面后,我终于知道了Qt为什么几乎没什么好看的窗口设计了,随便写一个简单大方的登…...
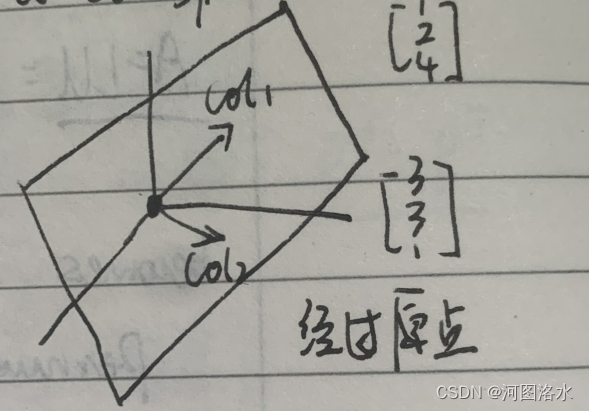
05 MIT线性代数-转置,置换,向量空间Transposes, permutations, spaces
1. Permutations P: execute row exchanges becomes PA LU for any invertible A Permutations P identity matrix with reordered rows mn (n-1) ... (3) (2) (1) counts recordings, counts all nxn permuations 对于nxn矩阵存在着n!个置换矩阵 , 2. Transpose: 2.…...
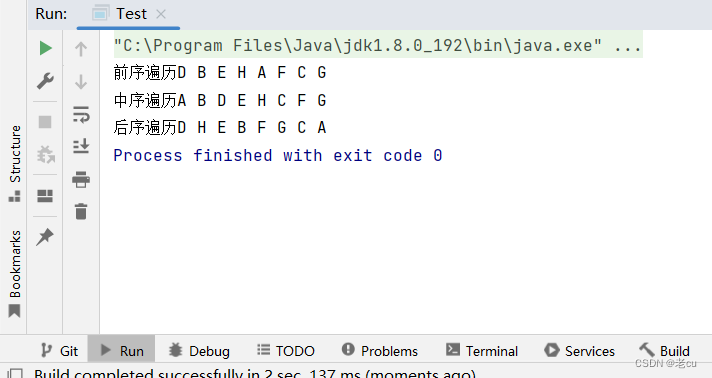
[数据结构】二叉树
1.概念 一棵二叉树是结点的一个有限集合,该集合: 1. 或者为空 2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成 从上图我们可以发现: 1.二叉树不存在大于2 的度 2.二叉树的子树有左右之分,次序不能颠倒。是有…...
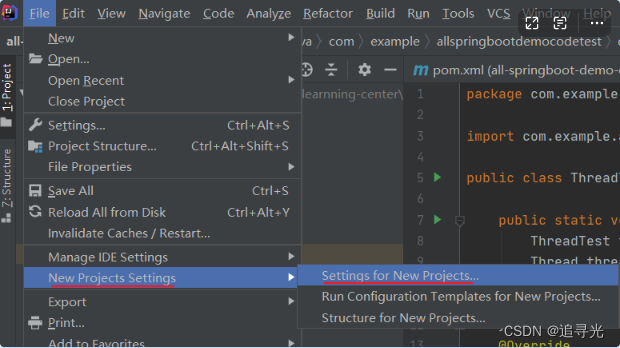
idea 中配置 maven
前文叙述: 配置 maven 一共要设置两个地方:1、为当前项目设置2、为新项目设置maven 的下载和安装可参考我之前写过的文章,具体的配置文章中也都有讲解。1、为当前项目进行 maven 配置 配置 VM Options: -DarchetypeCataloginternal2、为新项…...
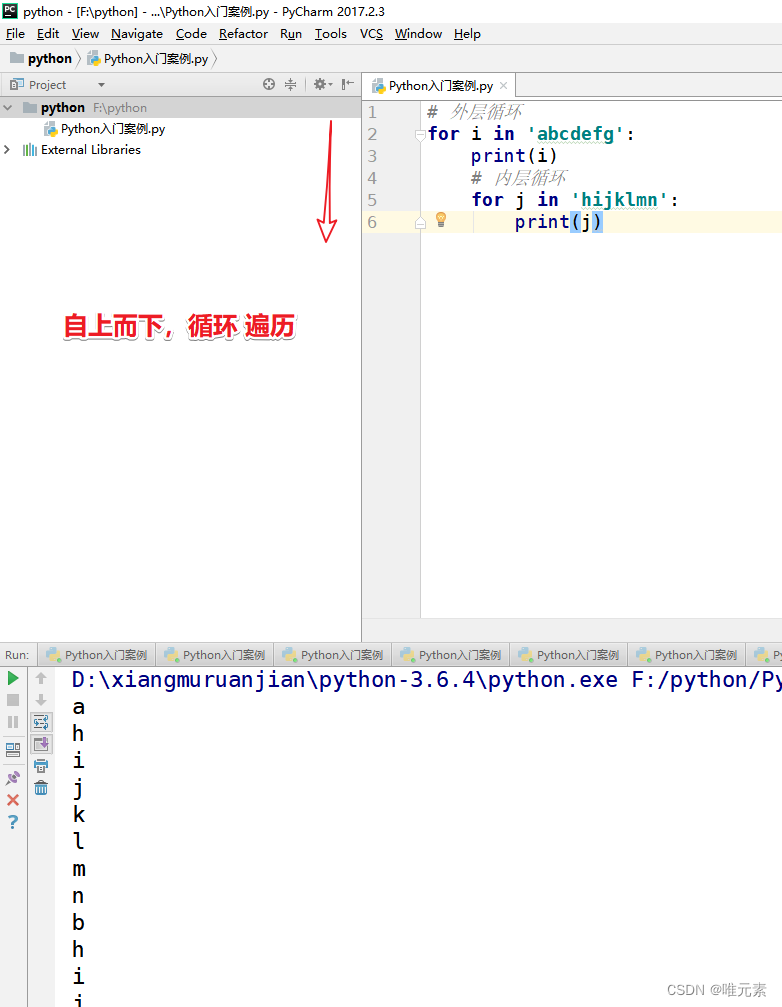
Python---for循环嵌套
for循环嵌套,就是一个for循环里面嵌套另外一个for循环的写法。 当循环结构相互嵌套时,位于外层的循环结构常简称为外层循环或外循环,位于内层的循环结构常简称为内层循环或内循环。 基本语法: # 外层循环 for i in 序列1:# 内层…...

189. 轮转数组 --力扣 --JAVA
题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 解题思路 通过位移后位置对数组长度的取余来判断元素变换后的位置 代码展示 class Solution {public void rotate(int[] nums, int k) {int size nums.length;int[]…...
C# 使用waveIn实现声音采集
文章目录 前言一、需要的对象及方法二、整体流程三、关键实现1、使用Thread开启线程2、TaskCompletionSource实现异步3、将指针封装为Stream 四、完整代码1.接口2.具体实现 五、使用示例方式一方式二 总结 前言 之前实现了《C 使用waveIn实现声音采集》,后来C#项目…...
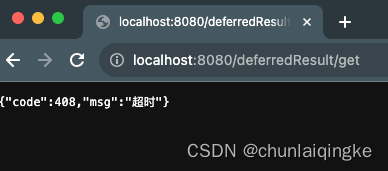
长连接的原理
Apollo的长连接实现是 Spring的DeferredResult来实现的,先看怎么用 import ...RestController RequestMapping("deferredResult") public class DeferredResultController {private Map<String, Consumer<DeferredResultResponse>> taskMap new HashMa…...

软考系列(系统架构师)- 2015年系统架构师软考案例分析考点
试题一 软件架构(质量属性效用树、架构风险、依够点、权衡点) 【问题1】(12分) 在架构评估过程中,质量属性效用树(utility tree)是对系统质量属性进行识别和优先级排序的重要工具。请给出合适的…...

小程序开发——小程序的视图与渲染
1.视图与渲染过程 基本概念: 视图层由WXML页面文件和样式文件WXSS共同组成。事件是视图层和逻辑层沟通的纽带,用户操作触发事件后可通过同名的事件处理函数执行相应的逻辑,处理完成后,更新的数据又将再次渲染到页面上。 WXML页面…...

用python实现操作mongodb的插入和查找操作
用python实现操作mongodb的插入和查找操作 import pymongoclient pymongo.MongoClient("mongo://localhost:27017") db client["app"] col db["C1"]# 插入一条数据 #user { # "name": "Sam", # "age":…...
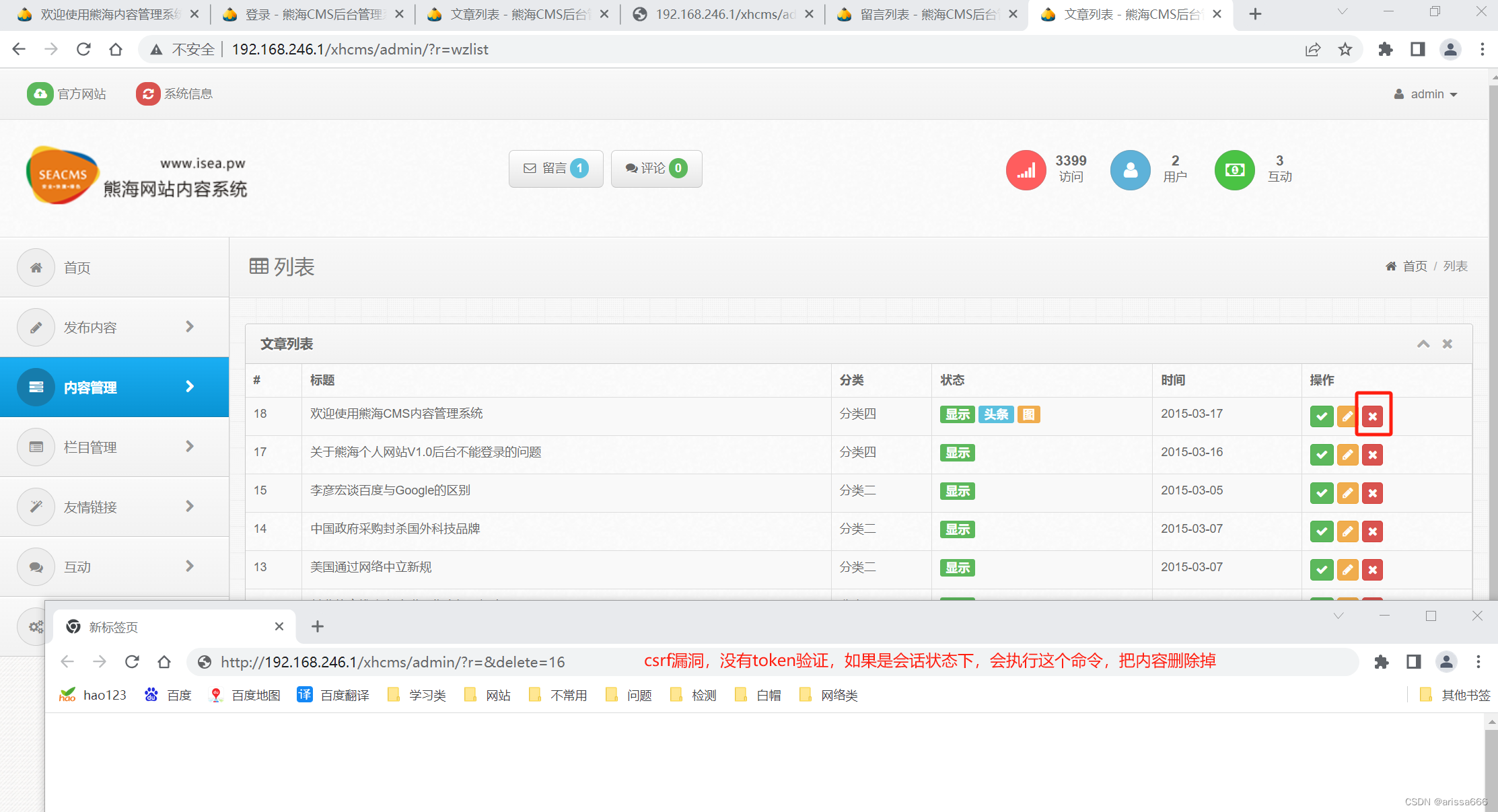
代码审计及示例
简介: 代码安全测试是从安全的角度对代码进行的安全测试评估。 结合丰富的安全知识、编程经验、测试技术,利用静态分析和人工审核的方法寻找代码在架构和编码上的安全缺陷,在代码形成软件产品前将业务软件的安全风险降到最低。 方法&#x…...

【Kotlin精简】第6章 反射
1 反射简介 反射机制是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法,对于任意一个对象,都能够调用它的任意一个方法和属性。 1.1 Kotlin反射 我们对比Kotlin和Java的反射类图。 1.1.1 Kotlin反射常用的数据结…...

基于FPGA的电风扇控制器verilog,视频/代码
名称:基于FPGA的电风扇控制器verilog 软件:QuartusII 语言:Verilog 代码功能: 基于FPGA的电风扇控制器 运用 EDA SOPO实验开发系统设计一个基于FPGA的电风扇定时开关控制器,能实现手动和自动模式之间的切换。要求: (1)KI为电…...

【MySQL】区分:等值连接/自连接/自然连接/外连接 以及ON和Where使用
区分:等值连接/自连接/自然连接/外连接 以及ON和Where使用 一、等值连接二、自连接三、自然连接四、外连接1.左外连接2.右外连接3.全外连接 五、using 和 on六、JOIN 关联表中 ON、WHERE 后面跟条件的区别 一、等值连接 等值连接:它是基于两个表之间的相…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
