[数据结构】二叉树
1.概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成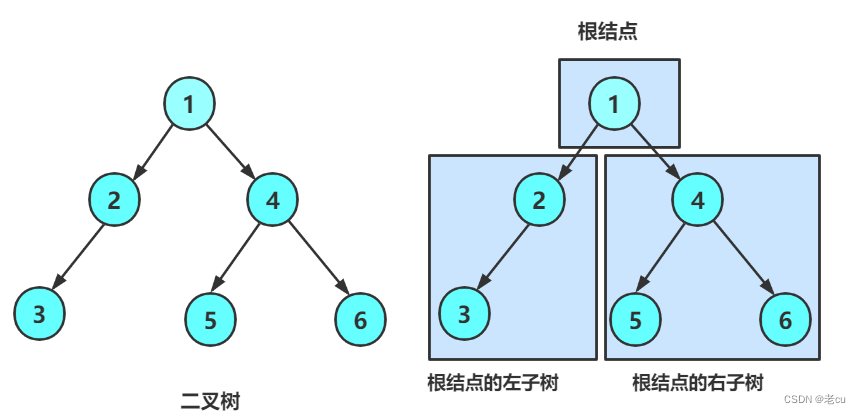
从上图我们可以发现:
1.二叉树不存在大于2 的度
2.二叉树的子树有左右之分,次序不能颠倒。是有序树
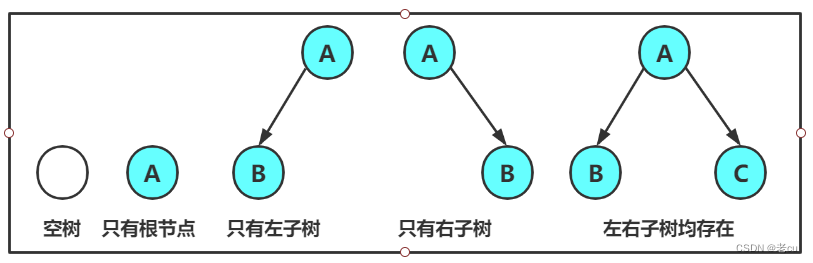
任意二叉树都是由上图构成的
2.两种特殊的二叉树
2.1.满二叉树
如果一棵二叉树每层的节点都达到最大值,则我们称这颗二叉树为满二叉树。
如果一棵二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。
2.2完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
3.二叉树的性质
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2^i-1(i>0)个结点
2. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k-1(k>=0)
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
4. 具有n个结点的完全二叉树的深度k为 log2(n+1)上取整
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i
的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
4.二叉树的存储
二叉树的存储分为:顺序存储和链式存储
我将在下一篇博客中给大家介绍顺序存储,我们先来看看链式存储:
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树} // 孩子双亲表示法class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点}5.二叉树的基本操作
为了方便大家理解,这里我先手动快速创建一颗二叉树:
·
static class TreeNode {public char val;public TreeNode left;public TreeNode right;TreeNode(char val) {this.val = val;}}public TreeNode create(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left=B;A.right=C;B.left=D;B.right=E;E.right=H;C.left=F;C.right=G;return A;}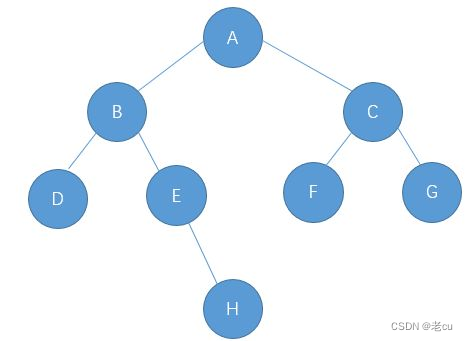 再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
5.1 二叉树的遍历
1. 前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点
// 前序遍历void preOrder(TreeNode root){if(root == null){return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);};// 中序遍历void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);};// 后序遍历void postOrder(TreeNode root){if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}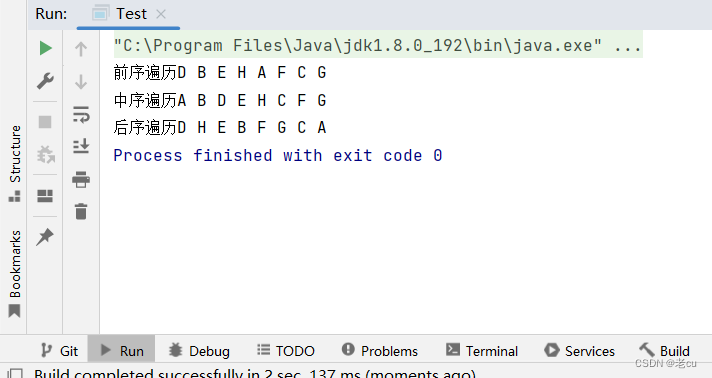 2. 层序遍历
2. 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层
上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
5. 二叉树的基本操作
public class BinaryTree {static class TreeNode {public char val;public TreeNode left;public TreeNode right;TreeNode(char val) {this.val = val;}}public TreeNode create(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');TreeNode g = new TreeNode('g');A.left=B;A.right=C;B.left=D;B.right=E;E.right=H;C.left=F;C.right=G;return A;}// 前序遍历void preOrder(TreeNode root){if(root == null){return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);};// 中序遍历void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);};// 后序遍历void postOrder(TreeNode root){if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}public int size;// 获取树中节点的个数int size(TreeNode root){if(root == null){return 0;}int leftSize = size(root.left);int rightSize = size(root.right);return leftSize+rightSize+1;}// 获取叶子节点的个数int getLeafNodeCount;int getLeafNodeCount(TreeNode root){if(root == null){return 0;}if(root.left == null && root.right ==null){return 1;}int leftSize =getLeafNodeCount(root.left);int rightSize=getLeafNodeCount(root.right);return leftSize+rightSize;}// 子问题思路-求叶子结点个数// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k){if(root == null ){return 0;}if(k == 1){return 1;}int leftSize = getKLevelNodeCount(root.left,k-1);int rightSize = getKLevelNodeCount(root.right,k-1);return leftSize+rightSize;}// 获取二叉树的高度int getHeight(TreeNode root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}int leftSize = getHeight(root.left);int rightSize = getHeight(root.right);return (Math.max(leftSize, rightSize)) +1 ;}// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val){if(root == null){return root;}if(root.val == val){return root;}TreeNode left = find(root.left,val);if(left !=null){return left;}TreeNode right = find(root.right,val);if(right != null){return right;}return null;}
}
相关文章:

[数据结构】二叉树
1.概念 一棵二叉树是结点的一个有限集合,该集合: 1. 或者为空 2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成 从上图我们可以发现: 1.二叉树不存在大于2 的度 2.二叉树的子树有左右之分,次序不能颠倒。是有…...
idea 中配置 maven
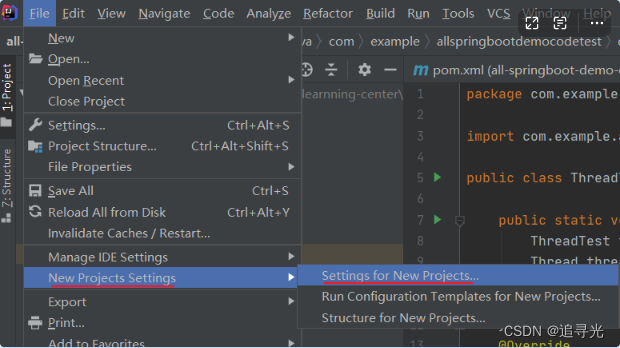
前文叙述: 配置 maven 一共要设置两个地方:1、为当前项目设置2、为新项目设置maven 的下载和安装可参考我之前写过的文章,具体的配置文章中也都有讲解。1、为当前项目进行 maven 配置 配置 VM Options: -DarchetypeCataloginternal2、为新项…...
Python---for循环嵌套
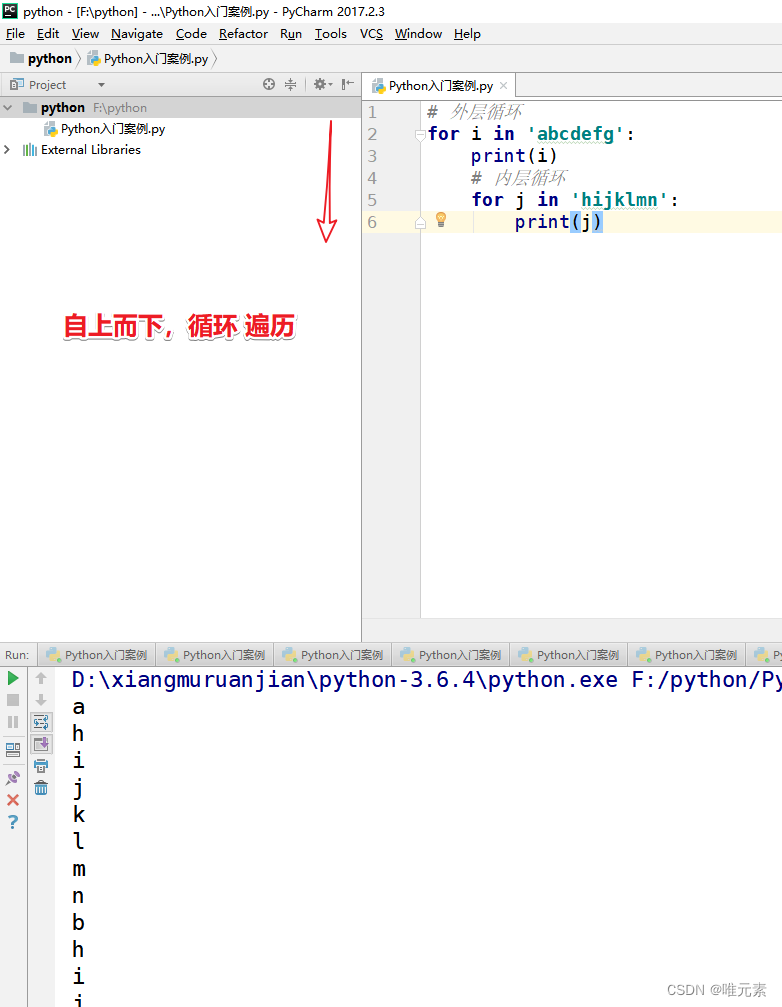
for循环嵌套,就是一个for循环里面嵌套另外一个for循环的写法。 当循环结构相互嵌套时,位于外层的循环结构常简称为外层循环或外循环,位于内层的循环结构常简称为内层循环或内循环。 基本语法: # 外层循环 for i in 序列1:# 内层…...

189. 轮转数组 --力扣 --JAVA
题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 解题思路 通过位移后位置对数组长度的取余来判断元素变换后的位置 代码展示 class Solution {public void rotate(int[] nums, int k) {int size nums.length;int[]…...
C# 使用waveIn实现声音采集
文章目录 前言一、需要的对象及方法二、整体流程三、关键实现1、使用Thread开启线程2、TaskCompletionSource实现异步3、将指针封装为Stream 四、完整代码1.接口2.具体实现 五、使用示例方式一方式二 总结 前言 之前实现了《C 使用waveIn实现声音采集》,后来C#项目…...
长连接的原理
Apollo的长连接实现是 Spring的DeferredResult来实现的,先看怎么用 import ...RestController RequestMapping("deferredResult") public class DeferredResultController {private Map<String, Consumer<DeferredResultResponse>> taskMap new HashMa…...

软考系列(系统架构师)- 2015年系统架构师软考案例分析考点
试题一 软件架构(质量属性效用树、架构风险、依够点、权衡点) 【问题1】(12分) 在架构评估过程中,质量属性效用树(utility tree)是对系统质量属性进行识别和优先级排序的重要工具。请给出合适的…...

小程序开发——小程序的视图与渲染
1.视图与渲染过程 基本概念: 视图层由WXML页面文件和样式文件WXSS共同组成。事件是视图层和逻辑层沟通的纽带,用户操作触发事件后可通过同名的事件处理函数执行相应的逻辑,处理完成后,更新的数据又将再次渲染到页面上。 WXML页面…...

用python实现操作mongodb的插入和查找操作
用python实现操作mongodb的插入和查找操作 import pymongoclient pymongo.MongoClient("mongo://localhost:27017") db client["app"] col db["C1"]# 插入一条数据 #user { # "name": "Sam", # "age":…...
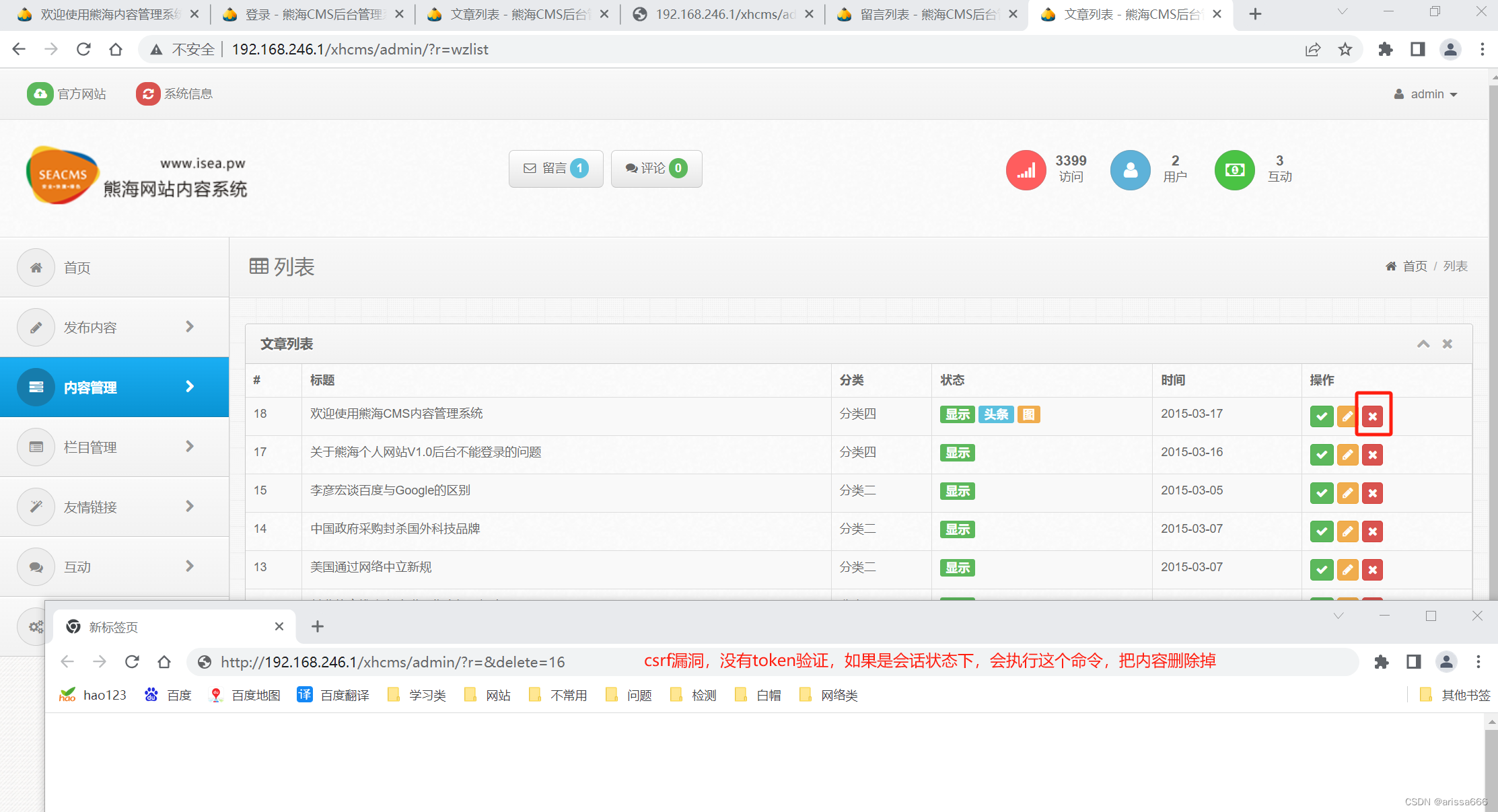
代码审计及示例
简介: 代码安全测试是从安全的角度对代码进行的安全测试评估。 结合丰富的安全知识、编程经验、测试技术,利用静态分析和人工审核的方法寻找代码在架构和编码上的安全缺陷,在代码形成软件产品前将业务软件的安全风险降到最低。 方法&#x…...

【Kotlin精简】第6章 反射
1 反射简介 反射机制是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法,对于任意一个对象,都能够调用它的任意一个方法和属性。 1.1 Kotlin反射 我们对比Kotlin和Java的反射类图。 1.1.1 Kotlin反射常用的数据结…...

基于FPGA的电风扇控制器verilog,视频/代码
名称:基于FPGA的电风扇控制器verilog 软件:QuartusII 语言:Verilog 代码功能: 基于FPGA的电风扇控制器 运用 EDA SOPO实验开发系统设计一个基于FPGA的电风扇定时开关控制器,能实现手动和自动模式之间的切换。要求: (1)KI为电…...

【MySQL】区分:等值连接/自连接/自然连接/外连接 以及ON和Where使用
区分:等值连接/自连接/自然连接/外连接 以及ON和Where使用 一、等值连接二、自连接三、自然连接四、外连接1.左外连接2.右外连接3.全外连接 五、using 和 on六、JOIN 关联表中 ON、WHERE 后面跟条件的区别 一、等值连接 等值连接:它是基于两个表之间的相…...
Windows环境下Apache安装部署说明及常见问题解决
一、软件准备 1.1 Python的下载与安装 见博客 链接: Python下载安装 1.2 Pycharm的下载与安装 见博客 链接: pycharm安装 1.3 Mysql的下载与安装 见博客 链接: MySQL安装 1.4 Navicat的下载与安装 可参考软件安装管家。 解释说明:Pycharm是Python的集成编译环境,Nav…...

Linux-安装docker-compose
前言:本文建立在服务器中已经存在docker环境的基础上,总结了安装docker-compose过程,以及安装过程中遇到的问题和解决方案。 一、下载docker-compose 在网上找了两种,一种是github官方的,一种是国内的镜像 gitbub官…...
机器学习实验一:KNN算法,手写数字数据集(使用汉明距离)
KNN-手写数字数据集: 使用sklearn中的KNN算法工具包( KNeighborsClassifier)替换实现分类器的构建,注意使用的是汉明距离; 分段解释代码: import os import pandas as pd from Levenshtein import hamming导入所需的库,包括os用于文件操作,pandas用于数据处理,以及hamm…...

Java零基础入门-赋值运算符
前言 Java是一门广泛被应用的编程语言,它被用于开发各种类型的应用程序,从桌面应用程序到企业级后端系统。对于零基础的人来说,学习Java可能会感到有些困难。本文将帮助那些没有编程经验的人了解Java的赋值运算符。 摘要 本文将介绍Java中…...
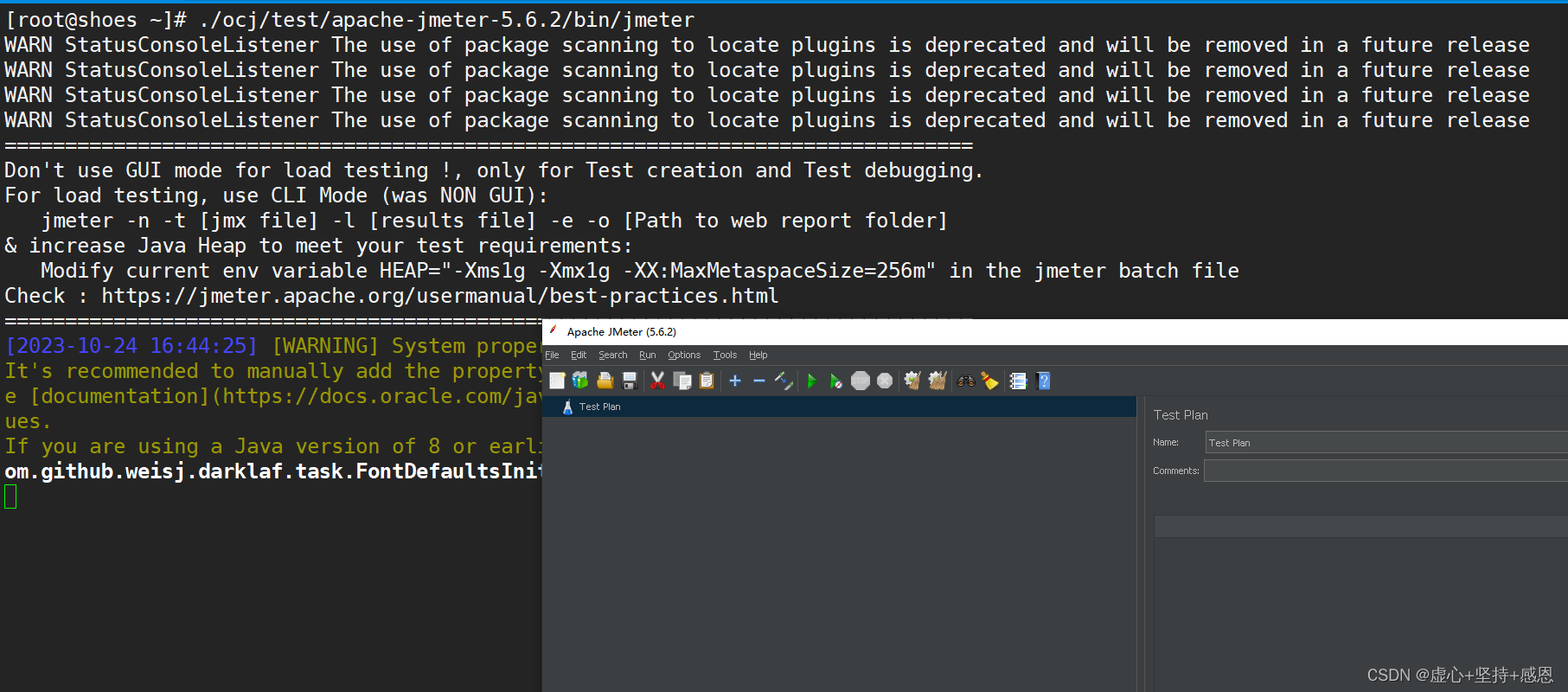
xshell+xming显示jmeter的gui页面
1.下载和安装xming,下载地址:https://sourceforge.net/projects/xming/ 2.配置xming 记住这个端口,一会要用到 修改进入xming安装目录修改host文件 此处是远程服务器的ip 3.服务器执行vi /etc/ssh/sshd_config,修改成如图所示…...

el-tree业务
<el-form-item label"选择节点" prop"node_ids"><el-checkboxv-if"regionList.length"v-model"selectAll":disabled"selectDisabled":indeterminate"isIndeterminate":show-checkbox"!selectDisabl…...

警惕Mallox勒索病毒的最新变种malloxx,您需要知道的预防和恢复方法。
导言: 恶意软件的威胁不断进化,其中之一是.malloxx勒索病毒。这种病毒可以加密您的文件,并要求您支付赎金以解锁它们。本文91数据恢复将详细介绍.malloxx勒索病毒,包括如何恢复被加密的数据文件以及如何预防这种威胁。如果受感染…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...
