06 MIT线性代数-列空间和零空间 Column space Nullspace
1. Vector space
Vector space requirements v+w and c v are in the space, all combs c v + d w are in the space
但是“子空间”和“子集”的概念有区别,所有元素都在原空间之内就可称之为子集,但是要满足对线性运算封闭的子集才能成为子空间
中 2 subspaces

L: line is a subspace
P: Plane through [0,0,0]T is a subspace of
= all vectors in P or L or both is not a subspace
= all vectors in both P and L is a subspace - null space
2. 列空间 Column space
column space of A is subspace of is C(A)=all linear combs. of columns

Does Ax=b have a solution for every b? No
cuz 4 equations and 3 unknowns 列向量的线性组合无法充满
which b's allow this system to be solved?
Can solve Ax=b exactly when b is in C(A) IN
由于列向量不是线性无关的,第三个列向量为前两个列向量之和,所以尽管有3个列向量,但是只有2个对张成向量空间有贡献。矩阵A的列空间为内的一个二维子空间
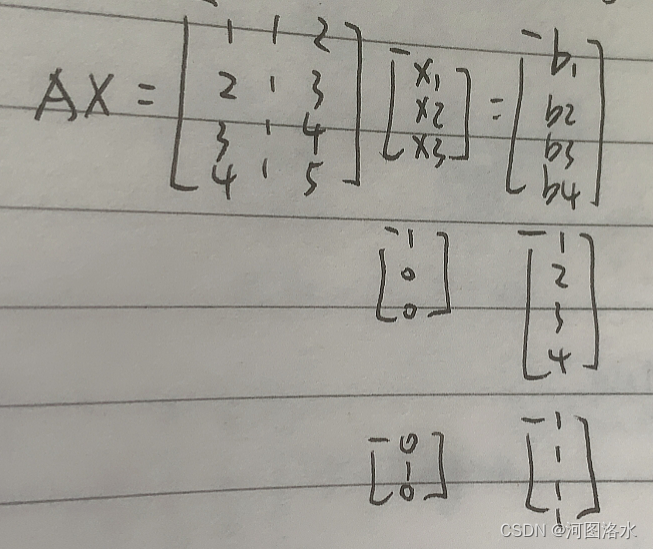
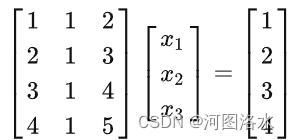
3.零空间(或化零空间)Nullspace
Null space of A = all solutions x = in
to Ax=0
对于所给定这个矩阵A,其列向量含有4个分量,因此列空间是空间的子空间。
x为含有3个分量的向量,故矩阵A的零空间是的子空间。对于mxn矩阵,列空间为
的子空间,零空间为
空间的子空间。
N(A) contains which is a line in
check that - solution to Ax=0 always give a subspace
if Av=0 and Aw = 0 then A(v+w)=0
then A(12v)=0
4. influence of b

subspaces have to go through the origin
5. summary:
2种构筑子空间方法
1.对于列空间,它是由列向量进行线性组合张成的空间
2.零空间是从方程组出发,通过让x满足特定条件而得到的子空间
相关文章:

06 MIT线性代数-列空间和零空间 Column space Nullspace
1. Vector space Vector space requirements vw and c v are in the space, all combs c v d w are in the space 但是“子空间”和“子集”的概念有区别,所有元素都在原空间之内就可称之为子集,但是要满足对线性运算封闭的子集才能成为子空间 中 2 …...

【每日一题Day360】LC1465切割后面积最大的蛋糕 | 贪心
切割后面积最大的蛋糕【LC1465】 矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCuts 和 verticalCuts,其中: horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口…...
中国地名信息库
地名是社会基本公共信息,是历史文化的重要载体。 2014年至2018年,国家启动实施并完成了第二次全国地名普查工作,全国共计采集地名1320多万条,修测标绘地名图2.4万多幅,新设更新地名标志68万多块,普遍建立了…...

网络时代下的声音之路:如何在中央新闻媒体发布网评稿
在当今数字时代,信息传播已经变得更加便捷和广泛。各大中央新闻媒体平台为民众提供了一个发布观点、表达意见的平台。在这个背景下,撰写并发布网评稿成为了一种重要的社会参与方式。根据媒介易软文发稿平台的总结,下面是探讨如何在各大中央新…...
Selenium中WebDriver最新Chrome驱动安装教程
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...
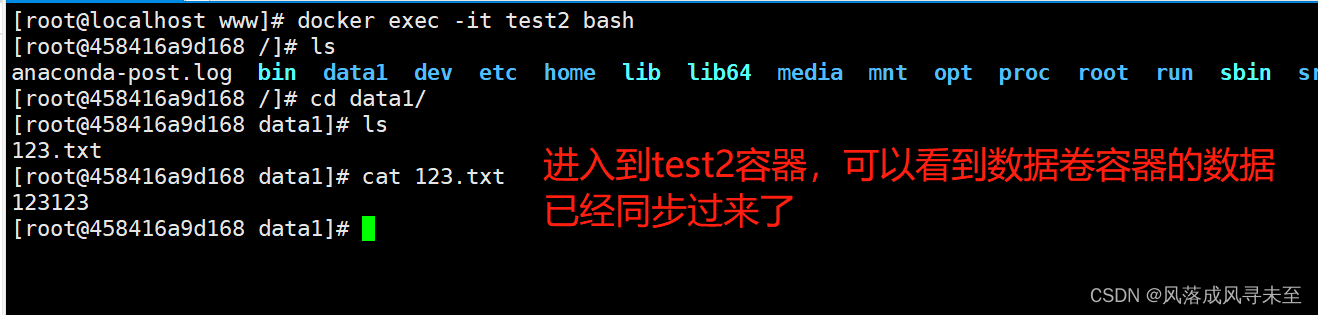
云原生Docker数据管理
目录 Docker的数据管理 数据卷 数据卷容器 容器互联 容器中管理数据主要有两种方式: 数据卷(Data Volumes)数据卷容器(Data Volume Dontainers) Docker的数据管理 数据卷 数据卷是一个供容器使用的特殊目录&a…...
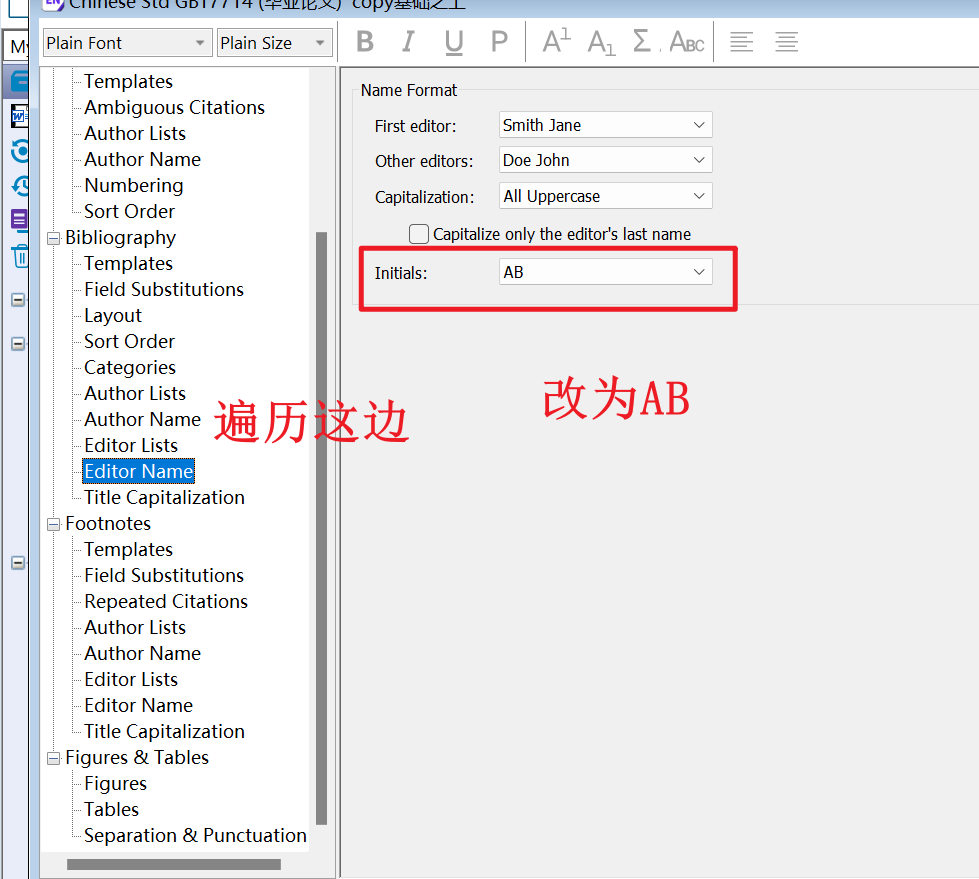
endnote设置
问题1:参考文献的tab太长 首先要在endnote里面这样设置,file->output->edit "XXX" 保存之后,在word更新目录。 在word里面设置悬挂缩进 结果: Endnote参考编号与参考文献距离太远怎么调整 endnote 文献对齐方式…...

计算机网络整理-简称缩写【期末复习|考研复习】
文章目录 前言一、物理层1.1 FDM频分复用 Frequency-division multiplexing1.2 TDM时分复用 Time-division multiplexing1.3 WDM波分复用 Wavelength Division Multiplexing1.4 Hub 集线器1.5 FSK频移键控 Frequency-shift keying 二、数据链路层2.1 GBN回退N步协议 Go Back N …...

Flink Hive Catalog操作案例
在此对Flink读写Hive表操作进行逐步记录,需要指出的是,其中操作Hive分区表和非分区表的DDL有所不同,以下分别记录。 基础环境 Hive-3.1.3 Flink-1.17.1 基本操作与准备 1、上传依赖jar包到flink/lib目录下 cp flink-sql-connector-hive-…...
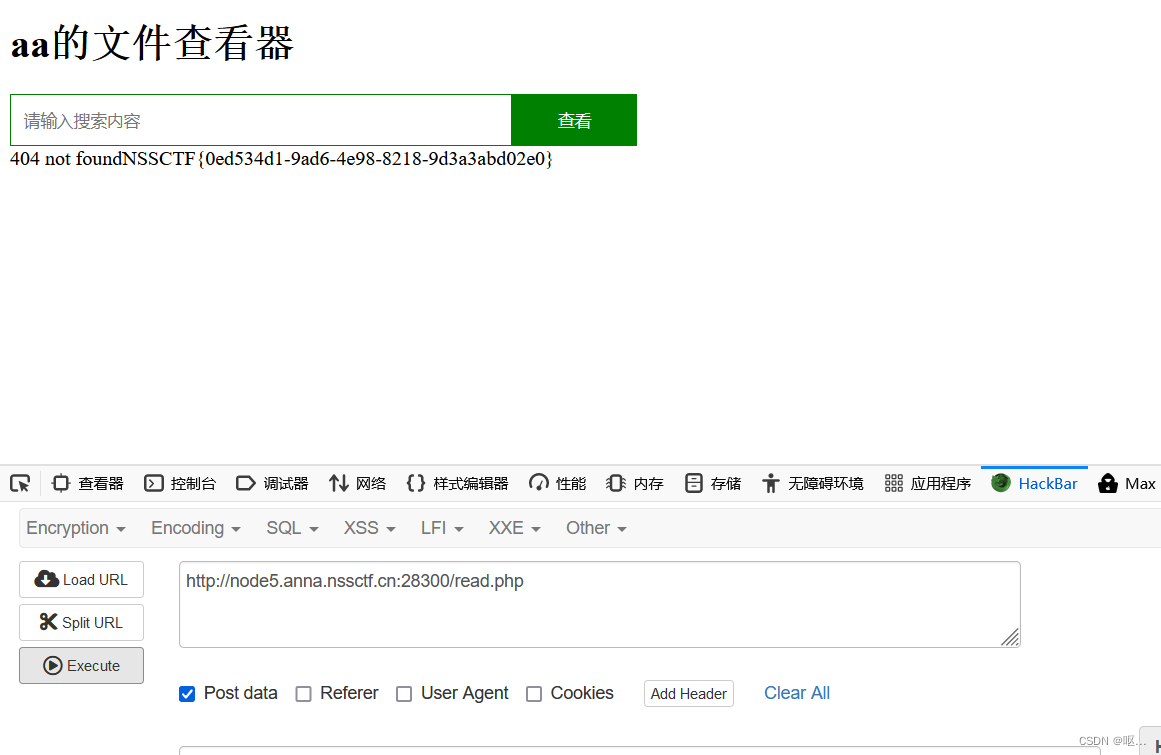
NSSCTF做题第9页(3)
[GKCTF 2020]CheckIN 代码审计 这段代码定义了一个名为ClassName的类,并在脚本的最后创建了一个ClassName类的实例。 在ClassName类的构造函数中,首先通过调用$this->x()方法获取了请求参数$_REQUEST中的值,并将其赋值给$this->code属性…...

从瀑布模式到水母模式:ChatGPT如何赋能软件研发全流程【文末送书五本】
从瀑布模式到水母模式:ChatGPT如何赋能软件研发全流程 前言内容简介购买链接作者简介专家推荐读者对象参与方式往期赠书回 🏘️🏘️个人简介:以山河作礼。 🎖️🎖️:Python领域新星创作者,CSDN实…...
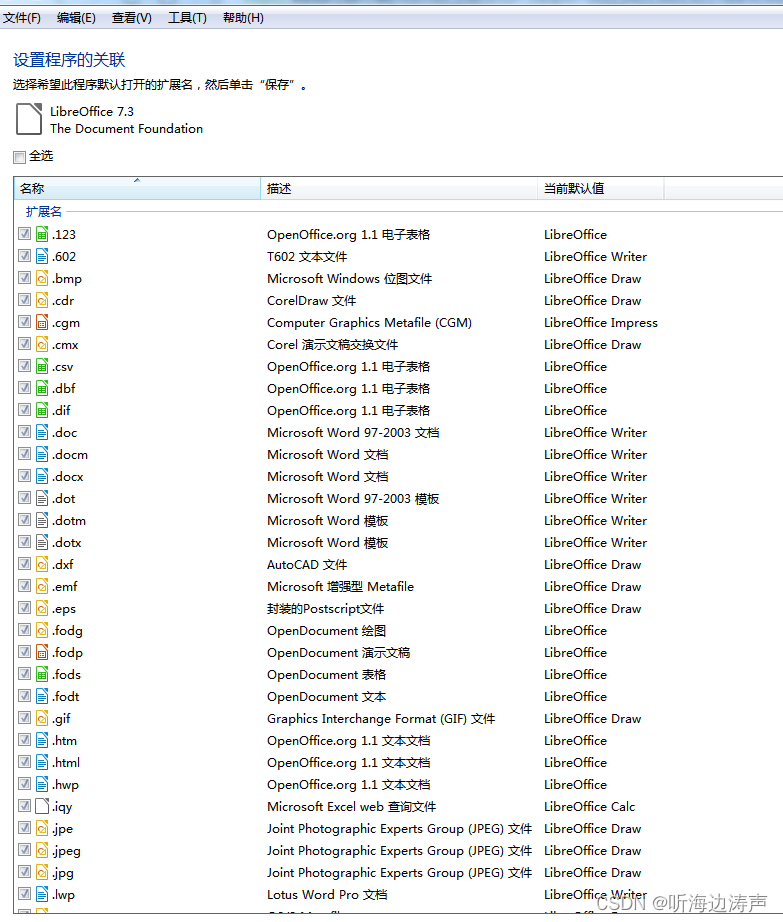
设置使用LibreOffice作为默认程序打开word、excel等文档
以win7为例。打开控制面板,点击程序: 点击“设置默认程序”: 左侧选中LibreOffice,然后在右下方点击“选择此程序的默认值”: 然后根据自己的需要勾选就行了:...

创新领航 | 竹云参编《基于区块链的数据资产评估实施指南》正式发布!
10月25日,由深圳数宝数据服务股份有限公司和深圳职业技术大学提出,中国科学院深圳先进技术研究院、中国电子技术标准化研究院、中国(天津)自由贸易试验区政策与产业创新发展局、网络空间治理与数字经济法治(长三角&…...
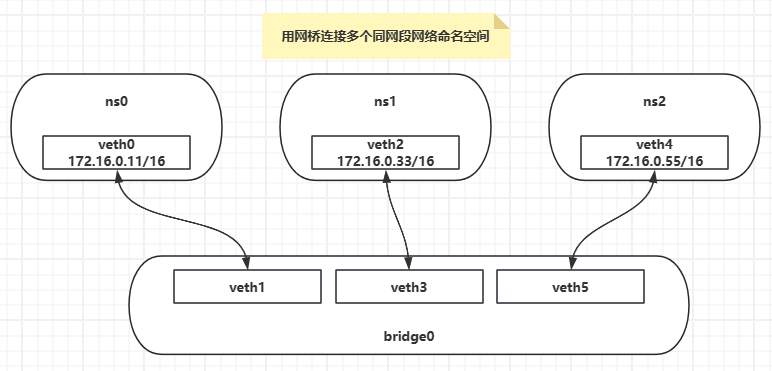
【Docker】Linux网桥连接多个命名空间
veth实现了点对点的虚拟连接,可以通过veth连接两个namespace,如果我们需要将3个或者多个namespace接入同一个二层网络时,就不能只使用veth了。 在物理网络中,如果需要连接多个主机,我们会使用bridge(网桥&…...

ES6新特性:let关键字详解
文章目录 1 声明提升2 作用域3 重复声明 在JavaScript中,let 和 var 都是声明变量的关键字,但在用法和作用域方面有一些区别。 let 是ES6引入的新的声明变量的关键字,它与 var 相比,更加严格,语法更加规范,…...
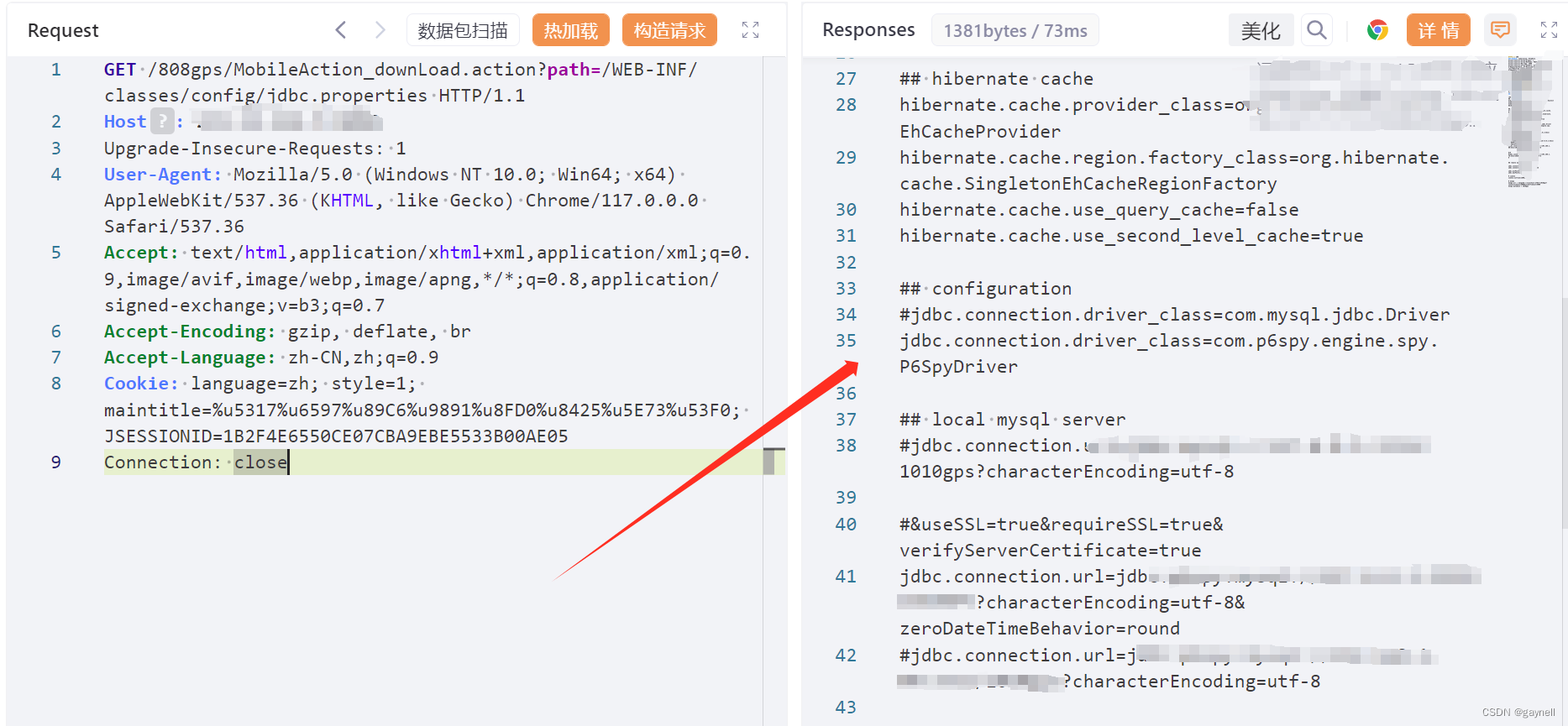
鸿运主动安全监控云平台任意文件下载漏洞复现 [附POC]
文章目录 鸿运主动安全监控云平台任意文件下载漏洞复现 [附POC]0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 鸿运主动安全监控云平台任意文件下载漏洞复现 [附POC] 0x01 前言 免责声明:请勿利用文章内的相关技术…...
使用pycharm远程连接到Linux服务器进行开发
预计达到的效果 本地的 PyCharm 能达到和远程服务器之间的文件同步;本地的 PyCharm 能够使用远程服务器的开发环境; 环境配置 PyCharm:PyCharm 2021.3 (Professional Edition)Linux服务器:Ubuntu20.04 步骤 1.进入配置项 配…...

JavaScript 中 BOM 基础知识有哪些?
浏览器对象模型(Browser Object Model,简称 BOM)是 JavaScript 的组成部分之一,BOM 赋予了 JavaScript 程序与浏览器交互的能力。 window 对象是 BOM 的核心,用来表示当前浏览器窗口,其中提供了一系列用来…...
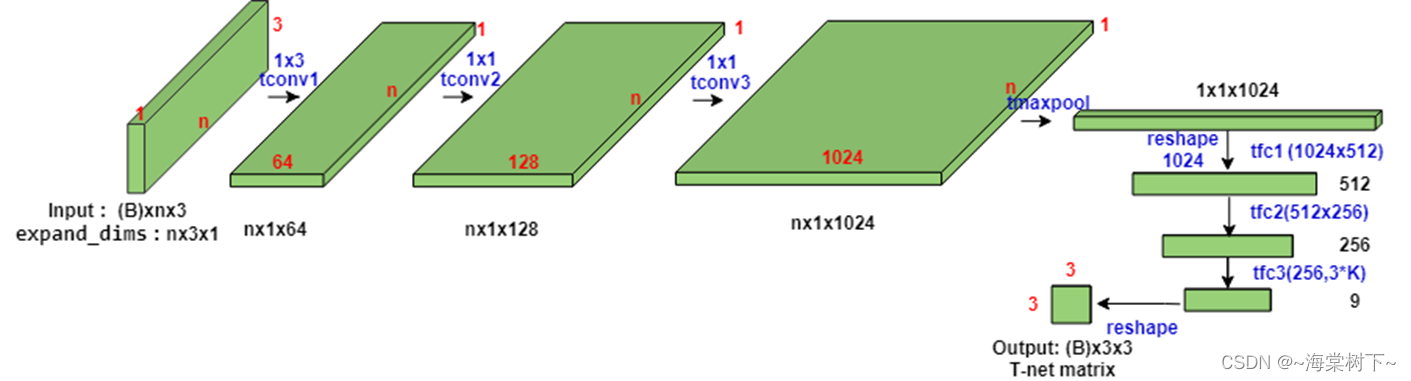
【PointNet—论文笔记分享】
第一个直接基于原始点云数据进行分割、分类的模型,之前都是基于多视图或者体素的方式。 论文: PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation代码: TensorFlow版 Pytorch版 基本模型架构: 分别对每个点进行特征提取…...
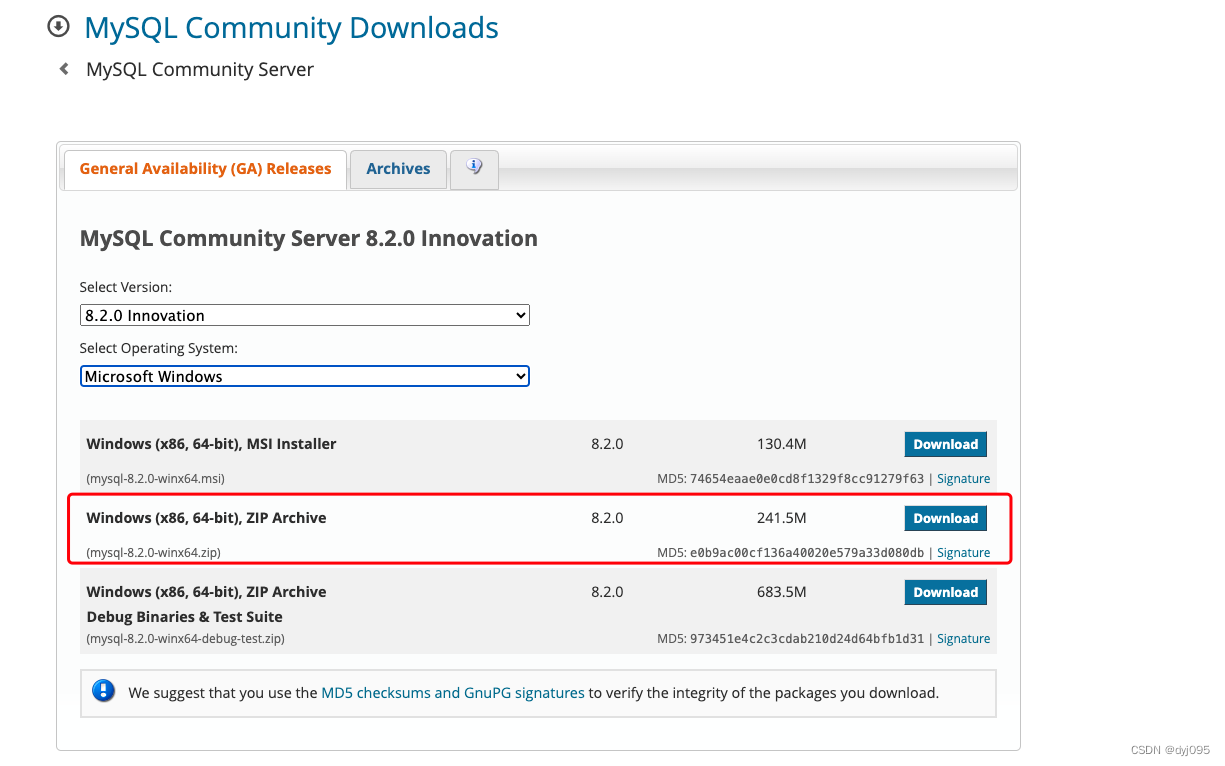
Mysql8.1.0 windows 绿色版安装
Mysql8.1.0 windows 绿色版安装 目录 Mysql8.1.0 windows 绿色版安装1、下载mysql8.1.0_windows(mysql-8.1.0-winx64.zip)2、解压到安装目录3、添加环境变量4、新建mysql配置文件5、安装mysql服务6、初始化数据文件7、启动mysql服务8、进入mysql管理模式…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
