14、KL散度
KL 散度,是一个用来衡量两个概率分布的相似性的一个度量指标。
现实世界里的任何观察都可以看成表示成信息和数据,一般来说,我们无法获取数据的总体,我们只能拿到数据的部分样本,根据数据的部分样本,我们会对数据的整体做一个近似的估计,而数据整体本身有一个真实的分布(我们可能永远无法知道)。
那么近似估计的概率分布和数据整体真实的概率分布的相似度,或者说差异程度,可以用 KL 散度来表示。
KL 散度,最早是从信息论里演化而来的。所以在介绍 KL 散度之前,先介绍一下信息论里有关熵的概念。
熵
信息论中,某个信息 xi\large x_{i}xi 出现的不确定性的大小定义为 xi\large x_{i}xi 所携带的信息量,用 I(xi)I(x_{i})I(xi) 表示。I(xi)I(x_{i})I(xi) 与信息 xi\large x_{i}xi 出现的概率 P(xi)P(x_{i})P(xi) 之间的关系为
I(xi)=log1P(xi)=−logP(xi)(1)\begin{aligned} I(x_i) = & log\frac{1}{P(x_i)} = -logP(x_i) \tag{1} \\ \end{aligned} I(xi)=logP(xi)1=−logP(xi)(1)
例:掷两枚骰子,求点数和为7的信息量 点数和为7的情况为:(1,6) ; (6,1) ; (2,5) ; (5,2) ; (3,4) ; (4,3) 这6种。总的情况为 6*6 = 36 种。
那么该信息出现的概率为 Px=7=636=16P_{x=7}=\frac{6}{36}=\frac{1}{6}Px=7=366=61
包含的信息量为 I(7)=−logP(7)=−log16=log6I(7)=-\log P(7)=-\log\frac{1}{6}=\log 6I(7)=−logP(7)=−log61=log6
以上是求单一信息的信息量。但实际情况中,会要求我们求多个信息的信息量,也就是平均信息量。
假设一共有 n 种信息,每种信息出现的概率情况由以下列出:
| X1X_1X1 | X2X_2X2 | X3X_3X3 | X4X_4X4 | ............... | XnX_nXn |
|---|---|---|---|---|---|
| P(x1)P(x_1)P(x1) | P(x2)P(x_2)P(x2) | P(x3)P(x_3)P(x3) | P(x4)P(x_4)P(x4) | … | P(xn)P(x_n)P(xn) |
同时满足:
∑i=1nP(xi)=1(2)\begin{aligned} \sum^n_{i=1} P(x_i) = 1 \tag{2} \\ \end{aligned} i=1∑nP(xi)=1(2)
则 x1,x2,.....,xnx_1,x_2,.....,x_nx1,x2,.....,xn 所包含的信息量分别是 KaTeX parse error: Undefined control sequence: \logP at position 2: -\̲l̲o̲g̲P̲(x_1),-\logP(x_…平均信息量为
KaTeX parse error: Undefined control sequence: \logP at position 49: …^n_{i=1} P(x_i)\̲l̲o̲g̲P̲(x_i) \tag{3} \…
H 与热力学中的熵的定义类似,故这又被称为信息熵。
与热力学中的熵的定义类似,故这又被称为信息熵。
H(x)=−(18log(18)+18log(18)+14log(14)+12log(12))=1.75\begin{aligned}H(x) = -(\frac{1}{8}\log(\frac{1}{8}) + \frac{1}{8}\log(\frac{1}{8}) + \frac{1}{4}\log(\frac{1}{4}) + \frac{1}{2}\log(\frac{1}{2}) ) = 1.75 \end{aligned}H(x)=−(81log(81)+81log(81)+41log(41)+21log(21))=1.75
连续信息的平均信息量可定义为
H(x)=−∫f(x)logf(x)dx(3)\begin{aligned} H(x) = -\int f(x)\log f(x)dx \tag{3} \end{aligned} H(x)=−∫f(x)logf(x)dx(3)
这里的 f(x)f(x)f(x) 是信息的概率密度。
上述我们提到了信息论中的信息熵
H(x)=−∑i=1nP(xi)logP(xi)=∑i=1nP(xi)log1P(xi)=H(P)(4)\begin{aligned} H(x) = -\sum^n_{i=1}P(x_i) \log P(x_i) = \sum^n_{i=1} P(x_i) \log \frac{1}{P(x_i)} = H(P) \tag{4} \end{aligned} H(x)=−i=1∑nP(xi)logP(xi)=i=1∑nP(xi)logP(xi)1=H(P)(4)
这是一个平均信息量,又可以解释为:用基于P的编码去编码来自P的样本,其最优编码平均所需要的比特个数
接下来我们再提一个概念:交叉熵
H(P,Q)=−∑i=1nP(xi)logQ(xi)=∑i=1nP(xi)log1Q(xi)(6)\begin{aligned} H(P,Q) = -\sum^n_{i=1}P(x_i) \log Q(x_i) = \sum^n_{i=1} P(x_i) \log \frac{1}{Q(x_i)} \tag{6} \end{aligned} H(P,Q)=−i=1∑nP(xi)logQ(xi)=i=1∑nP(xi)logQ(xi)1(6)
这就解释为:用基于P的编码去编码来自Q的样本,所需要的比特个数
【注】P(x)P(x)P(x) 为各字符出现的频率,log1P(x)\log \frac{1}{P(x)}logP(x)1 为该字符相应的编码长度,log1Q(x)\log \frac{1}{Q(x)}logQ(x)1 为对应于Q 的分布各字符编码长度。
KL 散度
让我们从一个问题开始我们的探索。假设我们是太空科学家,正在访问一个遥远的新行星,我们发现了一种咬人的蠕虫,我们想研究它。我们发现这些蠕虫有10颗牙齿,但由于它们不停地咀嚼,很多最后都掉了牙。在收集了许多样本后,我们得出了每条蠕虫牙齿数量的经验概率分布:
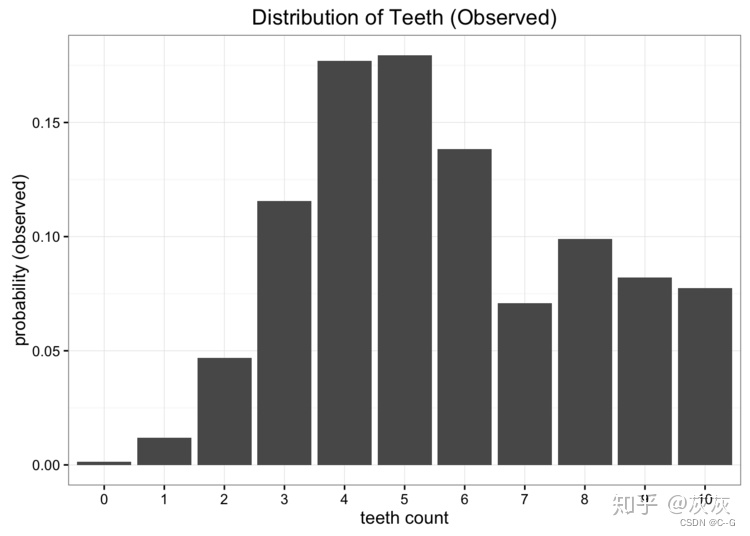
虽然这些数据很好,但我们有一个小问题。我们离地球很远,把数据寄回家很贵。我们要做的是将这些数据简化为一个只有一两个参数的简单模型。一种选择是将蠕虫牙齿的分布表示为均匀分布。我们知道有11个可能的值,我们可以指定1/11的均匀概率
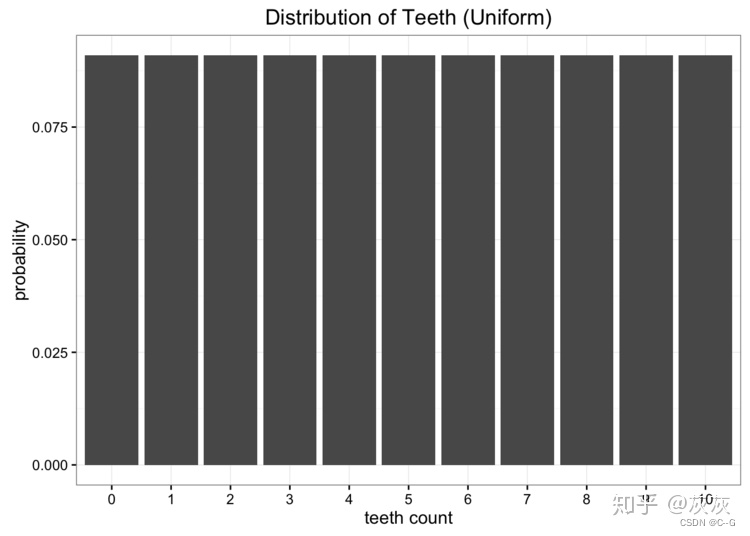
显然,我们的数据不是均匀分布的,但是看起来也不像我们所知道的任何常见分布。我们可以尝试的另一种选择是使用二项分布对数据进行建模。在这种情况下,我们要做的就是估计二项分布的概率参数。我们知道如果我们有n次试验,概率是p,那么期望就是E[x]= np。在本例中n = 10,期望值是我们数据的平均值,计算得到5.7,因此我们对p的最佳估计为0.57。这将使我们得到一个二项分布,如下所示:
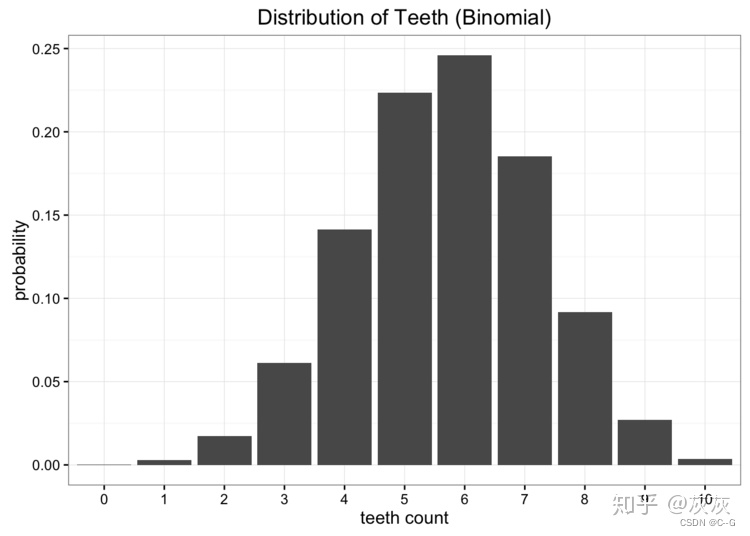
将我们的两个模型与原始数据进行比较,我们可以看出,两个都没有完美匹配原始分布,但是哪个更好?
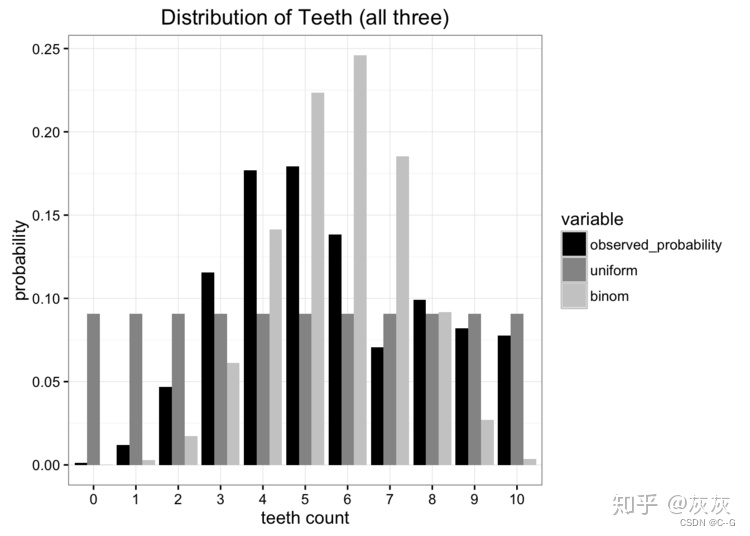
现如今有许多错误度量标准,但是我们主要关注的是必须使发送的信息量最少。这两个模型都将我们的问题所需的参数量减少。最好的方法是计算分布哪个保留了我们原始数据源中最多的信息。这就是Kullback-Leibler散度的作用。
KL散度又可称为相对熵,描述两个概率分布 P 和 Q 的差异或相似性,用 DKL(P∣∣Q)D_{KL}(P\left | \right |Q)DKL(P∣∣Q) 表示
DKL(P∣∣Q)=H(P,Q)−H(P)=∑iP(xi)log1Q(xi)−∑iP(xi)log1P(xi)=∑iP(xi)logP(xi)Q(xi)(7)\begin{aligned} D_{KL}(P || Q) & = H(P,Q) - H(P) \\ & = \sum_i P(x_i) \log \frac{1}{Q(x_i)} - \sum_i P(x_i) \log \frac{1}{P(x_i)} \\ & = \sum_i P(x_i) \log \frac{P(x_i)}{Q(x_i)} \tag{7} \\ \end{aligned} DKL(P∣∣Q)=H(P,Q)−H(P)=i∑P(xi)logQ(xi)1−i∑P(xi)logP(xi)1=i∑P(xi)logQ(xi)P(xi)(7)
很显然,散度越小,说明概率 Q 与概率 P 之间越接近,那么估计的概率分布与真实的概率分布也就越接近。
KL散度的性质:
- 非对称性:DKL(P∣∣Q)≠DKL(Q∣∣P)D_{KL}(P || Q) \neq D_{KL}(Q || P)DKL(P∣∣Q)=DKL(Q∣∣P)
- DKL(P∣∣Q)≥0D_{KL}(P || Q) \geq 0DKL(P∣∣Q)≥0,仅在 P=Q时等于0
性质2是很重要的,可以用 Jensen 不等式证明。
Jensen 不等式与凸函数是密切相关的。可以说 Jensen 不等式是凸函数的推广,而凸函数是 Jensen 不等式的特例。
相关文章:

14、KL散度
KL 散度,是一个用来衡量两个概率分布的相似性的一个度量指标。 现实世界里的任何观察都可以看成表示成信息和数据,一般来说,我们无法获取数据的总体,我们只能拿到数据的部分样本,根据数据的部分样本,我们会…...

TypeError: load() missing 1 required positional argument: ‘Loader‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...

【设计模式】 观察者模式介绍及C代码实现
【设计模式】 观察者模式介绍及C代码实现 背景 在软件构建过程中,我们需要为某些对象建立一种“通知依赖关系”,即一个对象(目标对象)的状态发生改变,所有的依赖对象(观察者对象)都将得到通知。…...
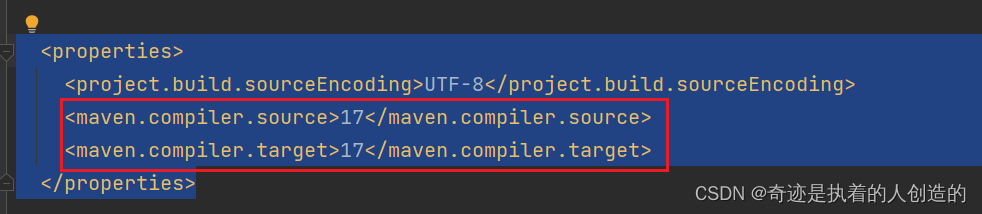
01-Maven基础-简介安装、基本使用(命令)、IDEA配置、(写jar,刷新自动下载)、依赖管理
文章目录0、Maven1、Maven 简介2、Maven 安装配置安装配置步骤3、Maven 基本使用Maven 常用命令Maven 生命周期IDEA 配置 MavenMaven 坐标详解IDEA 创建 Maven 项目IDEA 导入 Maven 项目配置 Maven-Helper 插件 (非常实用的小插件)依赖管理使用坐标导入 jar 包依赖范围0、Maven…...

一、前端稳定性规约该如何制定
前言 稳定性是数学或工程上的用语,判别一系统在有界的输入是否也产生有界的输出。若是,称系统为稳定;若否,则称系统为不稳定。 前端稳定性的体系建设大约可以分为了发布前,发布后,以及事故解决后三个阶段…...
Docker网络)
Docker(三)Docker网络
目录1 结论知识2 link3 自定义网络1 结论知识 每一个容器启动时都会被分配一个ip地址;宿主机可以ping通任何一个docker容器;启动docker之后,宿主机默认网卡docker0,启动容器在宿主机注册网卡,使用的evth-pair技术&…...

Js高级API
Decorator装饰器 针对属性 / 方法的装饰器 // decorator 外部可以包装一个函数,函数可以带参数function Decorator (type) {/*** 这里是真正的decorator* description: 装饰的对象的描述对象* target:装饰的属性所述类的原型,不是实例后的类。如果装饰…...
团队:在人身上,你到底愿意花多大精力?
你好,我是叶芊。 今天我们讨论怎么带团队这个话题,哎先别急着走,你可能跟很多人一样,觉得带团队离我还太远,或者觉得我才不要做管理,我要一路技术走到底,但是你知道吗?带团队做事&am…...

Linux-Poolkit提权
Linux-Poolkit提权 漏洞复现- Linux Polkit 权限提升漏洞(CVE-2021-4034) 0x00 前言 polkit是一个授权管理器,其系统架构由授权和身份验证代理组成,pkexec是其中polkit的其中一个工具,他的作用有点类似于sudo&#x…...

【React全家桶】React Hooks
React Hookshooks介绍useState(保存组件状态)useEffect()useCallback(记忆函数)useMemo() 记忆组件useRef(保存引用值)useReducer()useContext(减少组件层级)自定义hookshooks介绍 在react类组件(class)写法中,有setState和生命周期对状态进…...

CLIP论文阅读
Learning Transferable Visual Models From Natural Language Supervision 利用自然语言的监督信号学习可迁移的视觉模型 概述 迁移学习方式就是先在一个较大规模的数据集如ImageNet上预训练,然后在具体的下游任务上再进行微调。这里的预训练是基于有监督训练的&am…...
)
华为OD机试真题Python实现【身高排序】真题+解题思路+代码(20222023)
身高排序 题目 小明今年升学到了小学一年级, 来到新班级后,发现其他小朋友身高参差不齐, 然后就想基于各小朋友和自己的身高差,对他们进行排序, 请帮他实现排序 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 第一行为正整数H…...
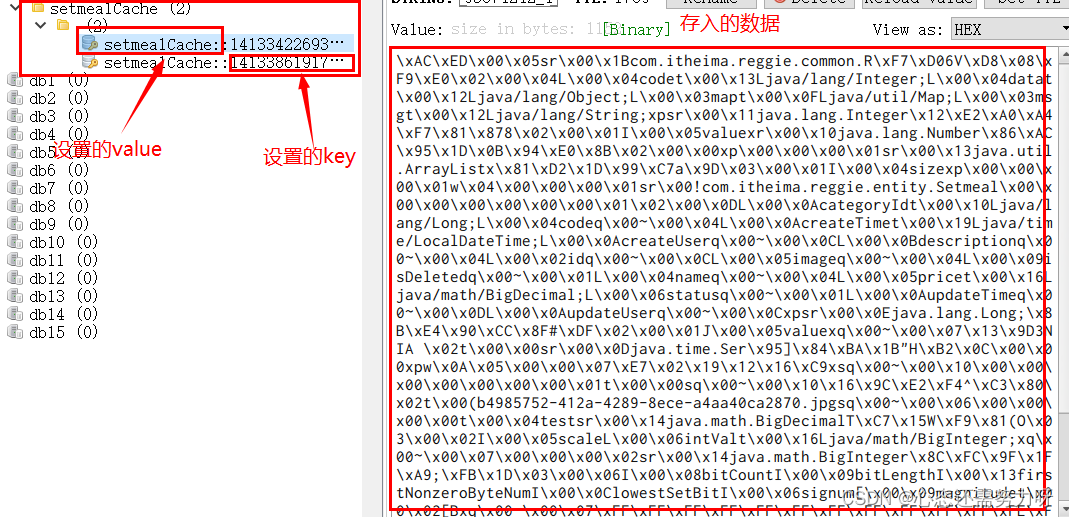
Spring Cache的使用--快速上手篇
系列文章目录 分页查询–Java项目实战篇 全局异常处理–Java实战项目篇 完善登录功能–过滤器的使用 更多该系列文章请查看我的主页哦 文章目录系列文章目录前言一、Spring Cache介绍二、Spring Cache的使用1. 导入依赖2. 配置信息3. 在启动类上添加注解4. 添加注解4.1 CacheP…...
MySQL是如何支持4种事务隔离级别的?Spring事务注解是如何设置的?)
(三十八)MySQL是如何支持4种事务隔离级别的?Spring事务注解是如何设置的?
上次我们讲完了SQL标准下的4种事务隔离级别,平时比较多用的就是RC和RR两种级别,那么在MySQL中也是支持那4种隔离级别的,基本的语义都是差不多的 但是要注意的一点是,MySQL默认设置的事务隔离级别,都是RR级别的&#x…...

【博学谷学习记录】大数据课程-学习第八周总结
Hadoop初体验 使用HDFS 1.从Linux本地上传一个文本文件到hdfs的/目录下 #在/export/data/目录中创建a.txt文件,并写入数据 cd /export/data/ touch a.txt echo "hello" > a.txt #将a.txt上传到HDFS的根目录 hadoop fs -put a.txt /2.通过页面查看…...
go cobra初试
cobra开源地址 https://github.com/spf13/cobra cobra是什么 Cobra is a library for creating powerful modern CLI applications. Cobra is used in many Go projects such as Kubernetes, Hugo, and GitHub CLI to name a few. This list contains a more extensive lis…...

【react全家桶】 事件处理
文章目录03 【事件处理】1.React事件2.类式组件绑定事件3.向事件处理程序传递参数4.收集表单数据5.受控和非受控组件5.函数的柯里化03 【事件处理】 React的事件是通过onXxx属性指定事件处理函数 React 使用的是自定义事件,而不是原生的 DOM 事件 React 的事件是通过…...

RabbitMQ交换机(Exchanges)
目录 一、概念 二、临时队列 三、绑定 四、Fanout(扇出交换机) (一)介绍 (二)实战 五、Direct(直接交换机) (一)介绍 (二)实…...

2023年java初级面试题10道基础试水题
1、面向对象的特征有哪些方面?答:面向对象的特征主要有以下几个方面:1)抽象:抽象是将一类对象的共同特征总结出来构造类的过程,包括数据抽象和行为抽象两方面。抽象只关注对象有哪些属性和行为,并不关注这些行为的细节…...

烙铁使用方法
烙铁使用 烙铁是硬件工程师最经常使用的工具之一,一把性能保持良好的烙铁能帮助我们快速进行电路调试。烙铁第一次加热时采用焊锡均匀涂覆在烙铁头上,以便去除包在烙铁头上面的氧化物。在工作中我们需要根据情况选择合适的烙铁头类型,合适的温度进行操作。完成焊接后要在烙铁…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
