【阅读笔记】SecureML: A System for ScalablePrivacy-Preserving Machine Learning
1. Motivation
针对机器学习中的出现的数据隐私泄露的风险,提出了线性回归、逻辑回归以及简单神经网络的隐私保护模型。
2. Contributions
2.1 为线性回归、逻辑回归以及神经网络设计安全计算协议
2.1.1.1 线性回归
线性回归损失函数为:
,
采用SGD算法处理损失函数,权重w的更新公式为:
式子只有加法、乘法运算,秘密分享的形式为:
写成向量的形式为:
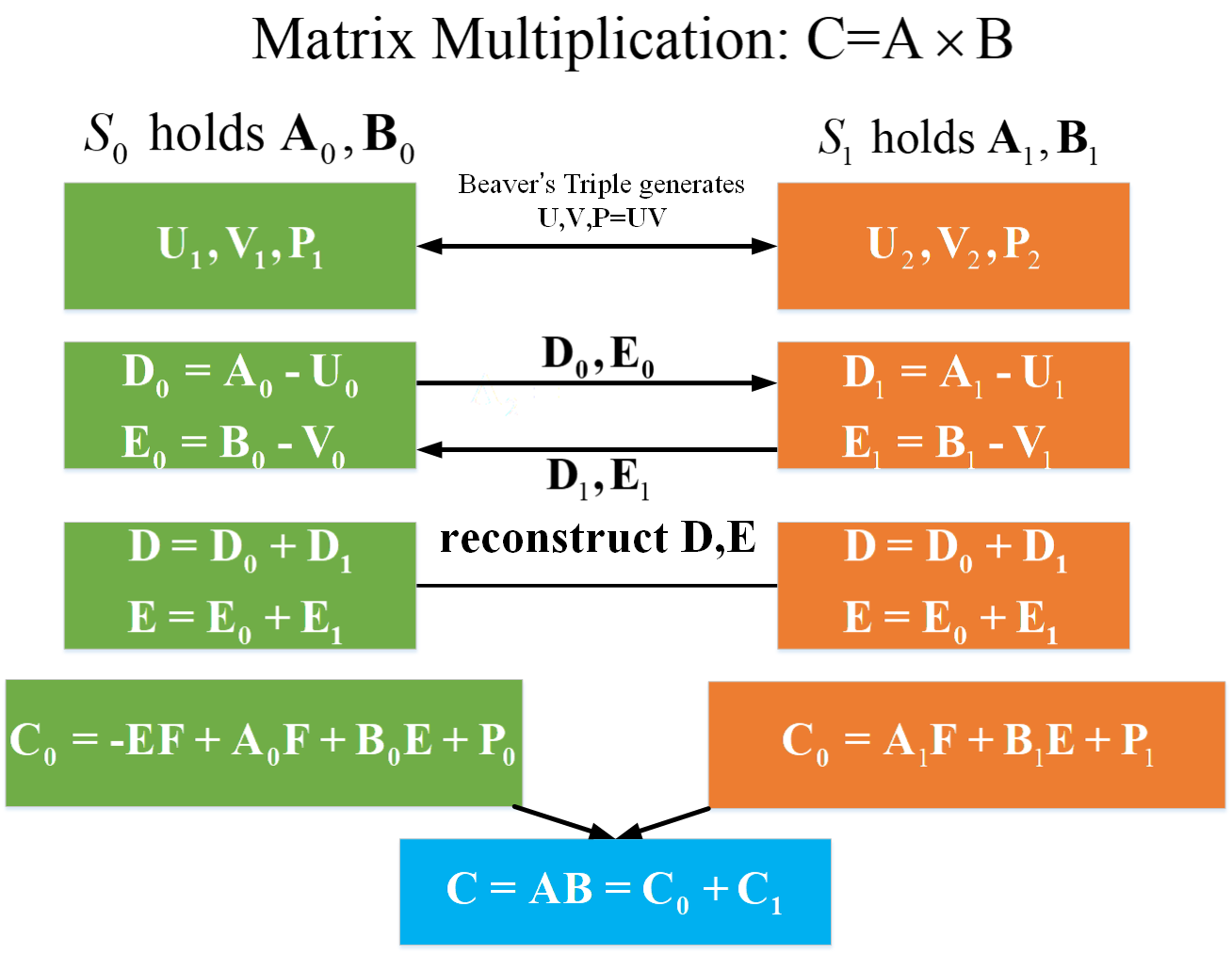
根据Beaver's triple 计算矩阵乘法:
这里需要注意的是文章中说明的是两个服务器
,都以获得数据的一个份额,并不是各方持有一份完整的数据。
可得:
,之后的乘法运算都依据这个式子。
完整过程如下:

2.2 运算中小数的处理
计算小数乘法,x*y,假设x和y都最多有D为小数。
(1)将x和y进行扩大
,
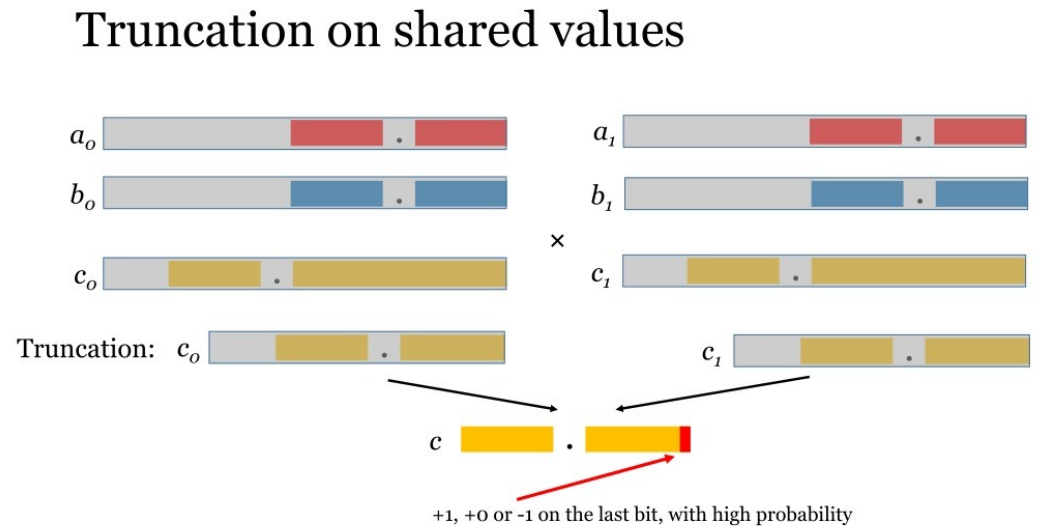
(2)截断小数
扩大后结果为,小数位数最多D为,所以将最后D位截取,截断后的结果可写为
,用
表示截断操作则最的相乘结果为
。
2.3 优化激活函数
在逻辑回归算法中,有函数,其中在实数域中,该函数包含的除法和求幂运算很难支持2PC和布尔运算,比之前工作用多项式去逼近函数不同的是,作者提出一个Friendly activation function,函数为f(u),f(u)图像如下图所示。

构造的灵感来源于:
(1)函数值应该收敛在0和1之间;(2)RELU函数
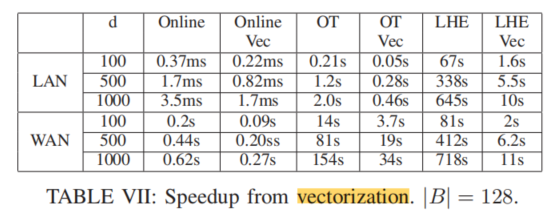
2.4 引入了面向秘密共享的向量化计算
线性回归下模型权重更新公式为,仅涉及加法和乘法。秘密分享形式下的加法在本地即可计算,而乘法需要借助Beavers Triple。但是元素级别的运算效率太低,这里优化为矩阵乘法
,由2.1节可知C的Share为:
,这样可以大大加快计算效率。
3. Q&R
3.1 为什么加法秘密共享是环上,shamir是在域上?
答:加法秘密分享只需要加减法就可以定义分享和恢复算法;shamir的恢复算法需要计算离散空间的除法,环中因为有些元素没有逆元,所以没法保证恢复算法能成功。域中元素都有逆元,可以计算除法。
3.2 隐私计算往往要求在有限域上运算,实际问题怎么去应用?
答:需要转化为将实际的运算转化到有限域的代数系统中。
4. Summary
优化一个问题,可以从各个方面入手,有的对结果有直接影响,有的是间接影响;有的直接影响大,有的直接影响小。
Reference
1.论文阅读笔记:SecureML: A System for Scalable Privacy-Preserving Machine Learning - 知乎
2.为什么不可以直接在实数上进行秘密分享? - 知乎 (zhihu.com)
相关文章:

【阅读笔记】SecureML: A System for ScalablePrivacy-Preserving Machine Learning
1. Motivation 针对机器学习中的出现的数据隐私泄露的风险,提出了线性回归、逻辑回归以及简单神经网络的隐私保护模型。 2. Contributions 2.1 为线性回归、逻辑回归以及神经网络设计安全计算协议 2.1.1.1 线性回归 线性回归损失函数为: , 采用SG…...

【2023美赛】C题Wordle预测27页中文论文及Python代码详解
【2023美赛】C题Wordle预测27页中文论文及Python详解 相关链接 (1)2023年美赛C题Wordle预测问题一建模及Python代码详细讲解 (2)2023年美赛C题Wordle预测问题二建模及Python代码详细讲解 (3)2023年美赛C题…...
【C++修行之路】STL——模拟实现string类
文章目录前言类框架构造与析构c_str迭代器操作符重载[]::> > < < !:reverse与resizereverseresizepush_back与append复用实现insert和erasec_str与流插入、流提取eraseswap(s1,s2)与s1.swap(s2)结语前言 这次我们分几个部分来实现string类…...
CorelDRAW2023最新版序列号使用教程
CorelDRAW2023用起来非常顺手,旨在为用户解决因在工作上带来的问题,在业内可谓享有极高的声誉,是业内人士常用的一款工具,有了它,可以更好的帮助用户把握好各个方面的细节,减少其他方面的失误,让…...

【一天一门编程语言】Python 语言程序设计极简教程
文章目录 Python 语言程序设计极简教程一、Python语言简介1.1 Python的优势1.2 Python的应用二、Python基础语法2.1 Python基础2.1.1 注释2.1.2 变量2.1.3 运算符2.1.4 控制流2.1.5 函数2.2 Python数据类型2.2.1 数字2.2.2 字符串2.2.3 列表2.2.4 元组2.2.4.1 元组的基本操作创…...
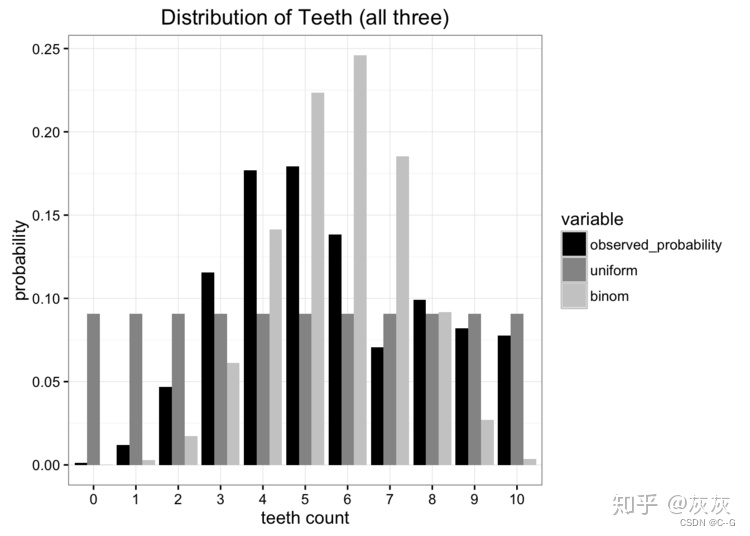
14、KL散度
KL 散度,是一个用来衡量两个概率分布的相似性的一个度量指标。 现实世界里的任何观察都可以看成表示成信息和数据,一般来说,我们无法获取数据的总体,我们只能拿到数据的部分样本,根据数据的部分样本,我们会…...

TypeError: load() missing 1 required positional argument: ‘Loader‘解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...

【设计模式】 观察者模式介绍及C代码实现
【设计模式】 观察者模式介绍及C代码实现 背景 在软件构建过程中,我们需要为某些对象建立一种“通知依赖关系”,即一个对象(目标对象)的状态发生改变,所有的依赖对象(观察者对象)都将得到通知。…...
01-Maven基础-简介安装、基本使用(命令)、IDEA配置、(写jar,刷新自动下载)、依赖管理
文章目录0、Maven1、Maven 简介2、Maven 安装配置安装配置步骤3、Maven 基本使用Maven 常用命令Maven 生命周期IDEA 配置 MavenMaven 坐标详解IDEA 创建 Maven 项目IDEA 导入 Maven 项目配置 Maven-Helper 插件 (非常实用的小插件)依赖管理使用坐标导入 jar 包依赖范围0、Maven…...

一、前端稳定性规约该如何制定
前言 稳定性是数学或工程上的用语,判别一系统在有界的输入是否也产生有界的输出。若是,称系统为稳定;若否,则称系统为不稳定。 前端稳定性的体系建设大约可以分为了发布前,发布后,以及事故解决后三个阶段…...
Docker网络)
Docker(三)Docker网络
目录1 结论知识2 link3 自定义网络1 结论知识 每一个容器启动时都会被分配一个ip地址;宿主机可以ping通任何一个docker容器;启动docker之后,宿主机默认网卡docker0,启动容器在宿主机注册网卡,使用的evth-pair技术&…...

Js高级API
Decorator装饰器 针对属性 / 方法的装饰器 // decorator 外部可以包装一个函数,函数可以带参数function Decorator (type) {/*** 这里是真正的decorator* description: 装饰的对象的描述对象* target:装饰的属性所述类的原型,不是实例后的类。如果装饰…...
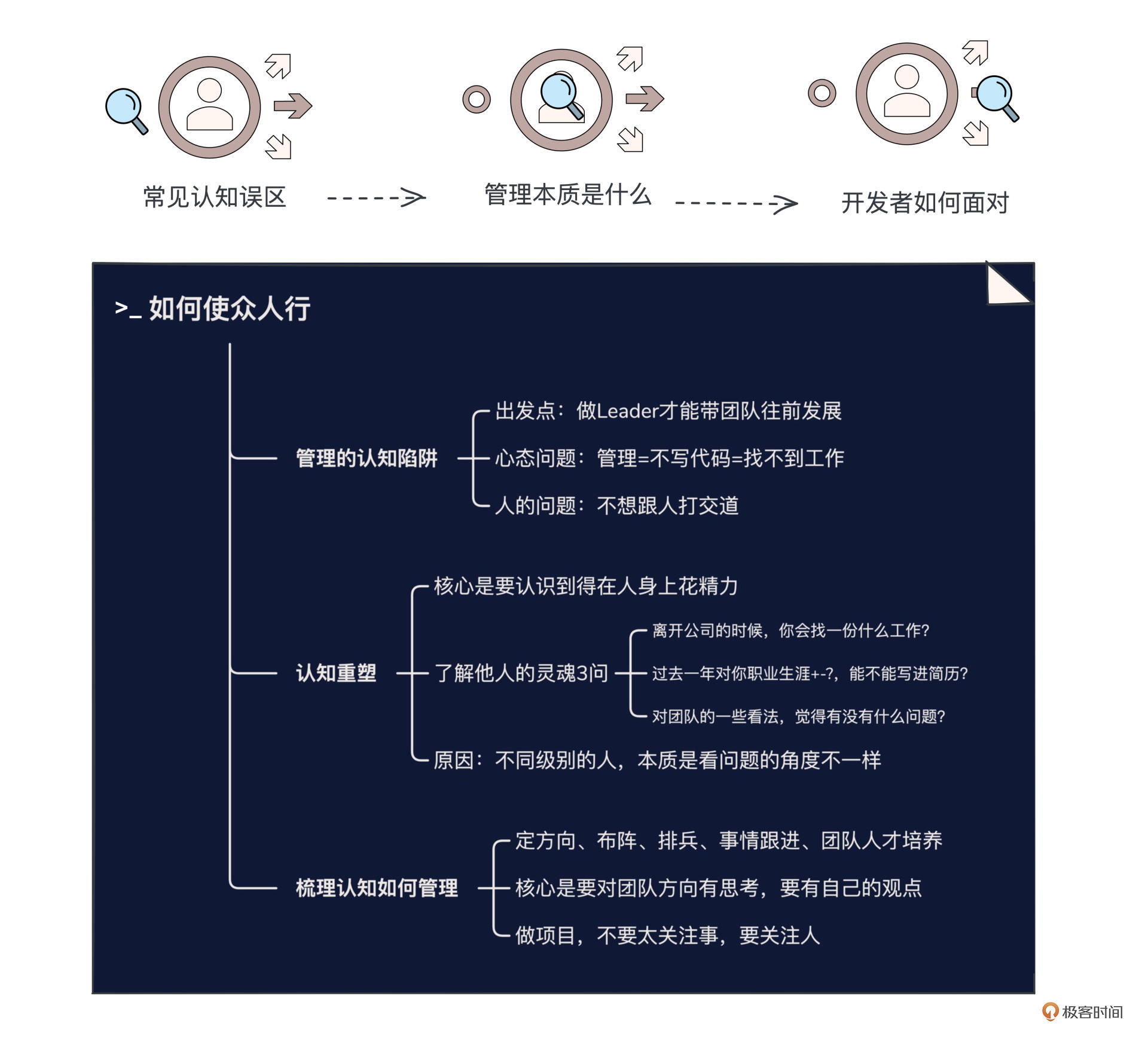
团队:在人身上,你到底愿意花多大精力?
你好,我是叶芊。 今天我们讨论怎么带团队这个话题,哎先别急着走,你可能跟很多人一样,觉得带团队离我还太远,或者觉得我才不要做管理,我要一路技术走到底,但是你知道吗?带团队做事&am…...

Linux-Poolkit提权
Linux-Poolkit提权 漏洞复现- Linux Polkit 权限提升漏洞(CVE-2021-4034) 0x00 前言 polkit是一个授权管理器,其系统架构由授权和身份验证代理组成,pkexec是其中polkit的其中一个工具,他的作用有点类似于sudo&#x…...

【React全家桶】React Hooks
React Hookshooks介绍useState(保存组件状态)useEffect()useCallback(记忆函数)useMemo() 记忆组件useRef(保存引用值)useReducer()useContext(减少组件层级)自定义hookshooks介绍 在react类组件(class)写法中,有setState和生命周期对状态进…...

CLIP论文阅读
Learning Transferable Visual Models From Natural Language Supervision 利用自然语言的监督信号学习可迁移的视觉模型 概述 迁移学习方式就是先在一个较大规模的数据集如ImageNet上预训练,然后在具体的下游任务上再进行微调。这里的预训练是基于有监督训练的&am…...
)
华为OD机试真题Python实现【身高排序】真题+解题思路+代码(20222023)
身高排序 题目 小明今年升学到了小学一年级, 来到新班级后,发现其他小朋友身高参差不齐, 然后就想基于各小朋友和自己的身高差,对他们进行排序, 请帮他实现排序 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 输入 第一行为正整数H…...
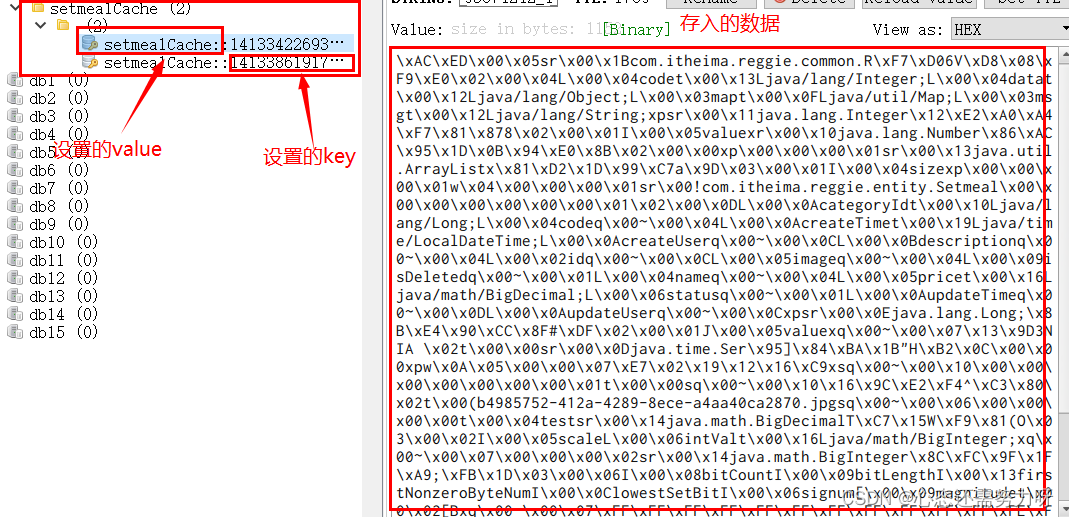
Spring Cache的使用--快速上手篇
系列文章目录 分页查询–Java项目实战篇 全局异常处理–Java实战项目篇 完善登录功能–过滤器的使用 更多该系列文章请查看我的主页哦 文章目录系列文章目录前言一、Spring Cache介绍二、Spring Cache的使用1. 导入依赖2. 配置信息3. 在启动类上添加注解4. 添加注解4.1 CacheP…...
MySQL是如何支持4种事务隔离级别的?Spring事务注解是如何设置的?)
(三十八)MySQL是如何支持4种事务隔离级别的?Spring事务注解是如何设置的?
上次我们讲完了SQL标准下的4种事务隔离级别,平时比较多用的就是RC和RR两种级别,那么在MySQL中也是支持那4种隔离级别的,基本的语义都是差不多的 但是要注意的一点是,MySQL默认设置的事务隔离级别,都是RR级别的&#x…...

【博学谷学习记录】大数据课程-学习第八周总结
Hadoop初体验 使用HDFS 1.从Linux本地上传一个文本文件到hdfs的/目录下 #在/export/data/目录中创建a.txt文件,并写入数据 cd /export/data/ touch a.txt echo "hello" > a.txt #将a.txt上传到HDFS的根目录 hadoop fs -put a.txt /2.通过页面查看…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...