CCF CCSP2023参赛记 + 算法题题解
大家好啊,时隔多年,作为大四老年人,再次来到这个地方记录算法竞赛相关,可能也是最后一次参加这种算法赛事了,我觉得还是很有纪念意义的。虽然我高中搞OI被强基背刺,以至于到了大学有点躲着竞赛,但是我还是对算法题有一种玩解谜游戏一样的兴趣的。
前年和去年都因为疫情原因,要么没能参加,要么只能线上参加,只能说比较遗憾。特别是去年线上参赛的那次,6个小时3道题,题目出的不咋地,唯一一道算法题正解是搜索剪枝,剩下两道系统题不管是大模拟还是什么,都没什么下手的空间,最后交样例骗了30分,还拿了块铜牌,不能说很光彩。今年总算是有机会,来到了沈阳师范大学参加线下比赛,原原本本的12小时5道题,终于不是阉割版了。同时这也是我人生中第一次参加长达12个小时的马拉松竞赛,不过赛程中途管吃管喝,虽然是盒饭,但还算不错了。
今年的题还是很有意思的,三道算法题,另外两道系统题都是那种没有性能比拼的模拟题,可以说是撞到我这个OI老顽童的爽点上了。从搞OI开始一路打铁、打铜、打银,现在总算是在这里圆了一个金牌梦了。不一定特别有含金量,但至少是个成就,也算是为我的算法竞赛生涯划上了一个比较让我满意的句号。
记录就记录这么多,呃呃,毕竟12小时都坐在一个地方,没啥可记录的也很正常,所以为了让这篇文章有点内容,还是讲讲这次的三道算法题,以及我的想法吧。为了让看到这篇文章的有机会自己想想题,我就把三道题题目大意先写出来,再给出各个题我的做法。
文章目录
- 题目大意
- T1:装修(decorate)
- T2:摸球(ball)
- T3:次元波动平衡(surge)
- 做法
- T1:装修(decorate)
- T2:摸球(ball)
- T3:次元波动平衡(surge)
题目大意
T1:装修(decorate)
有 M ( M ≤ 1 e 4 ) M(M\le 1e4) M(M≤1e4)种素材,其中某些可以直接花钱获取,成本各不相同( c i c_i ci),而其中某些只能用其它素材合成,一种素材最多在所有其它素材的合成表中出现一次,而且保证不会成环(也就是说合成关系的形状是森林)。除此之外,还可以通过和邻居交换,或者购买礼包的方式获得素材,共有 P ( P ≤ 5 ) P(P\le 5) P(P≤5)个邻居,每个邻居有一对 s j , r j s_j,r_j sj,rj,表示可以用一个 s j s_j sj素材换一个 r j r_j rj素材,而不需要其它额外成本,而另有 Q ( Q ≤ 5 ) Q(Q\le 5) Q(Q≤5)个礼包,可以支付一个固定成本 w i w_i wi来获得礼包中包含的多种素材,这些礼包中的素材总数也不超过 1 e 4 1e4 1e4这个级别。你可以和每位邻居交换最多一次,也可以购买每个礼包最多一次,求在所有这些条件下,要最终获得某 N N N种特定素材,所需要支付的最小成本。
T2:摸球(ball)
有 N N N种颜色的球各 a a a个,另有 M M M种颜色的球各 b b b个,同颜色的球编号为 1 1 1到 a a a(或 b b b),求在共 N + M N+M N+M种颜色的球中选取 k k k个不同颜色的球,其中任何编号出现次数都不超过 s s s次的方案数,结果模 998244353 998244353 998244353。 1 ≤ N , M , a , b , k ≤ 1 e 3 , 1 ≤ s ≤ 2 1\le N,M,a,b,k\le 1e3, 1\le s\le 2 1≤N,M,a,b,k≤1e3,1≤s≤2。
T3:次元波动平衡(surge)
A A A是一个长为 N N N的数列,要求选取其中最多 K K K个位置减去一个数 D D D,得到新的数列 a a a,最小化所有子段和的最大值,也就是最小化 max l ≤ r ∑ i = l r a i \max_{l\le r}\sum_{i=l}^ra_i maxl≤r∑i=lrai,求这个最小值。 K ≤ N ≤ 5 e 5 , 1 ≤ D ≤ 1 0 9 , − 1 0 9 ≤ A i ≤ 1 0 9 K\le N\le 5e5, 1\le D\le 10^9, -10^9\le A_i \le 10^9 K≤N≤5e5,1≤D≤109,−109≤Ai≤109。
做法
T1:装修(decorate)
这是一道思维题。
可以先考虑没有邻居可以交换,也没有礼包可以购买的情况。显然,需要的材料如果需要合成的话,就肯定需要把所有合成需要的材料(子树中所有叶子)购买一份,因此计算成本也很简单,自顶向下扫一遍森林,把需求pushdown到每个叶子上,看一下每个叶子被算了几遍,把成本加起来即可,复杂度 O ( M ) O(M) O(M)。
接下来考虑可以交换的情况,由于进行交换的方案数很小,一共也就是 2 P ≤ 32 2^P\le 32 2P≤32种(每个邻居可以交换0次或1次),所以就直接暴搜和哪些邻居交换,然后把交换需要的前置素材加入需求,而交换获得的素材可以看成是“负”的需求(因为多出来了),它可以抵消掉一个从祖先节点来的需求(也就是用获得的这个素材来直接进行祖先节点的合成,不用再买它的所有合成素材了),但不能抵消儿孙节点的需求(因为只能往上合成,不能往下“拆分”),因此在自顶向下扫描的时候,正的需求就pushdown,负的需求就不pushdown就可以了。这个我没有严格证明,但既然A了,那应该就是对的。这样扫描一次仍然是 O ( M ) O(M) O(M),扫描 2 P 2^P 2P次就可以解决。
加上礼包的思路也差不多,将购买礼包的方案和交换方案一起暴搜,一共有 2 P + Q ≤ 1024 2^{P+Q}\le 1024 2P+Q≤1024种情况,而购买礼包就是直接增加一部分成本,外加直接获得一部分素材,也作为负的需求加到节点上即可,然后扫描还是和之前一样,这样整个解法的复杂度是 O ( 2 P + Q M ) O(2^{P+Q}M) O(2P+QM),可以解决此题。
T2:摸球(ball)
这道题很明显是一道组合数学题。
s = 1 s=1 s=1和 s = 2 s=2 s=2的情况很显然非常不同,所以先考虑 s = 1 s=1 s=1,也就是每种编号最多出现一次的情况。
s = 1 s=1 s=1的情况
不妨设 a < b a<b a<b,如果 a > b a>b a>b就同时交换 N , M N,M N,M和 a , b a,b a,b,显然是等价的。假设前 N N N种颜色的球中取 i i i个,那么后 M M M种颜色的球中就要取 k − i k-i k−i个,前面那 i i i个的取法种数是 C N i × C a i × i ! C_N^i\times C_a^i\times i! CNi×Cai×i!,而对于后面那 k − i k-i k−i个,由于前 i i i个球的编号一定都在 [ 1 , a ] [1,a] [1,a]内,所以后 k − i k-i k−i个球的编号可取范围就少了 i i i个,因此固定一种前 i i i个球的取法,后 k − i k-i k−i个球的取法总数总是 C M k − i × C b − i k − i × ( k − i ) ! C_M^{k-i}\times C_{b-i}^{k-i}\times (k-i)! CMk−i×Cb−ik−i×(k−i)!。
总结起来:
答案: a n s = ∑ i = 0 k C N i C a i C M k − i C b − i k − i ⋅ i ! ( k − i ) ! ans=\sum_{i=0}^k C_N^iC_a^iC_M^{k-i}C_{b-i}^{k-i}\cdot i!(k-i)! ans=∑i=0kCNiCaiCMk−iCb−ik−i⋅i!(k−i)!
O ( ( N + M ) 2 ) O((N+M)^2) O((N+M)2)预处理一下所有组合数和阶乘即可 O ( k ) O(k) O(k)计算答案。
s = 2 s=2 s=2的情况
对于 s = 2 s=2 s=2的情况,之前我们是将要取的球按颜色分成两部分,然后组合,现在这个情况,将要取的球按编号分成两部分比较好。还是设 a < b a<b a<b,假设编号 [ 1 , a ] [1,a] [1,a]中的球共取了 i i i个,要求每种编号出现至多两次的方案数,还是不太好算,所以考虑再枚举一个 r r r,表示恰好有 r r r个编号出现了两次,其它编号都只出现一次。令 g ( i , r ) g(i,r) g(i,r)为下列子问题的方案数:
子问题 g ( i , r ) g(i,r) g(i,r): 假设已经选定了要取的 i i i个球的颜色集合(一定是 i i i种颜色),而且选定了出现两次的编号集合(共 r r r个编号),以及出现一次的编号集合(共 i − 2 r i-2r i−2r个编号),这种情况下的方案数。
要计算这个子问题的答案,首先考虑从 i i i种颜色中选择 i − r i-r i−r个算作“首次出现”的颜色集合,而剩下 r r r个算作“重复出现”的颜色集合,选择数为 C i i − r = C i r C_i^{i-r}=C_i^r Cii−r=Cir,然后两个部分具体编号就可以自己任意排列了,也就是乘上 r ! ( i − r ) ! r!(i-r)! r!(i−r)!。但这样算出来的方案会有重复,对于每一种方案,由于一共有 r r r个重复编号,每个编号对应的两种颜色,每一种都有可能被当作“重复出现”的那一次,所以总的来说,每个方案会被 2 r 2^r 2r种“重复出现”的颜色集合算到,所以将上述求出的方案数除以 2 r 2^r 2r就是正确的方案数。即:
g ( i , r ) = 1 2 r ⋅ C i r ⋅ r ! ( i − r ) ! = 1 2 r ⋅ i ! g(i,r)=\frac{1}{2^r}\cdot C_i^r \cdot r! (i-r)!=\frac{1}{2^r}\cdot i! g(i,r)=2r1⋅Cir⋅r!(i−r)!=2r1⋅i!
那么我们其实可以算没有之前说的那些“假定”,单纯从 N + M N+M N+M个颜色中选出 i i i个球,恰有 r r r个编号重复的情况的方案数了。我们发现选择颜色集合、选择 r r r个重复编号、选择 i − 2 r i-2r i−2r个不重复编号这几个决策互相独立,所以方案数可以直接相乘,所以总的方案数为:
C N + M i ⋅ C a r ⋅ C a − r i − 2 r ⋅ g ( i , r ) C_{N+M}^i\cdot C_a^r\cdot C_{a-r}^{i-2r}\cdot g(i,r) CN+Mi⋅Car⋅Ca−ri−2r⋅g(i,r)
接下来考虑一下剩下那 k − i k-i k−i个球怎么选。这些球的编号在 [ a + 1 , b ] [a+1,b] [a+1,b]区间,只能在后 M M M种颜色中选,编号是不可能和前 i i i个球重复了,但颜色可能重复。没办法,再设定一个 t t t,表示前 i i i个球中有 t t t个球从后 M M M种颜色中选的方案数。所以之前说的第一部分总方案数不太准确,正确的方案数应该为:
固定 t , r t,r t,r,前 i i i个球的选取方案数: a n s 1 ( i , t , r ) = C N i − t ⋅ C M t ⋅ C a r ⋅ C a − r i − 2 r ⋅ g ( i , r ) ans_1(i,t,r)=C_N^{i-t}\cdot C_M^t\cdot C_a^r\cdot C_{a-r}^{i-2r}\cdot g(i,r) ans1(i,t,r)=CNi−t⋅CMt⋅Car⋅Ca−ri−2r⋅g(i,r)
那么后 k − i k-i k−i个球的方案数就也可以算了,推公式的方法和之前类似,这里直接给出公式:
固定 t , r ′ t,r' t,r′,后 k − i k-i k−i个球的选取方案数: a n s 2 ( i , t , r ′ ) = C M − t k − i ⋅ C b − a r ′ ⋅ C b − a − r ′ k − i − 2 r ′ ⋅ g ( k − i , r ′ ) ans_2(i,t,r')=C_{M-t}^{k-i}\cdot C_{b-a}^{r'}\cdot C_{b-a-r'}^{k-i-2r'}\cdot g(k-i,r') ans2(i,t,r′)=CM−tk−i⋅Cb−ar′⋅Cb−a−r′k−i−2r′⋅g(k−i,r′)
注意这里的 r ′ r' r′不同于之前的 r r r,虽然意义和之前的 r r r相似,但这里 r ′ r' r′描述的是后 k − i k-i k−i个球中重复编号的数目。
这样最终答案也可以算出了:
答案: a n s = ∑ i = 0 k ∑ t = 0 i ( ∑ r a n s 1 ( i , t , r ) ) × ( ∑ r ′ a n s 2 ( i , t , r ′ ) ) ans=\sum_{i=0}^k\sum_{t=0}^i(\sum_{r}ans_1(i,t,r))\times (\sum_{r'}ans_2(i,t,r')) ans=∑i=0k∑t=0i(∑rans1(i,t,r))×(∑r′ans2(i,t,r′))
至于怎么算这个玩意,预处理组合数和阶乘肯定是需要的,也需要预处理所有的 1 2 r \frac{1}{2^r} 2r1,可以使用欧拉定理等方法求逆元,这部分只要不超过 O ( ( N + M ) 2 ) O((N+M)^2) O((N+M)2)就不算瓶颈。而即使预处理,这个式子要直接算也是 O ( k 3 ) O(k^3) O(k3)的,注意到不管是 a n s 1 ans_1 ans1还是 a n s 2 ans_2 ans2,里面和 t t t有关的乘项以及和 r / r ′ r/r' r/r′有关的乘项都是完全分离的,所以一个 a n s 1 ( i , t , r ) ans_1(i,t,r) ans1(i,t,r)其实可以分成诸如 a n s 1 a ( i , t ) ⋅ a n s 1 b ( i , r ) ans_{1a}(i,t)\cdot ans_{1b}(i,r) ans1a(i,t)⋅ans1b(i,r)这种形式, a n s 2 ans_2 ans2同理,那么简单转化一下和式就有:
答案(计算用): a n s = ∑ i = 0 k ∑ t = 0 i a n s 1 a ( i , t ) ⋅ a n s 2 a ( i , t ) ⋅ ( ∑ r a n s 1 b ( i , r ) ) ⋅ ( ∑ r ′ a n s 2 b ( i , r ′ ) ) ans=\sum_{i=0}^k\sum_{t=0}^ians_{1a}(i,t)\cdot ans_{2a}(i,t)\cdot (\sum_{r}ans_{1b}(i,r))\cdot (\sum_{r'}ans_{2b}(i,r')) ans=∑i=0k∑t=0ians1a(i,t)⋅ans2a(i,t)⋅(∑rans1b(i,r))⋅(∑r′ans2b(i,r′))
这样 a n s 1 a , a n s 1 b , a n s 2 a , a n s 2 b ans_{1a},ans_{1b},ans_{2a},ans_{2b} ans1a,ans1b,ans2a,ans2b都可以 O ( k 2 ) O(k^2) O(k2)计算,而只要在这个过程中同时预处理里面的那两个枚举 r r r的和式,最后这个总的和式就也可以 O ( k 2 ) O(k^2) O(k2)计算了。这样我们就终于解决了这一题。
T3:次元波动平衡(surge)
本题需要用到二分答案+贪心+数据结构优化。
首先注意到本题的答案是可二分的,即,如果 a n s ans ans是合法的答案,那么 ≥ a n s \ge ans ≥ans的答案也都是合法的,于是考虑二分答案,转变为判定问题:给定一个数 a n s ans ans,判定能不能在给定修改次数 K K K内让所有子段和都 ≤ a n s \le ans ≤ans。
对这个问题我们可以使用贪心的思想。先考虑子段 [ 1 , 1 ] [1,1] [1,1],只有修改 A 1 A_1 A1才能影响这个子段,也就是说,如果它的子段和就 > a n s >ans >ans,那就必须修改 A 1 A_1 A1,而如果把 A 1 A_1 A1减 D D D了还是不行,那就再也不行了。而如果可以,或者一开始就不需要修改,那就把右端点右移,看下一步。假设现在我们在查看右端点为 r r r的所有子段,如果其中有 > a n s >ans >ans的值,只能通过修改 A 1 A_1 A1到 A r A_r Ar中的值解决。如果都可以改,那么先改 A r A_r Ar一定最优,因为算法运行到这,所有右端点 < r <r <r的子段肯定都没用了,而先修改 A r A_r Ar,能影响到的子段数量最多,从 [ 1 , r ] [1,r] [1,r]到 [ r , r ] [r,r] [r,r]的子段和都减了 D D D;而如果改一次还不够,那就往左顺延,看最右边的还没修改的是谁,把它改掉,这样肯定是最优的。我们可以直接找到最大的子段和,然后用其计算至少需要 − D -D −D的次数,然后就按照这个策略逐个找到这么多个减 D D D的位置,这样一来,最后无非就是几种结果:成功修改了子段和,而且修改次数没超过 K K K;成功修改了子段和,但是次数超过了 K K K;未能成功修改子段和。第一种情况表示 a n s ans ans是合法答案,第二种则反之,而如果在处理任何一个 r r r时,修改指定次数之后还是不能让所有子段和 ≤ a n s \le ans ≤ans,那么最后一定会被归到第三种情况,也是一个非法的情况。这样一来,整个算法最多只需要最后检查一次所有子段和即可,而不需要进行中间检查,就可以进行判定。
当然这个贪心直接模拟的话复杂度很高,所以需要使用数据结构优化。我们来总结一下我们需要做些什么:查询所有右端点为 r r r的端点的最小值;查询 r r r之前的最右边的没有被修改的点。第二个问题因为需要维护的点的插入和删除都在右端,因此用一个栈就可以解决,而第一个问题,可以把子段和看成两个端点的前缀和之差( s u m ( l , r ) = s u m ( 1 , r ) − s u m ( 1 , l − 1 ) sum(l,r)=sum(1,r)-sum(1,l-1) sum(l,r)=sum(1,r)−sum(1,l−1)),这样问题就变成了维护最小的 s u m ( 1 , l − 1 ) sum(1,l-1) sum(1,l−1),不仅要维护在末尾的插入(比如计算完了右端点为 r r r的情况,那么 s u m ( 1 , r ) sum(1,r) sum(1,r)也要被加入考虑范围),还要维护修改一个 A i A_i Ai产生的影响。每次修改 A i A_i Ai,从 s u m ( 1 , i ) sum(1,i) sum(1,i)到 s u m ( 1 , n ) sum(1,n) sum(1,n)都会全部 − D -D −D。区间修改和区间最值,你应该可以自然想到要用线段树解决了,时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),但这个复杂度在结合最外层的二分之后仍然不可接受,我们需要一个线性的算法来处理这个贪心。
注意到整个算法其实只需要维护当前所有考虑范围内的前缀和的最小值,而随着不断修改,这个值只会越来越小,所以我们只需要将任何时候产生的可能的新的最小值和原来的最小值进行比较,即可维护出这个值,甚至不需要知道产生这个值的位置。这里其实有多种线性或接近线性的方法可以进行维护,比如并查集,但是我用的栈的方法是严格线性的,就还是用之前用来存未修改过的 A i A_i Ai位置的栈,只不过栈中每个位置多存一个元素,表示从当前位置开始,到向栈顶方向的下一个元素之间这一段,产生的最小的前缀和值,这样一来,入栈时,新的一个前缀和可以用一开始预处理的前缀和,减去已经修改过的次数 × D \times D ×D来得出,弹栈时,栈顶代表的段中的所有前缀和被 − D -D −D,所以最小值就是原来段的最小值 − D -D −D,然后将这一段和栈顶之下那一段合并,最小值直接取 min \min min即可。由于每个位置最多入栈、出栈各一次,所以该方法是 O ( n ) O(n) O(n)的。
之前说过贪心最后还需要再检查一次所有子段和是不是都满足了要求,这个我们既然都知道了所有修改的位置,可以直接求出 a a a并从左到右扫描,一边扫一边记录最小的前缀和,然后用当前位置的前缀和减去这个最小,得到以当前位置为右端点的子段和中最大的值,以此得到所有子段和中的最大值,这样的时间复杂度也是 O ( n ) O(n) O(n)的。结合外层的二分答案,我们就解决了这一题。
写的时候要注意二分答案的界涉及正数和负数,正负数由于除法的归约方向不一样,所以最后的终止判定有点说道,要小心谨慎。
相关文章:

CCF CCSP2023参赛记 + 算法题题解
大家好啊,时隔多年,作为大四老年人,再次来到这个地方记录算法竞赛相关,可能也是最后一次参加这种算法赛事了,我觉得还是很有纪念意义的。虽然我高中搞OI被强基背刺,以至于到了大学有点躲着竞赛,…...
buuctf_练[GYCTF2020]FlaskApp
[GYCTF2020]FlaskApp 文章目录 [GYCTF2020]FlaskApp常用绕过方法掌握知识解题思路解题一 -- 计算pin码解题二 -- 拼接绕过 执行命令 关键paylaod 常用绕过方法 ssti详解与例题以及绕过payload大全_ssti绕过空格_HoAd’s blog的博客-CSDN博客 CTF 对SSTI的一些总结 - FreeBuf网…...

针对element-plus,跳转jump(快速翻页)
待补充 const goToPage () > {const inputElement document.querySelector(.el-pagination .el-input__inner);console.log(inputElement, inputElement); } 打印之后可以看到分页跳转的数字输入框,是有进行处理的,max"102",是我自己的…...
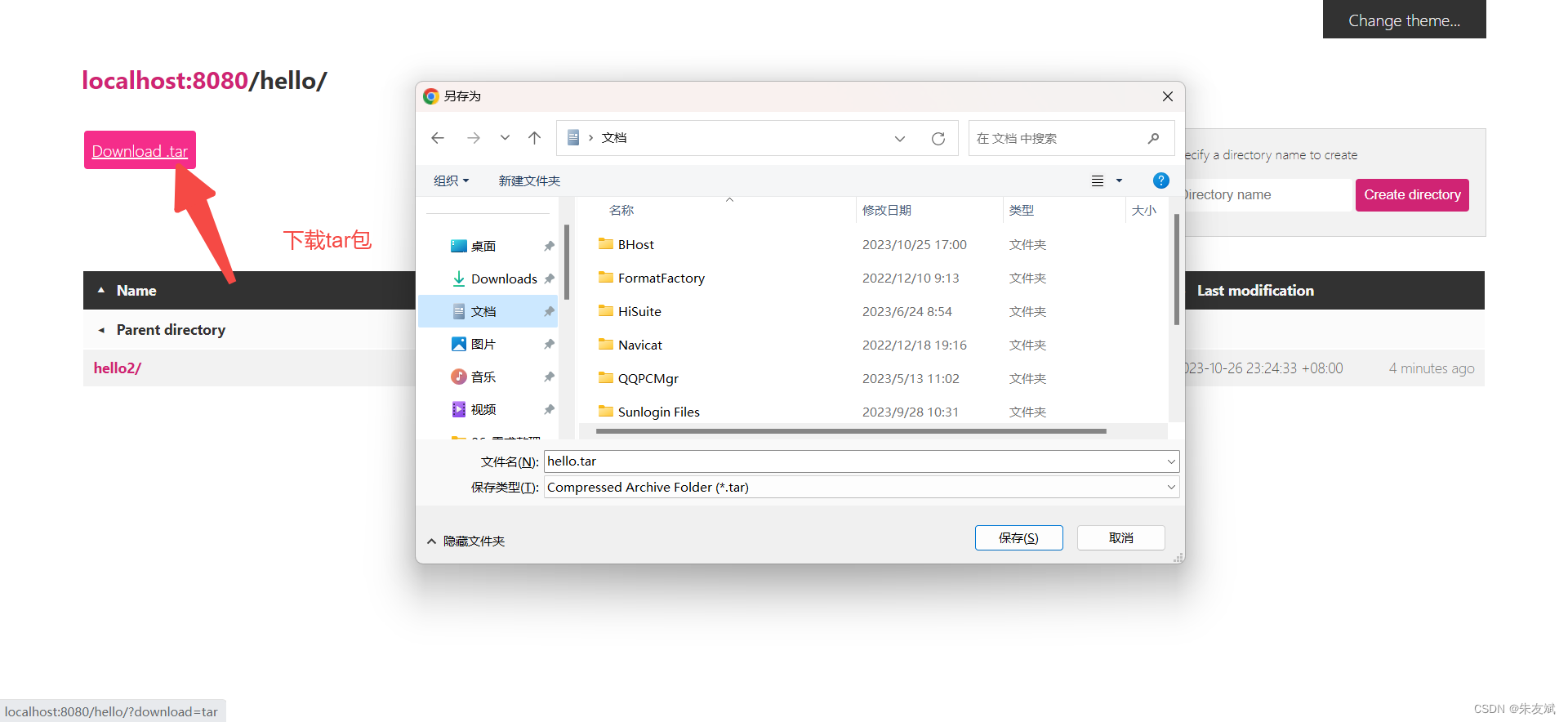
【软件安装】Windows系统中使用miniserve搭建一个文件服务器
这篇文章,主要介绍如何在Windows系统中使用miniserve搭建一个文件服务器。 目录 一、搭建文件服务器 1.1、下载miniserve 1.2、启动miniserve服务 1.3、指定根目录 1.4、开启访问日志 1.5、指定启动端口 1.6、设置用户认证 1.7、设置界面主题 (…...

iOS .a类型静态库使用终端进行拆解和合并生成
项目中会用到许多第三方的.a类型的静态库,有时候会有一些静态库回包含相同文件而产生冲突,我们就需要对这个库进行去重的一个操作。一般有哪些文件冲突了,xcode报错都会有详细的提示。我们可以将这两个库合并,也可以其中一方中的文…...

react-组件间的通讯
一、父传子 父组件在使用子组件时,提供要传递的数据子组件通过props接收数据 class Parent extends React.Component {render() {return (<div><div>我是父组件</div><Child name"张" age{16} /></div>)} }const Child …...

【广州华锐互动】VR公司工厂消防逃生演练带来沉浸式的互动体验
在工业生产过程中,安全问题始终是我们不能忽视的重要环节。特别是火灾事故,不仅会造成重大的经济损失,更会威胁到员工的生命安全。传统的消防安全训练方法,如讲座、实地演练等,虽然具有一定的效果,但是无法…...
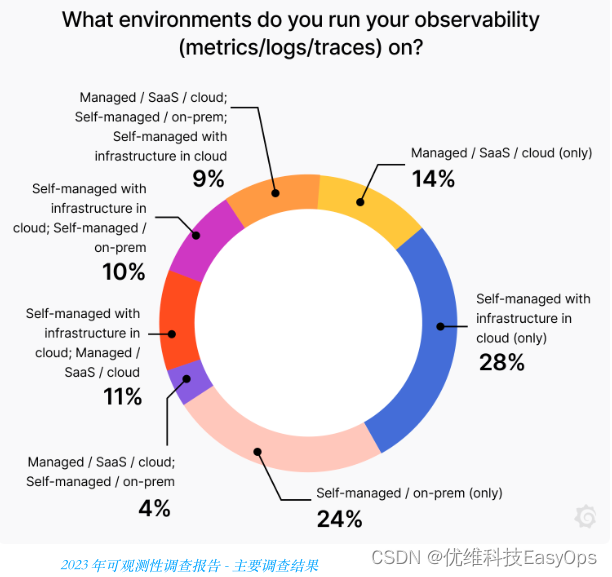
可观察性支柱:探索日志、指标和跟踪
通过检查系统输出来测量系统内部状态的能力称为可观察性。当可以仅使用输出信息(即传感器数据)来估计当前状态时,系统就变得“可观察”。您可以使用来自 Observability 的数据来识别和解决问题、优化性能并提高安全性。 在接下来的几节中&am…...

nginx浏览器缓存和上流缓存expires指令_nginx配置HTTPS
1.nginx控制浏览器缓存是针对于静态资源[js,css,图片等] 1.1 expires指令 location /static {alias/home/imooc;#设置浏览器缓存10s过期expires 10s;#设置浏览器缓存时间晚上22:30分过期expires @22h30m;#设置浏览器缓存1小时候过期expires -1h;#设置浏览器不缓存expires …...
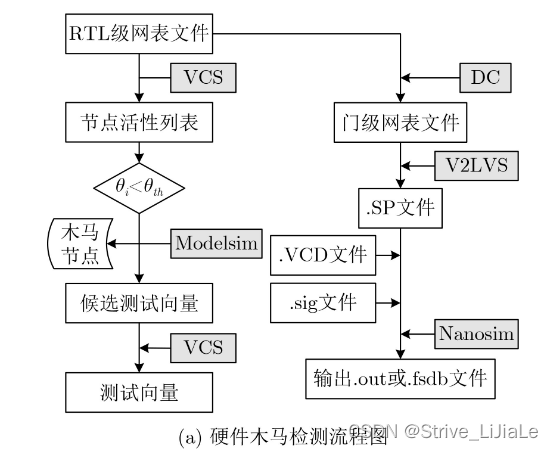
硬件安全与机器学习的结合
文章目录 1. A HT Detection and Diagnosis Method for Gate-level Netlists based on Machine Learning摘要Introduction 2. 基于多维结构特征的硬件木马检测技术摘要Instruction 3. A Hardware Trojan Detection and Diagnosis Method for Gate-Level Netlists Based on Diff…...
腾讯云国际-如何使用对象存储COS在 CKafka 控制台创建数据异步拉取任务?腾讯云代充
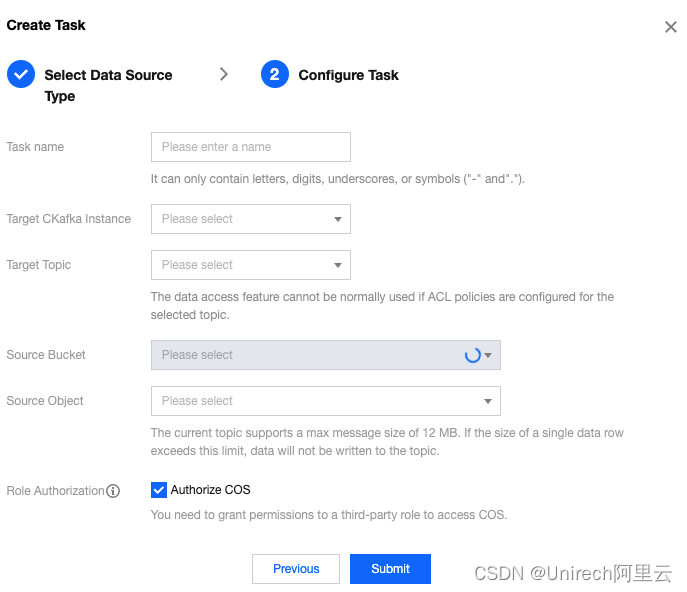
操作场景 Datahub 支持接入各种数据源产生的不同类型的数据,统一管理,再分发给下游的离线/在线处理平台,构建清晰的数据通道。 本文以 COS 数据为例介绍如何在 CKafka 控制台创建数据异步拉取任务,并对任务进行修改配置…...
内存马概念
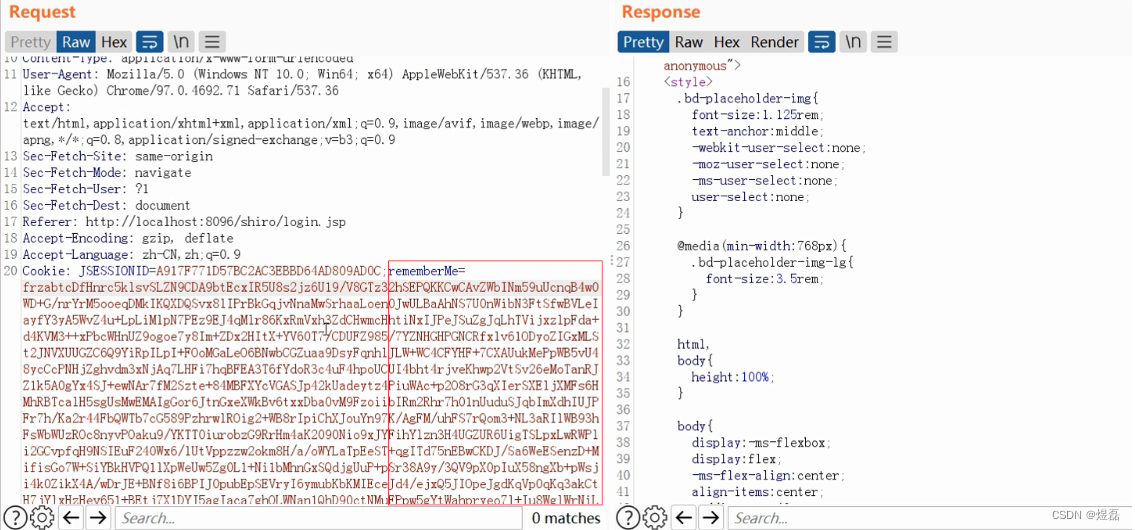
内存马概念 文章目录 内存马概念木马演变内存使用条件内存缺点JAVA Web三大组件Listener:监听器servelet请求流程内存马分类内存演示内存马植入方式案例shiro反序列化漏洞植入内存马 木马演变 内存使用条件 1. 禁止外联 2. 文件监控、查杀 3. spring Boot,不支持js…...
交换机基础(四):MSTP负载均衡配置案例
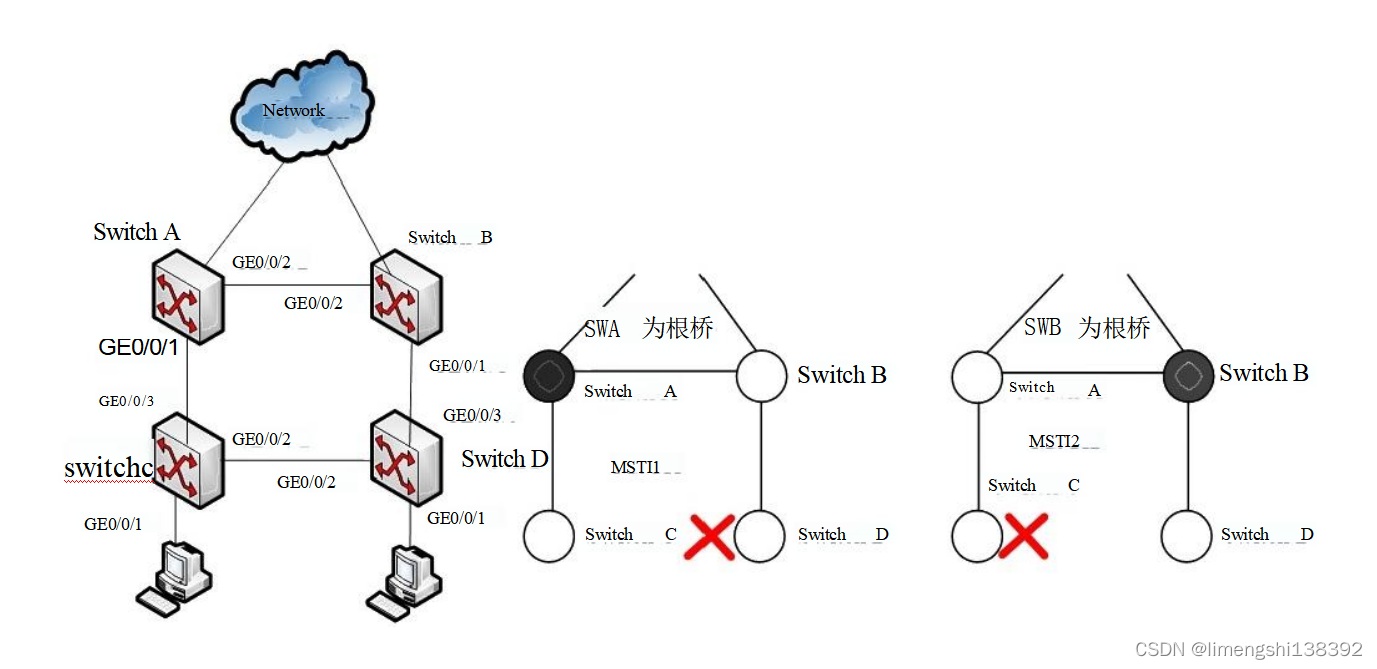
如图所示是某个企业内部核心网络的结构图,目前企业中有20个VLAN, 编号为VLAN1~VLAN20, 为了确保内部网络的可靠性,使用 了冗余链路和MSTP 协议。为了能更好地利用网络资源和带宽,现管理员希望通过配置MSTP 的负载均衡实现网络带宽…...
C# OpenCvSharp Yolov8 Face Landmarks 人脸特征检测
效果 项目 代码 using OpenCvSharp; using OpenCvSharp.Dnn; using System; using System.Collections.Generic; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms;namespace OpenCvSharp_Yolov8_Demo {public partial class frmMain…...
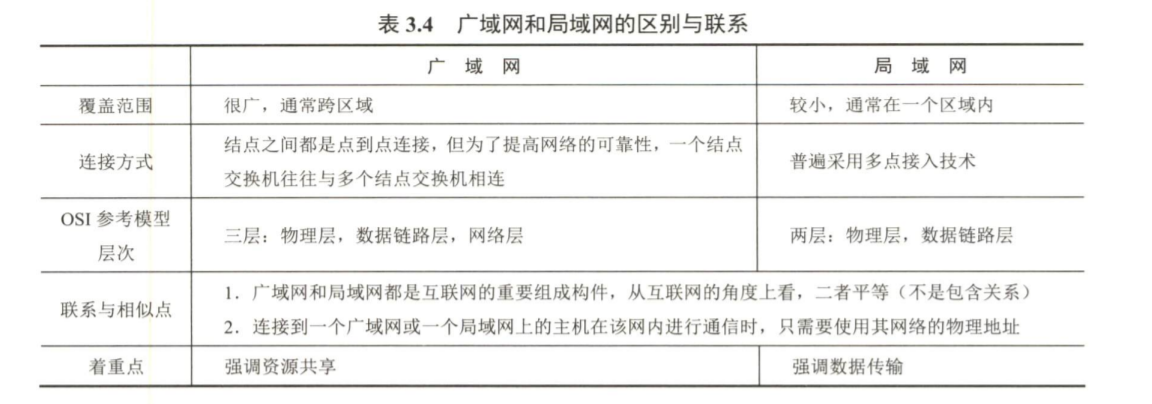
计算机网络之数据链路层(全)
[复习提示] 王道:本章是历年考试中考查的重点。要求在了解数据链路层基本概念和功能的基础上,重点掌握滑动窗口机制、三种可靠传输协议、各种MAC协议、HDLC协议和PPP协议,特别是CSMA/CD协议和以太网帧格式,以及局域网的争用期和最…...

前端TypeScript学习-交叉类型与泛型
交叉类型和泛型是TypeScript中的两个重要概念。 交叉类型(&)可以用来组合多个接口,形成一个新接口。它类似于接口继承(extends),但有一些区别。交叉类型不会产生类型继承层次结构,而是将多…...

科聪协作(复合)移动机器人整体解决方案
协作(复合)移动机器人(AGV/AMR)相较传统工业机器人具有更加安全和简单的工作优势,具备较强的发展潜力。协作(复合)移动机器人安全性和操作的简洁性、灵活性不断提高,优势得到了充分发挥,在越来越…...
RTE(Runtime Environment)
RTE(Runtime Environment)是一个运行时环境,在这个环境里,你可以实现的功能是: 作为一个缓冲buffer给应用层和BSW层的接口(例如COM)用来存储数据,也就是说定义一个全局变量供上层和下…...

搭建自己的搜索引擎——oh-my-search使用
搭建自己的搜索引擎——oh-my-search使用 使用elasticsearch和search-ui搭建自己的搜索引擎,快速查找资源和文件。如果对代码感兴趣,相关代码已在github上开源,欢迎fork代码。 搭建elasticsearch 先搭建eleasticsearch再搭建kibana 搭建e…...
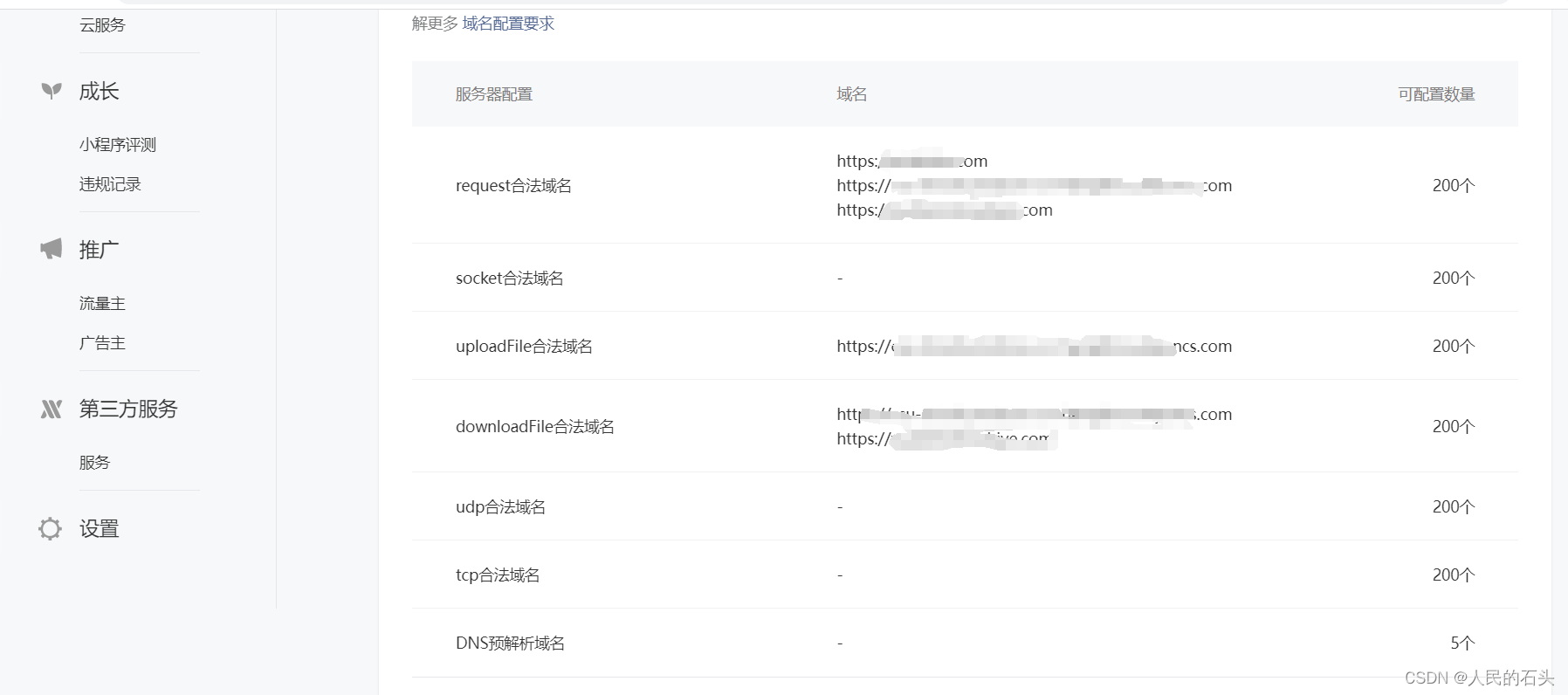
微信小程序实现文章内容详情
方案一、使用微信小程序官方提供的webview 前提已经在微信公众平台开发管理配置好了安全域名即: 方案二、把网页转成pdf直接展示 前提已经在微信公众平台开发管理配置好了安全域名即: 实现思路是发起网络请求拿到pdf下载地址,然后wx.download…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
