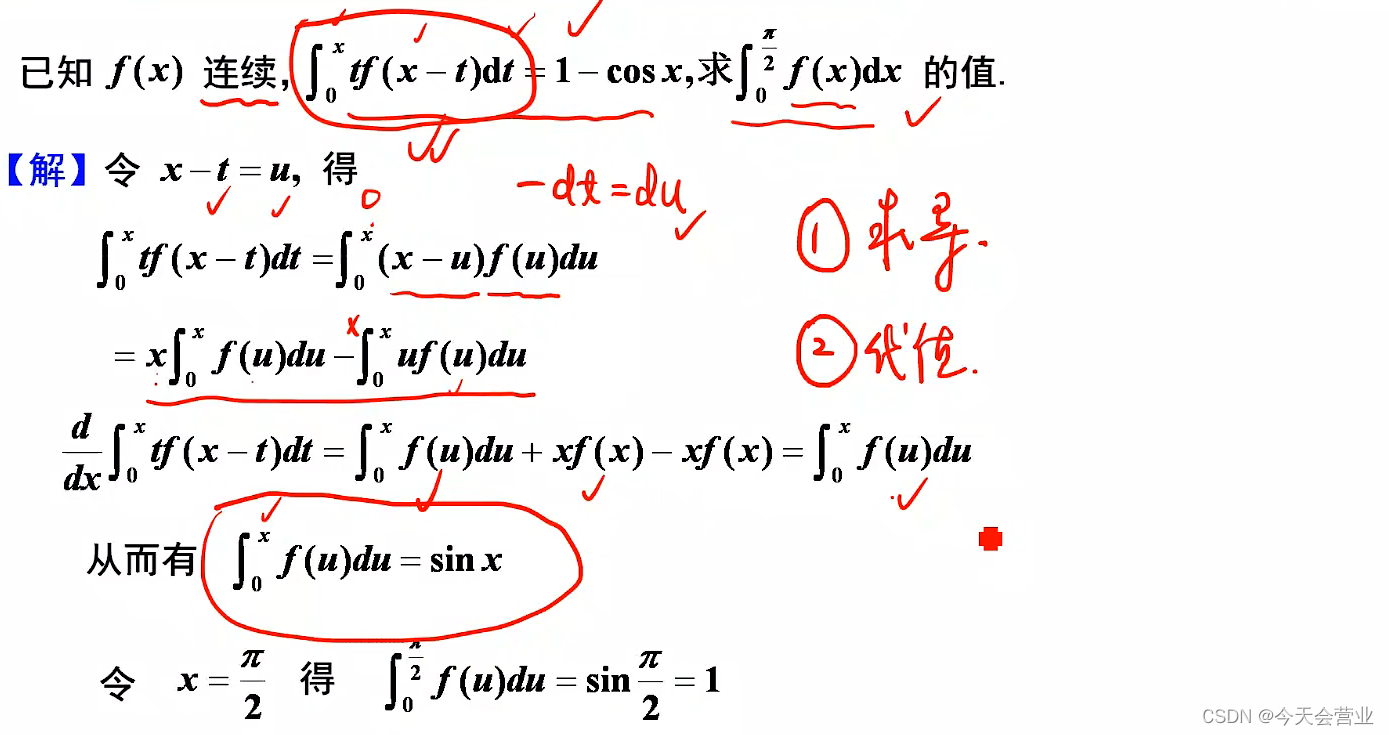数据结构与算法-二叉树的遍历

🌞 “少年没有乌托邦,心向远方自明朗!”
二叉树
- 🎈1.二叉树的遍历
- 🔭1.1先序遍历
- 🔭1.2中序遍历
- 🔭1.3后序遍历
- 🔭1.4层次遍历
- 🔭1.5二叉树遍历的递归算法
- 📝1.5.1先序遍历
- 📝1.5.2中序遍历
- 📝1.5.3后序遍历
- 📝1.5.4例题一
- 📝1.5.5例题二
- 📝1.5.6例题三
- 🔭1.6二叉树遍历的非递归算法
- 🔭1.7例题四
🎈1.二叉树的遍历
二叉树的遍历是按照一定次序访问二叉树中的所有结点,且每个结点仅被访问一次的过程。遍历线性结构是容易解决的,而二叉树的结构是非线性结构,需要寻找规律,使二叉树的结点排列在一个线性队列上,便于遍历。
由二叉树的递归定义知,二叉树有根结点、左子树和右子树3个基本单元组成。如果以L、D、R分别表示遍历左子树、遍历根结点和遍历右子树,则遍历整个二叉树有DLR、LDR、LRD、DRL、RDL、RLD六种遍历方案。若规定先左后右,则只有DLR、LDR、LRD三种遍历方案,分别称为先序遍历、中序遍历和后序遍历。
🔭1.1先序遍历
🔎先序遍历二叉树的过程如下:
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
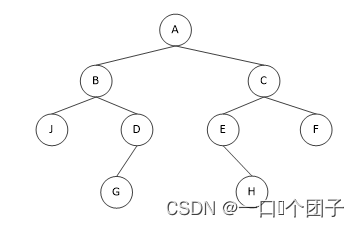
✅ 如下图所示二叉树的先序序列为:ABJDGCEHF

🔭1.2中序遍历
🔎中序遍历二叉树的过程如下:
- 中序遍历左子树
- 访问根结点
- 中序遍历右子树
✅ 如下图所示二叉树的中序序列为:JBGDAEHCF

🔭1.3后序遍历
🔎后序遍历二叉树的过程如下:
- 后序遍历左子树
- 后序遍历右子树
- 访问根结点
✅ 如下图所示二叉树的后序序列为:JGDBHEFCA
🔭1.4层次遍历
🔎二叉树非空(设二叉树的高度为h时),层次遍历二叉树的过程如下:
- 先访问根结点(第1层)
- 再从左向右访问每层结点
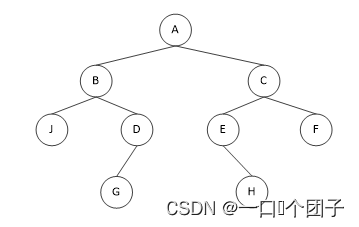
✅ 如下图所示二叉树的层次序列为:ABCJDEFGH
🔭1.5二叉树遍历的递归算法
📝1.5.1先序遍历
void BiTree::InTraverse(BitNode* t)
{//中序遍历递归函数if (t){cout << data;InTraverse(t->lchild);InTraverse(t->rchild);}
}
void BiTree::InTraverseBiTree()
{BitNode* p = bt;InTraverse(p);
}
📝1.5.2中序遍历
void BiTree::InTraverse(BitNode* t)
{//中序遍历递归函数if (t){InTraverse(t->lchild);cout << data;InTraverse(t->rchild);}
}
void BiTree::InTraverseBiTree()
{BitNode* p = bt;InTraverse(p);
}
📝1.5.3后序遍历
void BiTree::InTraverse(BitNode* t)
{//中序遍历递归函数if (t){InTraverse(t->lchild);InTraverse(t->rchild);cout << data;}
}
void BiTree::InTraverseBiTree()
{BitNode* p = bt;InTraverse(p);
}
📝1.5.4例题一
已知二叉树采用二叉链表存储结构存储,设计一个交换二叉树左右子树的递归算法。
void ChangeSubTree(BitNode*& t)
{BitNode* temp;if (t){temp = new BitNode;temp = t->lchild;t->lchild = t->rchild;t->rchild = temp;ChangeSubTree(t->lchild);ChangeSubTree(t->rchild);}
}
📝1.5.5例题二
已知二叉树采用二叉链表结构存储,请设计一个判断两棵二叉树是否相似的算法。若相似返回
1,否则返回0.所谓两棵二叉树s和t相似是指s和t均为空的二叉树;或者s和t的根结点相似(值可以不同),且左右子树分别相似。
int Alike(BitNode* s, BitTree* t)
{if (s == NULL && t == NULL)return 1;else if (s == NULL || t == NULL)return 0;elsereturn Alike(s->lchild, t->lchild) && Alike(s->rchild, t->rchild);
}
📝1.5.6例题三
已知二叉树采用二叉链表存储结构存储,设计一个将二叉树
s拷贝给t的递归算法。
void CopyBitree(BitNode* s, BitNode*& t)
{if (s == NULL)t = NULL;else{t = new BitNode;t->data = s->data;CopyBiTree(s->lchild, t->lchild);CopyBiTree(s->rchild, t->rchild);}
}
🔭1.6二叉树遍历的非递归算法
为了把递归过程改成一个非递归过程,需要利用一个工作栈,记录遍历时的回退路径。
🔎先序遍历的算法流程:
- 用指针
p指向当前需要处理的结点 - 访问该结点,该结点入栈,并将
p指向左孩子,循环处理左子树 - 当该结点无左孩子时,表示栈顶结点无左子树,栈顶结点退栈,并将
p指向刚出栈结点的右孩子 - 对右子树进行相同处理
- 重复上述过程,直到栈为空为止
void PreTraverse(BitNode* t)
{BitNode* p = t;SqStack s;while (p || !s.EmptyStack()){if (p){//访问根结点,根结点指针入栈,遍历左子树cout << p->data;//访问结点s.Push(p);p = p->lchild;}else{//根结点退栈,遍历右子树s.Pop(p);p = p->rchild;}}
}
🔎中序遍历的算法流程:
- 用指针
p指向当前需要处理的结点,p入栈 - 扫描该结点的左子树上的所有结点并将它们一一进栈
- 当该结点无左孩子时,表示栈顶结点无左子树,栈顶结点退栈,该问该结点,并将
p指向刚出栈结点的右孩子 - 对右子树进行相同处理
- 重复上述过程,直到栈为空为止
void PreTraverse(BitNode* t)
{BitNode* p = t;SqStack s;while (p || !s.EmptyStack()){if (p){//根结点入栈,遍历左子树s.Push(p);p = p->lchild;}else{//根结点退栈,访问结点,遍历右子树s.Pop(p);cout << p->data;//访问结点p = p->rchild;}}
}
🔎后序遍历的算法流程:
- 用指针
p指向当前需要处理的结点,并置标志位flag=0(表示第一次入栈),p入栈 - 扫描该结点的左子树上的所有结点并将它们一一进栈
- 当该结点无左孩子时,表示栈顶结点无左子树,栈顶结点退栈,并判断标志位的值,若
flag=0,置flag=1(表示该结点第二次入栈),该问该结点,并将p指向刚出栈结点的右孩子,若flag=1,则访问该结点,置p = NULL. - 对右子树进行相同处理
- 重复上述过程,直到栈为空为止
typedef struct
{BitNode* pointer;int flag;
}BitNodeFlag;
void PostTraverse(BitNode* t)
{BitNodeFlag bf;BitNode* p = t;SqStack s;while (p || !s.EmptyStack()){if (p){bf.pointer = p;bf.flag = 0;s.Push(bf);p = p->lchild;}else{s.Pop(bf);if (bf.flag == 0){bf.uflag = 1;s.Push(bf);p = p->rchild;}else{cout << bf.pointer->data;p = NULL;}}}
}
🔎层次遍历的算法流程:
层次遍历访问完某一层的结点后,再按照它们的访问次序对各结点的左、右子树顺序访问。如此一层一层地访问,先访问的结点其左、右孩子也要先访问。层次遍历过程可以用队列来实现。
void LevelTraverse(BitNode* t)
{BitNode* p = t;LinkQueue q;//初始化建立空队列if (p)q.Enqueue(p);//根结点入队while (!q.EmptyQueue()){q.DeQueue(p);//出队cout << p->data;//访问结点if (p->lchild)q.EnQueue(p->lchild);//左子树根结点入队if (p->rchild)q.EnQueue(p->rchild);//右子树根结点入队}
}
🔭1.7例题四
已知二叉树采用二叉链表存储结构存储,设计一个计算二叉树叶子结点的非递归算法。
int CountBitLeaf(BitNode* t)
{SqStack s;BitNode* p = t;int count = 0;while (p != NULL || !s.EmptyStack()){while (p != NULL){s.Push(p);p = p->lchild;}if (!s.EmptyStack()){s.Pop(p);if (p->lchild == NULL && p->rchild == NULL)count++;p = p->rchild;}}return count;
}
好啦,关于二叉树的遍历的知识到这里就先结束啦,后期会继续更新学习数据结构与算法的相关知识,欢迎大家持续关注、点赞和评论!❤️❤️❤️
相关文章:

数据结构与算法-二叉树的遍历
🌞 “少年没有乌托邦,心向远方自明朗!” 二叉树 🎈1.二叉树的遍历🔭1.1先序遍历🔭1.2中序遍历🔭1.3后序遍历🔭1.4层次遍历🔭1.5二叉树遍历的递归算法📝1.5.1先…...
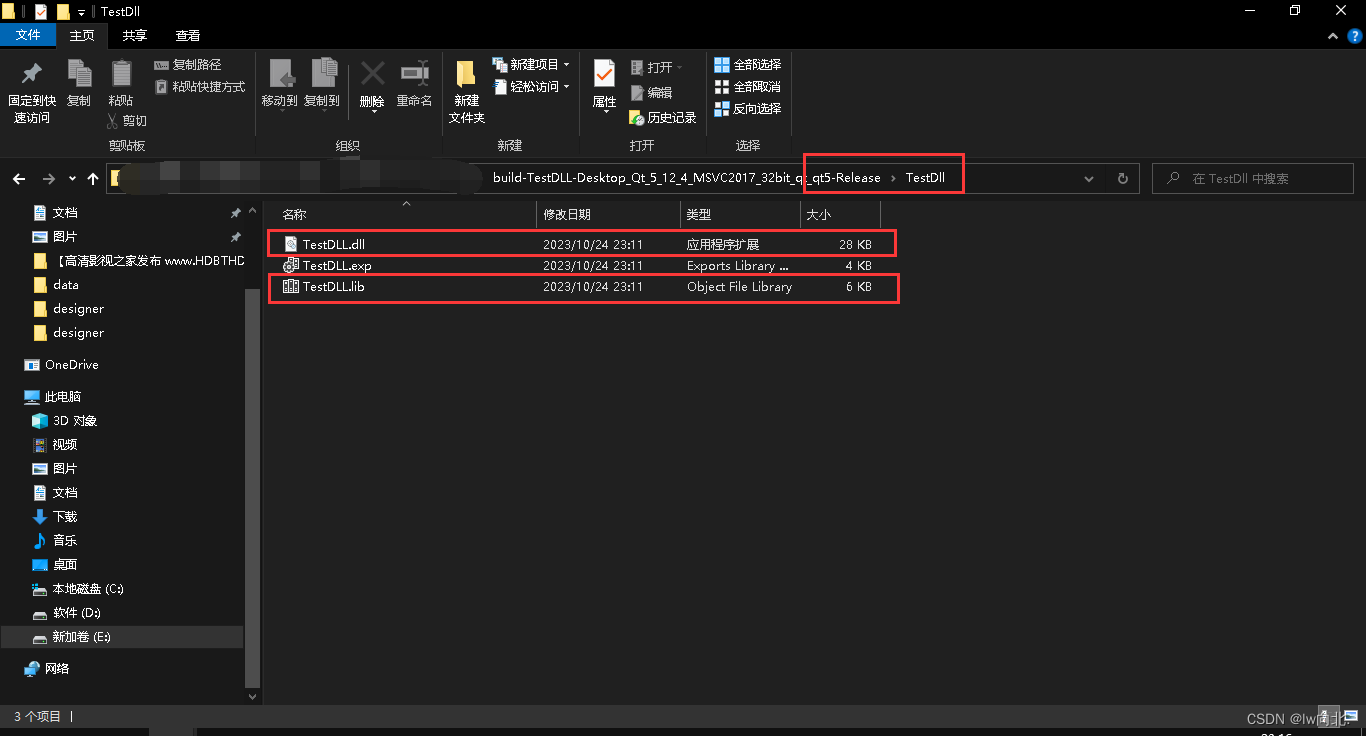
Qt之普通项目如何生成DLL(含源码+注释)
文章目录 一、示例图二、普通项目需要改造的内容三、源码(创建了一个TestDLL的项目,更改内容主要在pro文件和maindow.h文件)TestDLL.promainwindow.hmainwindow.cppmainwindow.ui 总结 一、示例图 使用不同的编译模式编译,会在对…...

Java注解及自定义注解
注解/元数据(Annotation),是对代码级别的说明;在JDK1.5及以后版本引入的一个特性,与类、接口、枚举是在同一个层次。可以声明在包、类、字段、方法、局部变量、方法参数等的前面,用来对这些元素进行说明、注…...

ps2024滤镜插件Portraiture
Photoshop 是最常用到的综合性的设计工具,虽然PS一直在迭代升级,但是在细节功能上,PS总是无法完全满足全部所有的用户需求,今天coco玛奇朵推荐一个个截至目前最受欢迎的免费的PS插件,有了这些功能扩展的插件后PS如虎添…...

Vue 实战项目(智慧商城项目): 完整的订单购物管理功能 内涵资源代码 基于Vant组件库 Vuex态管理 基于企业级项目开发规范
鹏鹏老师的实战开发项目 文章目录 智慧商城项目01. 项目功能演示1.明确功能模块2.项目收获 02. 项目创建目录初始化vue-cli 建项目 03. 调整初始化目录结构1.删除文件2.修改文件3.新增目录 04. vant组件库及Vue周边的其他组件库05. 全部导入和按需导入的区别06. 全部导入07. 按…...

JVM——一些零散的概念(后续学习深入了再补充)
Native 凡是带了native关键字的,说明Java的作用范围的达不到了,需要调用底层C语言的库 调用native方法,会进入本地方法栈,调用本地接口(JNI) JNI的作用:扩展Java的使用,融合不同的编程语言为Java所用 它在内…...

OpenCV学习(三)——响应鼠标事件(获取点击点坐标和颜色,利用鼠标进行绘图)
响应鼠标事件 3. 响应鼠标事件3.1 获取鼠标点击的坐标3.2 获取鼠标点击像素点的颜色3.3 在鼠标点击的位置生成圆3.4 通过拖动鼠标来绘制填充矩形3.5 通过拖动鼠标绘制未填充矩形3.6 使用鼠标选点绘制多边形3.7 按住鼠标左键进行绘图 3. 响应鼠标事件 使用OpenCV读取图像&#…...

基于安卓android微信小程序的投票系统
项目介绍 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,投票系统小程序被用户普遍使用,为方便用户…...

没有上司的舞会
有了上一篇博客,没有看上一篇博客的可以看看上一篇博客,我们对没有上司的舞会这道题会有更好的理解~ 所以关键的思路就是确定对于每一个节点我们应该维护什么内容才是最合适的,这个题目和上一篇博客的最后一道题目很相似,我们思考…...
RHCE8 资料整理(四)
RHCE8 资料整理 第四篇 存储管理第13章 硬盘管理13.1 对磁盘进行分区13.2 交换分区(swap分区) 第14章 文件系统14.1 了解文件系统14.2 了解硬链接14.3 创建文件系统14.4 挂载文件系统14.5 设置永久挂载14.6 查找文件14.7 find的用法 第15章 逻辑卷管理15…...

目标跟踪ZoomTrack: Target-aware Non-uniform Resizing for Efficient Visual Tracking
论文作者:Yutong Kou,Jin Gao,Bing Li,Gang Wang,Weiming Hu,Yizheng Wang,Liang Li 作者单位:CASIA; University of Chinese Academy of Sciences; ShanghaiTech University; Beijing Institute of Basic Medical Sciences; People AI, Inc 论文链接&…...

Flink Data Sink
本专栏案例代码和数据集链接: https://download.csdn.net/download/shangjg03/88477960 1. Data Sinks 在使用 Flink 进行数据处理时,数据经 Data Source 流入,然后通过系列 Transformations 的转化,最终可以通过 Sink 将计算结果进行输出,Flink Data Sinks 就是用于定义…...
机器学习——正则化
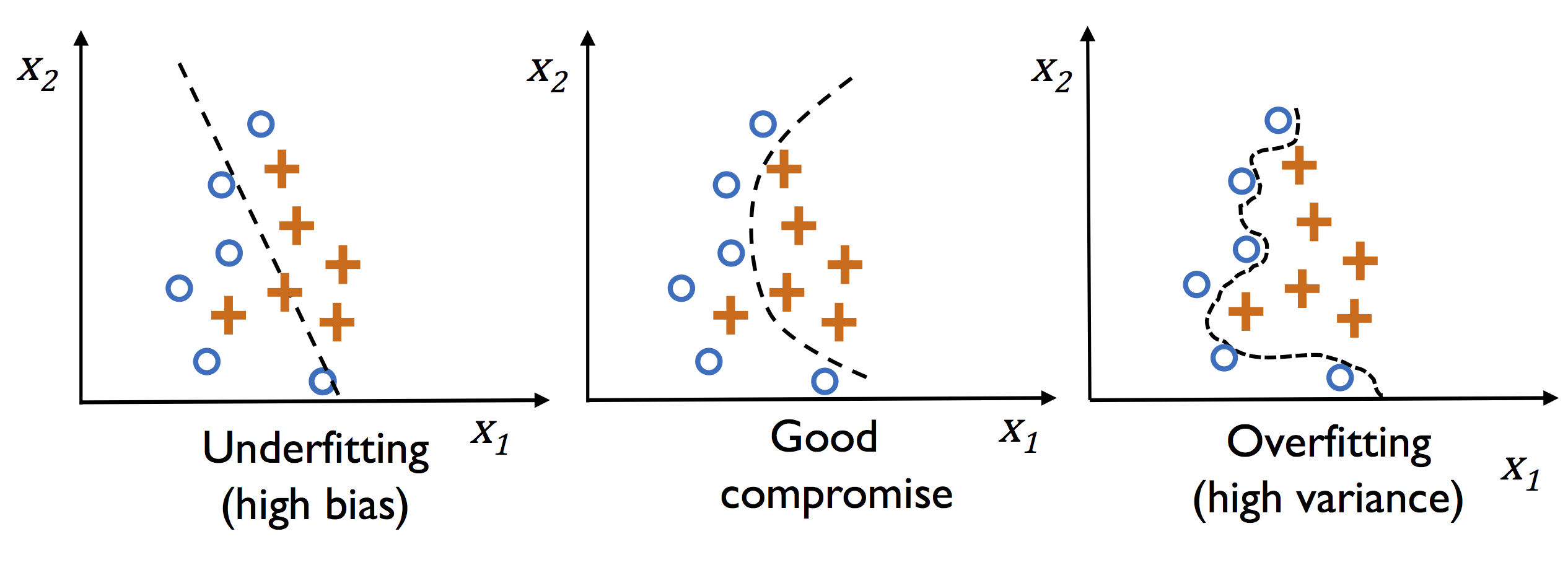
正则化 在机器学习学习中往往不知道需要不知道选取的特征个数,假如特征个数选取过少,容易造成欠拟合,特征个数选取过多,则容易造成过拟合。由此为了保证模型能够很好的拟合样本,同时为了不要出现过拟合现象࿰…...
)
【c++】打家劫舍(动态规划)
打家劫舍 题目难度:高阶 时间限制:1000ms 内存限制:256mb 题目描述 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统ÿ…...

eslint提示 xxx should be listed in the project's dependencies
有时候手动安装了一个npm包A,npm包A里面包含了npm包B,这时候如果 import xxx from npm包B;eslint会报错,提示 npm包B 不在 package.json 里面 解决方法:在 eslintrc.js 增加配置 module.exports {rules: {import/no-extraneous-d…...

H3C LC-5120-52SC-HI配置管理IP
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、MGMT是什么?二、配置步骤1.连接ConsoleWindowsLinux1.配置minicom2.使用minicom 2.配置管理端口3.配置Web管理4.http其它配置项 总结 前言 最近…...
)
数据结构与算法之排序: 归并排序 (Javascript版)
排序 排序:把某个乱序的数组变成升序或降序的数组 (这里用数组来做举例) 归并排序 该排序属于 分治 策略将一个问题分解为两个问题来计算,计算完成之后,就会得到子任务的解,这些解不是最终问题的解,还需要merge起来…...
Java练习题2021-2
"某地大数据防疫平台记录了往来的所有防疫相关信息,包括 本地或外地人员、健康码颜色、接种疫苗情况、最近一次核酸结果、最近一次核酸检测时间等。 该地某区域对于进入人员的要求为: 如果是本地人员,需要绿码和疫苗完全接种方可进入&am…...

深度学习面试题目01
01 什么是神经网络?02 请解释前馈神经网络(Feedforward Neural Network)的工作原理。03 什么是激活函数,为什么它在神经网络中重要?04 请解释反向传播算法(Backpropagation)05 什么是过拟合&…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...