『力扣刷题本』:轮转数组
一、题目
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
二、思路解析
这道题我又是没做出来啦,不过我学到了一个新的解题方法--双数组!
顾名思义,就是利用一个新数组来解题。
这道题里面,我们其实只要想明白一步即可,就是怎么把因为轮转而存不下的元素先给存下来,就行啦。
那么,我们可以用这一步来解决:
newArr[(i + k) % n] = nums[i];把这些元素放好之后,我们在对数组进行一个拷贝即可。这个拷贝的方法,也是我不太熟悉的,嗯,直到自己哪里薄弱,是件好事,以后广而避之就行。
三、完整代码
class Solution {public void rotate(int[] nums, int k) {int[] newArray = new int [nums.length];for(int i = 0; i < nums.length ; i++){newArray[(i+k)%nums.length] = nums[i];}System.arraycopy(newArray,0,nums,0,nums.length);}
}以上就是本篇博客的全部内容啦,如有不足之处,还请各位指出,期待能和各位一起进步!
相关文章:

『力扣刷题本』:轮转数组
一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,…...
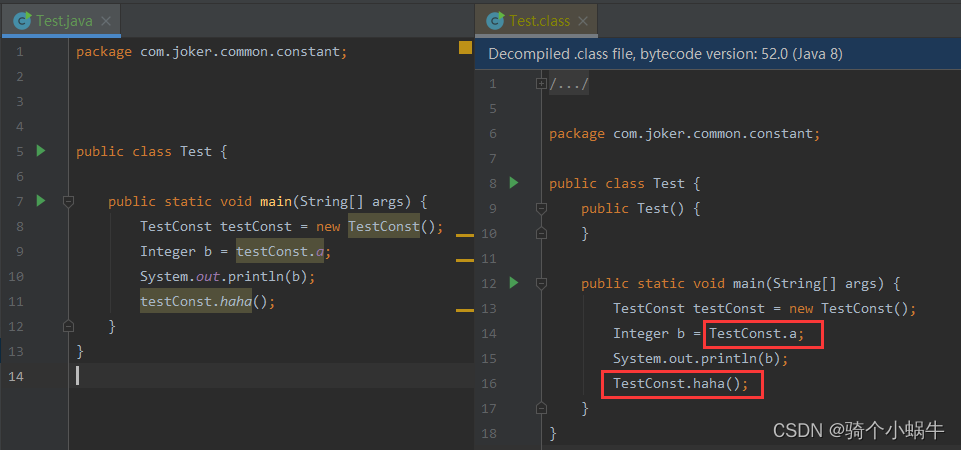
Java关于实例对象调用静态变量和静态方法问题
直接去看原文 原文链接:Java关于实例对象调用静态变量和静态方法问题_java对象可以调用static方法吗_骑个小蜗牛的博客-CSDN博客 --------------------------------------------------------------------------------------------------------------------------------- 实例…...

【开源】基于SpringBoot的海南旅游景点推荐系统的设计和实现
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用户端2.2 管理员端 三、系统展示四、核心代码4.1 随机景点推荐4.2 景点评价4.3 协同推荐算法4.4 网站登录4.5 查询景点美食 五、免责说明 一、摘要 1.1 项目介绍 基于VueSpringBootMySQL的海南旅游推荐系统ÿ…...

字符串中的assert和strcat
assert:函数原型是:void assert( int expression );其作用是现计算表达式 expression ,如果其值为假(即为0),那么它先 stderr 打印一条出信息,然后通过调用 abort 来终止程序运行。使用assert 的缺点是,频繁的调用会影…...
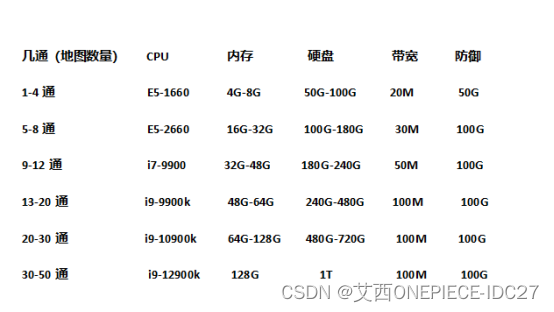
方舟生存进化ARK个人服务器搭建教程保姆级
方舟生存进化ARK个人服务器搭建教程保姆级 大家好我是艾西,在很久之前我有给大家分享过方舟生存进化的搭建架设教程,但时间久远且以前的教程我现在回头看去在某些地方说的并不是那么清楚。最近也是闲暇无事打算重新巩固下方舟生存进化的搭建架设教程&…...

SpringBoot可以连接RabbitMQ集群吗 ?
目录 一、SpringBoot可以连接RabbitMQ集群吗?二、springboot连接到rabbitmq集群可以负载均衡吗?三、SpringBoot既然可以配置负载均衡,为什么还需要Haproxy做负载均衡? 一、SpringBoot可以连接RabbitMQ集群吗? Spring …...

【机器学习】KNN算法-模型选择与调优
KNN算法-模型选择与调优 文章目录 KNN算法-模型选择与调优1. 交叉验证2. 超参数搜索-网格搜索(Grid Search)3. 模型选择与调优API4. 鸢尾花种类预测-代码和输出结果5. 计算距离 问题背景:KNN算法的K值不好确定 1. 交叉验证 交叉验证&#x…...

NPM【问题 01】npm i node-sass@4.14.1报错not found: python2及Cannot download问题处理
node-sass安装问题处理 1.问题2.处理2.1 方案一【我的环境失败】2.2 方案二【成功】2.3 方案三【成功】 1.问题 gyp verb which failed Error: not found: python2 # 1.添加Python27的安装路径到环境变量 gyp verb check python checking for Python executable "python…...

redis集群中节点fail,noaddr
文章目录 1. 问题:fail,noaddr2. cluster nodes节点信息解读2.1 每个字段的含义2.2 flags字段各标记含义 3. redis集群fail,noaddr问题解决4. cluster指令5. 相关文章(1) redis集群搭建(2) 华为云两台机器内网互联(3) /etc/rc.d/init.d 详解|程序开机自启(4) Redis5…...
Fourier分析导论——第1章——Fourier分析的起源(E.M. Stein R. Shakarchi)
第 1 章 Fourier分析的起源 (The Genesis of Fourier Analysis) Regarding the researches of dAlembert and Euler could one not add that if they knew this expansion, they made but a very imperfect use of it. They were both persuaded that an arbitrary and d…...
使用Node.js软件包管理器(npm)安装TypeScript
安装node.js node.js的安装很简单,这里不再赘述,如果大家有需要,可以看一下这个:https://blog.csdn.net/David_house/article/details/123218488 检验电脑上node.js是否安装成功,或者是否已经安装node.js,…...
鸿蒙ArkUI-X跨端应用开发,一套代码构建多平台应用
文章目录 一、项目介绍二、技术架构三、Gitee仓库地址四、ArkUI-X开发者文档五、快速开始——环境准备1、下载DevEco Studio,版本V4.0 Beta2以上2、打开DevEco,下载相关环境配置3、配置开发环境3.1、OpenHarmony SDK3.2、安装ArkUI-X SDK3.2、Android SD…...

【鸿蒙软件开发】ArkTS基础组件之Gauge(环形图表)、LoadingProgress(动态加载)
文章目录 前言一、Gauge环形图表1.1 子组件1.2 接口参数介绍 1.2 属性1.3 示例代码二、LoadingProgress2.1 子组件2.2 接口2.3 属性2.4 示例代码 总结 前言 Gauge:数据量规图表组件,用于将数据展示为环形图表。 LoadingProgress:用于显示加载…...
C++模板类用作参数传递
前言 在模板类<>传递参数的一种实现。记不住,以此记录。 // dome.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 // #define _CRT_SECURE_NO_WARNINGS #include <iostream> //#include "tools.h" #include <fu…...
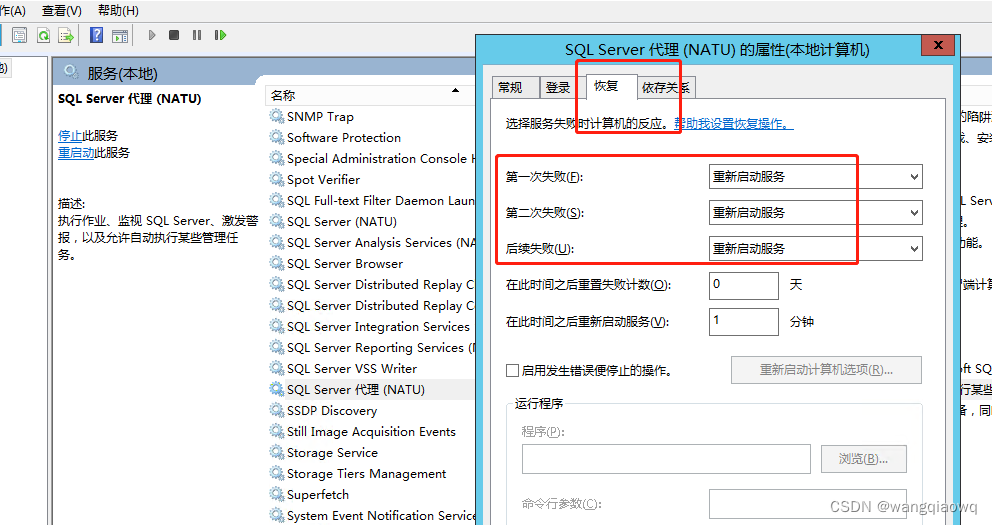
SQL server 代理服务启动和查看
设置重启 使用管理员权限登录到运行 SQL Server 代理服务的计算机。 打开 Windows 服务管理器。可以通过按下 Windows 键 R,然后键入 "services.msc" 并按 Enter 来打开服务管理器。 在服务列表中,找到 "SQL Server Agent" 服务&…...

单例模式详解【2023年最新】
一、单例模式概念 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来访问该实例。它的目的是限制一个类只能创建一个对象,以确保在整个应用程序中只有一个共享的实例。 单例模式通常用于以下情况:…...
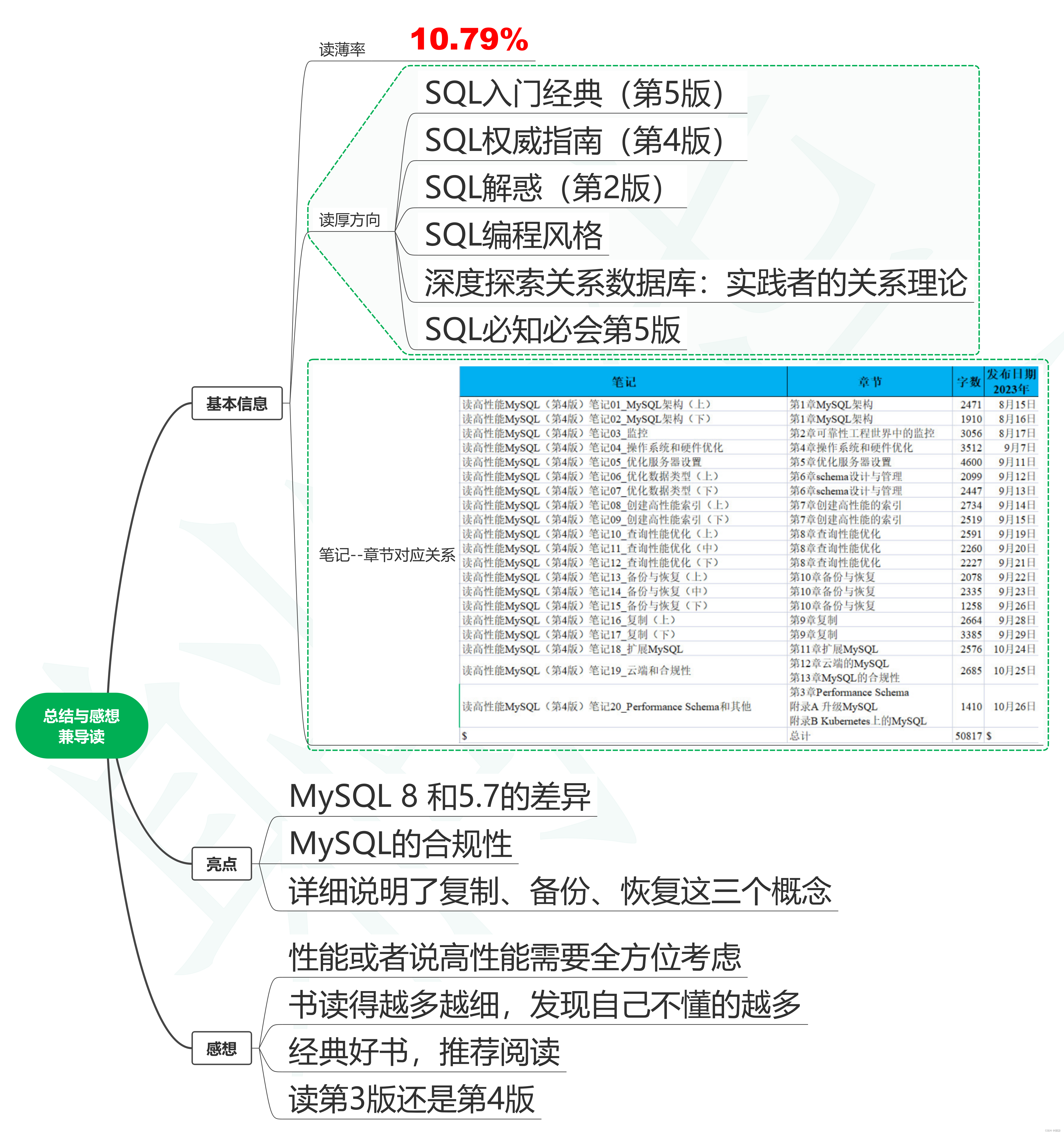
读高性能MySQL(第4版)笔记21_读后总结与感想兼导读
1. 基本信息 高性能MySQL:经过大规模运维验证的策略(第4版) High Performance MySQL, Fourth Edition [美] Silvia Botros(西尔维亚博特罗斯);Jeremy Tinley(杰里米廷利) 电子工业出版社,2022年10月出版 1.1. 读薄率 书籍总字…...

放学辣[简单版]
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 本题和 D 题的唯一区别是 NNN 的范围。 校园里目前有 NNN 名学生,这些学生属于 MMM 个班级。第 iii(i1,2,...,Ni 1,2,...,Ni1,2,...,N)个人属于第…...

面向对象设计——原型模式
原型设计模式是一种创建型设计模式,其主要目标是创建对象的新实例,同时尽量减少与使用者的交互,以降低对象创建的复杂性。这通过复制(或克隆)现有对象的实例来实现,以获得新对象,而不是通过实例化类来创建。 以下是原型设计模式的关键概念: 原型接口(Prototype Inter…...
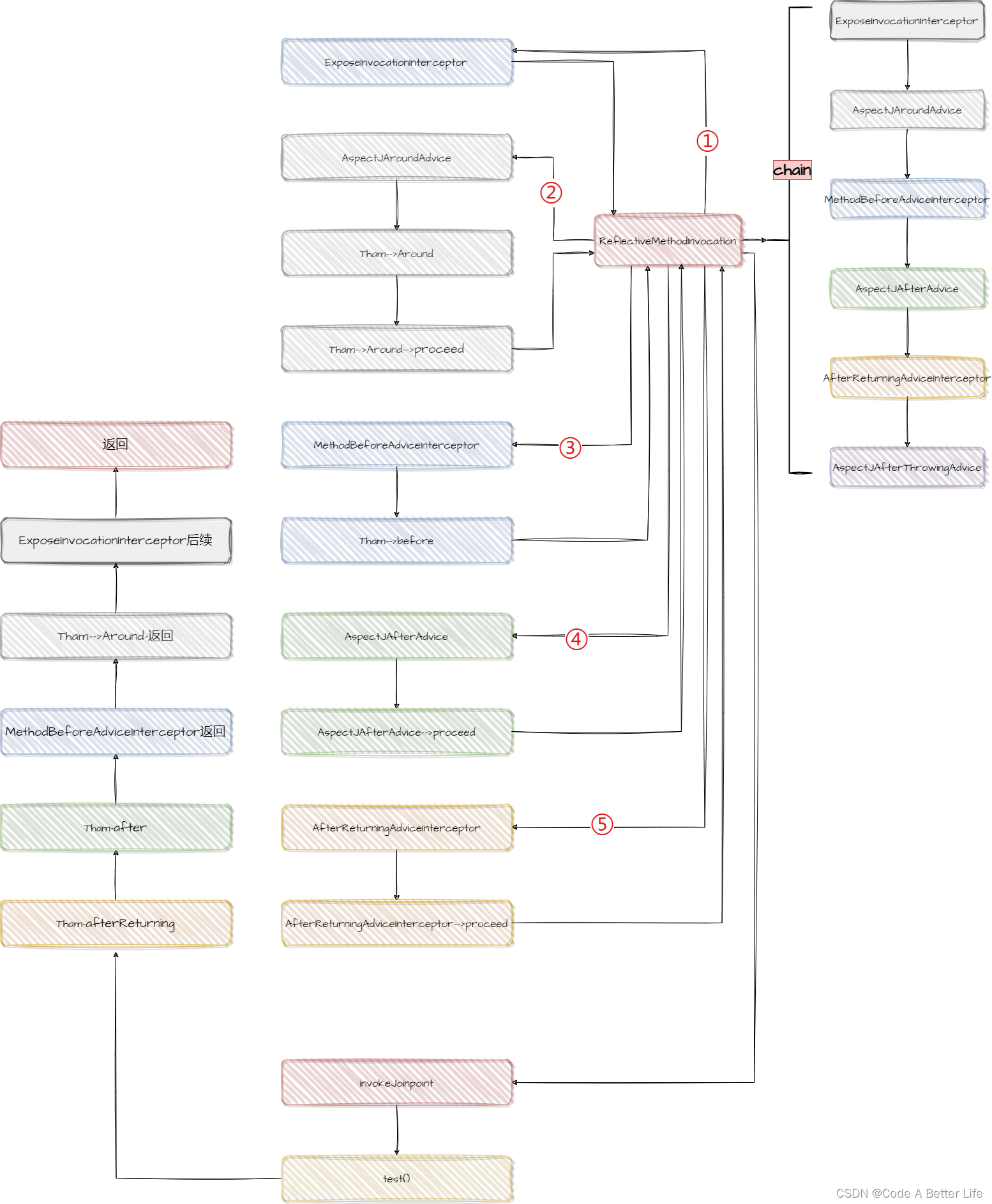
SpringAOP源码解析之advice执行顺序(三)
上一章我们分析了Aspect中advice的排序为Around.class, Before.class, After.class, AfterReturning.class, AfterThrowing.class,然后advice真正的执行顺序是什么?多个Aspect之间的执行顺序又是什么?就是我们本章探讨的问题。 准备工作 既…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
