文件权限详解
一、文件类型
ll指令查看文件详细信息中,第一列就是文件类型。
常见的文件类型有:
1、 - :普通文件 (文本、源代码、图片、视频、可执行)
2、 d :目录文件
3、b :块设备
4、c :字符设备
5、l:链接文件
6、p:管道文件
7、s:socket文件
二、文件的权限
文件权限分为:读(r),写(w),执行(x)。
对于文件而言,用户也分为三类:拥有者(user),所属组(group),其他(other)。

这里三三为一组,顺序为:user、group、other
为 '-' 则代表没有对应权限,例如 test.txt 的user没有执行权限,other没有写和执行权限。
三、改变文件权限
1、普通文件的权限
1、用 chmod u+r 文件名 给 文件拥有者加读权限
类似操作:chmod u+rw 文件名 chmod g+rx 文件名 chmod o+xw 文件名
拥有者加读写权限 所属组加写执行权限 其他加写执行权限
任意组合即可实现权限的增加和移除。
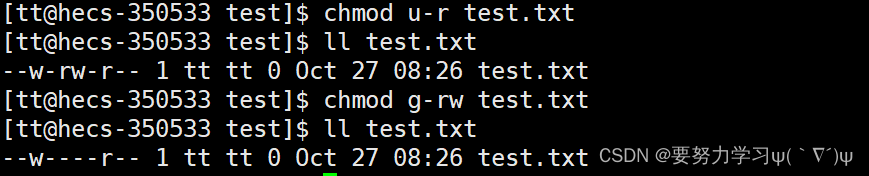
2、因为权限只有 有 和 没有 两个状态,所以可以用1和0标识
因为有三种权限所以三种用户的权限可以用三个八进制表示
777(111111111) 代表 rwxrwxrwx 664(110110100) 代表 rw-rw-r--
所以可以 chmod 777 文件名 添加所有权限给全部人

只有文件的拥有者和root可以改变文件的权限!
2、目录文件的权限
对于一个目录而言
r权限代表可否查看目录内文件的信息
w权限代表可否增加和删除文件
x权限代表可否进入目录
没有读权限代表无法看目录内文件的信息!
 没有写权限代表不能在目录中增加和删除文件
没有写权限代表不能在目录中增加和删除文件
 没有执行权限代表无法进入目录
没有执行权限代表无法进入目录

四、umask权限掩码
权限掩码可以用来设置文件的初始权限。
使用方法:umask 0xxx xxx代表三个八进制数字,含义与上面一样
出现在掩码中的权限不会出现在文件的初始权限中
最终权限 = 起始权限 & (~umask) ==> ~umask的意思是对umask按位取反
普通文件的起始权限是666; 目录是777;
起始权限:把umask设为0即可看到
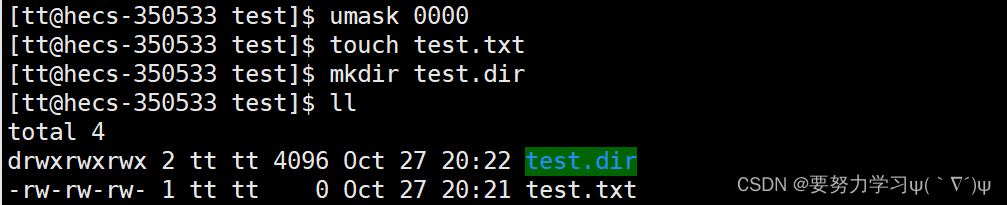
把umask设为0002,所有创建的文件other就没有写权限了
五、粘滞位
在同一台云服务器中,我们无法进入其他用户的目录(root除外),那我们想和别人一起维护一个文件时应该怎么办呢?
在/目录下就存在了tmp目录,文件写在里面,帮助我们不同的用户一起维护同一个文件。
因为tmp目录权限是777,所以我们写在里面的文件是可以被其他无关用户删掉的!!
为了解决这个问题,就引入了粘滞位,把目录的最后一位变成 t ,这样除了拥有者和root之外的其他人就无法删除文件了。
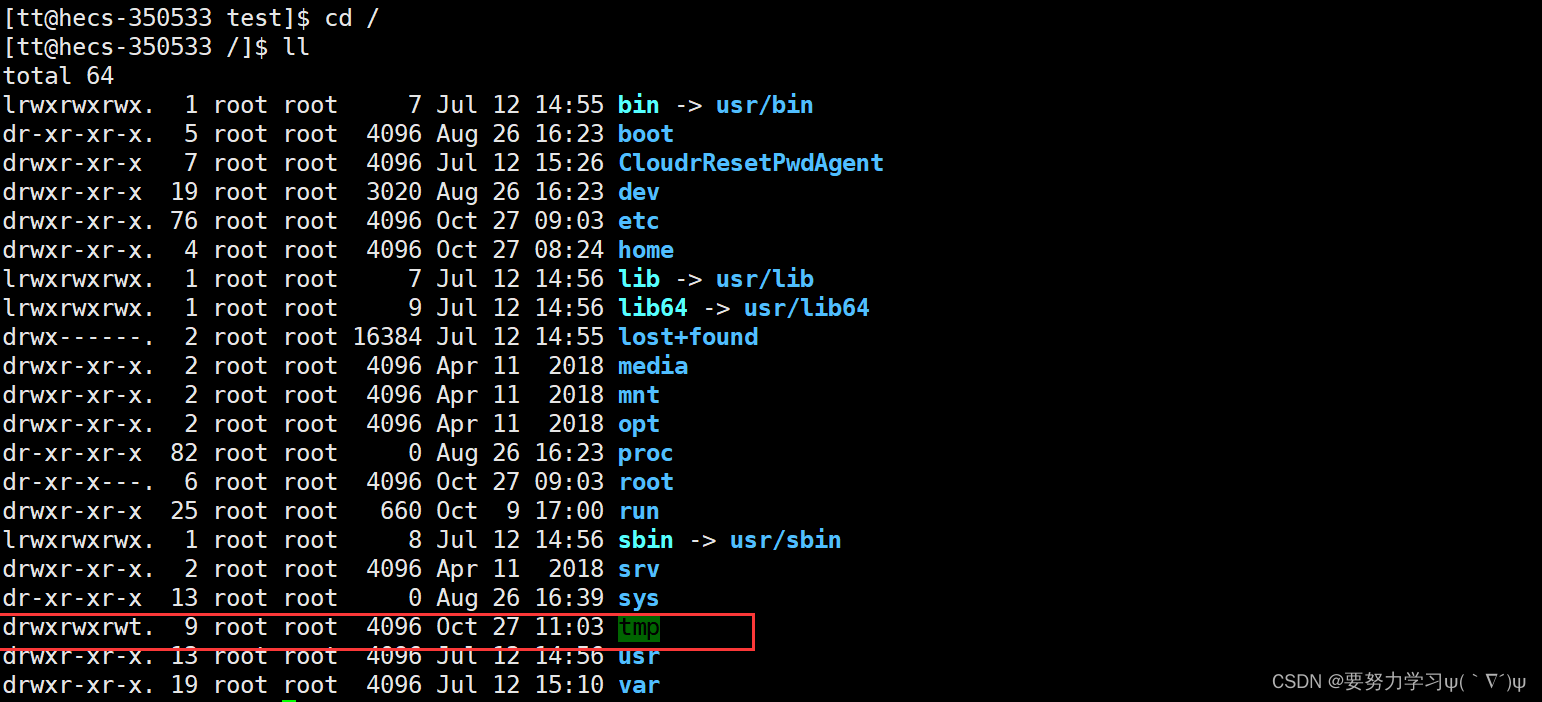
tmp目录最后一位为t,就是粘滞位,让除了文件拥有者、目录拥有者和root之外的其他人就无法删除文件。
我们也可以用chmod 为想要的目录加粘滞位
 感谢大家观看!
感谢大家观看!
相关文章:

文件权限详解
一、文件类型 ll指令查看文件详细信息中,第一列就是文件类型。 常见的文件类型有: 1、 - :普通文件 (文本、源代码、图片、视频、可执行) 2、 d :目录文件 3、b :块设备 4、c ࿱…...

在声明和定义的一些小坑
1、静态成员变量的初始化 静态成员变量声明在 .h 头文件文件中,初始化应该在 .cpp 源文件中 就会出现"找到一个或多个多重定义的符号",下面的错误 class MyString{public:typedef char* iterator;typedef const char* const_iterator;iterator begin();…...
浏览器事件循环 (event loop)
进程与线程 进程 进程的概念 进程是操作系统中的一个程序或者一个程序的一次执行过程,是一个动态的概念,是程序在执行过程中分配和管理资源的基本单位,是操作系统结构的基础。 简单的来说,就是一个程序运行开辟的一块内存空间&a…...
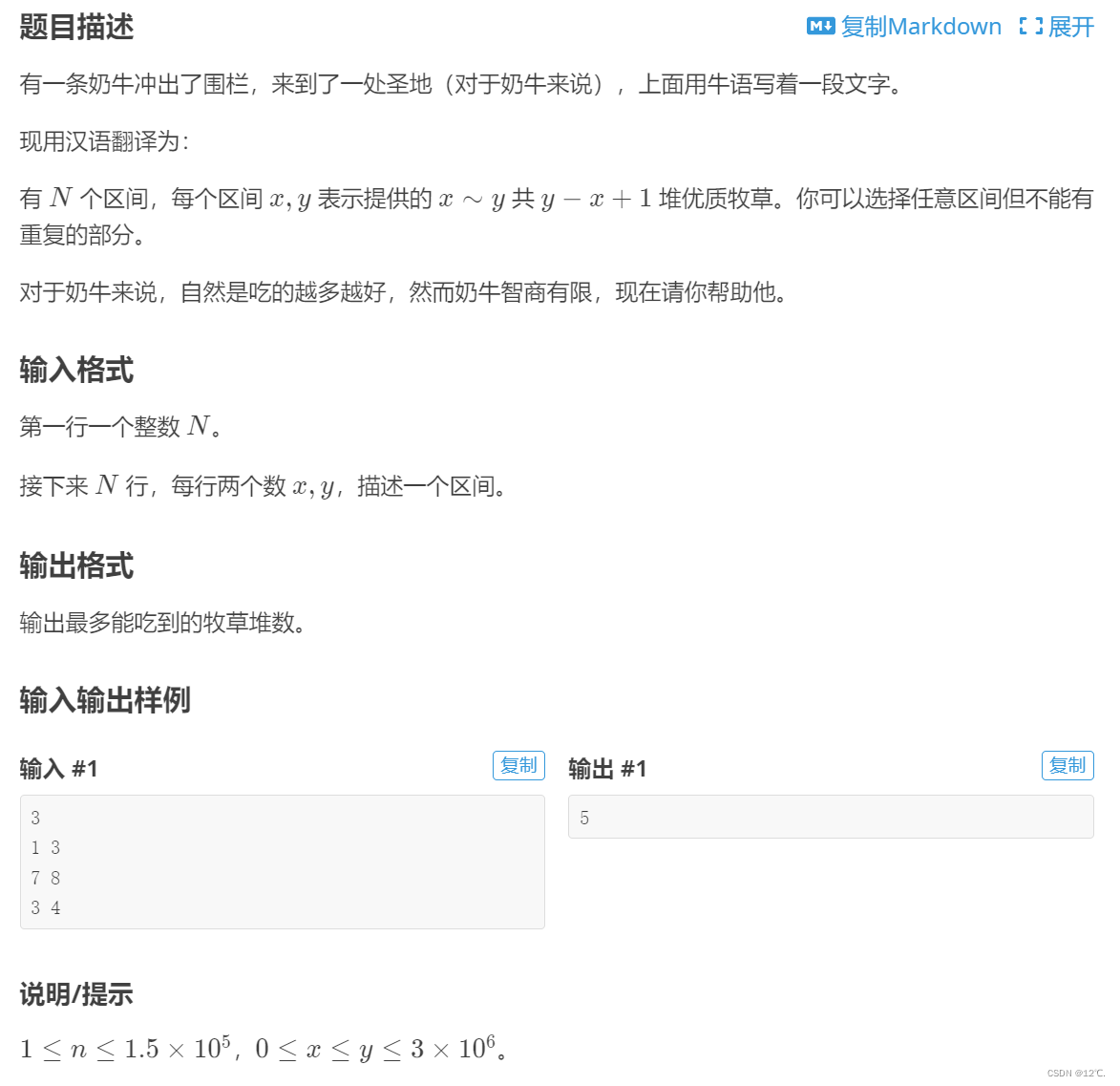
P1868 饥饿的奶牛
根据题意可以知道是一个动态规划,看完数据范围之后可以知道是一个线性DP。 解决方法有点类似于背包问题,枚举背包的每一个空间。 如果把坐标轴上每个点都看成一个块儿,只需要按顺序求出前 i 个块儿的最大牧草堆数,f[i] 就是前i的…...
【软考系统架构设计师】2021年系统架构师综合知识真题及解析
本文主要分享2021年下半年系统架构师综合知识历年真题以及本人在做题时的所思所想。题目序号有点混乱,可忽略 【01】.某计算机系统页面大小为4K,进程P1的页面变换表如下图所示,看P1要访问数据的逻辑地址为十六进制1B1AH,那么该逻辑地址经过变…...
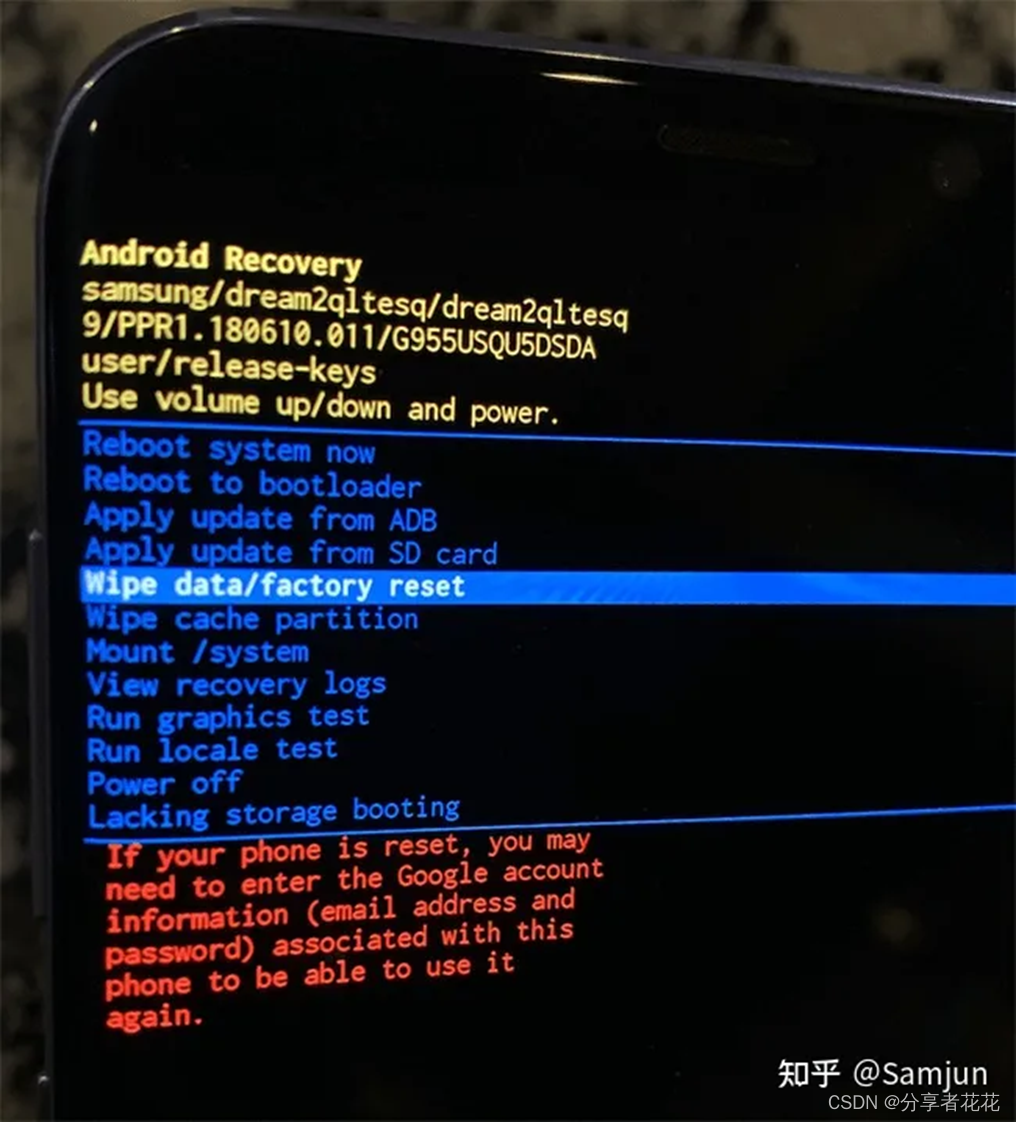
如何在忘记手机密码或图案时重置 Android 手机?
忘记手机密码或图案是 Android 用户一生中不得不面对的最令人沮丧的事情之一。恢复 Android 设备的唯一方法是在 Android 设备上恢复出厂设置。但许多用户不使用此方法,因为此过程会擦除您设备上可用的所有个人数据。 但是,有一种方法可以在不丢失任何数…...

LeetCode每日一题——2520. Count the Digits That Divide a Number
文章目录 一、题目二、题解 一、题目 2520. Count the Digits That Divide a Number Given an integer num, return the number of digits in num that divide num. An integer val divides nums if nums % val 0. Example 1: Input: num 7 Output: 1 Explanation: 7 di…...

论文阅读——DistilBERT
ArXiv:https://arxiv.org/abs/1910.01108 Train Loss: DistilBERT: DistilBERT具有与BERT相同的一般结构,层数减少2倍,移除token类型嵌入和pooler。从老师那里取一层来初始化学生。 The token-type embeddings and the pooler a…...

202212 青少年等级考试机器人实操真题三级
202212 青少年等级考试机器人实操真题三级 考试时间:60分钟 总分:100 及格分:60 一、问答题 (共1题,每题100分) 1、实际操作(共1题,共100分) 请考生在实操考试结束前将本题作答程序文件按“说明”要求完成上传。 1. 主…...
token正确不报错,token失效后却出现报跨域错误
1.今天在使用koajs开发项目时,突然发现前端配置axios的response获取不到后端定义的token失效内容了,取而代之的是出现了跨域的错误。 2. 我马上去查找koajs的跨域中间件配置,发现配置完好cors,token正确时,接口正常访问…...

STM32中除零运算,为何程序不崩溃?
在 C 语言中,除零运算会导致异常吗? 在 C 语言中,当一个数除以零时,会导致除法运算错误,通常表现为“除以零”错误或被称为“浮点异常”(floating-point exception)。 对于整数除法,…...

sprinbboot 2.7启动不生成日志文件
新增了一个springboot项目,通过idea 调试,并且在idea 的vm options中指定-Dlogging.configclasspath:logback-pro.xml 或者 -Dlogging.configclasspath:logback-dev.xml 都能正常生成对应的日志文件。 部署到测试环境以及生产环境,日志文件却…...

Kafka - 3.x 图解Broker总体工作流程
文章目录 Zk中存储的kafka的信息Kafka Broker总体工作流程1. broker启动后向zk中注册2. Controller谁先启动注册,谁说了算3. 由选举出来的Controller监听brokers节点的变化4. Controller决定leader选举5. Controller将节点信息上传到Zk中6. 其他Controller从zk中同步…...

APP自动化测试 ---- Appium介绍及运行原理
在面试APP自动化时,有的面试官可能会问Appium的运行原理,以下介绍Appium运行原理。 一、Appium介绍 1.Appium概念 Appium是一个开源测试自动化框架,可用于原生,混合和移动Web应用程序测试。它使用WebDriver协议驱动IOS…...

学习模板发布
学习目标: 提示:这里可以添加学习目标 例如: 一周掌握 Java 入门知识 学习内容: 提示:这里可以添加要学的内容 例如: 搭建 Java 开发环境掌握 Java 基本语法掌握条件语句掌握循环语句 学习时间&#x…...

Hive 视图和索引
1.视图 1.1 简介 Hive 中的视图和 RDBMS 中视图的概念一致,都是一组数据的逻辑表示,本质上就是一条 SELECT 语句的结果集。视图是纯粹的逻辑对象,没有关联的存储 (Hive 3.0.0 引入的物化视图除外),当查询引用视图时,Hive 可以将视图的定义与查询结合起来,例如将查询中的过…...
EtherCAT主站SOEM-- 0 SOEM下载编译及文件功能介绍
0 介绍EtherCAT主站SOEM文件及主要功能函数 1. soem介绍:2 soem主要功能文件说明:3 soem下载链接4 编译soem4.1 Windows (Visual Studio):4.2 Linux & macOS: 该文档修改记录:总结 1. soem介绍: SOEM&…...

【Python机器学习】零基础掌握RFE特征选择
如何在数据分析中选出关键特征? 面对大量、高维度的数据,如何有效地选取关键特征以提高模型效率和准确度?这是数据分析领域中常见的问题。解决这个问题的一种方法就是递归特征消除(RFE)算法。 假设一个房地产公司希望预测房价,他们收集了很多关于房子的信息,如面积、房…...
R语言的极值统计学、分位数回归、机器学习方法
受到气候变化、温室效应以及人类活动等因素的影响,自然界中极端高温、极端环境污染、大洪水和大暴雨等现象的发生日益频繁;在人类社会中,股市崩溃、金融危机等极端情况也时有发生;今年的新冠疫情就是非常典型的极端现象。研究此类…...
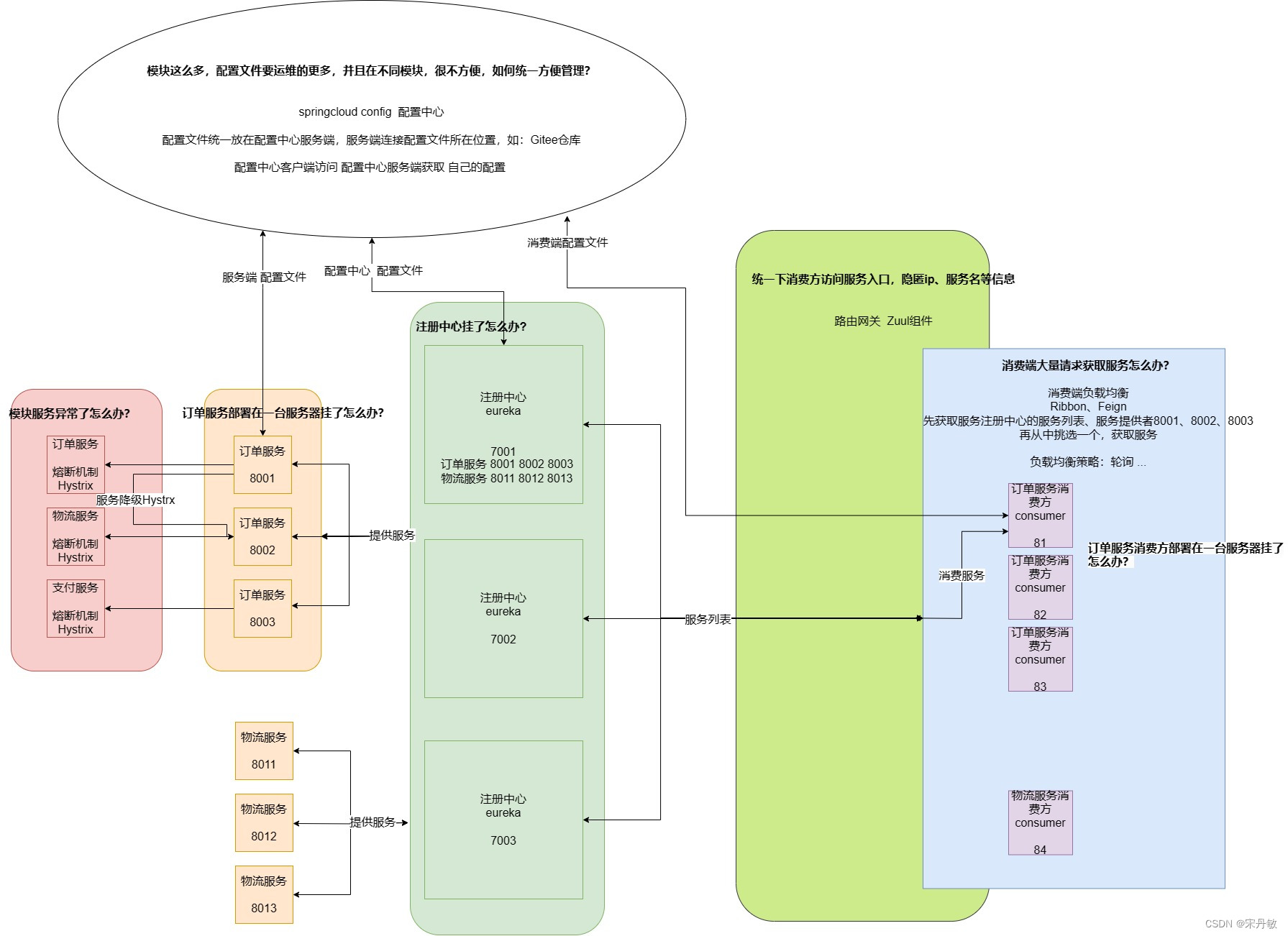
【SpringCloudNetflix】一图理解Spring Cloud Netflix解决了那些微服务问题?
什么是微服务理解: SpringCloudNetflix解决的问题理解: SpringCloudNetflix核心点: 注册中心:Eureka负载均衡:Ribbon、Feign服务熔断:Hystrix服务降级:Hystrix服务监控:Hystrix Da…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...


