软考系统架构师知识点集锦四:信息安全技术基础知识
一、考情分析
二、考点精讲
2.1信息加解密技术
2.1.1对称加密
概念:对称加密(又称为私人密钥加密/共享密钥加密) : 加密与解密使用同一密钥。
特点:加密强度不高,但效率高;密钥分发困难。
(大量明文为了保证加密效率一般使用对称加密)
常见对称密钥加密算法:
DES:替换+移位、56 位密钥、64 位数据块、速度快、密钥易产生
3DES (三重DES) :两个56位的密钥K1、K2
- 加密: K1加密~>K2解密->K1加密
- 解密: K1解密->K2加密->K1解密
IDEA: 128位密钥、64位数据块、比DES的加密性好、对计算机功能要求相对低,PGP。
RC-5算法: RSA数据安全公司的很多产品都使用了RC-5。
AES算法:高级加密标准,又称Rijndael加密法,是美国政府采用的一种区块加密标准。
2.1.2非对称加密
概念:非对称加密(又称为公开密钥加密) :密钥必须成对使用(公钥加密,相应的私钥解密)
特点:加密速度慢,但强度高。秘钥分发容易。
常见非对称密钥加密算法
RSA: 2048位(或1024位)密钥、计算量极大、难破解
ECC-椭圆曲线算法
Elgamal:安全性依赖于计算有限域上离散对数这一难题。
2.2密钥管理技术
2.2.1数字证书
数字证书内容
- 证书的版本信息;
- 证书的序列号,每个证书都有-个唯一的证书序列号;
- 证书所使用的签名算法;
- 证书的发行机构名称,命名规则一般采用X.500格式;
- 证书的有效期,现在通用的证书-般采用UTC时间格式,它的计时范围为1950-2049;
- 证书所有人的名称,命名规则一般采用X.500格式;
- 证书所有人的公开密钥;
- 证书发行者对证书的签名。
2.2.2公钥体系
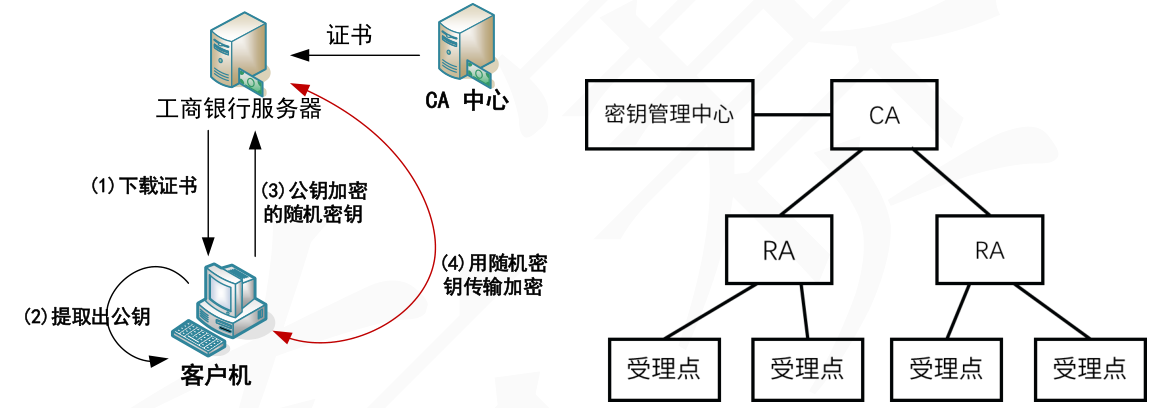
CA (Certificate Authority)认证中心
RA (Registration Authority)注册审批机构
证书受理点
密钥管理中心-KMC
2.3访问控制技术与数字签名
2.3.1访问控制技术
(1)访问控制的基本模型
访问控制的目标有两个:
- 防止非法用户进入系统;
- 阻止合法用户对系统资源的非法使用,即禁止合法用户的越权访问。
访问控制的三要素:
- 主体:可以对其他实体施加动作的主动实体,记为S;
- 客体:是接受其他实体访问的被动实体,记为O;
- 控制策略:是主体对客体的操作行为集和约束条件集,记为KS。
(2)访问控制的实现技术
访问控制矩阵(ACM) :矩阵中的每一格表示所在行的主体对所 在列的客体的访问授权。

访问控制列表:访问控制矩阵按列分解,具体如下: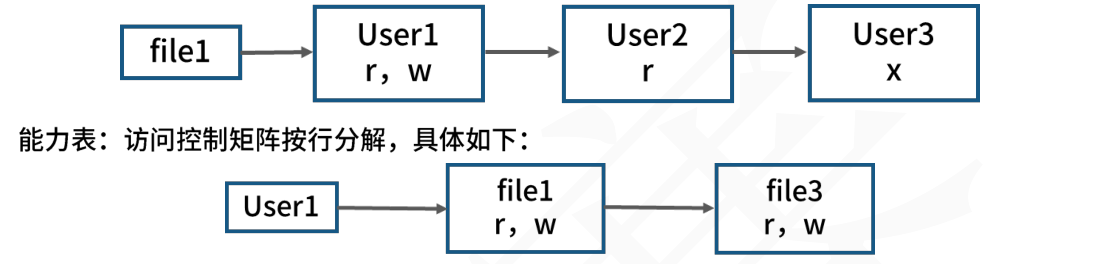
授权关系表:对应访问矩阵中每一个非空元素的实现技术。 例如安全数据库系统通常用授权关系表来实现其访问控制安全机制。
2.3.2数字签名技术
(1)信息摘要:单向散列函数[不可逆]、固定长度的散列值。
摘要用途:确保信息[完整性],防篡改。
常用的消息摘要算法有MD5, SHA等,市场上广泛使用的MD5, SHA算法的散列值分别为128和160位,由于SHA通常采用的密钥长度较长,因此安全性高于MD5。
(2)数字签名的过程如下图所示(发送者使用自己的私钥对摘要签名,接收者利用发送者的公钥对
接收到的摘要进行验证) :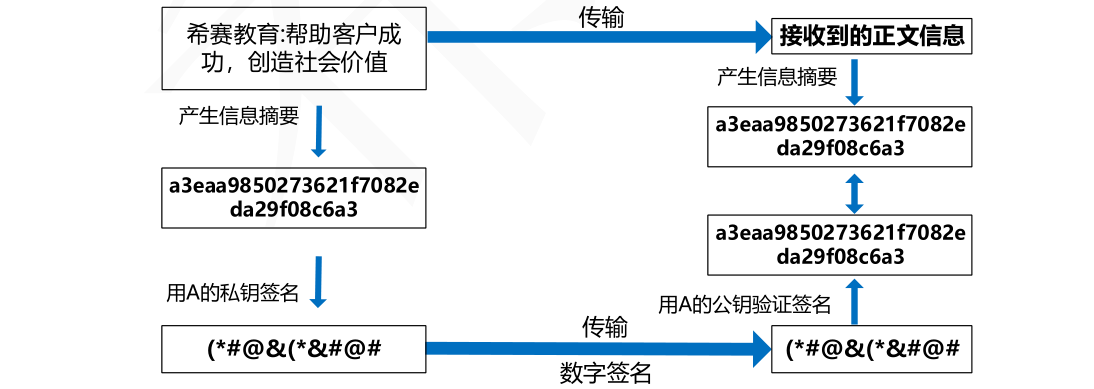
2.4安全架构概述
(1) 信息安全面临的威胁
(2)被动攻击:收集信息为主,破坏保密性。
(3)主动攻击:主动攻击的类别主要有:中断(破坏可用性),篡改(破坏完整性) , 伪造(破坏真实性)。
2.5安全模型
分类: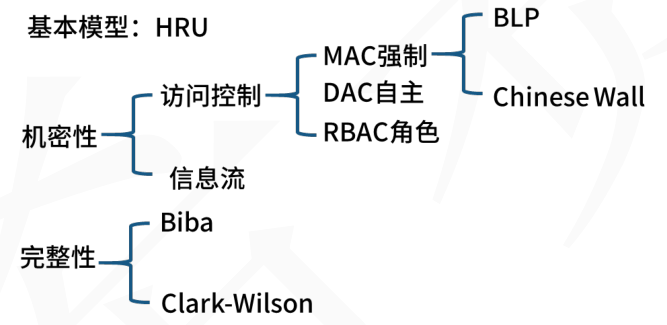
(1)BLP模型
Bell-LaPadula模型是符合军事安全策略的计算机安全模型,简称BLP模型。BLP模型的安全规则如下:
- 简单安全规则:安全级别低的主体不能读安全级别高的客体;
- 星属性安全规则:安全级别高的主体不能往低级别的客体写;
- 强星属性安全规则:不允许对另一级别进行读写;
- 自主安全规则:使用访问控制矩阵来定义说明自由存取控制。
(2) Biba 模型
BiBa模型主要用于防止非授权修改系统信息,以保护系统的信息完整性。该模型同BLP模型类似,采用主体、客体、完整性级别描述安全策略要求。BiBa 模型能够防止数据从低完整性级别流向高完整性级别,其安全规则如下:
- 星完整性规则:表示完整性级别低的主体不能对完整性级别高的客体写数据;
- 简单完整性规则:表示完整性级别高的主体不能从完整性级别低的客体读取数据;
- 调用属性规则:表示一个完整性级别低的主体不能从完整性级别高的客体调用程序或服务。
(3) Chinese Wall模型
Chinese Wall模型的安全策略的基础是客户访问的信息不会与当前他们可支配的信息产生冲突。
其访问客体控制的安全规则如下:
- 与主体曾经访问过的信息属于同一公司数据集合的信息,即墙内信息可以访问;
- 属于一个完全不同的利益冲突组的可以访问;
主体能够对一个客体进行写的前提是主体未对任何属于其他公司数据集进行过访问。
定理1: 一个主体一旦访问过一个客体,则该主体只能访问位于同一公司数据集的客体或在不同利益组的客体。
定理2:在一个利益冲突组中,一个主体最多只能访问一个公司数据集。
2.6区块链技术
(1) [区块链] ≠比特币,比特币底层采用了区块链技术。比特币交易在我国定性为[非法运用]。
(2)区块链的特点:
- 去中心化:由于使用分布式核算和存储,不存在中心化的硬件或管理机构,任意节点的权利和义务都是均等的,系统中的数据块由整个系统中具有维护功能的节点来共同维护。
- 开放性:系统是开放的,如:区块链.上的[交易信息是公开的],不过[账户身份信息是高度加密的]。
- 自治性:区块链采用基于协商- -致的规范和协议 (比如一套公开透明的算法)使得整个系统中的所有节点能够在去信任的环境自由安全的交换数据,使得对“人”的信任改成了对机器的信任,任何人为的干预不起作用。
- 安全性(信息不可篡改) :数据在多个节点存储了多份,篡改数据得改掉51%节点的数据,这太难。同时,还有其它安全机制,如:比特币的每笔交易,都由付款人用私钥签名,证明确实是他同意向某人付款,其它人无法伪造。
- 匿名性(去信任) :由于节点之间的交换遵循固定的算法,其数据交互是无需信任的(区块链中的程序规则会自行判断活动是否有效),因此交易对手无须通过公开身份的方式让对方自己产生信任,对信用的累积非常有帮助。
(3)共识算法(博弈论) /全民记账
一般有: POW (工作量证明)、PoS (权益证明)、DPoS (股份授权证明机制)
比特币采用了POW (工作量证明) :
争夺记账权=挖矿
计算出来的账单节点哈希值前13个字符为0,则符合规则,得到记账权。
有一个节点计算出结果,则广播消息告知其它节点,其它节点更新数据。
相关文章:

软考系统架构师知识点集锦四:信息安全技术基础知识
一、考情分析 二、考点精讲 2.1信息加解密技术 2.1.1对称加密 概念:对称加密(又称为私人密钥加密/共享密钥加密) : 加密与解密使用同一密钥。特点:加密强度不高,但效率高;密钥分发困难。 (大量明文为了保证加密效率一般使用对称加密) 常见对称密钥加密算法:DES:…...

Vscode中不显示.ipynb文件单元格行号
找到设置,搜索line number: 看到下面那个Notebook: Line Numbers 控制单元格编辑器中行号的显示。,选择on即可;...
【Oracle】[INS-30131]执行安装程序验证所需的初始设置失败。
这里写目录标题 一、问题描述1 报错内容1.1 无法从节点“kotin”检索 exectask 的版本1.2 工作目录"xxx"无法在节点"kotin"上使用 2 相关环境2.1 安装软件2.2 安装系统 3 解决思路分析 二、解决方案1 方案一、 满足验证条件 - 不换系统1.1 第一步、检查文件…...

二进制部署kubernetes集群的推荐方式
软件版本: 软件版本containerdv1.6.5etcdv3.5.0kubernetesv1.24.0 一、系统环境 1.1 环境准备 角色IP服务k8s-master01192.168.10.10etcd、containerd、kube-apiserver、kube-scheduler、kube-controller-manager、kubele、kube-proxyk8s-node01后续etcd、conta…...

智能矩阵,引领商业新纪元!拓世方案:打破线上线下界限,开启无限营销可能!
在科技赋能商业大潮中,一切行业都在经历巨大变革,传统的营销策略被彻底改变,催生着无数企业去打造横跨线上线下、多维度、全方位的矩阵营销帝国。无数的成功案例已经告诉我们,营销不再只是宣传,而是建立品牌与消费者之…...
)
ADB原理(第四篇:聊聊adb shell ps与adb shell ps有无双引号的区别)
前言 对于经常使用adb的同学,不可避免的一定会这样用adb,比如我们想在手机里执行ps命令,于是在命令行中写下如下代码: adb shell ps -ef 或者 adb shell "ps -ef" 两种方式都可以使用,你喜欢用哪个呢&#…...
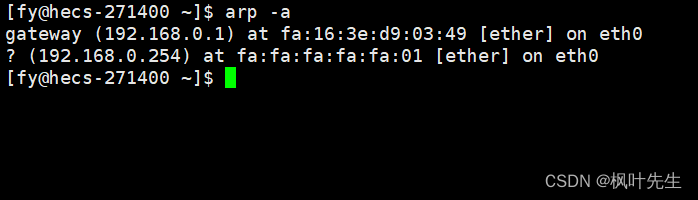
「网络编程」数据链路层协议_ 以太网协议学习
「前言」文章内容是数据链路层以太网协议的讲解。 「归属专栏」网络编程 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、以太网协议简介二、以太网帧格式(报头)三、MTU对上层协议的影响四、ARP协议4.1 ARP协议的作用4.2 ARP协议报头 一、以太网协…...
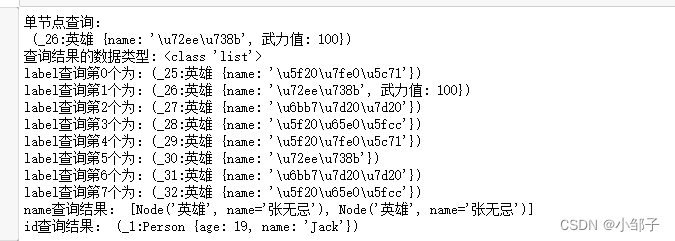
通过python操作neo4j
在neo4j中创建结点和关系 创建结点 创建电影结点 例如:创建一个Movie结点,这个结点上带有三个属性{title:‘The Matrix’, released:1999, tagline:‘Welcome to the Real World’} CREATE (TheMatrix:Movie {title:The Matrix, released:1999, tagl…...
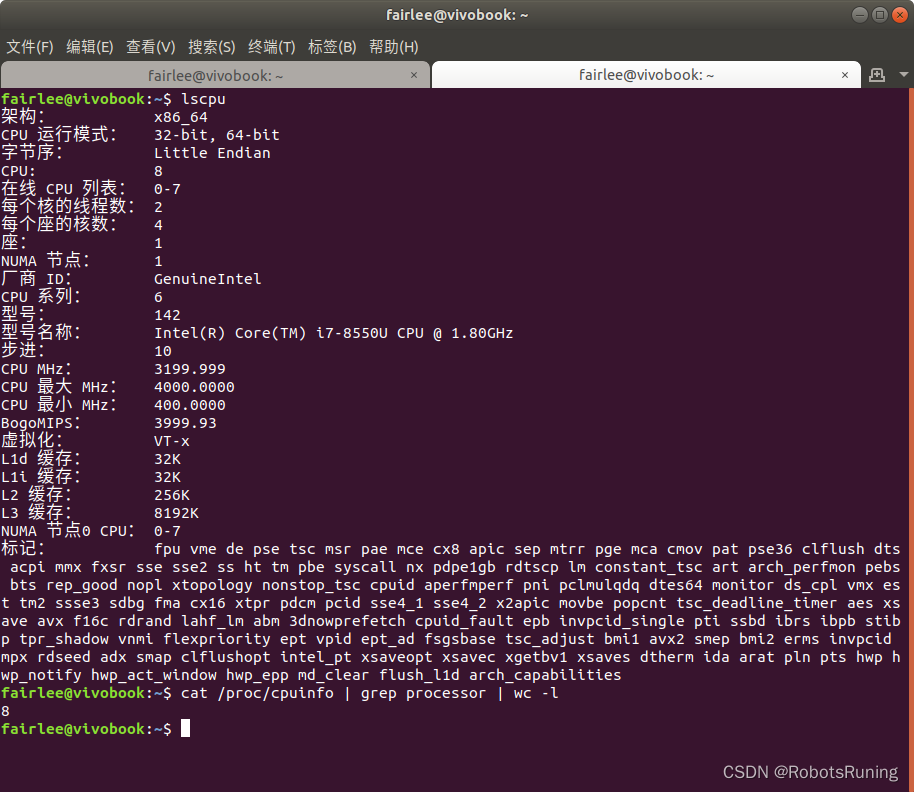
Ubuntu中查看电脑有多少个核——lscpu
1. 使用lscpu命令: 打开终端并输入以下命令: lscpu你会看到与CPU相关的详细信息。查找"CPU(s)"这一行来看总的核心数。另外,“Core(s) per socket”表示每个插槽或每个物理CPU的核数,“Socket(s)”表示物理CPU的数量。将这两个值相乘即得到总…...
)
Python学习笔记第七十二天(Matplotlib imread)
Python学习笔记第七十二天 Matplotlib imread读取图像数据修改图像裁剪图像图像颜色 后记 Matplotlib imread imread() 方法是 Matplotlib 库中的一个函数,用于从图像文件中读取图像数据。 imread() 方法返回一个 numpy.ndarray 对象,其形状是 (nrows,…...
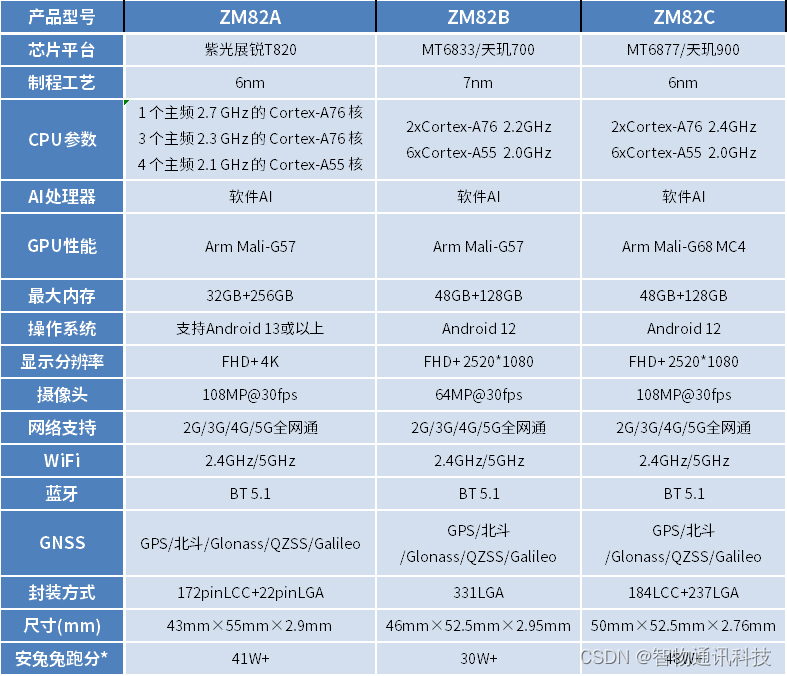
安卓核心板_天玑700、天玑720、天玑900_5G模块规格参数
5G安卓核心板是采用新一代蜂窝移动通信技术的重要设备。它支持万物互联、生活云端化和智能交互的特性。5G技术使得各类智能硬件始终处于联网状态,而物联网则成为5G发展的主要动力。物联网通过传感器、无线网络和射频识别等技术,实现了物体之间的互联。而…...

CS224W2.2——传统基于特征的方法(边层级特征)
在这篇中,我们介绍了链接预测的重要任务,以及如何提取链接级特征来更好地解决这类问题。这在我们需要预测缺失的边或预测将来会出现的边的情况下很有用。我们将讨论的链路级功能包括基于距离的功能,以及本地和全局邻域重叠。 文章目录 1. 边层…...
python—openpyxl操作excel详解
前言 openpyxl属于第三方模块,在python中用来处理excel文件。 可以对excel进行的操作有:读写、修改、调整样式及插入图片等。 但只能用来处理【 .xlsx】 后缀的excel文件。 使用前需要先安装,安装方法: pip install openpyxl…...
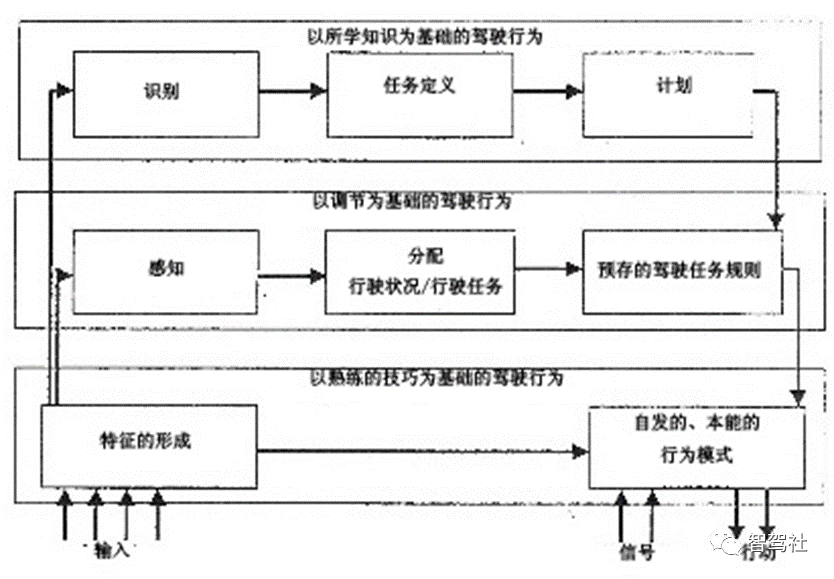
汽车行驶性能的主观评价方法(2)-驾驶员的任务
人(驾驶员)-车辆-环境闭环控制系统 驾驶过程中,驾驶员承担着操纵车辆和控制车辆的任务。驾驶员在不知不觉中接受了大量光学、声学和动力学信息并予以评价,同时不断地通过理论值和实际值的比较来完成控制作用(图 2.1&a…...
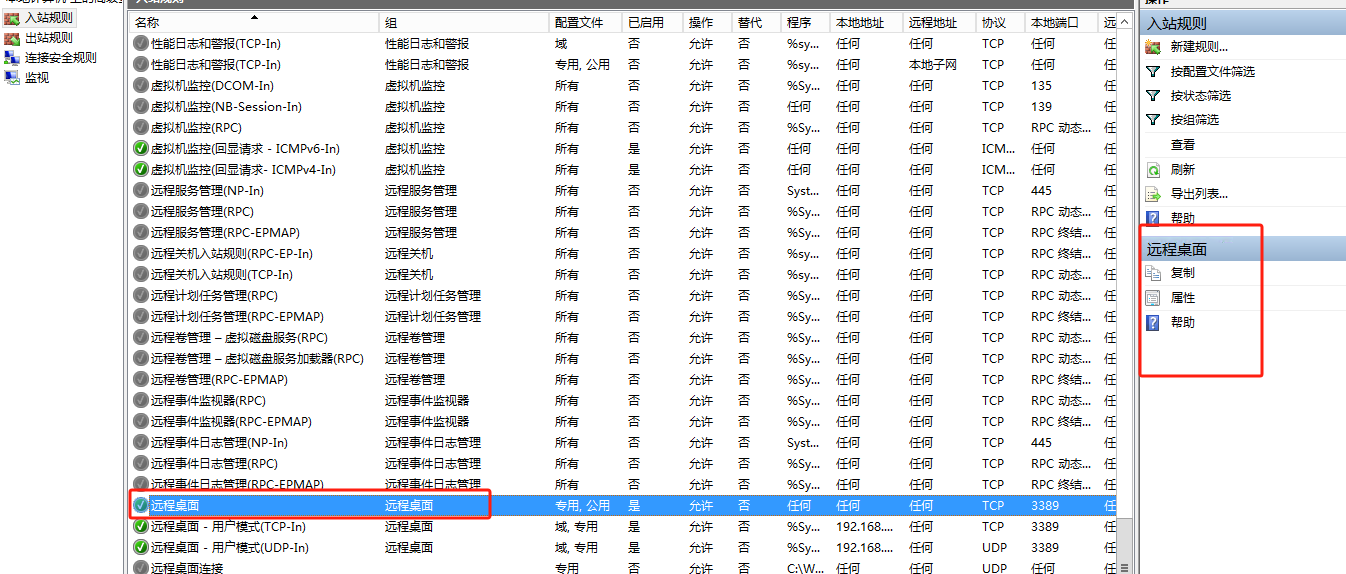
server2012 通过防火墙开启局域网内限定IP进行远程桌面连接
我这里需要被远程桌面的电脑系统版本为windows server2012 1、打开允许远程连接设置 2、开启防火墙 3、设置允许“远程桌面应用”通过防火墙 勾选”远程桌面“ 3、入站规则设置 高级设置→入站规则→远程桌面-用户模式(TCP-In) 进入远程桌面属性的作用域——>远程IP地址—…...
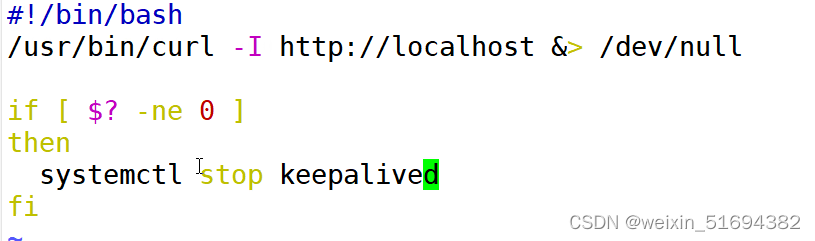
lvs+keepalived: 高可用集群
lvskeepalived: 高可用集群 keepalived为lvs应运而生的高可用服务。lvs的调度器无法做高可用,于是keepalived软件。实现的是调度器的高可用。 但是:keepalived不是专门为集群服务的,也可以做其他服务器的高可用。 lvs的高可用集群…...
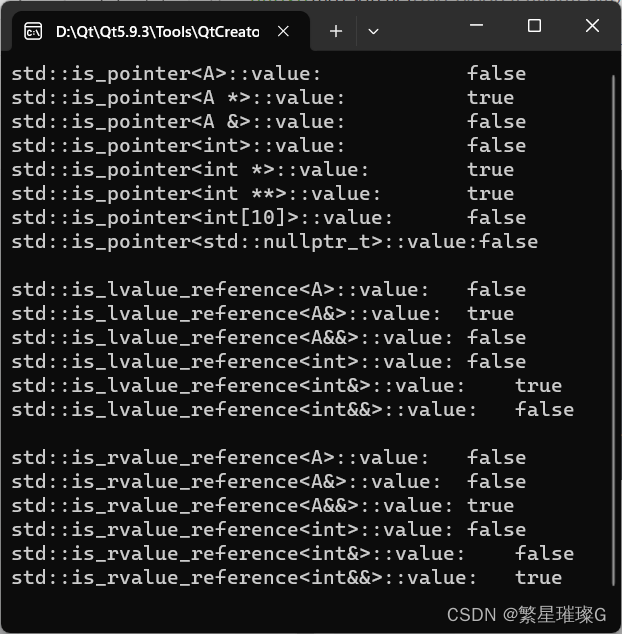
C++标准模板(STL)- 类型支持 (类型特性,is_pointer,is_lvalue_reference,is_rvalue_reference)
类型特性 类型特性定义一个编译时基于模板的结构,以查询或修改类型的属性。 试图特化定义于 <type_traits> 头文件的模板导致未定义行为,除了 std::common_type 可依照其所描述特化。 定义于<type_traits>头文件的模板可以用不完整类型实…...

C++——类和对象(上)
1.面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解决问题。 例如手洗衣服 C是基于面向对象的,关注的是对象,将一件事情拆分成不同的对象,靠对象之间…...
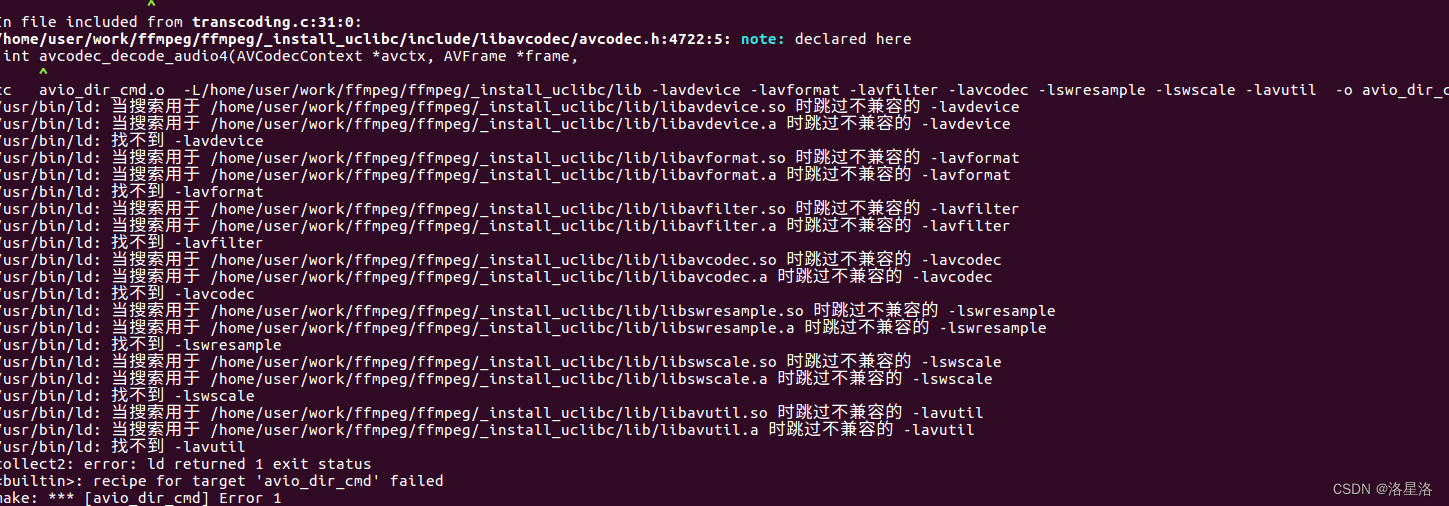
ffmpeg中examples编译报不兼容错误解决办法
ffmpeg中examples编译报不兼容错误解决办法 参考examples下的README可知,编译之前需要设置 PKG_CONFIG_PATH路径。 export PKG_CONFIG_PATH/home/user/work/ffmpeg/ffmpeg/_install_uclibc/lib/pkgconfig之后执行make出现如下错误: 基本都是由于库的版…...
图形旋转、镜像、缩放)
Python与CAD系列基础篇(十一)图形旋转、镜像、缩放
目录 0 简述1 图形旋转2 图形镜像3 图形缩放0 简述 本篇详细介绍使用①通过pyautocad连接AutoCAD进行处理②通过ezdxf处理dxf格式文件进行图形旋转、镜像、缩放的方法。 1 图形旋转 pyautocad方式 from pyautocad import Autocad, APoint, aDouble import mathacad = Autoca…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
