C# | Chaikin算法 —— 计算折线对应的平滑曲线坐标点

Chaikin算法——计算折线对应的平滑曲线坐标点
本文将介绍一种计算折线对应的平滑曲线坐标点的算法。该算法使用Chaikin曲线平滑处理的方法,通过控制张力因子和迭代次数来调整曲线的平滑程度和精度。通过对原始点集合进行切割和插值操作,得到平滑的曲线坐标点集合。实验结果表明,该算法能够有效地平滑折线,并且具有较高的精度和可控性。
文章目录
- Chaikin算法——计算折线对应的平滑曲线坐标点
- 引言
- 算法
- 算法流程
- Chaikin曲线平滑处理
- 实验与结果
- 测试1:验证不同迭代次数下的算法结果
- 测试2:观察不同张力因子下的算法结果
- 结论
- 参考资料
引言
在计算机图形学和数据可视化领域,平滑曲线的生成是一个重要的问题。平滑曲线可以使得数据更加易于理解和分析,同时也可以提高图形的美观性。折线是一种常见的曲线表示方法,但是折线本身具有较高的噪声和锯齿状的特点,需要进行平滑处理。本文提出了一种基于Chaikin曲线平滑处理的算法,可以将折线转化为平滑的曲线。
算法
算法流程
流程的具体步骤如下:
- 检查输入的坐标点集合的合法性,确保至少有3个坐标点。
- 对输入的参数进行范围约束,确保迭代次数大于等于1,张力因子在0到1之间。
- 将张力因子映射到0.05到0.45之间,以便在计算切割距离时使用。
- 迭代计算,使用Chaikin曲线平滑处理的方法对坐标点集合进行处理。
- 返回平滑后的曲线坐标点集合。
/// <summary>/// 计算折线对应的平滑曲线坐标点/// </summary>/// <param name="points">坐标集合</param>/// <param name="tension">张力因子[0,1],用于控制曲线的平滑程度。张力因子越小时切割点会越靠近线段的起始点,反之会靠近线段的结束点。</param>/// <param name="iterationCount">迭代次数,用于控制曲线平滑的精度</param>/// <returns></returns>/// <exception cref="ArgumentException"></exception>private List<Point> SmoothCurveChaikin(Point[] points, float tension = 0.5f, byte iterationCount = 1){// 坐标点合法性检查if (points == null || points.Length < 3){throw new ArgumentException("至少需要3个坐标点。", nameof(points));}// 参数范围约束iterationCount = Math.Max(iterationCount, (byte)1);tension = Math.Max(tension, 0);tension = Math.Min(tension, 1);// 参数的限制在0到1之间是为了简化参数的使用和理解。将张力因子的取值范围映射到0到1之间,使得参数的范围更加直观和易于控制。// 通过将张力因子乘以0.4并加上0.05,可以将0到1之间的参数映射到0.05到0.45之间,以便在计算切割距离时使用。// 张力因子在这里用于控制曲线的平滑程度。具体来说,张力因子定义了线段半长切角距离的一个尺度,取值范围在0.05到0.45之间。// 当张力因子为0.5时,相当于使用了经典的Chaikin算法,即将每个线段切割成四分之一和四分之三的两个点。这样可以保持曲线的对称性。double cutdist = 0.05 + (tension * 0.4);// 迭代计算List<Point> lst = points.ToList();for (int i = 1; i <= iterationCount; i++){lst = SmoothChaikin(lst, cutdist);}return lst;}
Chaikin曲线平滑处理
Chaikin曲线平滑处理是一种基于切割和插值的方法,通过对线段进行切割和插值操作,得到平滑的曲线。
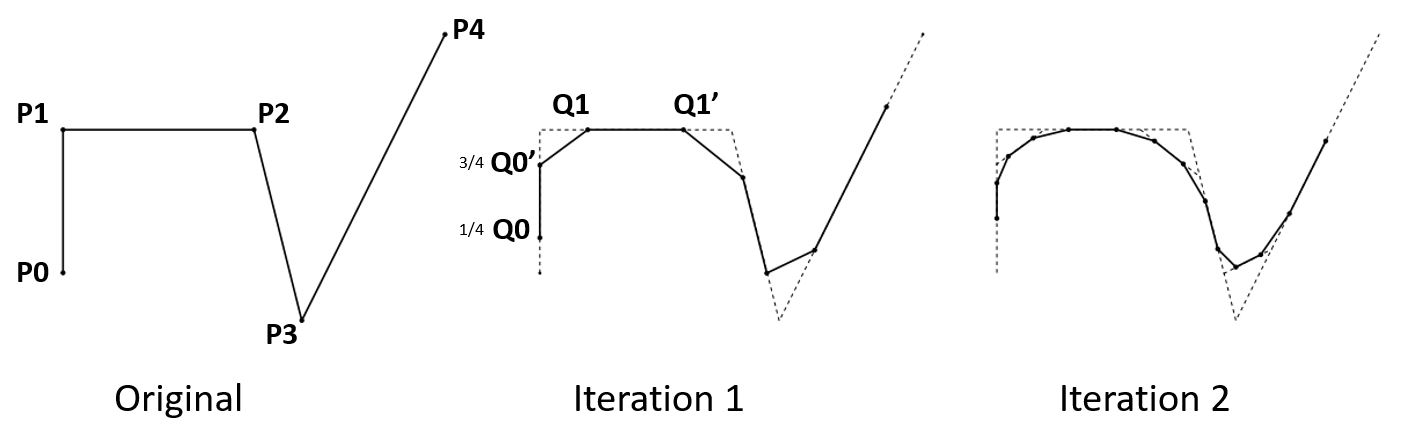
具体步骤如下:
- 添加第一个点,即原始点集合的第一个点。
- 将每一个点拆分成前后两个点,通过计算切割距离参数和原始点的坐标进行插值计算。
- 添加插值计算得到的两个点。
- 添加最后一个点,即原始点集合的最后一个点。
- 返回平滑后的曲线坐标点集合。
/// <summary>/// 对点集合进行Chaikin曲线平滑处理/// </summary>/// <param name="points">要进行平滑处理的曲线的原始点</param>/// <param name="cuttingDist">切割距离参数,用于定义线段切割的尺度。取值范围通常在0.05到0.45之间,用于控制曲线的平滑程度</param>/// <returns></returns>private List<Point> SmoothChaikin(List<Point> points, double cuttingDist){// 添加第一个点List<Point> nl = new List<Point> { points[0] };// 将每一个点拆分成前后两个点Point q, r;for (int i = 0; i < points.Count - 1; i++){q = new Point((int)Math.Round(((1 - cuttingDist) * points[i].X + cuttingDist * points[i + 1].X)),(int)Math.Round(((1 - cuttingDist) * points[i].Y + cuttingDist * points[i + 1].Y)));r = new Point((int)Math.Round((cuttingDist * points[i].X + (1 - cuttingDist) * points[i + 1].X)),(int)Math.Round((cuttingDist * points[i].Y + (1 - cuttingDist) * points[i + 1].Y)));nl.Add(q);nl.Add(r);}// 添加最后一个点nl.Add(points.Last());return nl;}
实验与结果
为了验证算法的有效性和可靠性,我们进行了两组测试。
测试1:验证不同迭代次数下的算法结果
测试步骤:
- 将张力因子设置为0.5。
- 调整迭代次数为1、2、3。
- 对比不同迭代次数下的算法结果。
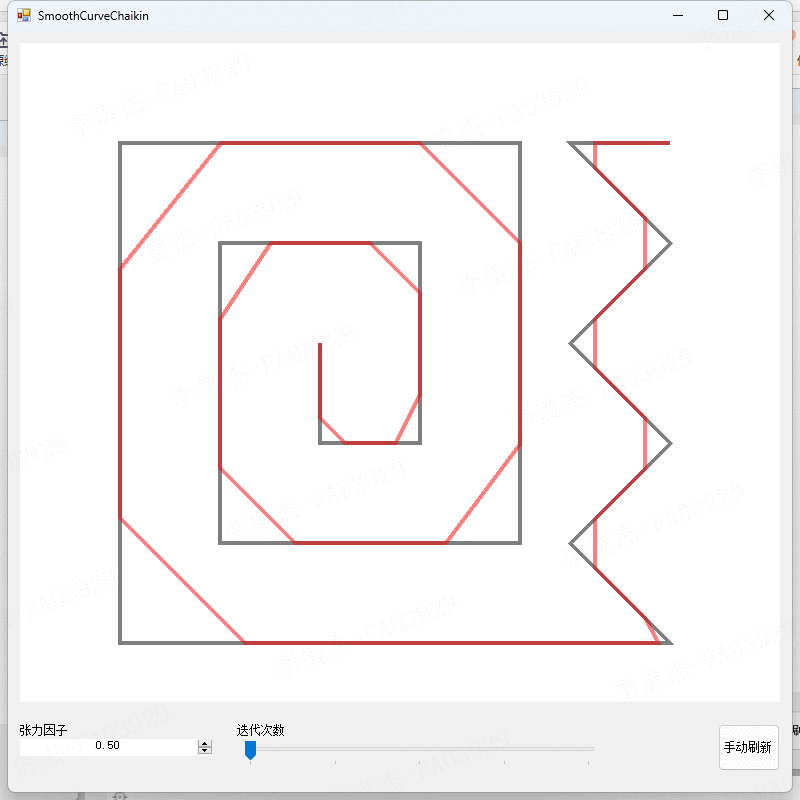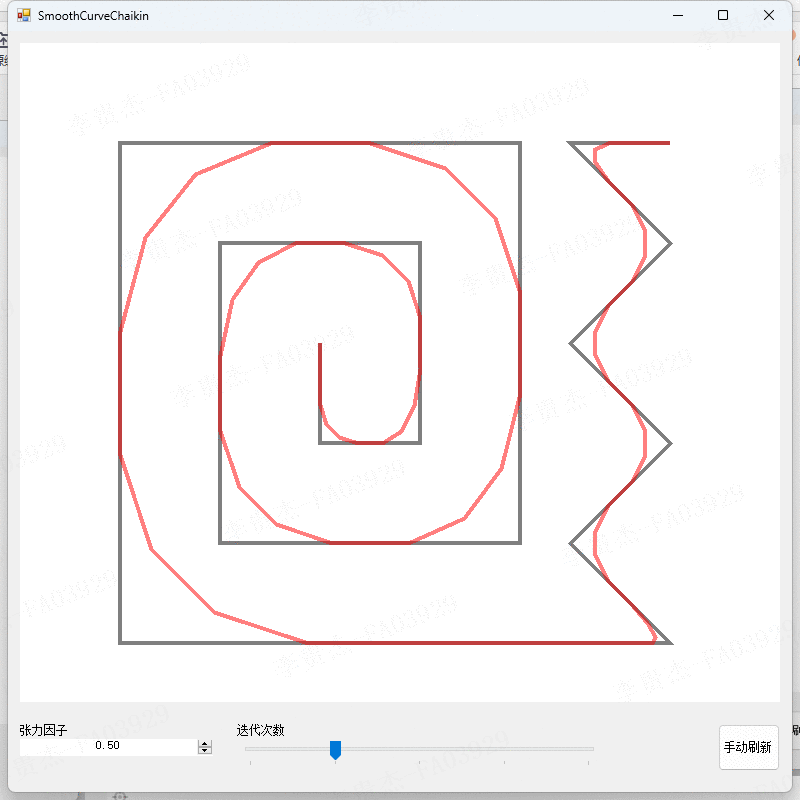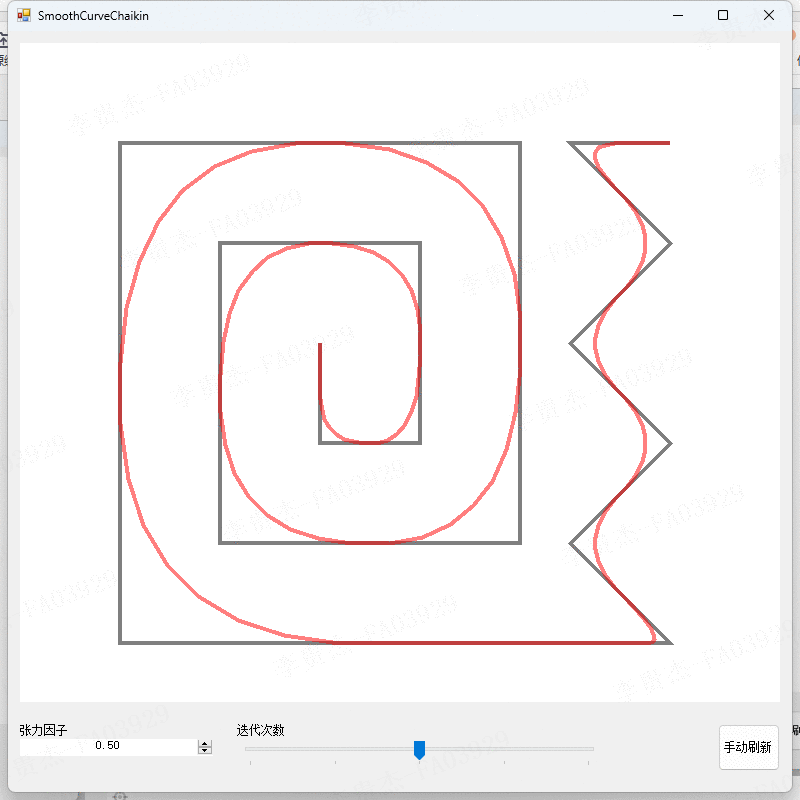
测试2:观察不同张力因子下的算法结果
测试步骤:
- 将迭代次数设置为1。
- 调整张力因子为0、0.2、0.4、0.6、0.8。
- 观察不同张力因子下的算法结果。
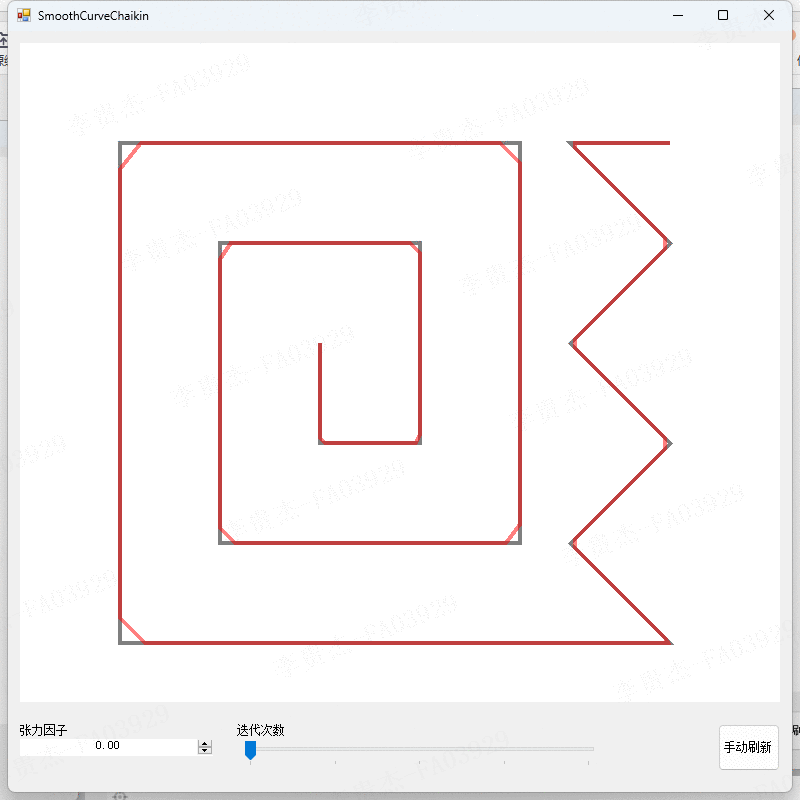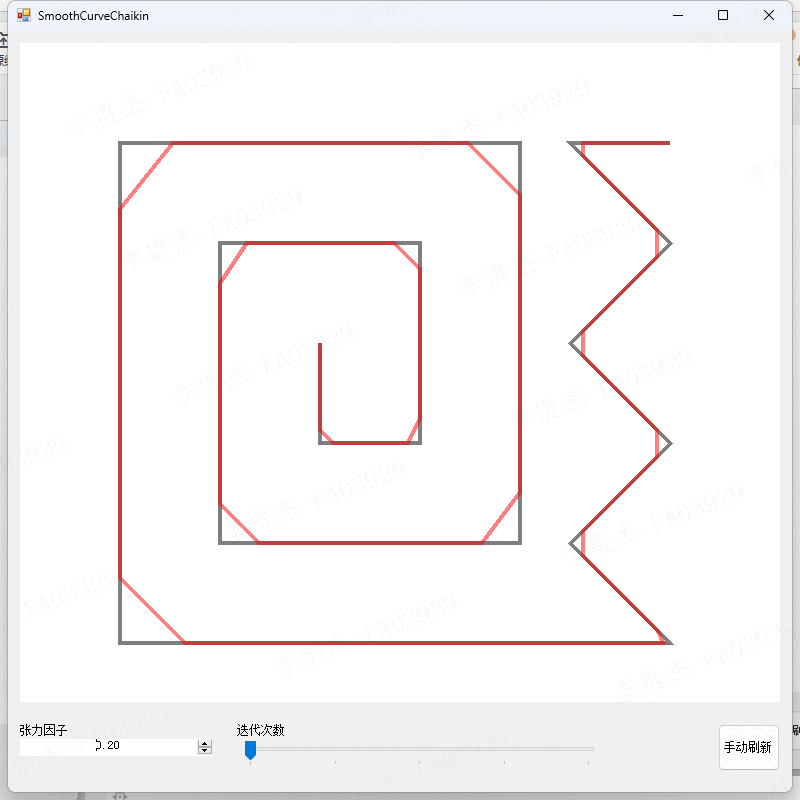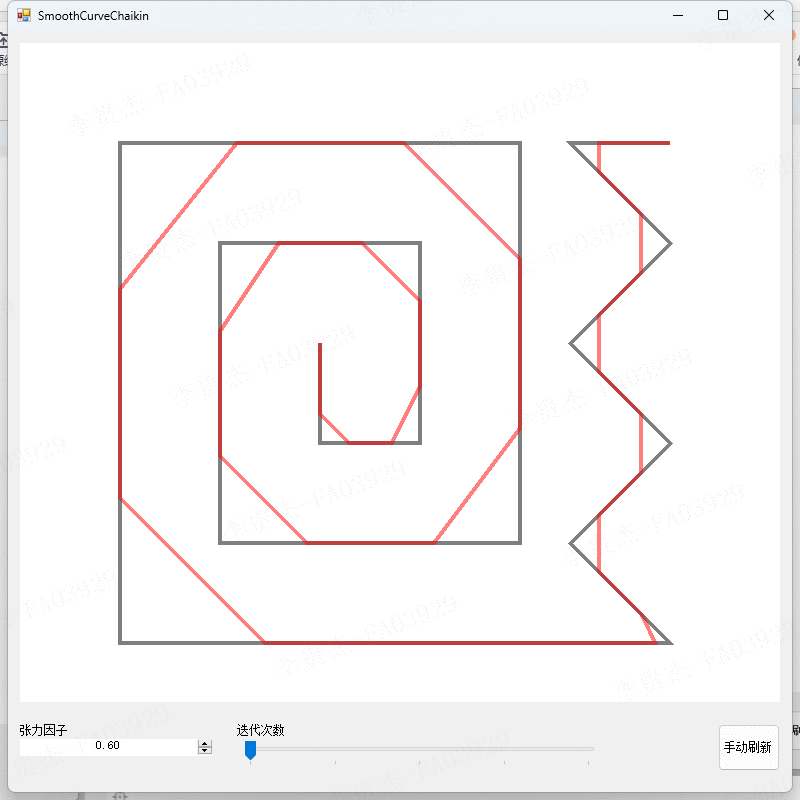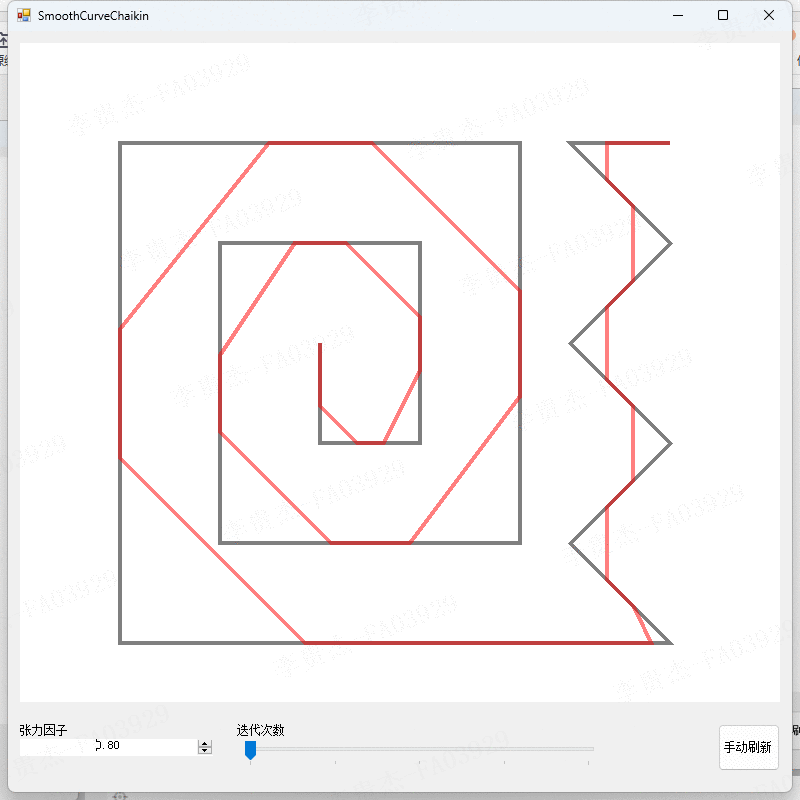
本算法在不同的参数设置下进行了实验,得到了不同平滑程度和精度的曲线。实验结果表明,当张力因子较小时,切割点会靠近线段的起始点,曲线的平滑程度较低;当张力因子较大时,切割点会靠近线段的结束点,曲线的平滑程度较高。迭代次数的增加可以提高曲线的平滑精度,但也会增加计算的时间复杂度。实验结果还表明,本算法能够有效地平滑折线,并且具有较高的精度和可控性。
结论
本文介绍了一种计算折线对应的平滑曲线坐标点的算法。该算法使用Chaikin曲线平滑处理的方法,通过控制张力因子和迭代次数来调整曲线的平滑程度和精度。实验结果表明,该算法能够有效地平滑折线,并且具有较高的精度和可控性。未来的工作可以进一步优化算法的性能和扩展算法的应用范围。
参考资料
- 2D Polyline Vertex Smoothing
相关文章:

C# | Chaikin算法 —— 计算折线对应的平滑曲线坐标点
Chaikin算法——计算折线对应的平滑曲线坐标点 本文将介绍一种计算折线对应的平滑曲线坐标点的算法。该算法使用Chaikin曲线平滑处理的方法,通过控制张力因子和迭代次数来调整曲线的平滑程度和精度。通过对原始点集合进行切割和插值操作,得到平滑的曲线坐…...

day44
什么是前端 前端是所有跟用户直接打交道的都可以称之为是前端 比如:pc页面、手机页面、平板页面、汽车显示屏等等显示出来的都是前端内容 什么是后端? 就是一堆代码,用户不能够直接看到,不直接与用户打交道的都是后端 常见的后端…...

python常用操作汇总
python创建二维数组 python创建三行三列的二维数组,下面方法是错误的,因为是浅拷贝: lst1 [0] * 3 lst2 [lst1] * 3 lst2[1][1] 2 print(lst2) # [[0, 2, 0], [0, 2, 0], [0, 2, 0]]正确姿势 lst [[0 for j in range(3)] for i in ran…...

赴日IT培训 日本IT行业为啥吃香?
确实现在有许多小伙伴尝到了赴日IT的甜头,可是去日本从事IT行业真的很简单吗?为什么日本的IT行业这么缺人呢?那今天小编就跟大家聊一聊日本的IT行业。 咱们先来说说日本的IT行业为什么缺人?其实不只是IT行业,可以说日…...

2016年亚太杯APMCM数学建模大赛A题基于光学信息数据的温度及关键元素含量预测求解全过程文档及程序
2016年亚太杯APMCM数学建模大赛 A题 基于光学信息数据的温度及关键元素含量预测 原题再现 光含有能量,在一定条件下可以转化为热。燃烧是一种常见的现象,既能发光又能发热。光和热通常是同时存在的,一般来说,光强度越高…...

一文讲明:企业知识库的作用和搭建方法
在现代商务环境中,企业面临着大量的信息和知识流动。这些信息和知识散落在各个部门、团队甚至个人之间,难以进行有效的整合和利用。而企业知识库的出现解决了这一问题。它提供了一个统一的平台,将分散的信息汇聚到一个集中的数据库中…...

技术的新浪潮:从SOCKS5代理到跨界电商的未来
在当今这个日新月异的技术时代,各种创新技术如雨后春笋般涌现。从SOCKS5代理到跨界电商,再到爬虫技术、出海战略和游戏产业的飞速发展,我们正处于一个技术变革的黄金时代。 SOCKS5代理:安全的网络通道 SOCKS5代理是一种网络协议…...
Android intent的一些小使用
目录: 1. Test5.java2. activity_main5.xml3. Empty.java (这个是用来带参数打开Activity按钮用的)4. activity_empty.xml5. 总结 一些基本的问题就不进行说明了,直接上代码!!! // 最后的隐形intent和带返回值没有解决…...

Android 关闭 SELinux 释放权限限制
Android 关闭 SELinux 释放权限限制 接前一篇,后续收到客户需求想要关闭 SELinux 放开安全权限,SELinux 是 Linux 的一个安全子系统,SELinux 主要作用是最大限度地减小系统中服务进程可访问的资源,我们想要放开安全权限只需处理 …...

国际腾讯云自主拼装直播 URL教程!!!
注意事项 创建转码模板 并与播放域名进行 绑定 后,转码配置后的直播流,需将播放地址的 StreamName 拼接为 StreamName_转码模板名称,更多详情请参见 播放配置。 前提条件 已注册腾讯云账号,并开通 腾讯云直播服务。 已在 域名…...
AQS 为什么要使用双向链表?
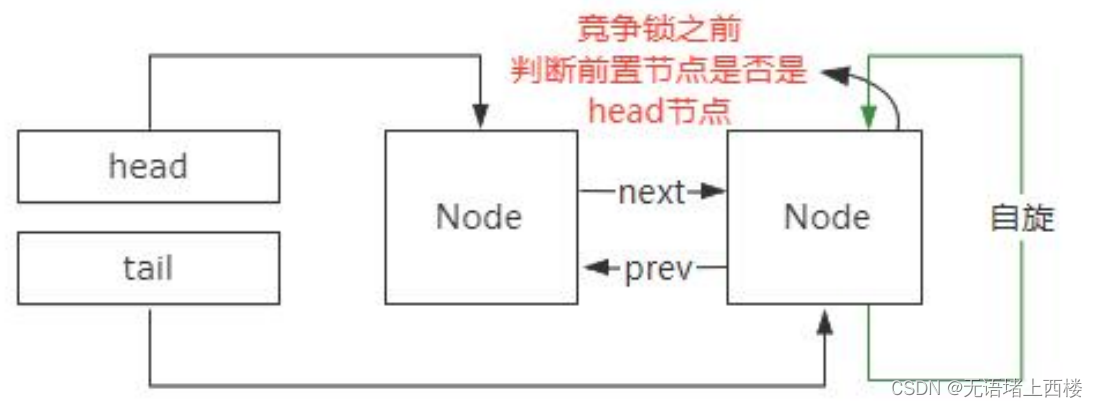
双向链表 双向链表的特点是它有两个指针,一个指针指向前置节点,一个指针指向后继节点。所以,双向链表可以支持 常量 O(1) 时间复杂度的情况下找到前驱结点,基于这样的特点。双向链表在插入和删除操作的时候,要比单向链…...

Golang 自定义函数库(个人笔记)
1.用字符串连接切片元素(类似php implode) package mainimport ("fmt""strconv""strings" )func main() {data : []int{104, 101, 108, 108, 111}fmt.Println(IntSliceToString(data, ",")) }func IntSliceToS…...

openlayers 地图组件封装
openlayers 地图组件封装 <template><div class"mapBox"><!-- 地图 --><div ref"map" id"map" class"map"></div><!-- 点位弹窗 --><div id"popup" class"ol-popup">…...

【算法设计与分析】—— 分治算法
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...
Unable to find GatewayFilterFactory with name TokenRelay
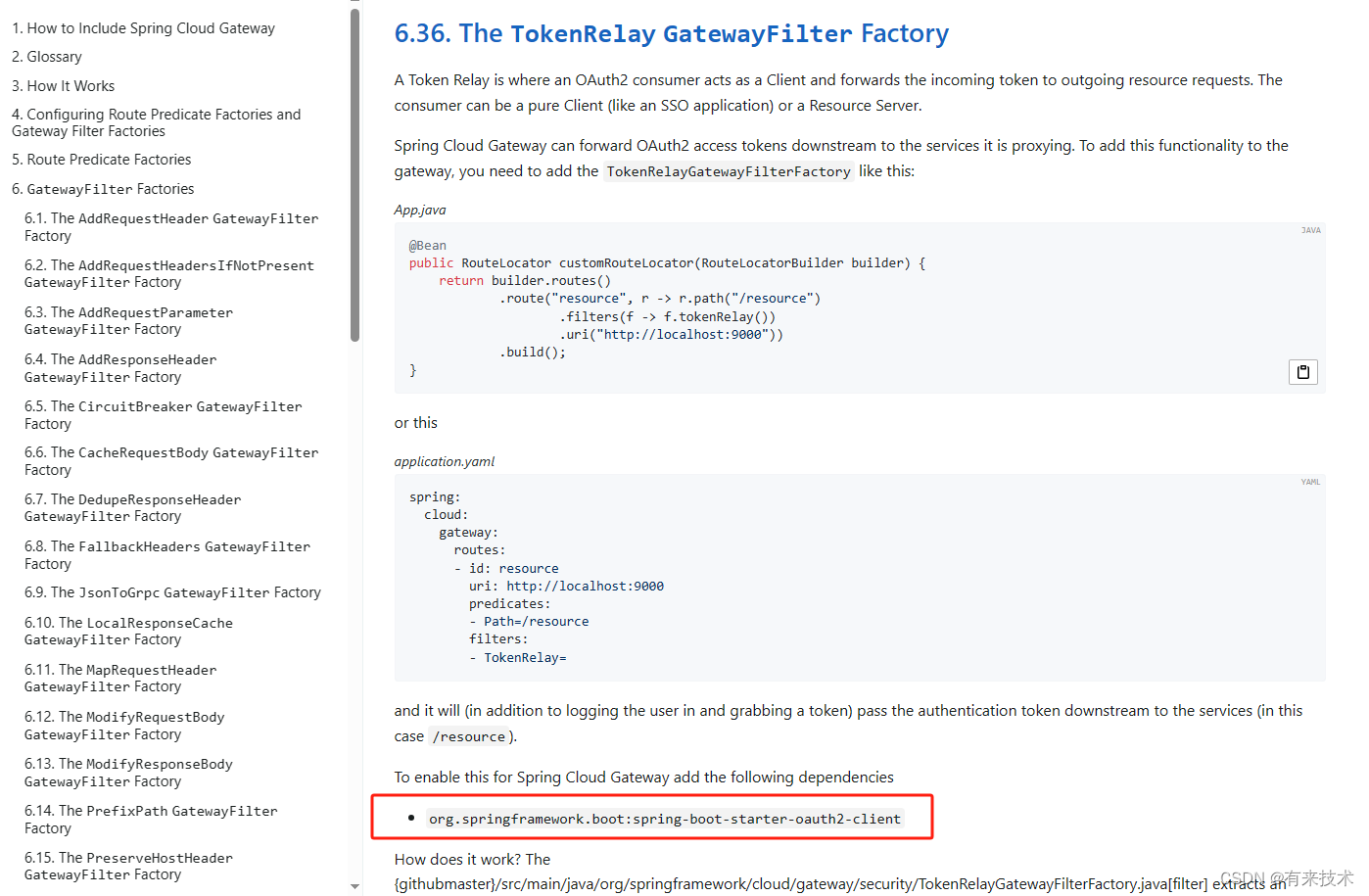
目录 问题分析解决方案参考文档开源项目微服务商城项目前后端分离项目 问题分析 Spring Cloud Gateway 网关作为代理资源服务器,需要将 JWT 传递给下游资源服务器,下面是网关的配置 spring:cloud:gateway:discovery:locator:enabled: true # 启用服务发…...
竞赛 深度学习大数据物流平台 python
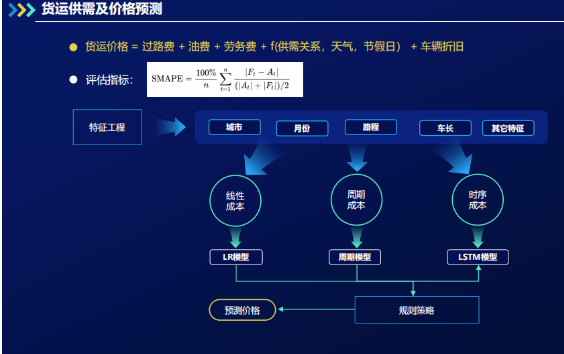
文章目录 0 前言1 课题背景2 物流大数据平台的架构与设计3 智能车货匹配推荐算法的实现**1\. 问题陈述****2\. 算法模型**3\. 模型构建总览 **4 司机标签体系的搭建及算法****1\. 冷启动**2\. LSTM多标签模型算法 5 货运价格预测6 总结7 部分核心代码8 最后 0 前言 ǵ…...

git基础及原理相关解析
git入门 结构基本操作help提交分支git merge和git rebase对比 拉取 git文档 结构 工作区:电脑目录中能看到的文件暂存区:使用git add *操作提交文件的位置,一般位于.git\index,这个文件里面存储了当前位于暂存区的所有文件的校验…...

【Python机器学习】零基础掌握isotonic_regression等渗回归
遇到了数据不一致的困扰吗? 在市场分析、医疗研究或者其他数据密集型领域,经常会遇到一个问题:如何从一组不完全一致或者有噪音的数据中提取出有用的信息?例如,假设一家餐厅想要根据顾客的评分和消费金额来调整菜单。 顾客评分消费金额(元)顾客年龄访问次数4.21002533.…...

支持宏的文本编辑器提高生产力
场景 我们知道很多文本/代码编辑器支持宏的录制、重放、保存,甚至可以与快捷键命令结合的功能,快速实现重放宏的操作。 如果您的编辑器支持宏这项功能,请多使用 😃 宏化自动步骤相当于对编辑器的自动化编程,宏录制可…...
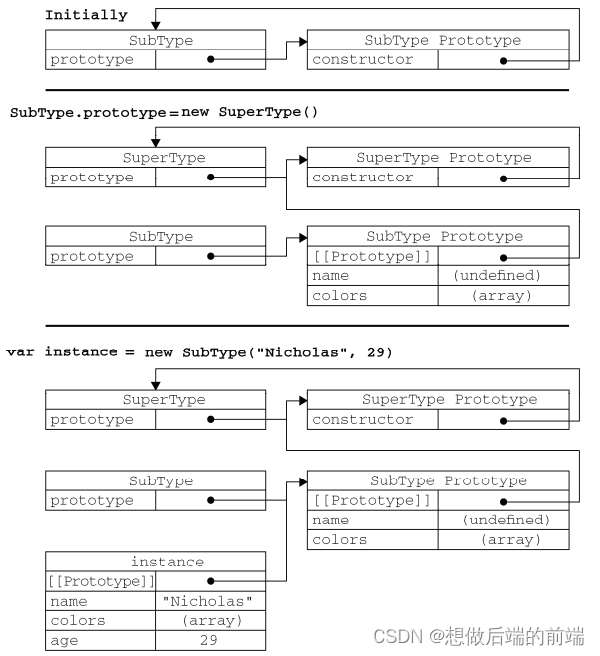
JS中面向对象的程序设计
面向对象(Object-Oriented,OO)的语言有一个标志,那就是它们都有类的概念,而通过类可以创建任意多个具有相同属性和方法的对象。但在ECMAScript 中没有类的概念,因此它的对象也与基于类的语言中的对象有所不…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
