【算法设计与分析】—— 分治算法
🎃个人专栏:
🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客
🐳Java基础:Java基础_IT闫的博客-CSDN博客
🐋c语言:c语言_IT闫的博客-CSDN博客
🐟MySQL:数据结构_IT闫的博客-CSDN博客
🐠数据结构:数据结构_IT闫的博客-CSDN博客
💎C++:C++_IT闫的博客-CSDN博客
🥽C51单片机:C51单片机(STC89C516)_IT闫的博客-CSDN博客
💻基于HTML5的网页设计及应用:基于HTML5的网页设计及应用_IT闫的博客-CSDN博客
🥏python:python_IT闫的博客-CSDN博客
欢迎收看,希望对大家有用!
目录
🎯目的:
🎯问题及代码分析:
🥽1)二分查找的实现:
🎃代码及解析:
💻导入必要的类:
💻 创建 One 类:
💻 在 main 方法中执行二分查找:
💻 binarySearchHelper 方法实现二分查找:
🥽2)最小值问题:求n个元素的最小值:
🎃代码及解析:
💻导入必要的类:
💻 创建 One 类:
💻 在 main 方法中执行查找最小值操作:
💻 findMinmumHelper 方法实现递归查找最小值:
🥽3)幂乘问题: 给定实数a和自然数n,求a^n:
🎃代码及解析:
💻导入了Scanner类:
💻main函数:
💻power方法:
🥽快速排序的实现:
🎃代码及解析:
💻导入了java.util.Arrays类:
💻main方法:
💻 快速排序算法:
💻 分割数组:
💻 交换数组中两个元素的位置:
🎯总结分治算法的特点:
🎯注:所有完整代码:
🎯目的:
1)了解分治策略算法思想及基本原理;
2)掌握使用分治算法求解问题的一般特征;
3)掌握分解、治理的方法;
4)能够针对实际问题,能够正确的分解、治理,设计分治算法;
5)能够正确分析算法的时间复杂度和空间复杂度。
🎯问题及代码分析:
🥽1)二分查找的实现:
🎃代码及解析:
💻导入必要的类:
分析:这行代码导入了 java.util.Scanner 类,用于从控制台读取用户的输入。
import java.util.Scanner;💻 创建 One 类:
分析:这段代码定义了一个名为 One 的公共类,并包含了 main 方法和 binarySearchHelper 方法。
public class One {public static void main(String[] args) {// ...}public static int binarySearchHelper(int[] arr, int target, int low, int high) {// ...}
}💻 在 main 方法中执行二分查找:
分析:
这段代码首先创建了一个 Scanner 对象 scan,用于读取用户的输入。然后,定义了一个有序整数数组 arr,其中包含了数字 1、3、4、7、8 和 10。
接下来,通过 System.out.println 打印提示信息,要求用户输入一个在 10 以内的数字。然后,使用 scan.nextInt() 从控制台读取用户输入的目标数字,并将其存储在变量 target 中。
最后,调用 binarySearchHelper 方法进行二分查找,传入数组 arr、目标数字 target、数组的起始索引 0 和结束索引 arr.length - 1。根据返回的索引值,打印相应的结果。
Scanner scan = new Scanner(System.in);
int[] arr = {1, 3, 4, 7, 8, 10};
System.out.println("请输入您要查找的10以内的数字:");
int target = scan.nextInt();
int index = binarySearchHelper(arr, target, 0, arr.length - 1);
if (index < 0) {System.out.println("您输入的数字查找不到!");
} else {System.out.println("输入数字对应为索引为:" + index);
}
💻 binarySearchHelper 方法实现二分查找:
分析:
这段代码定义了一个递归方法 binarySearchHelper,用于在给定的有序整数数组 arr 中查找目标数字 target。方法接受四个参数:数组 arr、目标数字 target、数组的起始索引 low 和结束索引 high。
在方法中,首先检查起始索引是否大于结束索引,如果是,则表示目标数字不在数组中,返回 -1。
否则,计算中间索引 mid,并检查中间元素是否等于目标数字。如果是,返回中间索引 mid。
如果中间元素大于目标数字,则递归调用 binarySearchHelper 方法,在左半部分数组中继续查找目标数字。
如果中间元素小于目标数字,则递归调用 binarySearchHelper 方法,在右半部分数组中继续查找目标数字。
这样,通过递归调用,最终会找到目标数字的索引值或返回 -1,表示目标数字不存在于数组中。
public static int binarySearchHelper(int[] arr, int target, int low, int high) {if (low > high) {return -1;}int mid = (low + high) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] > target) {return binarySearchHelper(arr, target, low, mid - 1);} else {return binarySearchHelper(arr, target, mid + 1, high);}
}
🥽2)最小值问题:求n个元素的最小值:
🎃代码及解析:
💻导入必要的类:
分析:这行代码导入了 java.util.Arrays 类,用于打印数组的内容。
import java.util.Arrays;
💻 创建 One 类:
分析:这段代码定义了一个名为 One 的公共类,并包含了 main 方法和 findMinmumHelper 方法。
public class One {public static void main(String[] args) {// ...}public static int findMinmumHelper(int[] arr, int low, int high) {// ...}
}
💻 在 main 方法中执行查找最小值操作:
分析:
这段代码首先定义了一个整型数组 arr,其中包含了一些整数。
接下来,调用 findMinmumHelper 方法进行查找最小值的操作,传入数组 arr、起始索引 0 和结束索引 arr.length - 1。将返回的最小值存储在变量 x 中。
最后,使用 System.out.println 打印数组的内容和最小值。
int[] arr = {90, 40, 50, 10, 99, 20};
int x = findMinmumHelper(arr, 0, arr.length - 1);
System.out.println("在数组" + Arrays.toString(arr));
System.out.println("最小值为:" + x);
💻 findMinmumHelper 方法实现递归查找最小值:
分析:
这段代码定义了一个递归方法 findMinmumHelper,用于在给定的数组 arr 中查找最小值。方法接受三个参数:数组 arr、起始索引 low 和结束索引 high。
在方法中,首先检查起始索引和结束索引是否相等,如果相等,则表示只有一个元素,直接返回该元素作为最小值。
否则,计算中间索引 mid,并分别递归调用 findMinmumHelper 方法,在左半部分数组和右半部分数组中查找最小值。
最后,使用 Math.min 方法比较左半部分数组的最小值 leftMin 和右半部分数组的最小值 rightMin,返回较小的值作为整个数组的最小值。
public static int findMinmumHelper(int[] arr, int low, int high) {if (low == high) {return arr[low];}int mid = (low + high) / 2;int leftMin = findMinmumHelper(arr, low, mid);int rightMin = findMinmumHelper(arr, mid + 1, high);return Math.min(leftMin, rightMin);
}
🥽3)幂乘问题: 给定实数a和自然数n,求a^n:
🎃代码及解析:
💻导入了Scanner类:
import java.util.Scanner;💻main函数:
分析:
在main方法中,通过Scanner类获取用户输入的a和n的值,并调用power方法计算a的n次方。
public static void main(String[] args) {// TODO Auto-generated method stubScanner scan=new Scanner(System.in);System.out.println("请输入a的值:");int a=scan.nextInt();System.out.println("请输入数字n的值");int n=scan.nextInt();int x=power(a,n);System.out.println(a+"的"+n+"次方为:"+x);}💻power方法:
分析:
-
power方法是一个递归方法,其参数为底数a和指数n。如果n等于0,则返回1,因为任何数的0次方都等于1。
-
如果n不等于0,则继续递归计算power(a,n/2)的值,即将指数除以2,以此来减少递归次数。
-
如果n是偶数,则直接返回temp*temp的值,即将计算结果平方。
-
如果n是奇数,则需要再乘上a,即返回atemptemp的值。
-
最终在main方法中输出计算结果。
public static int power(int a,int n){if(n==0) {return 1;}int temp=power(a,n/2);if(n%2==0) {return temp*temp;}else {return a*temp*temp;}}
}🥽快速排序的实现:
🎃代码及解析:
💻导入了java.util.Arrays类:
import java.util.Arrays;💻main方法:
分析:
-
定义了一个名为
One的Java类,并在其中实现了main()方法。 -
定义了一个整数数组
arr,并初始化为{9,10,44,33,4,15}。 -
使用
Arrays.toString()方法将数组转换为字符串,并输出排序前的序列。 -
调用
quickSort()方法对数组进行排序。 -
使用
Arrays.toString()方法将数组转换为字符串,并输出排序后的序列
public static void main(String[] args) {int [] arr= {9,10,44,33,4,15};System.out.println("排序前的序列为:"+Arrays.toString(arr));quickSort(arr,0,arr.length-1);System.out.println("排序后的序列为:"+Arrays.toString(arr));}💻 快速排序算法:
分析:
-
定义了一个名为
quickSort()的方法,用于实现快速排序算法。该方法的参数为要排序的数组、起始位置和结束位置。如果起始位置小于结束位置,说明还需要继续排序。 -
调用
partition()方法将数组分成两部分,返回枢轴元素的下标pivotIndex。 -
递归调用
quickSort()方法对左边的子数组进行排序,即从low到pivotIndex-1。 -
递归调用
quickSort()方法对右边的子数组进行排序,即从pivotIndex到high。
public static void quickSort(int [] arr,int low,int high) {if(low <high) {int pivotIndex=partition(arr,low,high);quickSort(arr, low,pivotIndex-1);quickSort(arr, pivotIndex, high);}}💻 分割数组:
分析:
-
定义了一个名为
partition()的方法,用于将数组分成两部分,左边的部分小于枢轴元素,右边的部分大于等于枢轴元素。该方法的参数为要排序的数组、起始位置和结束位置。 -
将枢轴元素设为数组的最后一个元素
arr[high]。 -
定义一个指针
i,指向数组的起始位置low-1。 -
使用for循环遍历数组中从
low到high-1的所有元素arr[j]。 -
如果
arr[j]小于枢轴元素pivot,则将i指针向右移动一位,并交换arr[i]和arr[j]的值,以确保左边的部分都小于枢轴元素。 -
将枢轴元素
pivot与arr[i+1]交换位置,并返回i+1作为新的枢轴元素下标。
public static int partition(int [] arr,int low,int high) {int pivot=arr[high];int i=low -1;for(int j=low;j<high;j++) {if(arr[j]<pivot) {i++;swap(arr,i,j);}}swap(arr,i+1,high);return i+1;}💻 交换数组中两个元素的位置:
分析:
定义了一个名为swap()的方法,用于交换数组中两个元素的位置。该方法的参数为要交换的数组和两个元素的下标。
public static void swap(int [] arr,int i,int j) {int temp=arr[i];arr[i]=arr[j];arr[j]=temp;}🎯总结分治算法的特点:
分治算法是一种常用的问题解决方法,其特点如下:
分解(Divide):将原问题划分为若干个子问题,每个子问题的规模较小且结构与原问题相似。
解决(Conquer):递归地解决每个子问题。如果子问题规模足够小,可以直接求解。
合并(Combine):将子问题的解合并成原问题的解。
分治算法的特点有以下几个方面:
适用性广泛:分治算法适用于解决各种类型的问题,包括排序、搜索、图算法等。只要问题可以被划分成若干个规模较小的子问题,并且这些子问题的解可以合并成原问题的解,就可以使用分治算法。
提高效率:通过将问题划分为多个子问题并并行处理,分治算法可以显著提高问题的解决效率。子问题之间相互独立,可以同时进行计算,从而充分利用计算资源。
递归思想:分治算法通常使用递归来解决子问题。递归调用使得问题的规模逐渐减小,直到达到基本情况,然后再逐步合并子问题的解来得到原问题的解。
分解与合并的开销:分治算法的效率也受到分解和合并操作的影响。如果分解和合并操作的开销较大,可能会导致算法效率下降。
空间复杂度:分治算法通常需要额外的空间来存储子问题的解,因此在空间复杂度上可能会有一定的开销。
总的来说,分治算法通过将问题划分为多个子问题,并递归地解决这些子问题,然后将子问题的解合并成原问题的解,从而高效地解决复杂的问题。它是一种重要的算法思想,被广泛应用于各个领域。
🎯注:所有完整代码:
🥏可以关注私信博主,博主可以给友友们发!💛
相关文章:

【算法设计与分析】—— 分治算法
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...
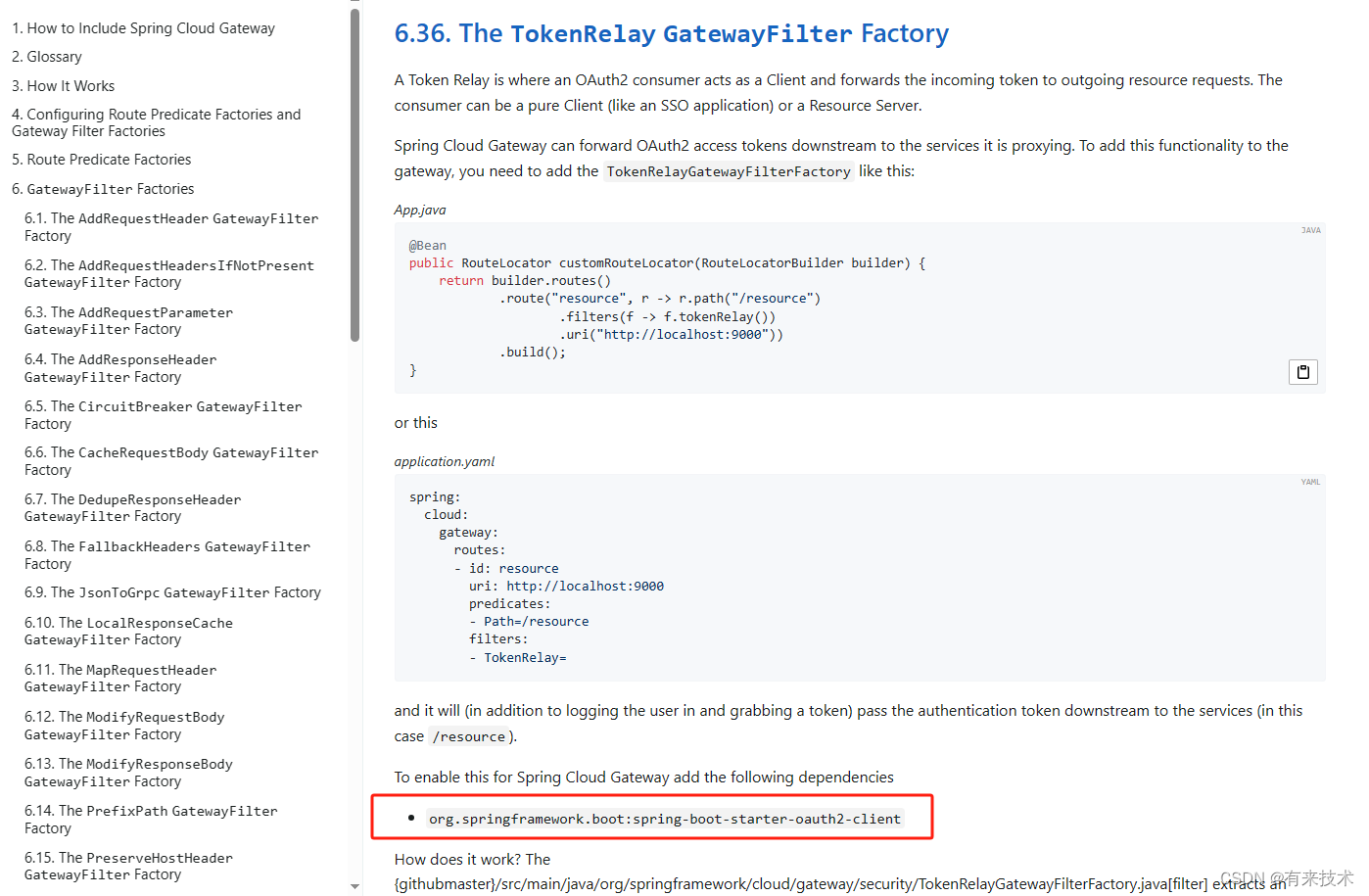
Unable to find GatewayFilterFactory with name TokenRelay
目录 问题分析解决方案参考文档开源项目微服务商城项目前后端分离项目 问题分析 Spring Cloud Gateway 网关作为代理资源服务器,需要将 JWT 传递给下游资源服务器,下面是网关的配置 spring:cloud:gateway:discovery:locator:enabled: true # 启用服务发…...
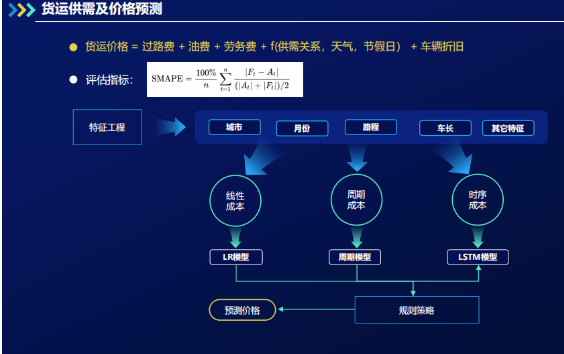
竞赛 深度学习大数据物流平台 python
文章目录 0 前言1 课题背景2 物流大数据平台的架构与设计3 智能车货匹配推荐算法的实现**1\. 问题陈述****2\. 算法模型**3\. 模型构建总览 **4 司机标签体系的搭建及算法****1\. 冷启动**2\. LSTM多标签模型算法 5 货运价格预测6 总结7 部分核心代码8 最后 0 前言 ǵ…...

git基础及原理相关解析
git入门 结构基本操作help提交分支git merge和git rebase对比 拉取 git文档 结构 工作区:电脑目录中能看到的文件暂存区:使用git add *操作提交文件的位置,一般位于.git\index,这个文件里面存储了当前位于暂存区的所有文件的校验…...

【Python机器学习】零基础掌握isotonic_regression等渗回归
遇到了数据不一致的困扰吗? 在市场分析、医疗研究或者其他数据密集型领域,经常会遇到一个问题:如何从一组不完全一致或者有噪音的数据中提取出有用的信息?例如,假设一家餐厅想要根据顾客的评分和消费金额来调整菜单。 顾客评分消费金额(元)顾客年龄访问次数4.21002533.…...

支持宏的文本编辑器提高生产力
场景 我们知道很多文本/代码编辑器支持宏的录制、重放、保存,甚至可以与快捷键命令结合的功能,快速实现重放宏的操作。 如果您的编辑器支持宏这项功能,请多使用 😃 宏化自动步骤相当于对编辑器的自动化编程,宏录制可…...
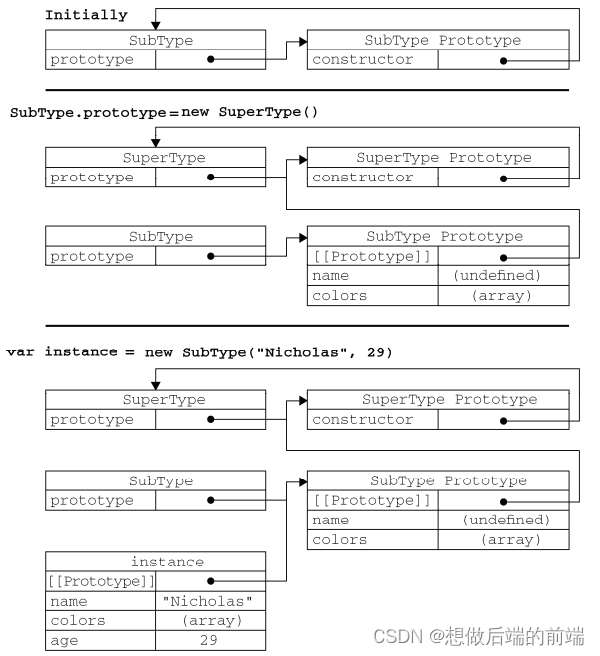
JS中面向对象的程序设计
面向对象(Object-Oriented,OO)的语言有一个标志,那就是它们都有类的概念,而通过类可以创建任意多个具有相同属性和方法的对象。但在ECMAScript 中没有类的概念,因此它的对象也与基于类的语言中的对象有所不…...
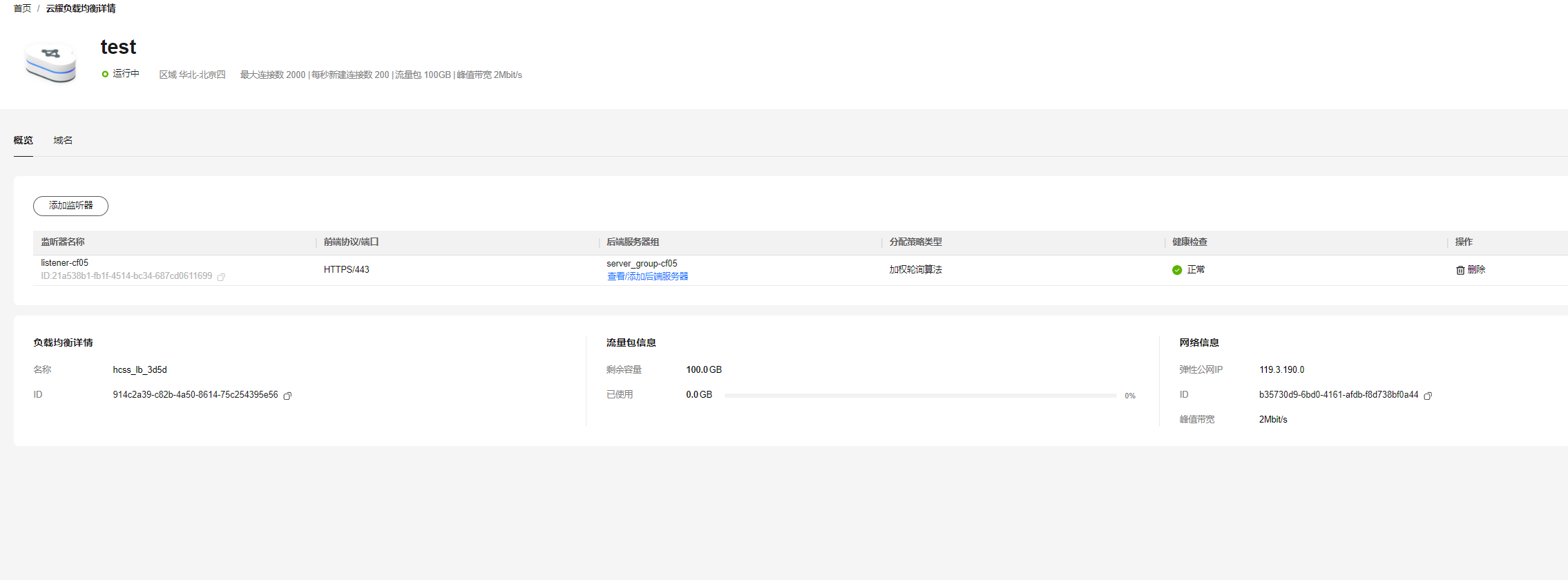
云耀服务器L实例搭配负载均衡部署Linux 可视化宝塔面板
云耀服务器L实例搭配负载均衡部署Linux 可视化宝塔面板 1. 华为云云耀服务器L实例介绍 华为云云耀服务器L实例是一种高性能、高可靠性的云服务器实例,适用于大规模企业级应用、大数据分析等场景。它基于华为最新一代的硬件虚拟化技术,提供了更高的计算…...

mac pycharm配置autopep8
mac终端安装autopep8 pip install autopep8pycharm配置autopep8 在Pycharm中点击 File–Settings—Tools–External Tools, 点击图中绿色加号图标添加扩展工具,填写相关参数配置。 Name:Autopep8(可以随便取) Tools setting&…...
Vue $nextTick
我们用一个例子来说明$nextTick的作用: 我们用一个变量showIpt来控制input框的显示和隐藏,默认是隐藏。 我们点击一个按钮后显示这个输入框的同时,input还要自动获取焦点。 但是我们点击按钮过后并没有生效。 为什么?this.show…...

linux配置dns
服务器有网,ping IP 地址可以ping的通,但是ping网站域名ping不通,需要配置dns 使用公共dns服务器 1、设置dns服务器地址 vi /etc/resolv.conf 将谷歌的dns服务器地址添加到dns解析配置中 nameserver 8.8.8.8 nameserver 8.8.4.4 保存后&…...

12 原子性|可见性|有序性|JMM内存模型
1 并发三大特性 1.1 原子性 一个或多个操作,要么全部执行,要么全部不执行。Java中,对基本数据类型的变量的读取和赋值操作是原子性操作,但不采取任何原子性保障措施的自增操作不是原子性的,如:i public c…...
)
pytorch代码复现1(基础知识)
创建矩阵 全零矩阵 In [4]: import torch torch.__version__ xtorch.empty(5,3) xOut[4]: tensor([[0.0000e00, 0.0000e00, 4.6430e-23],[1.4013e-45, 1.2612e-44, 0.0000e00],[3.5733e-43, 0.0000e00, 0.0000e00],[0.0000e00, 0.0000e00, 0.0000e00],[0.0000e00, 0.0000e00, 0…...

PostGreSQL模式schema
问题引入 之前在做数据库设计时,经常会忽略schema模式,直接在数据库下的public模式下建立各类数据表。如果数据表命名不够规范,后期寻找某张表时就会比较麻烦。通过 所幸,PostgreSQL 的模式schema管理,可以对这个问题…...
大厂面试题-什么是JVM
JVM全称是Java虚拟机,在聊什么是JVM之前,我们不妨看⼀下这张图。 从这张图中可以看出JVM所处的位置,同时也能看出它两个作用: 1、运⾏并管理Java源码⽂件所⽣成的Class⽂件, 2、在不同的操作系统上安装不同的JVM&#…...

rest参数
Rest参数是ES6中新增的一个语法特性,也称为剩余参数。其语法形式为三个点(...)加上一个名称,用于表示函数的参数个数不确定,可以将多余的参数收集到一个数组中。Rest参数只能作为最后一个参数出现,且一个函…...
Hadoop3.0大数据处理学习3(MapReduce原理分析、日志归集、序列化机制、Yarn资源调度器)
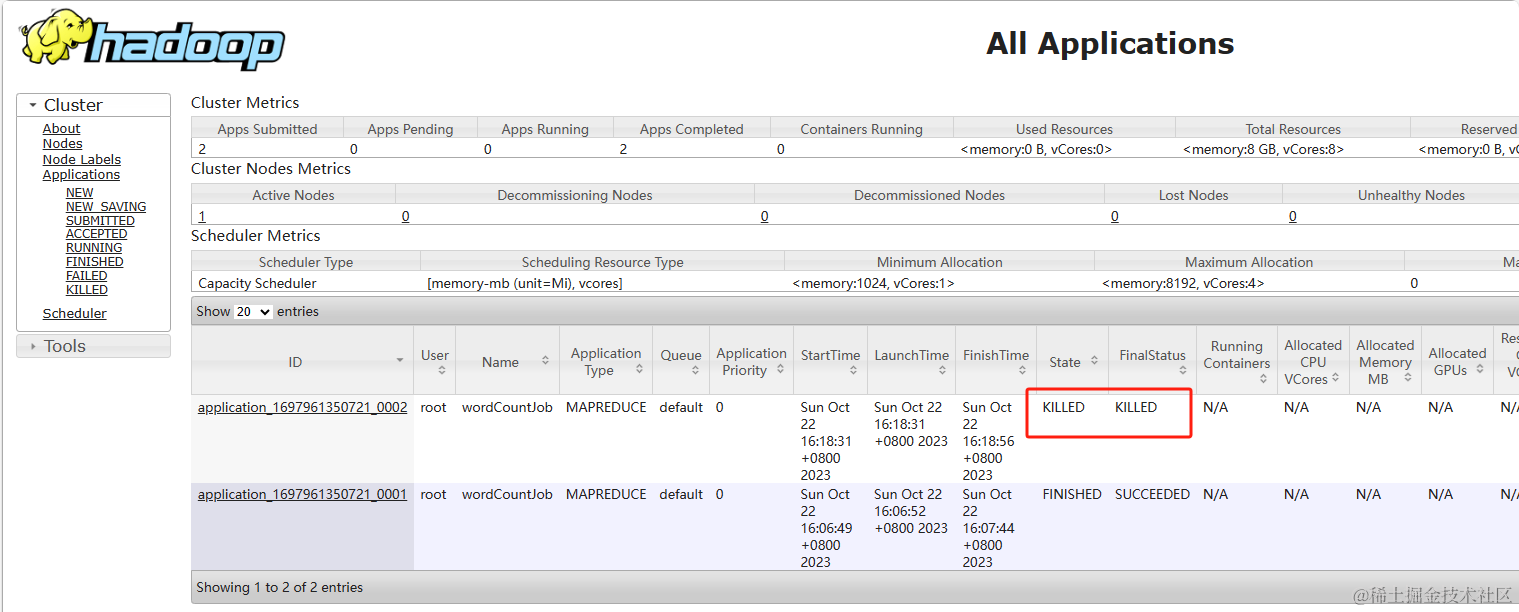
MapReduce原理分析 什么是MapReduce 前言:如果想知道一堆牌中有多少张红桃,直接的方式是一张张的检查,并数出有多少张红桃。 而MapReduce的方法是,给所有的节点分配这堆牌,让每个节点计算自己手中有几张是红桃&#…...

JS DataTable中导出PDF中文乱码
JS DataTable中导出PDF中文乱码 文章目录 JS DataTable中导出PDF中文乱码一. 问题二. 原因三. vfs_fonts.js四. pdfmake.js五. 解决六.参考资料 一. 问题 二. 原因 DataTable使用pdfmake,pdfmake默认字体为Roboto,不支持中文字体。添加自己的字体&#…...
代码签名证书续费
代码签名证书的有效周期是1-3年,这种情况下证书到期了就要重新申请办理,最开始同样的申请验证步骤还要再走一遍,尤其是Ukey还是要CA机构重新颁发,还是要等待快递配送。OV代码签名证书、EV代码签名证书目前行业内统一采取Ukey存储&…...
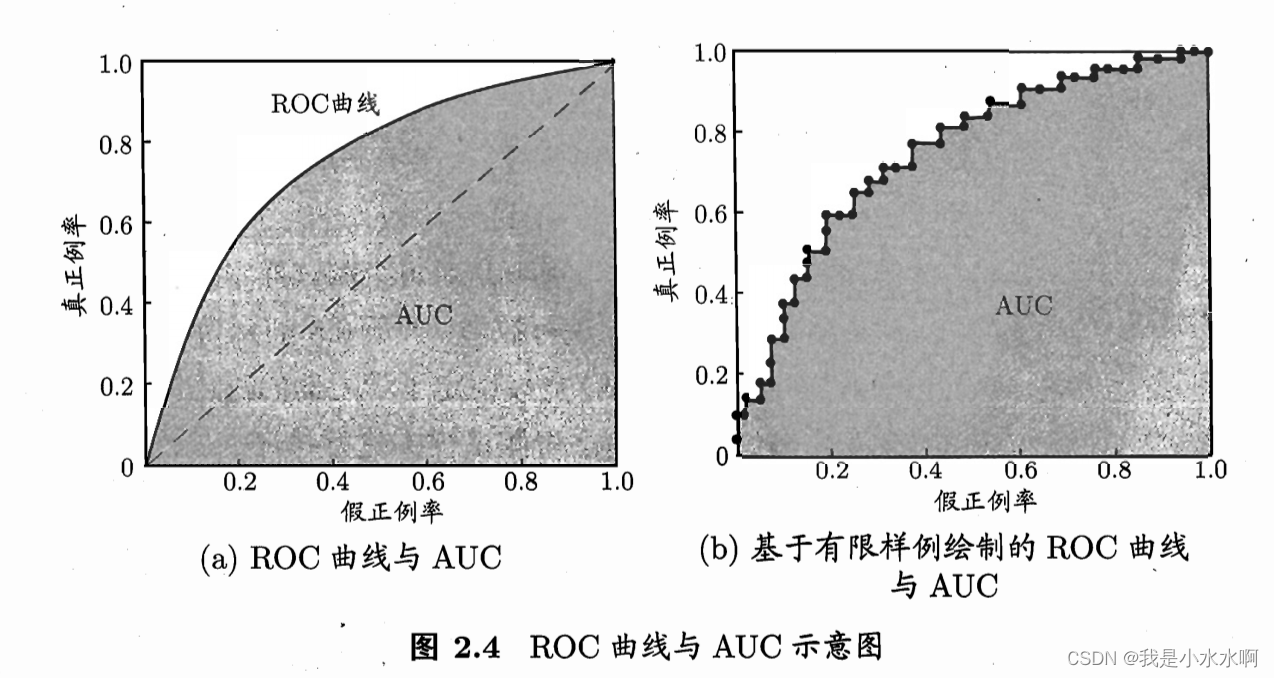
机器学习之ROC与AUC
文章目录 定义ROC曲线:AUC(Area Under the ROC Curve): 定义 ROC(Receiver Operating Characteristic)曲线和AUC(Area Under the ROC Curve)是用于评估二分类模型性能的重要工具。 …...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
